2021-2022学年八年级数学人教版上册 第十一章三角形 11.2.1三角形的外角 练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册 第十一章三角形 11.2.1三角形的外角 练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 266.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 08:54:31 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学上册
第十一章三角形
11.2.1三角形的外角
练习题
一、选择题
1.如图,在中,,将沿直线折叠,点C落在点D的位置,则的度数是(
).
A.
B.
C.
D.无法确定
2.如图,,,,则的度数是(
)
A.
B.
C.
D.
3.已知直线,一块含角的直角三角板如图所示放置,,则(
)
A.
B.
C.
D.
4.如图,直角三角形ABC的顶点A在直线m上,分别度量:①∠1,∠2,∠C;②∠2,∠3,∠B;③∠3,∠4,∠C;④∠1,∠2,∠3,可判断直线m与直线n是否平行的是(
)
A.①
B.②
C.③
D.④
5.将一副三角板按如图所示摆放,直角三角尺的锐角顶点与另一三角尺的直角顶点重合在一起,(其中,),直角边与交于点,若,则的度数为(
).
A.
B.
C.
D.
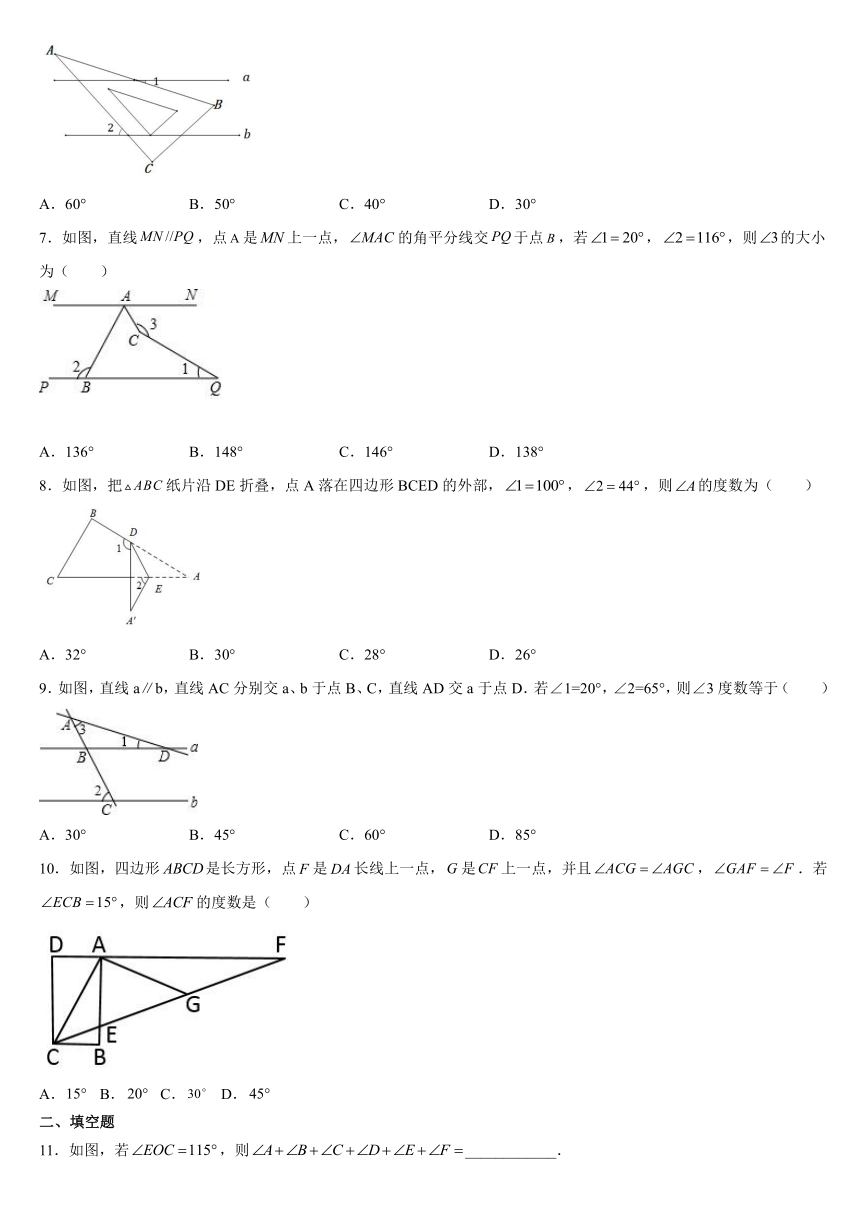
6.如图,将含30°角的直角三角板ABC放在平行线α和b上,∠C=90°,∠A=30°,若∠1=20°,则∠2的度数等于( )
A.60°
B.50°
C.40°
D.30°
7.如图,直线,点是上一点,的角平分线交于点,若,,则的大小为(
)
A.136°
B.148°
C.146°
D.138°
8.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为(
)
A.32°
B.30°
C.28°
D.26°
9.如图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D.若∠1=20°,∠2=65°,则∠3度数等于( )
A.30°
B.45°
C.60°
D.85°
10.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是(
)
A.
B.
C.
D.
二、填空题
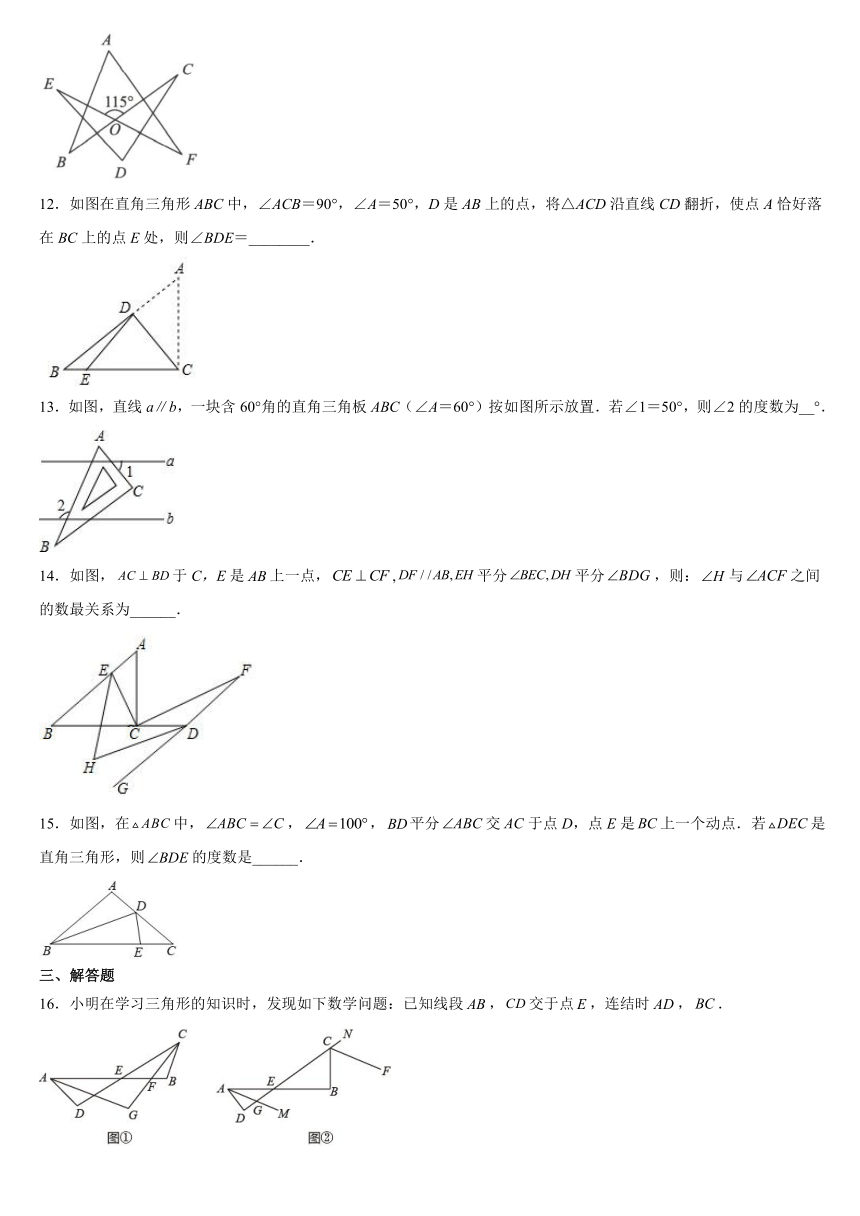
11.如图,若,则____________.
12.如图在直角三角形ABC中,∠ACB=90°,∠A=50°,D是AB上的点,将△ACD沿直线CD翻折,使点A恰好落在BC上的点E处,则∠BDE=________.
13.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为__°.
14.如图,于C,E是上一点,,平分平分,则:与之间的数最关系为______.
15.如图,在中,,,平分交于点D,点E是上一个动点.若是直角三角形,则的度数是______.
三、解答题
16.小明在学习三角形的知识时,发现如下数学问题:已知线段,交于点,连结时,.
(1)如图①,若,的平分线与的平分线交于点,求的度数;
(2)如图②,若,平分,平分,请判断与的位置关系,并说明理由.
17.如图,在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F.
(1)若∠A=62°,∠ACD=36°,∠ABE=20°,则∠BFD的度数为
°;
(2)若∠ADF+∠AEF=180°,∠FBC=∠FCB,试判断∠A与∠FBC之间的数量关系,并说明理由.
18.如图,CD是△ABC的角平分线,DE∥BC,交AC于点E.
(1)若∠A=45°,∠BDC=70°,求∠CED的度数;
(2)若∠A-∠ACD=34°,∠EDB=97°,求∠A的度数.
19.已知AM∥BN,BD平分∠ABN交AM于点D,E为射线BA上的点,设∠ABD=α.
(1)如图1,求∠ADB的度数(用α表示);
(2)如图2,若F为AD上的点,∠EFD的平分线所在直线分别交BD、ED于点G、H,当HG//BE时,求∠BEF的度数(用α表示).
20.(问题背景)∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(问题思考)(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=
.
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D=
°.
②随着点A、B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由;
(问题拓展)(3)在图②的基础上,如果∠MON=a,其余条件不变,随着点A、B的运动(如图③),∠D=
.(用含a的代数式表示)
21.已知中,是的角平分线,,.
(1)如图①,若于点,求的度数;
(2)如图②,若为上一个动点(不与,重合),且于点时,则_____;
(3)探究:如图②,中,已知,均为锐角,,是的角平分线,若为线段上一个动点(不与重合),且于点时,请写出与,的关系,并说明理由.
22.(问题情境):如图//,,,求的度数.
小明的思路是:过作//,通过平行线性质来求.
(1)按小明的思路,求的度数;
(2)(问题迁移):如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)(问题应用):在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
23.(1)已知AB∥CD,E是AB、CD间一点,如图1,给它取名“M型”;有结论:;如图2,给它取名“铅笔头型”,有结论:;
①在图3
“M型”中,AF、CF分别平分∠A、∠C,则∠F与∠E的关系是
;
②在图4
“铅笔头型”中,延长EC到G,AF、CF分别平分∠A、∠DCG,则∠F与∠E的关系是
;
(2)若直线AB与直线CD不平行,连接EG,且EG同时平分∠BEF和∠FGD.
①如图5,请探究∠1、∠2、∠F之间的数量关系?并说明理由;
②如图6,∠1比∠2的3倍多18°,∠2是∠F的,求∠F的度数.
【参考答案】
1.B
2.C
3.C
4.B
5.D
6.B
7.B
8.C
9.B
10.C
11.230°
12.10°
13.110
14.2∠H+∠ACF=180°
15.30°或70°.
16.(1)100°;(2)平行
17.(1)62;(2)∠A=2∠FBC
18.(1)130°;(2)55°
19.(1)∠ADB=α;(2)∠BEF
=2α
20.(1)135°;(2)①45;②∠D的度数不随着点A、B的运动而发生变化;∠D=45°;(3).
21.(1);(2)18°;(3).
22.(1)100゜;(2)∠APC=α+β;(3)当P点在线段OB上运动时,β-α;当P点在射线DM上运动时,α-β
23.(1)①;②
;(2)①
;②
第十一章三角形
11.2.1三角形的外角
练习题
一、选择题
1.如图,在中,,将沿直线折叠,点C落在点D的位置,则的度数是(
).
A.
B.
C.
D.无法确定
2.如图,,,,则的度数是(
)
A.
B.
C.
D.
3.已知直线,一块含角的直角三角板如图所示放置,,则(
)
A.
B.
C.
D.
4.如图,直角三角形ABC的顶点A在直线m上,分别度量:①∠1,∠2,∠C;②∠2,∠3,∠B;③∠3,∠4,∠C;④∠1,∠2,∠3,可判断直线m与直线n是否平行的是(
)
A.①
B.②
C.③
D.④
5.将一副三角板按如图所示摆放,直角三角尺的锐角顶点与另一三角尺的直角顶点重合在一起,(其中,),直角边与交于点,若,则的度数为(
).
A.
B.
C.
D.
6.如图,将含30°角的直角三角板ABC放在平行线α和b上,∠C=90°,∠A=30°,若∠1=20°,则∠2的度数等于( )
A.60°
B.50°
C.40°
D.30°
7.如图,直线,点是上一点,的角平分线交于点,若,,则的大小为(
)
A.136°
B.148°
C.146°
D.138°
8.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为(
)
A.32°
B.30°
C.28°
D.26°
9.如图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D.若∠1=20°,∠2=65°,则∠3度数等于( )
A.30°
B.45°
C.60°
D.85°
10.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是(
)
A.
B.
C.
D.
二、填空题
11.如图,若,则____________.
12.如图在直角三角形ABC中,∠ACB=90°,∠A=50°,D是AB上的点,将△ACD沿直线CD翻折,使点A恰好落在BC上的点E处,则∠BDE=________.
13.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为__°.
14.如图,于C,E是上一点,,平分平分,则:与之间的数最关系为______.
15.如图,在中,,,平分交于点D,点E是上一个动点.若是直角三角形,则的度数是______.
三、解答题
16.小明在学习三角形的知识时,发现如下数学问题:已知线段,交于点,连结时,.
(1)如图①,若,的平分线与的平分线交于点,求的度数;
(2)如图②,若,平分,平分,请判断与的位置关系,并说明理由.
17.如图,在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F.
(1)若∠A=62°,∠ACD=36°,∠ABE=20°,则∠BFD的度数为
°;
(2)若∠ADF+∠AEF=180°,∠FBC=∠FCB,试判断∠A与∠FBC之间的数量关系,并说明理由.
18.如图,CD是△ABC的角平分线,DE∥BC,交AC于点E.
(1)若∠A=45°,∠BDC=70°,求∠CED的度数;
(2)若∠A-∠ACD=34°,∠EDB=97°,求∠A的度数.
19.已知AM∥BN,BD平分∠ABN交AM于点D,E为射线BA上的点,设∠ABD=α.
(1)如图1,求∠ADB的度数(用α表示);
(2)如图2,若F为AD上的点,∠EFD的平分线所在直线分别交BD、ED于点G、H,当HG//BE时,求∠BEF的度数(用α表示).
20.(问题背景)∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(问题思考)(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=
.
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D=
°.
②随着点A、B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由;
(问题拓展)(3)在图②的基础上,如果∠MON=a,其余条件不变,随着点A、B的运动(如图③),∠D=
.(用含a的代数式表示)
21.已知中,是的角平分线,,.
(1)如图①,若于点,求的度数;
(2)如图②,若为上一个动点(不与,重合),且于点时,则_____;
(3)探究:如图②,中,已知,均为锐角,,是的角平分线,若为线段上一个动点(不与重合),且于点时,请写出与,的关系,并说明理由.
22.(问题情境):如图//,,,求的度数.
小明的思路是:过作//,通过平行线性质来求.
(1)按小明的思路,求的度数;
(2)(问题迁移):如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)(问题应用):在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
23.(1)已知AB∥CD,E是AB、CD间一点,如图1,给它取名“M型”;有结论:;如图2,给它取名“铅笔头型”,有结论:;
①在图3
“M型”中,AF、CF分别平分∠A、∠C,则∠F与∠E的关系是
;
②在图4
“铅笔头型”中,延长EC到G,AF、CF分别平分∠A、∠DCG,则∠F与∠E的关系是
;
(2)若直线AB与直线CD不平行,连接EG,且EG同时平分∠BEF和∠FGD.
①如图5,请探究∠1、∠2、∠F之间的数量关系?并说明理由;
②如图6,∠1比∠2的3倍多18°,∠2是∠F的,求∠F的度数.
【参考答案】
1.B
2.C
3.C
4.B
5.D
6.B
7.B
8.C
9.B
10.C
11.230°
12.10°
13.110
14.2∠H+∠ACF=180°
15.30°或70°.
16.(1)100°;(2)平行
17.(1)62;(2)∠A=2∠FBC
18.(1)130°;(2)55°
19.(1)∠ADB=α;(2)∠BEF
=2α
20.(1)135°;(2)①45;②∠D的度数不随着点A、B的运动而发生变化;∠D=45°;(3).
21.(1);(2)18°;(3).
22.(1)100゜;(2)∠APC=α+β;(3)当P点在线段OB上运动时,β-α;当P点在射线DM上运动时,α-β
23.(1)①;②
;(2)①
;②
