2020-2021学年高一下学期数学人教B版(2019)必修第四册第十一章立体几何初步单元测试卷(Word含答案解析)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教B版(2019)必修第四册第十一章立体几何初步单元测试卷(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 16:07:13 | ||
图片预览




文档简介
人教B版(2019)必修第四册《第十一章
立体几何初步》2021年单元测试卷
一.选择题(共8小题,满分40分,每小题5分)
1.如图是一个正方体的平面展开图,则在原正方体中,AB与CD所成的角为( )
A.
B.
C.
D.
2.在三棱锥P﹣ABC中,PA⊥平面ABC,,且三棱锥P﹣ABC的体积为,若三棱锥P﹣ABC的四个顶点都在同一球面上,则该球的表面积为( )
A.4π
B.
C.8π
D.16π
3.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:
①若a∥γ,b∥a,则b∥γ;②若a⊥b,b⊥c,则a⊥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,a⊥b,则b∥γ.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
4.已知四棱锥P﹣ABCD,底面ABCD为矩形,点P在平面ABCD上的射影为AD的中点O.若AB=2,AD=6,PO=4,则四棱锥P﹣ABCD的表面积等于( )
A.34+6
B.
C.6+64
D.6+64
5.在四面体ABCD中,若AB=CD,AC=BD=2,AD=BC,则四面体ABCD的外接球的表面积为( )
A.2π
B.4π
C.6π
D.8π
6.区块链作为一种革新的技术,已经被应用于许多领域,包括金融、政务服务、供应链、版权和专利、能源、物联网等.在区块链技术中,若密码的长度设定为256比特,则密码一共有2256种可能,因此,为了破解密码,最坏情况需要进行2256次哈希运算.现在有一台机器,每秒能进行2.5×1011次哈希运算,假设机器一直正常运转,那么在最坏情况下,这台机器破译密码所需时间大约为( )(参考数据lg2≈0.3010,lg3≈0.477)
A.4.5×1073秒
B.4.5×1065秒
C.4.5×107秒
D.28秒
7.已知如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,过A1B且与AC1平行的平面交B1C1于点P,则PC1=( )
A.2
B.
C.
D.1
8.已知平面α和α外的一条直线l,下列说法不正确的是( )
A.若l垂直于α内的两条平行线,则l⊥α
B.若l平行于α内的一条直线,则l∥α
C.若l垂直于α内的两条相交直线,则l⊥α
D.若l平行于α内的无数条直线,则l∥α
二.多选题(共4小题,满分20分,每小题5分)
9.如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面SAD∩平面SBC=l.以下四个结论中正确的是
( )
A.AD∥平面SBC
B.l∥AD
C.若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积
D.l与平面SCD所成的角为45°
10.如图,正方体ABCD﹣A1B1C1D1的棱长为a,点M,N,P分别是平面ADD1A1、平面CDD1C1、平面ABCD的中心,点Q是线段A1C1上的动点,则下列结论正确的是( )
A.PN与A1C1所成角为
B.D点到平面MNP的距离为a
C.三棱锥M﹣NPQ的体积为定值a3
D.直线DQ与平面A1ACC1所成角的正切值的最大值为
11.如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.直线AP∥平面A1C1D
C.三棱锥P﹣A1C1D的体积为定值
D.异面直线AP与A1D所成角的取值范围是[,]
12.在三棱锥A﹣BCD中,△ABC,△BCD都是边长为的正三角形,AD=a(0<a<6),M是棱AC的中点,则在a的变化过程中,下列说法正确的是( )
A.直线AD与直线BC所成的角都为
B.当时,三棱锥A﹣BCD的体积取得最大值
C.当时,三棱锥A﹣BCD的外接球的表面积为28π
D.存在某个实数a,使得∠MBD=90°
三.填空题(共4小题,满分20分,每小题5分)
13.正方体外接球的表面积为16π,则该正方体的表面积为
.
14.已知三棱锥P﹣ABC的底面ABC是边长为6的等边三角形,PA=PB=PC,先在三棱锥P﹣ABC内放入一个内切球O1,然后再放入一个球O2,使得球O2与球O1及三棱锥P﹣ABC的三个侧面都相切,则球O1的体积为
,球O2的表面积为
.
15.在直角三角形ABC中,AC=1,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则BC边长的最大值为
.
16.四棱锥P﹣ABCD的顶点都在同一球面上,若该棱锥底面为正方形,且AB=2,PA⊥面ABCD,PA=4,则该球的体积与四棱锥体积之比为
.
四.解答题(共6小题,满分70分)
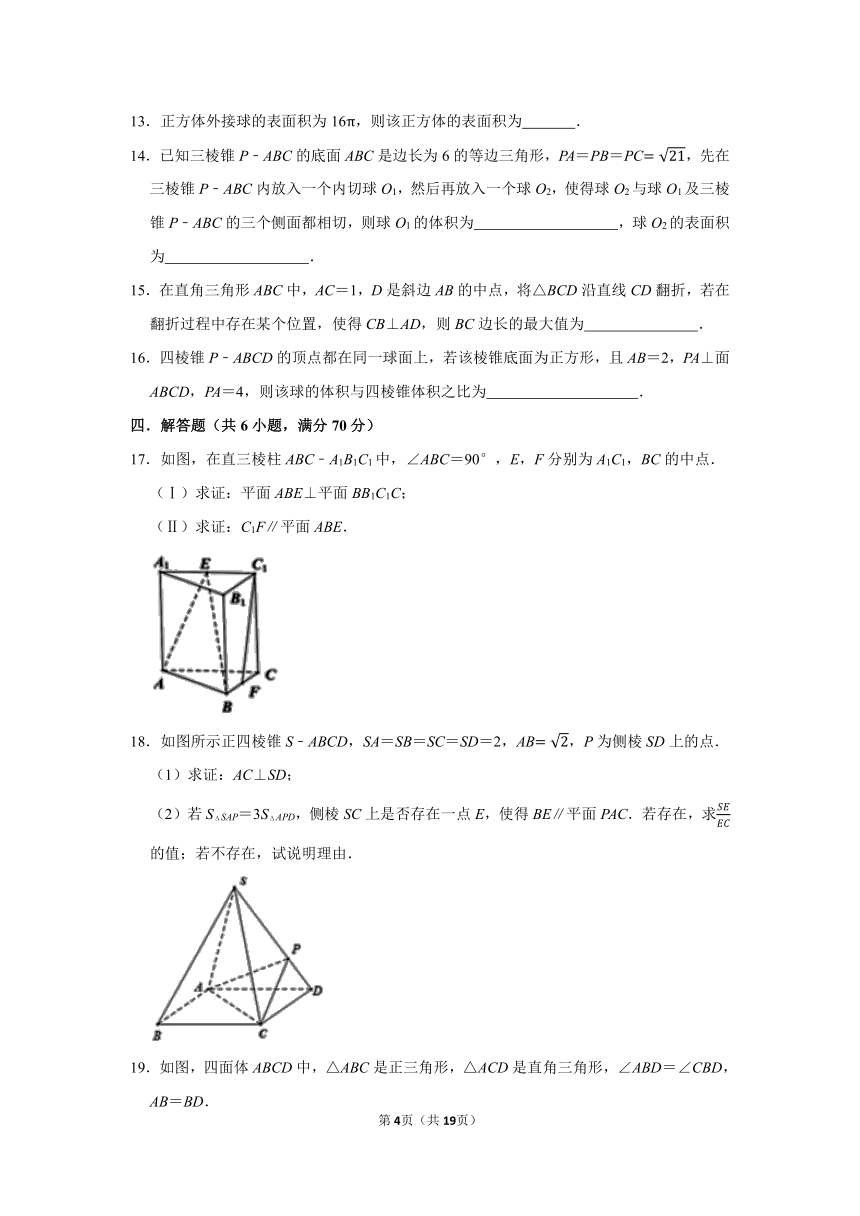
17.如图,在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E,F分别为A1C1,BC的中点.
(Ⅰ)求证:平面ABE⊥平面BB1C1C;
(Ⅱ)求证:C1F∥平面ABE.
18.如图所示正四棱锥S﹣ABCD,SA=SB=SC=SD=2,AB,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SΔSAP=3SΔAPD,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求的值;若不存在,试说明理由.
19.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)设AB长为1,点E为BD的中点,求点D到平面ACE的距离.
20.已知正四棱锥P﹣ABCD的全面积为2,记正四棱锥的高为h.
(1)试用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当V取最大值时,求异面直线AB和PD所成角的正切值.
21.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,PA=BC=AB=2,∠ABC,D、E、F分别为AC、PA、PB的中点.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)求三棱锥C﹣DEF的体积.
22.随着炎炎夏日的高温攀升和国内疫情的稳定好转,大家逐渐开始不满于口罩的“束缚”,街头巷尾,不戴口罩的人越来越多.不戴口罩固然能让人“呼吸顺畅”倍感轻松,但是戴口罩,对于新冠肺炎、流感、肺结核等呼吸道传染病具有很好的预防作用,既保护了自己,又有益于公众健康.尤其在新冠肺炎疫情防控工作中,口罩发挥了重要的作用.下面是2020年8月1日口罩市场的价格表(单位:元):
型号
价格
厂家
一次性普通口罩
一次性医用口罩
民用KN95口罩
医用KN95口罩
A
0.31
0.86
1.98
9.38
B
0.55
0.72
1.84
9.05
C
0.39
0.76
2.71
8.31
(1)根据A、B、C三个厂家的数据,分别求一次性普通口罩、一次性医用口罩、民用KN95口罩、医用KN95口罩的平均价格(结果保留三位小数);
(2)若某药店要进一批口罩销售,这四种型号的口罩各进货1000只,一次性普通口罩以1元钱销售,一次性医用口罩以2元钱销售,民用KN95口罩以3元钱销售,医用KN95口罩以10元钱销售,若这批口罩将全部出售,请问该药店在哪一个厂家进货利润更大(四种类型的口罩都在同一厂家进货)?
人教B版(2019)必修第四册《第十一章
立体几何初步》2021年单元测试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.解:由题意可知正方体的直观图如图:
连接AE,EB,则AE∥CD,
所以∠EAB就是AB与CD所成的角,因为几何体是正方体,所以△AEB是正三角形,
所以AB与CD所成的角为:.
故选:C.
2.解:∵三棱锥P﹣ABC的体积为,
∴PA,
∴PA,
将三棱锥补成三棱柱,可得球心在三棱柱的中心,
球心到底面的距离d等于三棱柱的高PA的一半,
∵△ABC是边长为2的正三角形,
∴△ABC外接圆的半径r,
∴球的半径为2,
∴球O的表面积为4π×22=16π.
故选:D.
3.解:若a∥γ,b∥a,则b∥γ或b?γ,所以①不正确;
若三条直线在同一平面内,则a∥c,
若三条直线不在同一平面内,则a,c的位置关系不确定,所以②不正确;
a与b有可能平行,也有可能异面或相交,所以③不正确;
若a⊥γ,a⊥b,则b∥γ或b?γ,所以④不正确.
故选:A.
4.解:因为点P在平面ABCD上的射影为AD的中点O,
所以PO⊥平面ABCD,CD?平面ABCD,所以CD⊥PO,
又底面ABCD为矩形,所以CD⊥AD,AD∩PO=O,
所以CD⊥平面PAD,又PD?平面PAD,
所以PD⊥CD,故△PDC为直角三角形,
在Rt△PDC中,CD=AB=2,PD,
所以,,
S矩形ABCD=AB?AD=2×6=12,
连结OC,取BC的中点E,连结PE,
因为,,
由题意可知,PB=PB,则PE⊥BC,且,
所以,
所以四棱锥P﹣ABCD的表面积为2S△PDC+S△PAD+S△PBC+S矩形ABCD
.
故选:A.
5.解:如下图所示,
将四面体ABCD放在长方体AEBF﹣GCHD内,设该长方体的长、宽、高分别为x、y、z,
则长方体的体对角线长即为长方体的外接球直径,设该长方体的外接球半径为R,
由勾股定理得,
上述三个等式全加得2(x2+y2+z2)=12,
所以,该四面体的外接球直径为,
因此,四面体ABCD的外接球的表面积为4πR2=π×(2R)2=6π,
故选:C.
6.解:设这台机器破译密码所需时间大约为x秒,
则:x?2.5×1011=2256,
两边同时取常用对数得:lg(x?2.5×1011)=lg2256,
∴lgx+lg2.5+lg1011=256lg2,
∴lgx+lg5﹣lg2+11=256lg2,
∴lgx+1﹣lg2﹣lg2+11=256lg2,
∴lgx=258lg2﹣12≈258×0.301﹣12=65.658,
∴x≈1065.658=1065×100.658,
而lg4.5=lg2lg3﹣lg2≈0.653,∴100.658≈4.5,
∴x≈4.5×1065,
故选:B.
7.解:连接AB1,交BA1于E,取B1C1的中点为P,因为E是AB1D的中点,所以EP∥AC1,
所以PC1=1.
故选:D.
8.解:若l垂直于α内的两条相交直线,则l⊥α,故A错误,C正确;
由直线与平面平行的判定可知,若平面α外的直线l平行于α内的一条直线,则l∥α,故B正确;
若平面α外的直线l平行于α内的无数条直线,也符合直线与平面平行的判定,则l∥α,故D正确.
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.解:已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面SAD∩平面SBC=l,
所以ABCD是正方形.所以AD∥BC,BC?平面SBC,所以AD∥平面SBC;A正确;
因为l,AD?平面SAD,l,BC?平面SBC,AD∥平面SBC,所以l∥AD;B正确;
若E是底面圆周上的动点,当∠ASB≤90°时,则△SAE的最大面积等于△SAB的面积;当∠ASB>90°时,△SAE的最大面积等于两条母线的夹角为90°的截面三角形的面积,所以C不正确;
因为l∥AD,l与平面SCD所成的角就是AD与平面所成角,就是∠ADB=45°.所以D正确;
故选:ABD.
10.解:对于A,连结C1D,NP,BD,A1B,
因为N,P分别是C1D和BD的中点,则NP∥C1B,
所以PN与A1C1所成的角即为C1B与A1C1所成的角,即∠A1C1B,
又A1C1=BC1=A1B,则∠A1C1B,故选项A正确;
对于B,NP,同理可得MN=MP,
则三棱锥D﹣MNP为棱长为的正四面体,
故点D到平面MNP的距离为,故选项B正确;
对于C,因为MN∥AC,AC∥A1C1,则MN∥A1C1,
又A1C1?平面MNP,MN?平面MNP,即A1C1∥平面MNP,
又点Q是线段A1C1上的动点,
则点Q到平面MNP的距离为定值,且与点A1到平面MNP的距离相等,
又M为A1D的中点,则点A1到平面MNP的距离与点D到平面MNP的距离相等,均为,
故三棱锥M﹣NPQ的体积VM﹣NPQ=VD﹣MNP,故选项C正确;
对于D,在正方体中,可知BD⊥平面ACC1A1,
则直线DQ与平面A1ACC1所成的角即为∠DQP,
所以tan∠DQP,又DP,
则tan∠DQP取最大值,PQ要取最小值为a,
此时tan∠DQP,故选项D错误.
故选:ABC.
11.解:如图,
对于A,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,
∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,
∵A1C1∩DC1=C1,∴BD1⊥平面A1C1D,故A正确;
对于B,连接AC,由AA1∥CC1,且AA1=CC1,得四边形AB1C1C为平行四边形,
∴AC∥A1C1,又A1C1?平面A1DC1,AC?平面A1DC1,
∴AC∥平面A1DC1,同理AB1∥平面A1DC1,
又AB1∩AC=A,AB1、AC?平面AB1C,
∴平面AB1C∥平面A1DC1,而AP?平面AB1C,
∴直线AP∥平面A1C1D,故B正确;
对于C,∵A1D∥B1C,A1D?平面A1C1D,B1C?平面A1C1D,∴B1C∥平面A1C1D,
∵点P在线段B1C上运动,∴P到平面A1C1D的距离为定值,
又△A1C1D的面积是定值,∴三棱锥P﹣A1C1D的体积为定值,故C正确;
对于D,当点P与线段B1C的端点重合时,异面直线AP与A1D所成角取得最小值为,
故异面直线AP与A1D所成角的取值范围是[,],故D错误,
故选:ABC.
12.解:对于A:取BC的中点E,如图1所示:
图(1)
则AE⊥BC,DE⊥BC,
则BC⊥平面ADE,故AD⊥BC,
故选项A正确;
对于B:因为棱长为,则AE=DE=3,
故当AE⊥平面BCD时,三棱锥的A﹣BCD的体积取得最大值,则,故B错误;
对于C:当时,∠AED=120°,分别取平面ABC和平面BCD的外心O1,O2,
如图2所示:
图(2),
可求得|O1E|=|O2E|=1,|O2B|=|O2C|=|O2D|=2,
过分别作平面ABC和平面BCD的垂线交点为O,则平面图如图2,
因为∠AED=120°,则∠O1EO2=120°,则∠OEO2=60°,
则,则外接球半径R2,
故球的表面积为4πR2=28π,故C正确;
对于D:如图3所示:
图(3),
当A∈平面BCD时,A与G点重合,
故A在平面BCD的投影为GD,因为M是棱AC的中点,
故M在平面BCD的投影为M1M2,其中M1,M2分别是GC,CD的中点,
因为∠MBD=90°,则∠M'BD=90°,其中M'在M1M2上,
则M'与M1重合,此时a=6,故不成立,
则D错误;
综上所述,故选:AC.
三.填空题(共4小题,满分20分,每小题5分)
13.解:设正方体的棱长为a,则正方体的体对角线的长就是外接球的直径,
外接球的半径为:,
∵正方体外接球表面积是16
π,
∴,
解得
,
所以正方体的表面积为6a2=32,
故答案为:32.
14.解:设O为△ABC外接圆的圆心,因为ABC是边长为6的等边三角形,
所以,
因为OP2+OA2=PA2,解得OP=3,
设球O1的半径为r,球O2的半径为R,
由等体积法可得,
,
所以1,
所以球O1的体积为;
作截面图如图所示,可知O1O=O1N=1,
则PN=1,PO1=2,PO2=1﹣R,
因为△PO2E∽△PO1F,则,即,解得,
所以球O2的表面积为.
故答案为:;.
15.解:设BC=x,由题意得,AD=CD=BD,
取BC中点E,翻折前,在图1中,连接DE,CD,则DEAC,
翻折后,在图2中,此时
CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE,AD,
在△ADE中:①,②,③x>0,
由①②③,得0<x.
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1,
综上,x的取值范围为(0,],
所以BC边长的最大值为.
故答案为:.
16.解:设此球半径为R,
因底面ABCD是边长为2的正方形,且PA⊥面ABCD,若四棱锥的体积为:,
可以把四棱锥P﹣ABCD补成一个以ABCD为底、PA为侧棱的长方体,
则这个长方体的外接球就是四棱锥P﹣ABCD的外接球,球心O就是PC的中点,
∴(2R)2=42+22+22=24,∴R,
则该球的体积为.
该球的体积与四棱锥体积之比为:.
故答案为:.
四.解答题(共6小题,满分70分)
17.证明:(Ⅰ)在直三棱柱ABC﹣A1B1C1中,
∵BB1⊥平面ABC,AB?平面ABC,∴BB1⊥AB.
又∵∠ABC=90°,∴AB⊥BC.
又BB1∩BC=B,∴AB⊥平面BB1C1C,
又AB?平面ABE,∴平面ABE⊥平面BB1C1C;
(Ⅱ)取AB的中点G,连接EG、GF,如图所示.
∵G、F分别是AB、BC的中点,∴FG∥AC,且.
又∵E为A1C1的中点,∴,且AC∥A1C1.
∴GF∥EC1,且GF=EC1,
∴四边形EGFC1是平行四边形,∴C1F∥EG.
又∵C1F?平面ABE,EG?平面ABE,∴C1F∥平面ABE.
18.证明:(1)连BD,设AC交BD于O,由题意SO⊥AC.
在正方形ABCD中,有AC⊥BD,又SO∩BD=O,
∴AC⊥平面SBD,得AC⊥SD;
解:(2)在棱SC上存在一点E,使BE∥平面PAC,满足2.
证明如下:
取SD中点为N,∵SΔSAP=3SΔAPD,∴,则PN=PD,
过N作PC的平行线交SC于E,连BN,BE.
在△BDN中,有BN∥PO,
∵PO?平面PAC,BN?平面PAC,∴BN∥平面PAC,
又由于NE∥PC,
PC?平面PAC,NE?平面PAC,∴NE∥平面PAC,
∵BN∩NE=N,∴平面BEN∥平面PAC,得BE∥平面PAC,
由于,∴2.
19.(1)证明:如图所示,取AC的中点O,连接BO,OD,
∵△ABC是等边三角形,∴OB⊥AC,△ABD与△CBD中,
AB=BD=BC,∠ABD=∠CBD,
∴△ABD≌△CBD,∴AD=CD,
∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°,
∴,∴DO2+BO2=AB2=BD2,
∴∠BOD=90°,∴OB⊥OD
又DO∩AC=O,∴OB⊥平面ACD.
又OB?平面ABC,∴平面ACD⊥平面ABC.
(2)设E是BD的中点,△ABC是等边三角形,边长为1,
△ABD是等腰三角形,|AB|=|BD|=1,|AD|,
∴,
,
,
,
,
,
点D到平面ACE的距离.
20.解:(1)设正四棱锥的底面边长为a,侧面三角形的高为H,则a2+2aH=2,
∴H,又,
∴a.
∵h2(当且仅当h,即h=1时取等号).
∴,即正四棱锥体积V的最大值为(当h=1,a时取最大值);
(2)取CD的中点Q,正方形ABCD的中心为O,连接PO,PQ,OQ.
∵AB∥CD,∴∠PDQ即为异面直线AB与PD所成角.
∵Q为CD的中点,PC=PD,∴PQ⊥CD.
即PQ=H,由(1)知,H.
又DQ,∴tan.
即异面直线AB和PD所成角的正切值为3.
21.证明:(Ⅰ)∵AB=BC,AD=DC,∴BD⊥AC,
∵PA⊥底面ABC,BD?平面ABC,∴PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC,
∵PC?平面PAC,
∴BD⊥PC;
解:(Ⅱ)∵D为AC的中点,∴A、C到平面DEF的距离相等,
∴VC﹣DEF=VA﹣DEF=VD﹣AEF,
在△ABC中,∵BC=AB=2,∠ABC,∴,则AD,
∵E、F分别为PA、PB的中点,∴EF∥AB,且EFAB=1,
由PA⊥底面ABC,知PA⊥AB,∴EF⊥AE,
∴.
∵BD⊥AC,作DH⊥AB,垂足为H,则DH⊥平面PAB,
在Rt△ABD中,AB=2,AD,
∴DH.
∴.
22.解:(1)一次性普通口罩的平均价格为:元,
一次性医用口罩的平均价格为:元,
民用KN95口罩的平均价格为:元,
医用KN95口罩的平均价格为:元.
(2)在A厂家购买口罩后销售的利润为:1000×(1﹣0.31)+1000×(2﹣0.86)+1000×(3﹣1.98)+1000×(10﹣9.38)=3470元;
在B厂家购买口罩后销售的利润为:1000×(1﹣0.55)+1000×(2﹣0.72)+1000×(3﹣1.84)+1000×(10﹣9.05)=3840元;
在C厂家购买口罩后销售的利润为;1000×(1﹣0.39)+1000×(2﹣0.76)+1000×(3﹣2.71)+1000×(10﹣8.31)=3830元;
由2840>3830>3470,
故该药店在B厂家进货利润更大.
第1页(共3页)
立体几何初步》2021年单元测试卷
一.选择题(共8小题,满分40分,每小题5分)
1.如图是一个正方体的平面展开图,则在原正方体中,AB与CD所成的角为( )
A.
B.
C.
D.
2.在三棱锥P﹣ABC中,PA⊥平面ABC,,且三棱锥P﹣ABC的体积为,若三棱锥P﹣ABC的四个顶点都在同一球面上,则该球的表面积为( )
A.4π
B.
C.8π
D.16π
3.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:
①若a∥γ,b∥a,则b∥γ;②若a⊥b,b⊥c,则a⊥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,a⊥b,则b∥γ.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
4.已知四棱锥P﹣ABCD,底面ABCD为矩形,点P在平面ABCD上的射影为AD的中点O.若AB=2,AD=6,PO=4,则四棱锥P﹣ABCD的表面积等于( )
A.34+6
B.
C.6+64
D.6+64
5.在四面体ABCD中,若AB=CD,AC=BD=2,AD=BC,则四面体ABCD的外接球的表面积为( )
A.2π
B.4π
C.6π
D.8π
6.区块链作为一种革新的技术,已经被应用于许多领域,包括金融、政务服务、供应链、版权和专利、能源、物联网等.在区块链技术中,若密码的长度设定为256比特,则密码一共有2256种可能,因此,为了破解密码,最坏情况需要进行2256次哈希运算.现在有一台机器,每秒能进行2.5×1011次哈希运算,假设机器一直正常运转,那么在最坏情况下,这台机器破译密码所需时间大约为( )(参考数据lg2≈0.3010,lg3≈0.477)
A.4.5×1073秒
B.4.5×1065秒
C.4.5×107秒
D.28秒
7.已知如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,过A1B且与AC1平行的平面交B1C1于点P,则PC1=( )
A.2
B.
C.
D.1
8.已知平面α和α外的一条直线l,下列说法不正确的是( )
A.若l垂直于α内的两条平行线,则l⊥α
B.若l平行于α内的一条直线,则l∥α
C.若l垂直于α内的两条相交直线,则l⊥α
D.若l平行于α内的无数条直线,则l∥α
二.多选题(共4小题,满分20分,每小题5分)
9.如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面SAD∩平面SBC=l.以下四个结论中正确的是
( )
A.AD∥平面SBC
B.l∥AD
C.若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积
D.l与平面SCD所成的角为45°
10.如图,正方体ABCD﹣A1B1C1D1的棱长为a,点M,N,P分别是平面ADD1A1、平面CDD1C1、平面ABCD的中心,点Q是线段A1C1上的动点,则下列结论正确的是( )
A.PN与A1C1所成角为
B.D点到平面MNP的距离为a
C.三棱锥M﹣NPQ的体积为定值a3
D.直线DQ与平面A1ACC1所成角的正切值的最大值为
11.如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.直线AP∥平面A1C1D
C.三棱锥P﹣A1C1D的体积为定值
D.异面直线AP与A1D所成角的取值范围是[,]
12.在三棱锥A﹣BCD中,△ABC,△BCD都是边长为的正三角形,AD=a(0<a<6),M是棱AC的中点,则在a的变化过程中,下列说法正确的是( )
A.直线AD与直线BC所成的角都为
B.当时,三棱锥A﹣BCD的体积取得最大值
C.当时,三棱锥A﹣BCD的外接球的表面积为28π
D.存在某个实数a,使得∠MBD=90°
三.填空题(共4小题,满分20分,每小题5分)
13.正方体外接球的表面积为16π,则该正方体的表面积为
.
14.已知三棱锥P﹣ABC的底面ABC是边长为6的等边三角形,PA=PB=PC,先在三棱锥P﹣ABC内放入一个内切球O1,然后再放入一个球O2,使得球O2与球O1及三棱锥P﹣ABC的三个侧面都相切,则球O1的体积为
,球O2的表面积为
.
15.在直角三角形ABC中,AC=1,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则BC边长的最大值为
.
16.四棱锥P﹣ABCD的顶点都在同一球面上,若该棱锥底面为正方形,且AB=2,PA⊥面ABCD,PA=4,则该球的体积与四棱锥体积之比为
.
四.解答题(共6小题,满分70分)
17.如图,在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E,F分别为A1C1,BC的中点.
(Ⅰ)求证:平面ABE⊥平面BB1C1C;
(Ⅱ)求证:C1F∥平面ABE.
18.如图所示正四棱锥S﹣ABCD,SA=SB=SC=SD=2,AB,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SΔSAP=3SΔAPD,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求的值;若不存在,试说明理由.
19.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)设AB长为1,点E为BD的中点,求点D到平面ACE的距离.
20.已知正四棱锥P﹣ABCD的全面积为2,记正四棱锥的高为h.
(1)试用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当V取最大值时,求异面直线AB和PD所成角的正切值.
21.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,PA=BC=AB=2,∠ABC,D、E、F分别为AC、PA、PB的中点.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)求三棱锥C﹣DEF的体积.
22.随着炎炎夏日的高温攀升和国内疫情的稳定好转,大家逐渐开始不满于口罩的“束缚”,街头巷尾,不戴口罩的人越来越多.不戴口罩固然能让人“呼吸顺畅”倍感轻松,但是戴口罩,对于新冠肺炎、流感、肺结核等呼吸道传染病具有很好的预防作用,既保护了自己,又有益于公众健康.尤其在新冠肺炎疫情防控工作中,口罩发挥了重要的作用.下面是2020年8月1日口罩市场的价格表(单位:元):
型号
价格
厂家
一次性普通口罩
一次性医用口罩
民用KN95口罩
医用KN95口罩
A
0.31
0.86
1.98
9.38
B
0.55
0.72
1.84
9.05
C
0.39
0.76
2.71
8.31
(1)根据A、B、C三个厂家的数据,分别求一次性普通口罩、一次性医用口罩、民用KN95口罩、医用KN95口罩的平均价格(结果保留三位小数);
(2)若某药店要进一批口罩销售,这四种型号的口罩各进货1000只,一次性普通口罩以1元钱销售,一次性医用口罩以2元钱销售,民用KN95口罩以3元钱销售,医用KN95口罩以10元钱销售,若这批口罩将全部出售,请问该药店在哪一个厂家进货利润更大(四种类型的口罩都在同一厂家进货)?
人教B版(2019)必修第四册《第十一章
立体几何初步》2021年单元测试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.解:由题意可知正方体的直观图如图:
连接AE,EB,则AE∥CD,
所以∠EAB就是AB与CD所成的角,因为几何体是正方体,所以△AEB是正三角形,
所以AB与CD所成的角为:.
故选:C.
2.解:∵三棱锥P﹣ABC的体积为,
∴PA,
∴PA,
将三棱锥补成三棱柱,可得球心在三棱柱的中心,
球心到底面的距离d等于三棱柱的高PA的一半,
∵△ABC是边长为2的正三角形,
∴△ABC外接圆的半径r,
∴球的半径为2,
∴球O的表面积为4π×22=16π.
故选:D.
3.解:若a∥γ,b∥a,则b∥γ或b?γ,所以①不正确;
若三条直线在同一平面内,则a∥c,
若三条直线不在同一平面内,则a,c的位置关系不确定,所以②不正确;
a与b有可能平行,也有可能异面或相交,所以③不正确;
若a⊥γ,a⊥b,则b∥γ或b?γ,所以④不正确.
故选:A.
4.解:因为点P在平面ABCD上的射影为AD的中点O,
所以PO⊥平面ABCD,CD?平面ABCD,所以CD⊥PO,
又底面ABCD为矩形,所以CD⊥AD,AD∩PO=O,
所以CD⊥平面PAD,又PD?平面PAD,
所以PD⊥CD,故△PDC为直角三角形,
在Rt△PDC中,CD=AB=2,PD,
所以,,
S矩形ABCD=AB?AD=2×6=12,
连结OC,取BC的中点E,连结PE,
因为,,
由题意可知,PB=PB,则PE⊥BC,且,
所以,
所以四棱锥P﹣ABCD的表面积为2S△PDC+S△PAD+S△PBC+S矩形ABCD
.
故选:A.
5.解:如下图所示,
将四面体ABCD放在长方体AEBF﹣GCHD内,设该长方体的长、宽、高分别为x、y、z,
则长方体的体对角线长即为长方体的外接球直径,设该长方体的外接球半径为R,
由勾股定理得,
上述三个等式全加得2(x2+y2+z2)=12,
所以,该四面体的外接球直径为,
因此,四面体ABCD的外接球的表面积为4πR2=π×(2R)2=6π,
故选:C.
6.解:设这台机器破译密码所需时间大约为x秒,
则:x?2.5×1011=2256,
两边同时取常用对数得:lg(x?2.5×1011)=lg2256,
∴lgx+lg2.5+lg1011=256lg2,
∴lgx+lg5﹣lg2+11=256lg2,
∴lgx+1﹣lg2﹣lg2+11=256lg2,
∴lgx=258lg2﹣12≈258×0.301﹣12=65.658,
∴x≈1065.658=1065×100.658,
而lg4.5=lg2lg3﹣lg2≈0.653,∴100.658≈4.5,
∴x≈4.5×1065,
故选:B.
7.解:连接AB1,交BA1于E,取B1C1的中点为P,因为E是AB1D的中点,所以EP∥AC1,
所以PC1=1.
故选:D.
8.解:若l垂直于α内的两条相交直线,则l⊥α,故A错误,C正确;
由直线与平面平行的判定可知,若平面α外的直线l平行于α内的一条直线,则l∥α,故B正确;
若平面α外的直线l平行于α内的无数条直线,也符合直线与平面平行的判定,则l∥α,故D正确.
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.解:已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面SAD∩平面SBC=l,
所以ABCD是正方形.所以AD∥BC,BC?平面SBC,所以AD∥平面SBC;A正确;
因为l,AD?平面SAD,l,BC?平面SBC,AD∥平面SBC,所以l∥AD;B正确;
若E是底面圆周上的动点,当∠ASB≤90°时,则△SAE的最大面积等于△SAB的面积;当∠ASB>90°时,△SAE的最大面积等于两条母线的夹角为90°的截面三角形的面积,所以C不正确;
因为l∥AD,l与平面SCD所成的角就是AD与平面所成角,就是∠ADB=45°.所以D正确;
故选:ABD.
10.解:对于A,连结C1D,NP,BD,A1B,
因为N,P分别是C1D和BD的中点,则NP∥C1B,
所以PN与A1C1所成的角即为C1B与A1C1所成的角,即∠A1C1B,
又A1C1=BC1=A1B,则∠A1C1B,故选项A正确;
对于B,NP,同理可得MN=MP,
则三棱锥D﹣MNP为棱长为的正四面体,
故点D到平面MNP的距离为,故选项B正确;
对于C,因为MN∥AC,AC∥A1C1,则MN∥A1C1,
又A1C1?平面MNP,MN?平面MNP,即A1C1∥平面MNP,
又点Q是线段A1C1上的动点,
则点Q到平面MNP的距离为定值,且与点A1到平面MNP的距离相等,
又M为A1D的中点,则点A1到平面MNP的距离与点D到平面MNP的距离相等,均为,
故三棱锥M﹣NPQ的体积VM﹣NPQ=VD﹣MNP,故选项C正确;
对于D,在正方体中,可知BD⊥平面ACC1A1,
则直线DQ与平面A1ACC1所成的角即为∠DQP,
所以tan∠DQP,又DP,
则tan∠DQP取最大值,PQ要取最小值为a,
此时tan∠DQP,故选项D错误.
故选:ABC.
11.解:如图,
对于A,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,
∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,
∵A1C1∩DC1=C1,∴BD1⊥平面A1C1D,故A正确;
对于B,连接AC,由AA1∥CC1,且AA1=CC1,得四边形AB1C1C为平行四边形,
∴AC∥A1C1,又A1C1?平面A1DC1,AC?平面A1DC1,
∴AC∥平面A1DC1,同理AB1∥平面A1DC1,
又AB1∩AC=A,AB1、AC?平面AB1C,
∴平面AB1C∥平面A1DC1,而AP?平面AB1C,
∴直线AP∥平面A1C1D,故B正确;
对于C,∵A1D∥B1C,A1D?平面A1C1D,B1C?平面A1C1D,∴B1C∥平面A1C1D,
∵点P在线段B1C上运动,∴P到平面A1C1D的距离为定值,
又△A1C1D的面积是定值,∴三棱锥P﹣A1C1D的体积为定值,故C正确;
对于D,当点P与线段B1C的端点重合时,异面直线AP与A1D所成角取得最小值为,
故异面直线AP与A1D所成角的取值范围是[,],故D错误,
故选:ABC.
12.解:对于A:取BC的中点E,如图1所示:
图(1)
则AE⊥BC,DE⊥BC,
则BC⊥平面ADE,故AD⊥BC,
故选项A正确;
对于B:因为棱长为,则AE=DE=3,
故当AE⊥平面BCD时,三棱锥的A﹣BCD的体积取得最大值,则,故B错误;
对于C:当时,∠AED=120°,分别取平面ABC和平面BCD的外心O1,O2,
如图2所示:
图(2),
可求得|O1E|=|O2E|=1,|O2B|=|O2C|=|O2D|=2,
过分别作平面ABC和平面BCD的垂线交点为O,则平面图如图2,
因为∠AED=120°,则∠O1EO2=120°,则∠OEO2=60°,
则,则外接球半径R2,
故球的表面积为4πR2=28π,故C正确;
对于D:如图3所示:
图(3),
当A∈平面BCD时,A与G点重合,
故A在平面BCD的投影为GD,因为M是棱AC的中点,
故M在平面BCD的投影为M1M2,其中M1,M2分别是GC,CD的中点,
因为∠MBD=90°,则∠M'BD=90°,其中M'在M1M2上,
则M'与M1重合,此时a=6,故不成立,
则D错误;
综上所述,故选:AC.
三.填空题(共4小题,满分20分,每小题5分)
13.解:设正方体的棱长为a,则正方体的体对角线的长就是外接球的直径,
外接球的半径为:,
∵正方体外接球表面积是16
π,
∴,
解得
,
所以正方体的表面积为6a2=32,
故答案为:32.
14.解:设O为△ABC外接圆的圆心,因为ABC是边长为6的等边三角形,
所以,
因为OP2+OA2=PA2,解得OP=3,
设球O1的半径为r,球O2的半径为R,
由等体积法可得,
,
所以1,
所以球O1的体积为;
作截面图如图所示,可知O1O=O1N=1,
则PN=1,PO1=2,PO2=1﹣R,
因为△PO2E∽△PO1F,则,即,解得,
所以球O2的表面积为.
故答案为:;.
15.解:设BC=x,由题意得,AD=CD=BD,
取BC中点E,翻折前,在图1中,连接DE,CD,则DEAC,
翻折后,在图2中,此时
CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE,AD,
在△ADE中:①,②,③x>0,
由①②③,得0<x.
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1,
综上,x的取值范围为(0,],
所以BC边长的最大值为.
故答案为:.
16.解:设此球半径为R,
因底面ABCD是边长为2的正方形,且PA⊥面ABCD,若四棱锥的体积为:,
可以把四棱锥P﹣ABCD补成一个以ABCD为底、PA为侧棱的长方体,
则这个长方体的外接球就是四棱锥P﹣ABCD的外接球,球心O就是PC的中点,
∴(2R)2=42+22+22=24,∴R,
则该球的体积为.
该球的体积与四棱锥体积之比为:.
故答案为:.
四.解答题(共6小题,满分70分)
17.证明:(Ⅰ)在直三棱柱ABC﹣A1B1C1中,
∵BB1⊥平面ABC,AB?平面ABC,∴BB1⊥AB.
又∵∠ABC=90°,∴AB⊥BC.
又BB1∩BC=B,∴AB⊥平面BB1C1C,
又AB?平面ABE,∴平面ABE⊥平面BB1C1C;
(Ⅱ)取AB的中点G,连接EG、GF,如图所示.
∵G、F分别是AB、BC的中点,∴FG∥AC,且.
又∵E为A1C1的中点,∴,且AC∥A1C1.
∴GF∥EC1,且GF=EC1,
∴四边形EGFC1是平行四边形,∴C1F∥EG.
又∵C1F?平面ABE,EG?平面ABE,∴C1F∥平面ABE.
18.证明:(1)连BD,设AC交BD于O,由题意SO⊥AC.
在正方形ABCD中,有AC⊥BD,又SO∩BD=O,
∴AC⊥平面SBD,得AC⊥SD;
解:(2)在棱SC上存在一点E,使BE∥平面PAC,满足2.
证明如下:
取SD中点为N,∵SΔSAP=3SΔAPD,∴,则PN=PD,
过N作PC的平行线交SC于E,连BN,BE.
在△BDN中,有BN∥PO,
∵PO?平面PAC,BN?平面PAC,∴BN∥平面PAC,
又由于NE∥PC,
PC?平面PAC,NE?平面PAC,∴NE∥平面PAC,
∵BN∩NE=N,∴平面BEN∥平面PAC,得BE∥平面PAC,
由于,∴2.
19.(1)证明:如图所示,取AC的中点O,连接BO,OD,
∵△ABC是等边三角形,∴OB⊥AC,△ABD与△CBD中,
AB=BD=BC,∠ABD=∠CBD,
∴△ABD≌△CBD,∴AD=CD,
∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°,
∴,∴DO2+BO2=AB2=BD2,
∴∠BOD=90°,∴OB⊥OD
又DO∩AC=O,∴OB⊥平面ACD.
又OB?平面ABC,∴平面ACD⊥平面ABC.
(2)设E是BD的中点,△ABC是等边三角形,边长为1,
△ABD是等腰三角形,|AB|=|BD|=1,|AD|,
∴,
,
,
,
,
,
点D到平面ACE的距离.
20.解:(1)设正四棱锥的底面边长为a,侧面三角形的高为H,则a2+2aH=2,
∴H,又,
∴a.
∵h2(当且仅当h,即h=1时取等号).
∴,即正四棱锥体积V的最大值为(当h=1,a时取最大值);
(2)取CD的中点Q,正方形ABCD的中心为O,连接PO,PQ,OQ.
∵AB∥CD,∴∠PDQ即为异面直线AB与PD所成角.
∵Q为CD的中点,PC=PD,∴PQ⊥CD.
即PQ=H,由(1)知,H.
又DQ,∴tan.
即异面直线AB和PD所成角的正切值为3.
21.证明:(Ⅰ)∵AB=BC,AD=DC,∴BD⊥AC,
∵PA⊥底面ABC,BD?平面ABC,∴PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC,
∵PC?平面PAC,
∴BD⊥PC;
解:(Ⅱ)∵D为AC的中点,∴A、C到平面DEF的距离相等,
∴VC﹣DEF=VA﹣DEF=VD﹣AEF,
在△ABC中,∵BC=AB=2,∠ABC,∴,则AD,
∵E、F分别为PA、PB的中点,∴EF∥AB,且EFAB=1,
由PA⊥底面ABC,知PA⊥AB,∴EF⊥AE,
∴.
∵BD⊥AC,作DH⊥AB,垂足为H,则DH⊥平面PAB,
在Rt△ABD中,AB=2,AD,
∴DH.
∴.
22.解:(1)一次性普通口罩的平均价格为:元,
一次性医用口罩的平均价格为:元,
民用KN95口罩的平均价格为:元,
医用KN95口罩的平均价格为:元.
(2)在A厂家购买口罩后销售的利润为:1000×(1﹣0.31)+1000×(2﹣0.86)+1000×(3﹣1.98)+1000×(10﹣9.38)=3470元;
在B厂家购买口罩后销售的利润为:1000×(1﹣0.55)+1000×(2﹣0.72)+1000×(3﹣1.84)+1000×(10﹣9.05)=3840元;
在C厂家购买口罩后销售的利润为;1000×(1﹣0.39)+1000×(2﹣0.76)+1000×(3﹣2.71)+1000×(10﹣8.31)=3830元;
由2840>3830>3470,
故该药店在B厂家进货利润更大.
第1页(共3页)
同课章节目录
