2020-2021学年高中数学湘教版选修2-3第8章统计与概率习题B(Word含解析)
文档属性
| 名称 | 2020-2021学年高中数学湘教版选修2-3第8章统计与概率习题B(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览




文档简介
高中数学选修2-3《统计与概率》
第八单元测试卷B卷
一、选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)从某选手的9个得分中去掉1个最高分和1个最低分,7个剩余分数的平均分为91,由于现场做的9个分数的茎叶图有一个数据模糊无法辨认,在右图中以表示,则7个剩余分数的方差为(
)
A.
B.
C.36
D.
(2)A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为(
)
A.
B.
C.
D.
(3)欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为的圆面,中间有边长为
的正方形孔,现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为(
)
A.
B.
C.
D.
(4)某研究机构对儿童记忆能力和识图能力进行统计分析,得到如下数据:
记忆能力
识图能力
由表中数据,求得线性回归方程为,由此估计某儿童的记忆能力为时,则他的识图能力为(
)
A.9.2
B.9.5
C.9.8
D.10
(5)
某中学组织了“自主招生数学选拔赛”,已知此次选拔赛的数学成绩X服从正态分布,考生共有1000人,估计数学成绩在75分到86分之间的人数约为人.
参考数据,
A.
261
B.
341
C.
477
D.
683
(6)近几个月来,继“共享单车”后,“共享汽车”也在我国几座大城市中悄然兴起,关系非常要好的三个家庭(每个家庭个大人,个小孩,且大人都有驾照)共人决定周末乘甲、乙两辆共享汽车出去旅游,已知每车限坐人(乘同一辆车的人不考虑位置),其中户家庭的人需乘同一辆,则户家庭恰好乘坐甲车且甲车至少有名小孩的概率为(
)
A.
B.
C.
D.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)口袋中有n个白球,3个红球,依次从口袋中任取一球,若取到红球,则继续取球,且取出的红球不放回;若取到白球,则停止取球.记取球的次数为X,若,则下列结论正确的是
A.
B.
C.
D.
(8)下列说法中错误的是???
A.
对于独立性检验,的值越大,说明两事件相关程度越大
B.
以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则c,k的值分别是和
C.
根据具有线性相关关系的两个变量的统计数据所得的回归直线方程中,
,
则
D.
通过回归直线及回归系数b,可以精确反映变量的取值和变化趋势
三、填空题:本大题共4小题,每小题5分.
(9)甲射击命中目标的概率是,乙命中目标的概率是,丙命中目标的概率是,现在三人同时射击目标,则目标被击中的概率为
.
(10)有10道数学单项选择题,每题选对得4分,不选或选错得0分.已知某考生能正确答对其中的7道题,余下的3道题每题能正确答对的概率为假设每题答对与否相互独立,记为该考生答对的题数,为该考生的得分,则________,________用数字作答.
(11)如图所示,A,B两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2,现记从中任取三条线且在单位时间内都通过的最大信息总量为X,
则P(X≥8)=
.
(12)已知随机变量的分布列如下表所示,当取最小值时,??????????,??????????.
1
2
3
P
x
y
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
2018年6月14日,第二十一届世界杯足球赛在俄罗斯拉开帷幕.赛前球迷协会组织球迷对德国、西班牙、阿根廷、巴西四支热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜.
(1)若三人中每个人可以选择任何一支球队,且选择每个球队都是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择德国队的概率为,男球迷选择德国队的概率为,记为三人中选择德国队的人数,求的分布列和数学期望.
(14)(本小题满分15分)
轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内含4小时每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内含24小时收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间假设每辆车一天内在该停车场仅停车一次,得到下面的频数分布表:
小时
频数车次
100
100
200
200
350
50
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的列联表:
男
女
合计
不超过6小时
30
6小时以上
20
合计
100
完成上述列联表,并判断能否有的把握认为“停车是否超过6小时”与性别有关?
表示某辆车一天之内含一天在该停车场停车一次所交费用,求X的概率分布列及期望;
现随机抽取该停车场内停放的3辆车,表示3辆车中停车费用大于的车辆数,求的概率.
参考公式:,其中
(15)(本小题满分15分)
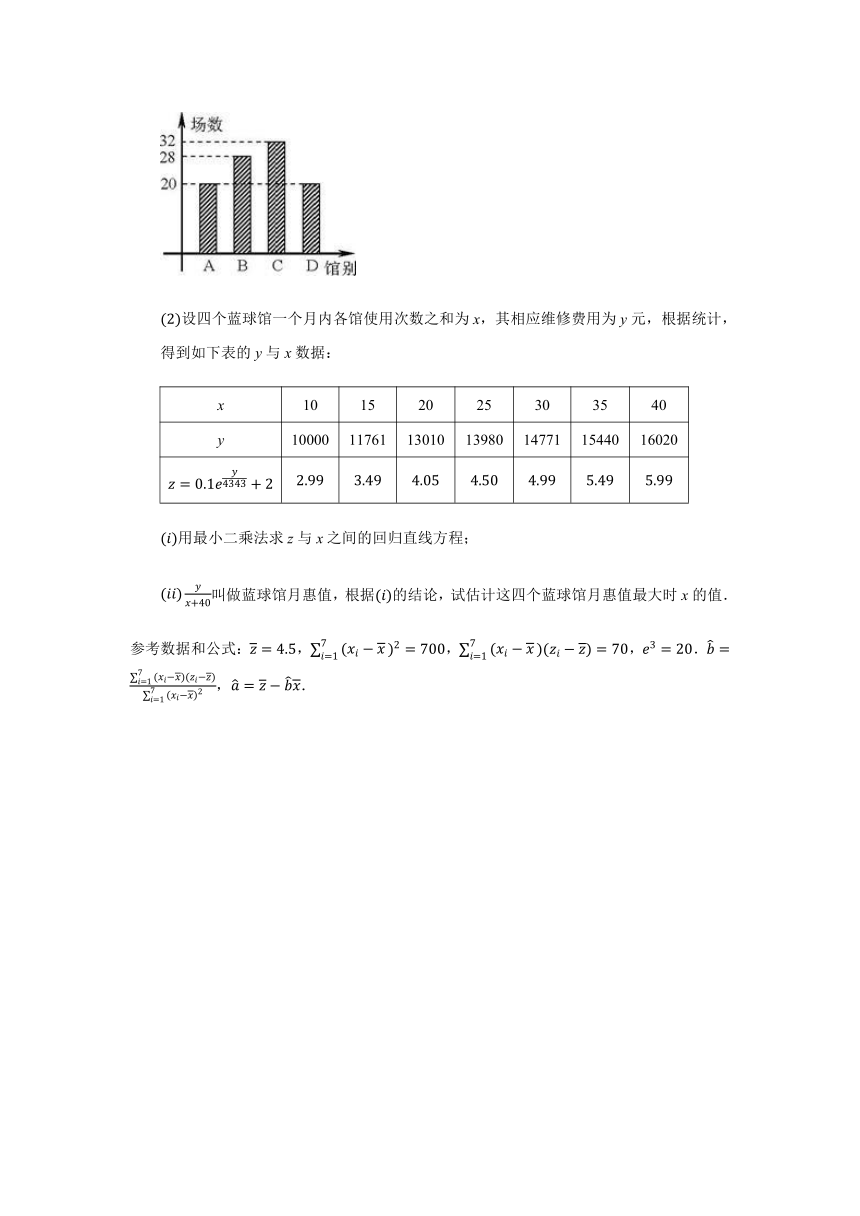
为了提高市民身体素质,某市把A,B,C,D四个蓝球馆全部转为免费民用.
在一次全民健身活动中,四个蓝球馆的使用场数如图.用分层抽样的方法从A,B,C,D四场馆的使用场数中依次抽取,,,共25场,在,,,中随机取两数,求这两数和的分布列和数学期望;
设四个蓝球馆一个月内各馆使用次数之和为x,其相应维修费用为y元,根据统计,得到如下表的y与x数据:
x
10
15
20
25
30
35
40
y
10000
11761
13010
13980
14771
15440
16020
用最小二乘法求z与x之间的回归直线方程;
叫做蓝球馆月惠值,根据的结论,试估计这四个蓝球馆月惠值最大时x的值.
参考数据和公式:,,,.,.
高中数学选修2-3《统计与概率》单元过关
形成性测试卷参考答案
一、选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)从某选手的9个得分中去掉1个最高分和1个最低分,7个剩余分数的平均分为91,由于现场做的9个分数的茎叶图有一个数据模糊无法辨认,在右图中以表示,则7个剩余分数的方差为(
)
A.
B.
C.36
D.
【解析】B
【解析】由图可知去掉的两个数是87,99,∵,∴.
∴,故选B.
(2)A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为(
)
A.
B.
C.
D.
【答案】D
【解析】由题意知模拟这三天中至少有两天有强浓雾的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三天中恰有两天有强浓雾的有:978,479、588、779,共4组随机数,
所求概率为,故选D.
(3)欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为的圆面,中间有边长为
的正方形孔,现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为(
)
A.
B.
C.
D.
【答案】A
【解析】由题意可得直径为d的圆的面积为π×=
π,而边长为的正方形面积为,
故所求概率P=,故选A.
(4)某研究机构对儿童记忆能力和识图能力进行统计分析,得到如下数据:
记忆能力
识图能力
由表中数据,求得线性回归方程为,由此估计某儿童的记忆能力为时,则他的识图能力为(
)
A.9.2
B.9.5
C.9.8
D.10
【答案】B
【解析】由表中数据得,,由点在上得,即线性回归方程为,∴当时,,即识图能力为9.5,故选B.
(5)
某中学组织了“自主招生数学选拔赛”,已知此次选拔赛的数学成绩X服从正态分布,考生共有1000人,估计数学成绩在75分到86分之间的人数约为人.
参考数据,
A.
261
B.
341
C.
477
D.
683
【答案】B
【解析】由此次选拔赛的数学成绩X服从正态分布,得正态曲线的对称轴为,,
所以数学成绩在75分到86分之间的概率,
所以数学成绩在75分到86分之间的人数约为.
故选B.
(6)近几个月来,继“共享单车”后,“共享汽车”也在我国几座大城市中悄然兴起,关系非常要好的三个家庭(每个家庭个大人,个小孩,且大人都有驾照)共人决定周末乘甲、乙两辆共享汽车出去旅游,已知每车限坐人(乘同一辆车的人不考虑位置),其中户家庭的人需乘同一辆,则户家庭恰好乘坐甲车且甲车至少有名小孩的概率为(
)
A.
B.
C.
D.
【答案】C
【解析】总的基本事件数:,
要求至少两名小孩:,
则户家庭恰好乘坐甲车且甲车至少有名小孩的概率,故选.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)口袋中有n个白球,3个红球,依次从口袋中任取一球,若取到红球,则继续取球,且取出的红球不放回;若取到白球,则停止取球.记取球的次数为X,若,则下列结论正确的是
A.
B.
C.
D.
【答案】ABC
【解析】由,得,
整理得,即,
解得舍去.共有10个球,其中3个红球,
取球次数X的所有可能取值为1,2,3,4,
,
,
,
,
所以,
.
故选ABC.
(8)下列说法中正确的是???
A.
对于独立性检验,的值越大,说明两事件相关程度越大
B.
以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则c,k的值分别是和
C.
根据具有线性相关关系的两个变量的统计数据所得的回归直线方程中,,则
D.
通过回归直线及回归系数b,可以精确反映变量的取值和变化趋势
【答案】AB
【解析】对于选项A,根据独立性检验的性质知,两个分类变量越大,说明两个分类变量相关程度越大,命题A正确;
对于选项B,由,两边取自然对数,可得,
令,得,,,则,选项B正确;
对于选项C,回归直线方程中,,选项C错误;
对于选项D,通过回归直线及回归系数b,可估计和预测变量的取值和变化趋势,选项D错误.故选A,B.
二、填空题:本大题共4小题,每小题5分。
(9)甲射击命中目标的概率是,乙命中目标的概率是,丙命中目标的概率是,现在三人同时射击目标,则目标被击中的概率为
.
【答案】
【解析】设甲命中目标为事件A,乙命中目标为事件B,丙命中目标为事件C,则击中目标表示事件A,B,C中至少有一个发生,其对立事件是A,B,C都不发生,
目标被击中的概率为.
(10)有10道数学单项选择题,每题选对得4分,不选或选错得0分.已知某考生能正确答对其中的7道题,余下的3道题每题能正确答对的概率为假设每题答对与否相互独立,记为该考生答对的题数,为该考生的得分,则________,________用数字作答.
【答案】?
?
32
【解析】由题意可知:?
,8,9,10,;
,32,36,40,,,
,
,
所以.
(11)如图所示,A,B两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2,现记从中任取三条线且在单位时间内都通过的最大信息总量为X,
则P(X≥8)=
.
【答案】
【解析】由已知得,X的取值为7,8,9,10,P(X≥8)=1-P(X=7)=1-=.
(12)已知随机变量的分布列如下表所示,当取最小值时,??????????,??????????.
1
2
3
P
x
y
【答案】;
1
2
3
P
【解析】由题意得,,
所以,
当且仅当,即,时取等号,此时随机变量的分布列为
所以
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
2018年6月14日,第二十一届世界杯足球赛在俄罗斯拉开帷幕.赛前球迷协会组织球迷对德国、西班牙、阿根廷、巴西四支热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜.
(1)若三人中每个人可以选择任何一支球队,且选择每个球队都是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择德国队的概率为,男球迷选择德国队的概率为,记为三人中选择德国队的人数,求的分布列和数学期望.
【解析】(1)设恰好有两支球队被人选择为事件,
由于三人等可能的选择四支球队中的任意一支,有种不同选择,
每种选择可能性相等,故恰好有两支球队被人选择有种不同选择,
所以.
(2)由题知,
,
,
,
∴的分布列为
∴.
(14)(本小题满分15分)
轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内含4小时每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内含24小时收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间假设每辆车一天内在该停车场仅停车一次,得到下面的频数分布表:
小时
频数车次
100
100
200
200
350
50
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的列联表:
男
女
合计
不超过6小时
30
6小时以上
20
合计
100
完成上述列联表,并判断能否有的把握认为“停车是否超过6小时”与性别有关?
表示某辆车一天之内含一天在该停车场停车一次所交费用,求X的概率分布列及期望;
现随机抽取该停车场内停放的3辆车,表示3辆车中停车费用大于的车辆数,求的概率.
参考公式:,其中
【解析】列联表如下:
男
女
合计
不超过6小时
10
30
40
6小时以上
20
40
60
合计
30
70
100
根据上表数据代入公式可得,
所以没有超过的把握认为“停车是否超过6小时”与性别有关,
由题意知,X的可能取值为5,8,11,15,19,30,
则,
,
所以X的分布列为:
X
5
8
11
15
19
30
,
由题意得,所以,
所以
.
(15)(本小题满分15分)
为了提高市民身体素质,某市把A,B,C,D四个蓝球馆全部转为免费民用.
(1)在一次全民健身活动中,四个蓝球馆的使用场数如图.用分层抽样的方法从A,B,C,D四场馆的使用场数中依次抽取,,,共25场,在,,,中随机取两数,求这两数和的分布列和数学期望;
设四个蓝球馆一个月内各馆使用次数之和为x,其相应维修费用为y元,根据统计,得到如下表的y与x数据:
x
10
15
20
25
30
35
40
y
10000
11761
13010
13980
14771
15440
16020
用最小二乘法求z与x之间的回归直线方程;
叫做蓝球馆月惠值,根据的结论,试估计这四个蓝球馆月惠值最大时x的值.
参考数据和公式:,,,.,.
10
12
13
15
P
【解析】由图可知,本次活动共100场活动,在场馆A,B,C,D使用场数分别20、28、32、20.
抽取的25场活动在场馆A,B,C,D里进行的场数,,,分别为5,7,8,5.
,12,13,15.
,
,
,
.
分布列为:
.
,,
,
由表可知,,,,
所以,z与x之间的回归直线方程为.
,
,
即.
设,
则.
,
.
令,则单调递减,
,
则在上单调递增,上单调递减,
即当时,篮球馆月惠最大.
第八单元测试卷B卷
一、选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)从某选手的9个得分中去掉1个最高分和1个最低分,7个剩余分数的平均分为91,由于现场做的9个分数的茎叶图有一个数据模糊无法辨认,在右图中以表示,则7个剩余分数的方差为(
)
A.
B.
C.36
D.
(2)A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为(
)
A.
B.
C.
D.
(3)欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为的圆面,中间有边长为
的正方形孔,现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为(
)
A.
B.
C.
D.
(4)某研究机构对儿童记忆能力和识图能力进行统计分析,得到如下数据:
记忆能力
识图能力
由表中数据,求得线性回归方程为,由此估计某儿童的记忆能力为时,则他的识图能力为(
)
A.9.2
B.9.5
C.9.8
D.10
(5)
某中学组织了“自主招生数学选拔赛”,已知此次选拔赛的数学成绩X服从正态分布,考生共有1000人,估计数学成绩在75分到86分之间的人数约为人.
参考数据,
A.
261
B.
341
C.
477
D.
683
(6)近几个月来,继“共享单车”后,“共享汽车”也在我国几座大城市中悄然兴起,关系非常要好的三个家庭(每个家庭个大人,个小孩,且大人都有驾照)共人决定周末乘甲、乙两辆共享汽车出去旅游,已知每车限坐人(乘同一辆车的人不考虑位置),其中户家庭的人需乘同一辆,则户家庭恰好乘坐甲车且甲车至少有名小孩的概率为(
)
A.
B.
C.
D.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)口袋中有n个白球,3个红球,依次从口袋中任取一球,若取到红球,则继续取球,且取出的红球不放回;若取到白球,则停止取球.记取球的次数为X,若,则下列结论正确的是
A.
B.
C.
D.
(8)下列说法中错误的是???
A.
对于独立性检验,的值越大,说明两事件相关程度越大
B.
以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则c,k的值分别是和
C.
根据具有线性相关关系的两个变量的统计数据所得的回归直线方程中,
,
则
D.
通过回归直线及回归系数b,可以精确反映变量的取值和变化趋势
三、填空题:本大题共4小题,每小题5分.
(9)甲射击命中目标的概率是,乙命中目标的概率是,丙命中目标的概率是,现在三人同时射击目标,则目标被击中的概率为
.
(10)有10道数学单项选择题,每题选对得4分,不选或选错得0分.已知某考生能正确答对其中的7道题,余下的3道题每题能正确答对的概率为假设每题答对与否相互独立,记为该考生答对的题数,为该考生的得分,则________,________用数字作答.
(11)如图所示,A,B两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2,现记从中任取三条线且在单位时间内都通过的最大信息总量为X,
则P(X≥8)=
.
(12)已知随机变量的分布列如下表所示,当取最小值时,??????????,??????????.
1
2
3
P
x
y
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
2018年6月14日,第二十一届世界杯足球赛在俄罗斯拉开帷幕.赛前球迷协会组织球迷对德国、西班牙、阿根廷、巴西四支热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜.
(1)若三人中每个人可以选择任何一支球队,且选择每个球队都是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择德国队的概率为,男球迷选择德国队的概率为,记为三人中选择德国队的人数,求的分布列和数学期望.
(14)(本小题满分15分)
轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内含4小时每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内含24小时收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间假设每辆车一天内在该停车场仅停车一次,得到下面的频数分布表:
小时
频数车次
100
100
200
200
350
50
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的列联表:
男
女
合计
不超过6小时
30
6小时以上
20
合计
100
完成上述列联表,并判断能否有的把握认为“停车是否超过6小时”与性别有关?
表示某辆车一天之内含一天在该停车场停车一次所交费用,求X的概率分布列及期望;
现随机抽取该停车场内停放的3辆车,表示3辆车中停车费用大于的车辆数,求的概率.
参考公式:,其中
(15)(本小题满分15分)
为了提高市民身体素质,某市把A,B,C,D四个蓝球馆全部转为免费民用.
在一次全民健身活动中,四个蓝球馆的使用场数如图.用分层抽样的方法从A,B,C,D四场馆的使用场数中依次抽取,,,共25场,在,,,中随机取两数,求这两数和的分布列和数学期望;
设四个蓝球馆一个月内各馆使用次数之和为x,其相应维修费用为y元,根据统计,得到如下表的y与x数据:
x
10
15
20
25
30
35
40
y
10000
11761
13010
13980
14771
15440
16020
用最小二乘法求z与x之间的回归直线方程;
叫做蓝球馆月惠值,根据的结论,试估计这四个蓝球馆月惠值最大时x的值.
参考数据和公式:,,,.,.
高中数学选修2-3《统计与概率》单元过关
形成性测试卷参考答案
一、选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)从某选手的9个得分中去掉1个最高分和1个最低分,7个剩余分数的平均分为91,由于现场做的9个分数的茎叶图有一个数据模糊无法辨认,在右图中以表示,则7个剩余分数的方差为(
)
A.
B.
C.36
D.
【解析】B
【解析】由图可知去掉的两个数是87,99,∵,∴.
∴,故选B.
(2)A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为(
)
A.
B.
C.
D.
【答案】D
【解析】由题意知模拟这三天中至少有两天有强浓雾的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三天中恰有两天有强浓雾的有:978,479、588、779,共4组随机数,
所求概率为,故选D.
(3)欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为的圆面,中间有边长为
的正方形孔,现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为(
)
A.
B.
C.
D.
【答案】A
【解析】由题意可得直径为d的圆的面积为π×=
π,而边长为的正方形面积为,
故所求概率P=,故选A.
(4)某研究机构对儿童记忆能力和识图能力进行统计分析,得到如下数据:
记忆能力
识图能力
由表中数据,求得线性回归方程为,由此估计某儿童的记忆能力为时,则他的识图能力为(
)
A.9.2
B.9.5
C.9.8
D.10
【答案】B
【解析】由表中数据得,,由点在上得,即线性回归方程为,∴当时,,即识图能力为9.5,故选B.
(5)
某中学组织了“自主招生数学选拔赛”,已知此次选拔赛的数学成绩X服从正态分布,考生共有1000人,估计数学成绩在75分到86分之间的人数约为人.
参考数据,
A.
261
B.
341
C.
477
D.
683
【答案】B
【解析】由此次选拔赛的数学成绩X服从正态分布,得正态曲线的对称轴为,,
所以数学成绩在75分到86分之间的概率,
所以数学成绩在75分到86分之间的人数约为.
故选B.
(6)近几个月来,继“共享单车”后,“共享汽车”也在我国几座大城市中悄然兴起,关系非常要好的三个家庭(每个家庭个大人,个小孩,且大人都有驾照)共人决定周末乘甲、乙两辆共享汽车出去旅游,已知每车限坐人(乘同一辆车的人不考虑位置),其中户家庭的人需乘同一辆,则户家庭恰好乘坐甲车且甲车至少有名小孩的概率为(
)
A.
B.
C.
D.
【答案】C
【解析】总的基本事件数:,
要求至少两名小孩:,
则户家庭恰好乘坐甲车且甲车至少有名小孩的概率,故选.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)口袋中有n个白球,3个红球,依次从口袋中任取一球,若取到红球,则继续取球,且取出的红球不放回;若取到白球,则停止取球.记取球的次数为X,若,则下列结论正确的是
A.
B.
C.
D.
【答案】ABC
【解析】由,得,
整理得,即,
解得舍去.共有10个球,其中3个红球,
取球次数X的所有可能取值为1,2,3,4,
,
,
,
,
所以,
.
故选ABC.
(8)下列说法中正确的是???
A.
对于独立性检验,的值越大,说明两事件相关程度越大
B.
以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则c,k的值分别是和
C.
根据具有线性相关关系的两个变量的统计数据所得的回归直线方程中,,则
D.
通过回归直线及回归系数b,可以精确反映变量的取值和变化趋势
【答案】AB
【解析】对于选项A,根据独立性检验的性质知,两个分类变量越大,说明两个分类变量相关程度越大,命题A正确;
对于选项B,由,两边取自然对数,可得,
令,得,,,则,选项B正确;
对于选项C,回归直线方程中,,选项C错误;
对于选项D,通过回归直线及回归系数b,可估计和预测变量的取值和变化趋势,选项D错误.故选A,B.
二、填空题:本大题共4小题,每小题5分。
(9)甲射击命中目标的概率是,乙命中目标的概率是,丙命中目标的概率是,现在三人同时射击目标,则目标被击中的概率为
.
【答案】
【解析】设甲命中目标为事件A,乙命中目标为事件B,丙命中目标为事件C,则击中目标表示事件A,B,C中至少有一个发生,其对立事件是A,B,C都不发生,
目标被击中的概率为.
(10)有10道数学单项选择题,每题选对得4分,不选或选错得0分.已知某考生能正确答对其中的7道题,余下的3道题每题能正确答对的概率为假设每题答对与否相互独立,记为该考生答对的题数,为该考生的得分,则________,________用数字作答.
【答案】?
?
32
【解析】由题意可知:?
,8,9,10,;
,32,36,40,,,
,
,
所以.
(11)如图所示,A,B两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2,现记从中任取三条线且在单位时间内都通过的最大信息总量为X,
则P(X≥8)=
.
【答案】
【解析】由已知得,X的取值为7,8,9,10,P(X≥8)=1-P(X=7)=1-=.
(12)已知随机变量的分布列如下表所示,当取最小值时,??????????,??????????.
1
2
3
P
x
y
【答案】;
1
2
3
P
【解析】由题意得,,
所以,
当且仅当,即,时取等号,此时随机变量的分布列为
所以
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
2018年6月14日,第二十一届世界杯足球赛在俄罗斯拉开帷幕.赛前球迷协会组织球迷对德国、西班牙、阿根廷、巴西四支热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜.
(1)若三人中每个人可以选择任何一支球队,且选择每个球队都是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择德国队的概率为,男球迷选择德国队的概率为,记为三人中选择德国队的人数,求的分布列和数学期望.
【解析】(1)设恰好有两支球队被人选择为事件,
由于三人等可能的选择四支球队中的任意一支,有种不同选择,
每种选择可能性相等,故恰好有两支球队被人选择有种不同选择,
所以.
(2)由题知,
,
,
,
∴的分布列为
∴.
(14)(本小题满分15分)
轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内含4小时每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内含24小时收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间假设每辆车一天内在该停车场仅停车一次,得到下面的频数分布表:
小时
频数车次
100
100
200
200
350
50
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的列联表:
男
女
合计
不超过6小时
30
6小时以上
20
合计
100
完成上述列联表,并判断能否有的把握认为“停车是否超过6小时”与性别有关?
表示某辆车一天之内含一天在该停车场停车一次所交费用,求X的概率分布列及期望;
现随机抽取该停车场内停放的3辆车,表示3辆车中停车费用大于的车辆数,求的概率.
参考公式:,其中
【解析】列联表如下:
男
女
合计
不超过6小时
10
30
40
6小时以上
20
40
60
合计
30
70
100
根据上表数据代入公式可得,
所以没有超过的把握认为“停车是否超过6小时”与性别有关,
由题意知,X的可能取值为5,8,11,15,19,30,
则,
,
所以X的分布列为:
X
5
8
11
15
19
30
,
由题意得,所以,
所以
.
(15)(本小题满分15分)
为了提高市民身体素质,某市把A,B,C,D四个蓝球馆全部转为免费民用.
(1)在一次全民健身活动中,四个蓝球馆的使用场数如图.用分层抽样的方法从A,B,C,D四场馆的使用场数中依次抽取,,,共25场,在,,,中随机取两数,求这两数和的分布列和数学期望;
设四个蓝球馆一个月内各馆使用次数之和为x,其相应维修费用为y元,根据统计,得到如下表的y与x数据:
x
10
15
20
25
30
35
40
y
10000
11761
13010
13980
14771
15440
16020
用最小二乘法求z与x之间的回归直线方程;
叫做蓝球馆月惠值,根据的结论,试估计这四个蓝球馆月惠值最大时x的值.
参考数据和公式:,,,.,.
10
12
13
15
P
【解析】由图可知,本次活动共100场活动,在场馆A,B,C,D使用场数分别20、28、32、20.
抽取的25场活动在场馆A,B,C,D里进行的场数,,,分别为5,7,8,5.
,12,13,15.
,
,
,
.
分布列为:
.
,,
,
由表可知,,,,
所以,z与x之间的回归直线方程为.
,
,
即.
设,
则.
,
.
令,则单调递减,
,
则在上单调递增,上单调递减,
即当时,篮球馆月惠最大.
同课章节目录
