2020-2021学年高中数学湘教版选修2-3第八章 统计与概率单元测试A卷(Word含解析)
文档属性
| 名称 | 2020-2021学年高中数学湘教版选修2-3第八章 统计与概率单元测试A卷(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览




文档简介
高中数学选修2-3《统计与概率》
第八单元测试卷A
一、单项选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值
0~50
51~100
101~150
151~200
201~300
>300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
下图是某市10月1日—20日AQI指数变化趋势:
下列叙述错误的是(
)
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
(2)在如图所示的正方形中随机投掷个点,则落入阴影部分曲线C为正态分布的密度曲线的点的个数的估计值为?
?
?
A.
B.
C.
D.
附:若,则,.
(3)某校一个课外学习小组为研究某作物种子的发芽率y和温度单位:的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据2,,得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
A.
B.
C.
D.
(4)给出以下四个说法:
残差点分布的带状区域的宽度越窄,说明拟合效果相关指数越小
在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好;
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位;
对分类变量X与Y,若它们的随机变量的观测值k越小,则判断“X与Y有关系”的把握程度越大.
其中正确的说法是??
A.
B.
C.
D.
(5)甲、乙两人进行围棋比赛,约定先连胜2局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.记X为比赛决出胜负时的总局数,则X的数学期望是
A.
B.
C.
D.
(6)设随机变量的概率分布为:
X
0
1
2
P
则X的数学期望的最小值是(
)
A.
B.0
C.2
D.随P的变化而变化
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)袋内有大小完全相同的2个黑球和3个白球,从中不放回地每次任取1个小球,直至取到白球后停止取球,则???
A.
抽取2次后停止取球的概率为
B.
停止取球时,取出的白球个数不少于黑球的概率为
C.
取球次数的期望为2
D.
取球次数的方差为
(8)已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为,则
A.
变量x与y具有正相关关系
B.
去除后的回归方程为
C.
去除后y的估计值增加速度变快
D.
去除后相应于样本点的残差为
三、填空题:本大题共4小题,每小题5分。
(9)设随机变量~,若,则
.
(10)某数学老师身高,他爷爷、父亲和儿子的身高分别是、和因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
(11)某校早上8:00上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时间到校是等可能的,则小张比小王至少早5分钟到校的概率为
.
(12)假设每架飞机的引擎在飞机中出现故障的概率为,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,若要使4引擎飞机比2引擎飞机更安全,则的取值范围是
.
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
某芯片代工厂生产某型号芯片每盒12片,每批生产若干盒,每片成本1元,每盒芯片需检验合格后方可出厂.检验方案是从每盒芯片随机取3片检验,若发现次品,就要把全盒12片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒芯片合格,不再检验,可出厂.
(Ⅰ)若某盒芯片中有9片合格,3片不合格,求该盒芯片经一次检验即可出厂的概率?
(Ⅱ)若每片芯片售价10元,每片芯片检验费用1元,次品到达组装工厂被发现后,每片须由代工厂退赔10元,并补偿1片经检验合格的芯片给组装厂.设每片芯片不合格的概率为,且相互独立.
①若某箱12片芯片中恰有3片次品的概率为,求的最大值点;
②若以①中的作为的值,由于质检员操作疏忽,有一箱芯片未经检验就被贴上合格标签出厂到组装工厂,试确定这箱芯片最终利润(单位:元)的期望.
(本小题满分15分)
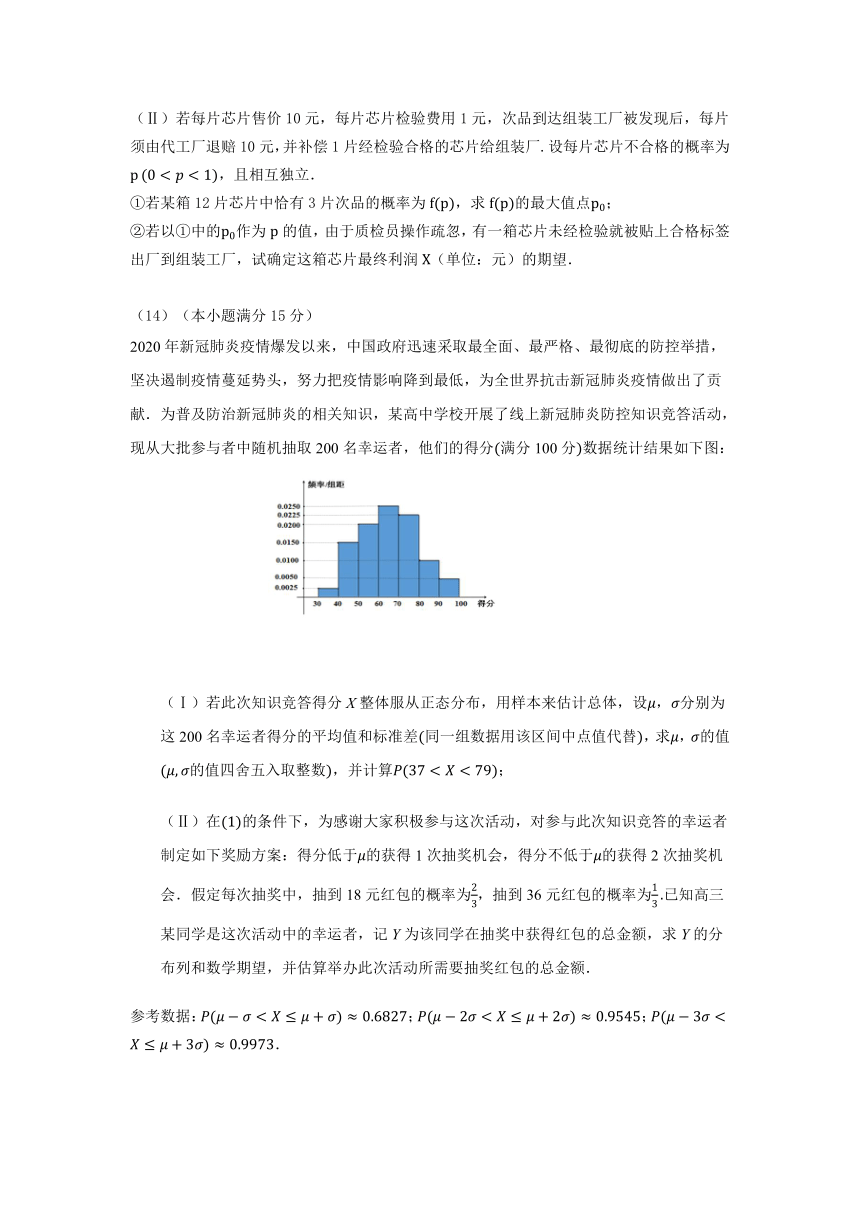
2020年新冠肺炎疫情爆发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做出了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分满分100分数据统计结果如下图:
(Ⅰ)若此次知识竞答得分X整体服从正态分布,用样本来估计总体,设,分别为这200名幸运者得分的平均值和标准差同一组数据用该区间中点值代替,求,的值的值四舍五入取整数,并计算;
(Ⅱ)在的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于的获得1次抽奖机会,得分不低于的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为,抽到36元红包的概率为已知高三某同学是这次活动中的幸运者,记Y为该同学在抽奖中获得红包的总金额,求Y的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:;;.
(15)(本小题满分15分)
为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过分时,按元/分计费;超过分时,超出部分按元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间(分)
频数
2
18
20
10
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为分.
(Ⅰ)写出王先生一次租车费用(元)与用车时间(分)的函数关系式;
(Ⅱ)若王先生一次开车时间不超过40分为“路段畅通”,设表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望;
(Ⅲ)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
高中数学选修2-3《统计与概率》单元过关
平行性测试卷A参考答案
一、单项选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值
0~50
51~100
101~150
151~200
201~300
>300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
下图是某市10月1日—20日AQI指数变化趋势:
下列叙述错误的是(
)
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
【答案】C
【解析】对,因为第10天与第11天指数值都略高100,所以中位数略高于100,正确;
对,中度污染及以上的有第11,13,14,15,17天,共5天占,正确;
对,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对,由图知,10月上旬大部分指数在100以下,10月中旬大部分指数在100以上,所以正确,故选C.
(2)在如图所示的正方形中随机投掷个点,则落入阴影部分曲线C为正态分布的密度曲线的点的个数的估计值为?
?
?
B.
C.
D.
附:若,则,
【答案】C
【解析】由,得,则阴影部分的面积为,故估计落入阴影部分的点的个数为,?
故选C.
(3)某校一个课外学习小组为研究某作物种子的发芽率y和温度单位:的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据2,,得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
A.
B.
C.
D.
【答案】D
【解析】由散点图可知,在至之间,发芽率y和温度x所对应的点在一段对数函数的曲线附近,
结合选项可知,可作为发芽率y和温度x的回归方程类型.故选:D.
(4)给出以下四个说法:
残差点分布的带状区域的宽度越窄,说明拟合效果相关指数越小
在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好;
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位;
对分类变量X与Y,若它们的随机变量的观测值k越小,则判断“X与Y有关系”的把握程度越大.
其中正确的说法是??
A.
B.
C.
D.
【答案】D
【解析】在做回归分析时,残差图中残差点分布的带状区域的宽度越窄,说明拟合精度越高,相关指数的绝对值越接近1,而不是拟合效果相关指数越小,故错误;
相关指数来刻画回归的效果,值越大,说明模型的拟合效果越好,因此正确.
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位,故正确;
对分类变量X与Y,它们的随机变量的观测值k来说,k越小,“X与Y有关系”的把握程度越小,k越大,“X与Y有关系”的把握程度越大,故错误,
故选D.
(5)甲、乙两人进行围棋比赛,约定先连胜2局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.记X为比赛决出胜负时的总局数,则X的数学期望是
A.
B.
C.
D.
【答案】C
【解析】用表示“第k局甲获胜”,表示“第k局乙获胜”,则,,,2,3,4,5,X的所有可能取值为2,3,4,5,且
,,
,.
故X的分布列为
X
2
3
4
5
P
故选C.
(6)设随机变量的概率分布为:
X
0
1
2
P
则X的数学期望的最小值是(
)
A.
B.0
C.2
D.随P的变化而变化
【答案】A
【解析】,
当时,的最小值为.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)袋内有大小完全相同的2个黑球和3个白球,从中不放回地每次任取1个小球,直至取到白球后停止取球,则???
A.
抽取2次后停止取球的概率为
B.
停止取球时,取出的白球个数不少于黑球的概率为
C.
取球次数的期望为2
D.
取球次数的方差为
【答案】BD
1
2
3
p
【解析】“抽取2次后停止取球”等价于“第1次取得黑球,第2次取得白球”,
因此抽取2次后停止取球的概率为,所以A不正确;
因为取球次数的可能取值为1,2,3,
所以,,,
因此的分布列为:
因此停止取球时,取出的白球个数不少于黑球的概率为,
即B正确;
而,因此C不正确;
,因此D正确.
故选BD.
(8)已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为,则
A.
变量x与y具有正相关关系
B.
去除后的回归方程为
C.
去除后y的估计值增加速度变快
D.
去除后相应于样本点的残差为
【答案】AB
【解析】对于A,由于去除后回归直线方程的斜率大于0,故x与y具有正相关关系,
故A正确;
对于B,除去两组数据前的回归直线方程为,且,
,故这组数据的样本中心点是,
又去除数据点和后重新求得的回归直线l的斜率为.
且去除数据点和后数据的样本中心点还是,故,
解得:,即回归直线方程为,?故B正确;
对于C,去除两个点后回归直线方程的斜率,
故去除后y的估计值增加速度变慢,故C错误;
对于D,去除两个点后回归直线方程为,
当,y估计值为,残差为,故D错误.
故选AB.
三、填空题:本大题共4小题,每小题5分。
设随机变量~,若,则
.
【答案】
【解析】,,
,.
(10)某数学老师身高,他爷爷、父亲和儿子的身高分别是、和因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
(11)某校早上8:00上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时间到校是等可能的,则小张比小王至少早5分钟到校的概率为
.
【答案】
【解析】设小张与小王的到校时间分别为7:00后第分钟,第分钟,根据题意可画出图形,如图所示,则总事件所占的面积为.小张比小王至少早5分钟到校表示的事件,如图中阴影部分所示,阴影部分所占的面积为,所以小张比小王至少早5分钟到校的概率为.
假设每架飞机的引擎在飞机中出现故障的概率为,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,若要使4引擎飞机比2引擎飞机更安全,则的取值范围是
.
【答案】
【解析】2引擎飞机安全飞行的概率是,
4引擎飞机安全飞行的概率是,
由可解得.
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
某芯片代工厂生产某型号芯片每盒12片,每批生产若干盒,每片成本1元,每盒芯片需检验合格后方可出厂.检验方案是从每盒芯片随机取3片检验,若发现次品,就要把全盒12片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒芯片合格,不再检验,可出厂.
(Ⅰ)若某盒芯片中有9片合格,3片不合格,求该盒芯片经一次检验即可出厂的概率?
(Ⅱ)若每片芯片售价10元,每片芯片检验费用1元,次品到达组装工厂被发现后,每片须由代工厂退赔10元,并补偿1片经检验合格的芯片给组装厂.设每片芯片不合格的概率为,且相互独立.
①若某箱12片芯片中恰有3片次品的概率为,求的最大值点;
②若以①中的作为的值,由于质检员操作疏忽,有一箱芯片未经检验就被贴上合格标签出厂到组装工厂,试确定这箱芯片最终利润(单位:元)的期望.
【解析】(Ⅰ)设“该盒芯片经一次检验即可出厂”的事件为A,
则
,
答:该盒芯片可出厂的概率为.
(Ⅱ)①某箱12片芯片中恰有3片次品的概率:
,
当且仅当,即时取“”号,故的最大值点.
②由题设知,,
设这箱芯片不合格品个数为,则
故,
则,
这箱芯片最终利润的期望是72元.
(14)(本小题满分15分)
2020年新冠肺炎疫情爆发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做出了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分满分100分数据统计结果如下图:
(Ⅰ)若此次知识竞答得分X整体服从正态分布,用样本来估计总体,设,分别为这200名幸运者得分的平均值和标准差同一组数据用该区间中点值代替,求,的值的值四舍五入取整数,并计算;
(Ⅱ)在的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于的获得1次抽奖机会,得分不低于的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为,抽到36元红包的概率为已知高三某同学是这次活动中的幸运者,记Y为该同学在抽奖中获得红包的总金额,求Y的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:;;.
【解析】(Ⅰ)由题意,
,
即.
.
由,则,而,故,
则X服从正态分布,
,
的取值为18,36,54,72.
由题意知,,
,
,
,,
所以Y的分布列为
Y
18
36
54
72
P
,
估算所需要抽奖红包的总金额为:元.
(15)(本小题满分15分)
为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过分时,按元/分计费;超过分时,超出部分按元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间(分)
频数
2
18
20
10
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为分.
(Ⅰ)写出王先生一次租车费用(元)与用车时间(分)的函数关系式;
(Ⅱ)若王先生一次开车时间不超过40分为“路段畅通”,设表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望;
(Ⅲ)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
【解析】(Ⅰ)当时,
当时,.
得:
(Ⅱ)王先生租用一次新能源分时租赁汽车,为“路段畅通”的概率,
可取,,,,
,,
,,
的分布列为:
.
或依题意,.
(Ⅲ)王先生租用一次新能源分时租赁汽车上下班,平均用车时间(分钟),
每次上下班租车的费用约为(元),
一个月上下班租车费用约为,
估计王先生每月的车补够上下班租用新能源分时租赁汽车用.
第八单元测试卷A
一、单项选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值
0~50
51~100
101~150
151~200
201~300
>300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
下图是某市10月1日—20日AQI指数变化趋势:
下列叙述错误的是(
)
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
(2)在如图所示的正方形中随机投掷个点,则落入阴影部分曲线C为正态分布的密度曲线的点的个数的估计值为?
?
?
A.
B.
C.
D.
附:若,则,.
(3)某校一个课外学习小组为研究某作物种子的发芽率y和温度单位:的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据2,,得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
A.
B.
C.
D.
(4)给出以下四个说法:
残差点分布的带状区域的宽度越窄,说明拟合效果相关指数越小
在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好;
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位;
对分类变量X与Y,若它们的随机变量的观测值k越小,则判断“X与Y有关系”的把握程度越大.
其中正确的说法是??
A.
B.
C.
D.
(5)甲、乙两人进行围棋比赛,约定先连胜2局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.记X为比赛决出胜负时的总局数,则X的数学期望是
A.
B.
C.
D.
(6)设随机变量的概率分布为:
X
0
1
2
P
则X的数学期望的最小值是(
)
A.
B.0
C.2
D.随P的变化而变化
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)袋内有大小完全相同的2个黑球和3个白球,从中不放回地每次任取1个小球,直至取到白球后停止取球,则???
A.
抽取2次后停止取球的概率为
B.
停止取球时,取出的白球个数不少于黑球的概率为
C.
取球次数的期望为2
D.
取球次数的方差为
(8)已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为,则
A.
变量x与y具有正相关关系
B.
去除后的回归方程为
C.
去除后y的估计值增加速度变快
D.
去除后相应于样本点的残差为
三、填空题:本大题共4小题,每小题5分。
(9)设随机变量~,若,则
.
(10)某数学老师身高,他爷爷、父亲和儿子的身高分别是、和因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
(11)某校早上8:00上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时间到校是等可能的,则小张比小王至少早5分钟到校的概率为
.
(12)假设每架飞机的引擎在飞机中出现故障的概率为,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,若要使4引擎飞机比2引擎飞机更安全,则的取值范围是
.
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
某芯片代工厂生产某型号芯片每盒12片,每批生产若干盒,每片成本1元,每盒芯片需检验合格后方可出厂.检验方案是从每盒芯片随机取3片检验,若发现次品,就要把全盒12片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒芯片合格,不再检验,可出厂.
(Ⅰ)若某盒芯片中有9片合格,3片不合格,求该盒芯片经一次检验即可出厂的概率?
(Ⅱ)若每片芯片售价10元,每片芯片检验费用1元,次品到达组装工厂被发现后,每片须由代工厂退赔10元,并补偿1片经检验合格的芯片给组装厂.设每片芯片不合格的概率为,且相互独立.
①若某箱12片芯片中恰有3片次品的概率为,求的最大值点;
②若以①中的作为的值,由于质检员操作疏忽,有一箱芯片未经检验就被贴上合格标签出厂到组装工厂,试确定这箱芯片最终利润(单位:元)的期望.
(本小题满分15分)
2020年新冠肺炎疫情爆发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做出了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分满分100分数据统计结果如下图:
(Ⅰ)若此次知识竞答得分X整体服从正态分布,用样本来估计总体,设,分别为这200名幸运者得分的平均值和标准差同一组数据用该区间中点值代替,求,的值的值四舍五入取整数,并计算;
(Ⅱ)在的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于的获得1次抽奖机会,得分不低于的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为,抽到36元红包的概率为已知高三某同学是这次活动中的幸运者,记Y为该同学在抽奖中获得红包的总金额,求Y的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:;;.
(15)(本小题满分15分)
为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过分时,按元/分计费;超过分时,超出部分按元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间(分)
频数
2
18
20
10
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为分.
(Ⅰ)写出王先生一次租车费用(元)与用车时间(分)的函数关系式;
(Ⅱ)若王先生一次开车时间不超过40分为“路段畅通”,设表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望;
(Ⅲ)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
高中数学选修2-3《统计与概率》单元过关
平行性测试卷A参考答案
一、单项选择题:本大题共6小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值
0~50
51~100
101~150
151~200
201~300
>300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
下图是某市10月1日—20日AQI指数变化趋势:
下列叙述错误的是(
)
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
【答案】C
【解析】对,因为第10天与第11天指数值都略高100,所以中位数略高于100,正确;
对,中度污染及以上的有第11,13,14,15,17天,共5天占,正确;
对,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对,由图知,10月上旬大部分指数在100以下,10月中旬大部分指数在100以上,所以正确,故选C.
(2)在如图所示的正方形中随机投掷个点,则落入阴影部分曲线C为正态分布的密度曲线的点的个数的估计值为?
?
?
B.
C.
D.
附:若,则,
【答案】C
【解析】由,得,则阴影部分的面积为,故估计落入阴影部分的点的个数为,?
故选C.
(3)某校一个课外学习小组为研究某作物种子的发芽率y和温度单位:的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据2,,得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
A.
B.
C.
D.
【答案】D
【解析】由散点图可知,在至之间,发芽率y和温度x所对应的点在一段对数函数的曲线附近,
结合选项可知,可作为发芽率y和温度x的回归方程类型.故选:D.
(4)给出以下四个说法:
残差点分布的带状区域的宽度越窄,说明拟合效果相关指数越小
在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好;
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位;
对分类变量X与Y,若它们的随机变量的观测值k越小,则判断“X与Y有关系”的把握程度越大.
其中正确的说法是??
A.
B.
C.
D.
【答案】D
【解析】在做回归分析时,残差图中残差点分布的带状区域的宽度越窄,说明拟合精度越高,相关指数的绝对值越接近1,而不是拟合效果相关指数越小,故错误;
相关指数来刻画回归的效果,值越大,说明模型的拟合效果越好,因此正确.
在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位,故正确;
对分类变量X与Y,它们的随机变量的观测值k来说,k越小,“X与Y有关系”的把握程度越小,k越大,“X与Y有关系”的把握程度越大,故错误,
故选D.
(5)甲、乙两人进行围棋比赛,约定先连胜2局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.记X为比赛决出胜负时的总局数,则X的数学期望是
A.
B.
C.
D.
【答案】C
【解析】用表示“第k局甲获胜”,表示“第k局乙获胜”,则,,,2,3,4,5,X的所有可能取值为2,3,4,5,且
,,
,.
故X的分布列为
X
2
3
4
5
P
故选C.
(6)设随机变量的概率分布为:
X
0
1
2
P
则X的数学期望的最小值是(
)
A.
B.0
C.2
D.随P的变化而变化
【答案】A
【解析】,
当时,的最小值为.
二、多项选择题:本大题共2小题,每小题5分,在每小题给出的四个选项中,至少两项是符合题目要求的.
(7)袋内有大小完全相同的2个黑球和3个白球,从中不放回地每次任取1个小球,直至取到白球后停止取球,则???
A.
抽取2次后停止取球的概率为
B.
停止取球时,取出的白球个数不少于黑球的概率为
C.
取球次数的期望为2
D.
取球次数的方差为
【答案】BD
1
2
3
p
【解析】“抽取2次后停止取球”等价于“第1次取得黑球,第2次取得白球”,
因此抽取2次后停止取球的概率为,所以A不正确;
因为取球次数的可能取值为1,2,3,
所以,,,
因此的分布列为:
因此停止取球时,取出的白球个数不少于黑球的概率为,
即B正确;
而,因此C不正确;
,因此D正确.
故选BD.
(8)已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为,则
A.
变量x与y具有正相关关系
B.
去除后的回归方程为
C.
去除后y的估计值增加速度变快
D.
去除后相应于样本点的残差为
【答案】AB
【解析】对于A,由于去除后回归直线方程的斜率大于0,故x与y具有正相关关系,
故A正确;
对于B,除去两组数据前的回归直线方程为,且,
,故这组数据的样本中心点是,
又去除数据点和后重新求得的回归直线l的斜率为.
且去除数据点和后数据的样本中心点还是,故,
解得:,即回归直线方程为,?故B正确;
对于C,去除两个点后回归直线方程的斜率,
故去除后y的估计值增加速度变慢,故C错误;
对于D,去除两个点后回归直线方程为,
当,y估计值为,残差为,故D错误.
故选AB.
三、填空题:本大题共4小题,每小题5分。
设随机变量~,若,则
.
【答案】
【解析】,,
,.
(10)某数学老师身高,他爷爷、父亲和儿子的身高分别是、和因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
(11)某校早上8:00上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时间到校是等可能的,则小张比小王至少早5分钟到校的概率为
.
【答案】
【解析】设小张与小王的到校时间分别为7:00后第分钟,第分钟,根据题意可画出图形,如图所示,则总事件所占的面积为.小张比小王至少早5分钟到校表示的事件,如图中阴影部分所示,阴影部分所占的面积为,所以小张比小王至少早5分钟到校的概率为.
假设每架飞机的引擎在飞机中出现故障的概率为,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,若要使4引擎飞机比2引擎飞机更安全,则的取值范围是
.
【答案】
【解析】2引擎飞机安全飞行的概率是,
4引擎飞机安全飞行的概率是,
由可解得.
四、解答题:解答应写出文字说明,证明过程或演算步骤.
(13)(本小题满分10分)
某芯片代工厂生产某型号芯片每盒12片,每批生产若干盒,每片成本1元,每盒芯片需检验合格后方可出厂.检验方案是从每盒芯片随机取3片检验,若发现次品,就要把全盒12片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒芯片合格,不再检验,可出厂.
(Ⅰ)若某盒芯片中有9片合格,3片不合格,求该盒芯片经一次检验即可出厂的概率?
(Ⅱ)若每片芯片售价10元,每片芯片检验费用1元,次品到达组装工厂被发现后,每片须由代工厂退赔10元,并补偿1片经检验合格的芯片给组装厂.设每片芯片不合格的概率为,且相互独立.
①若某箱12片芯片中恰有3片次品的概率为,求的最大值点;
②若以①中的作为的值,由于质检员操作疏忽,有一箱芯片未经检验就被贴上合格标签出厂到组装工厂,试确定这箱芯片最终利润(单位:元)的期望.
【解析】(Ⅰ)设“该盒芯片经一次检验即可出厂”的事件为A,
则
,
答:该盒芯片可出厂的概率为.
(Ⅱ)①某箱12片芯片中恰有3片次品的概率:
,
当且仅当,即时取“”号,故的最大值点.
②由题设知,,
设这箱芯片不合格品个数为,则
故,
则,
这箱芯片最终利润的期望是72元.
(14)(本小题满分15分)
2020年新冠肺炎疫情爆发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做出了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分满分100分数据统计结果如下图:
(Ⅰ)若此次知识竞答得分X整体服从正态分布,用样本来估计总体,设,分别为这200名幸运者得分的平均值和标准差同一组数据用该区间中点值代替,求,的值的值四舍五入取整数,并计算;
(Ⅱ)在的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于的获得1次抽奖机会,得分不低于的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为,抽到36元红包的概率为已知高三某同学是这次活动中的幸运者,记Y为该同学在抽奖中获得红包的总金额,求Y的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:;;.
【解析】(Ⅰ)由题意,
,
即.
.
由,则,而,故,
则X服从正态分布,
,
的取值为18,36,54,72.
由题意知,,
,
,
,,
所以Y的分布列为
Y
18
36
54
72
P
,
估算所需要抽奖红包的总金额为:元.
(15)(本小题满分15分)
为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过分时,按元/分计费;超过分时,超出部分按元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间(分)
频数
2
18
20
10
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为分.
(Ⅰ)写出王先生一次租车费用(元)与用车时间(分)的函数关系式;
(Ⅱ)若王先生一次开车时间不超过40分为“路段畅通”,设表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望;
(Ⅲ)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
【解析】(Ⅰ)当时,
当时,.
得:
(Ⅱ)王先生租用一次新能源分时租赁汽车,为“路段畅通”的概率,
可取,,,,
,,
,,
的分布列为:
.
或依题意,.
(Ⅲ)王先生租用一次新能源分时租赁汽车上下班,平均用车时间(分钟),
每次上下班租车的费用约为(元),
一个月上下班租车费用约为,
估计王先生每月的车补够上下班租用新能源分时租赁汽车用.
同课章节目录
