2020-2021学年青岛新版九年级上册数学期中练习试卷(word解析版)
文档属性
| 名称 | 2020-2021学年青岛新版九年级上册数学期中练习试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 11:59:49 | ||
图片预览



文档简介
2020-2021学年青岛新版九年级上册数学期中练习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.tan30°的值等于( )
A.
B.
C.1
D.2
2.如图,在Rt△ABC中,∠ACB=90°,CD是高,若AD=4BD,则的值为( )
A.
B.
C.2
D.
3.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A.
B.
C.
D.
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26°
B.52°
C.64°
D.74°
5.如图,小敏在作业中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.关于x的方程(a﹣3)﹣3x﹣2=0是一元二次方程,则( )
A.a≠±3
B.a=3
C.a=﹣3
D.a=±3
7.已知过⊙O内一点M的最长弦为10厘米,最短弦长为8厘米,则OM的长为( )
A.3厘米
B.6厘米
C.9厘米
D.厘米
8.如果关于x的一元二次方程(m﹣1)x2+2x+1=0有两个不相等的实数根,那么m的取值范围是( )
A.m>2
B.m<2
C.m>2且m≠1
D.m<2且m≠1
9.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50°
B.10sin50°
C.10tan50°
D.10cot50°
10.如图,CD是⊙O的弦,点E在圆上,EM经过圆心,且EM⊥CD于点M,若⊙O的半径为5,CD=8,则EM的长为( )
A.6
B.7
C.8
D.9
11.如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A.
B.
C.
D.
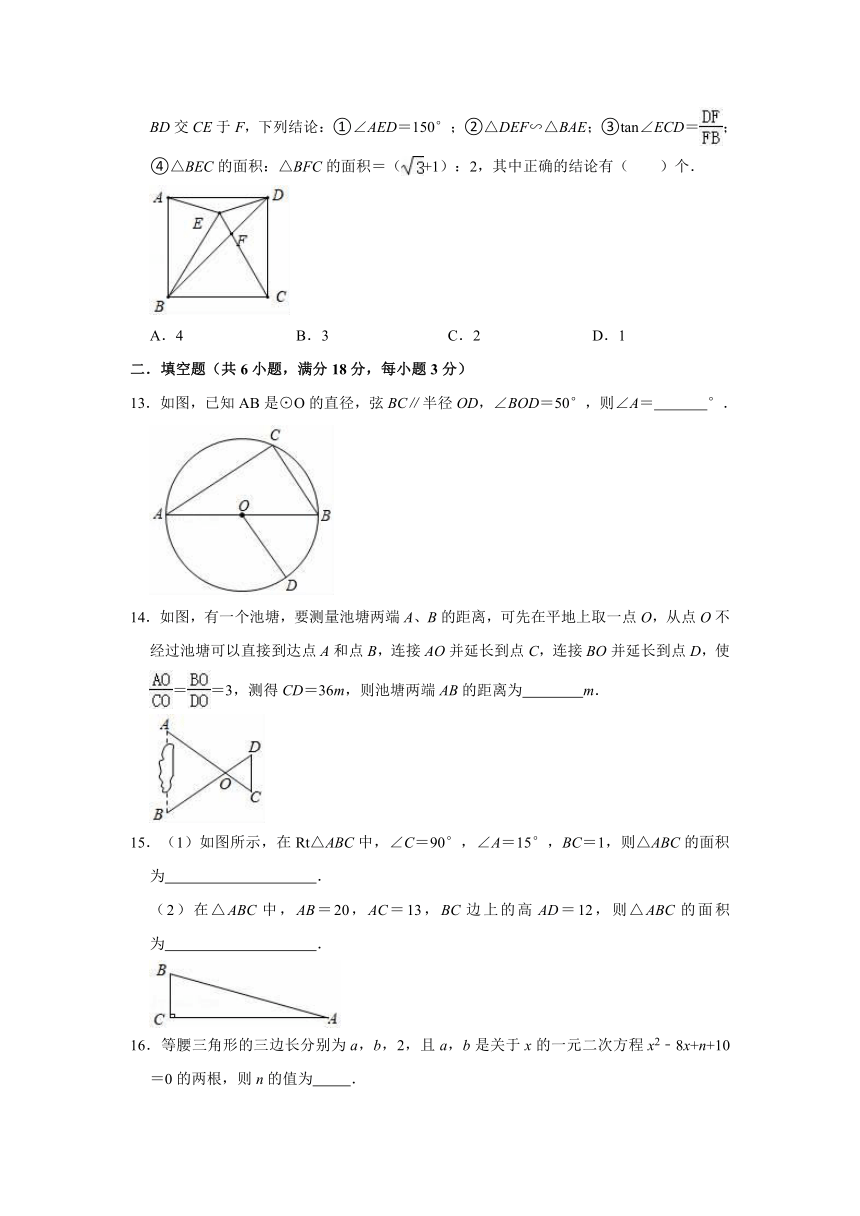
12.如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE.连接AE.DE,连接BD交CE于F,下列结论:①∠AED=150°;②△DEF∽△BAE;③tan∠ECD=;④△BEC的面积:△BFC的面积=(+1):2,其中正确的结论有( )个.
A.4
B.3
C.2
D.1
二.填空题(共6小题,满分18分,每小题3分)
13.如图,已知AB是⊙O的直径,弦BC∥半径OD,∠BOD=50°,则∠A=
°.
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为
m.
15.(1)如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,则△ABC的面积为
.
(2)在△ABC中,AB=20,AC=13,BC边上的高AD=12,则△ABC的面积为
.
16.等腰三角形的三边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣8x+n+10=0的两根,则n的值为
.
17.如图,四边形ABCD的顶点都在⊙O上,∠C=110°,则∠A=
°.
18.为解决群众看病贵的问题,我市有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元.设平均每次降价的百分率为x,则可列方程为
.
三.解答题(共7小题,满分66分)
19.(12分)解一元二次方程:
(1)2x2+5x﹣3=0;
(2)(x+2)2=3x+6.
20.(8分)如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
21.(8分)已知AD∥BC,AC、BD交于点E,AC=BC,BD=CD,BD⊥CD.
(1)求∠ACB的度数:
(2)求证:BA=BE.
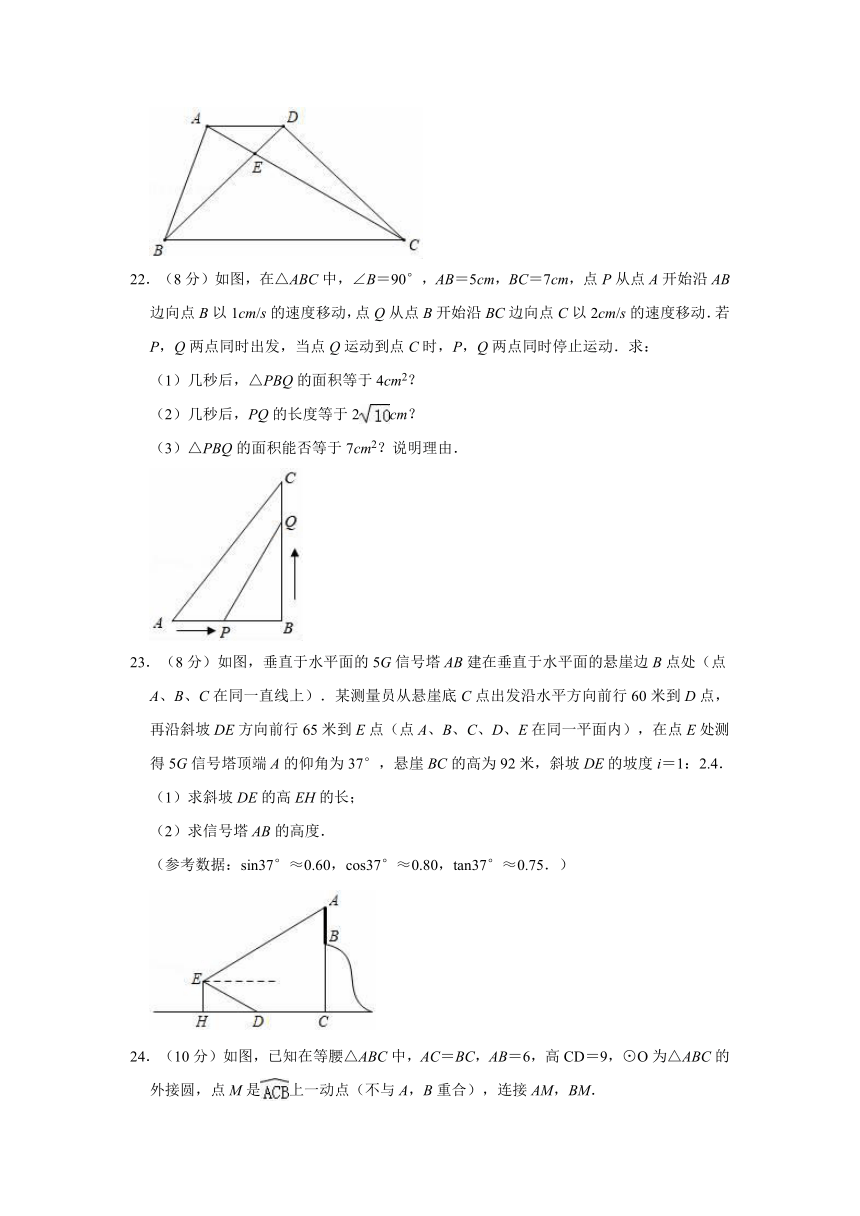
22.(8分)如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,△PBQ的面积等于4cm2?
(2)几秒后,PQ的长度等于2cm?
(3)△PBQ的面积能否等于7cm2?说明理由.
23.(8分)如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到D点,再沿斜坡DE方向前行65米到E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为37°,悬崖BC的高为92米,斜坡DE的坡度i=1:2.4.
(1)求斜坡DE的高EH的长;
(2)求信号塔AB的高度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
24.(10分)如图,已知在等腰△ABC中,AC=BC,AB=6,高CD=9,⊙O为△ABC的外接圆,点M是上一动点(不与A,B重合),连接AM,BM.
(1)如图,当射线CM与射线AB交于点E时,求证:△AMC∽△EMB;
(2)求sin∠AMB的值;
(3)当点M在上运动时,求AM?BM的最大值.
25.(12分)定义:如果一个三角形一条边上的高与这条边的比值是4:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(1)如图1,在△ABC中,AC=8,BC=5,∠ACB=30°,试判断△ABC是否是“准黄金”三角形,请说明理由.
(2)如图2,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,AD交BC的延长线于点E,若点C恰好是△ABD的重心,求的值.
(3)如图3,l1∥l2,且直线l1与l2之间的距离为4,“准黄金”△ABC的“金底”BC在直线l2上,点A在直线l1上,=,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△A′B′C,线段A′C交l1于点D.当点B′落在直线l1上时,则的值为
.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:tan30°=.
故选:A.
2.解:∵CD⊥AB,
∴∠ADC=∠CDB=90°,∠A+∠ACD=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∴∠ACD=∠B.
∴Rt△ADC∽Rt△CDB,
∴.
设BD=x,则AD=4x,
∴CD2=AD?BD=4x2,
∴CD=2x,
∴.
故选:C.
3.解:由在Rt△ABC中,∠C=90°,得
∠A+∠B=90°,
cosB=sinA=,
故选:D.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
6.解:∵关于x的方程(a﹣3)﹣3x﹣2=0是一元二次方程,
∴a2﹣7=2且a﹣3≠0,
解得:a=﹣3,
故选:C.
7.解:如图,由题意知,最长的弦为直径DE,最短的弦为垂直于直径DE的弦AB,连接OA,
则直径ED⊥AB于点M,
∵ED=10厘米,AB=8厘米,
∴OA=5厘米,AM=AB=4(厘米),
∴OM===3(厘米),
故选:A.
8.解:根据题意得m﹣1≠0且△=22﹣4(m﹣1)>0,
解得m<2且m≠1.
故选:D.
9.解:在Rt△ABC中,
∵cosB=,∠B=50°,AB=10,
∴BC=AB?cosB=10?cos50°,
故选:A.
10.解:如图,连接OC,
∵EM⊥CD,CD=8,
∴CM=MD=CD=4,
∴OM===3,
∴EM=OE+OM=5+3=8,
故选:C.
11.解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF===4,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得x=,
∴DE=EF=3﹣x=,
∴tan∠DAE===,
故选:D.
12.解:
∵△BEC为等边三角形
∴∠EBC=∠BCE=∠ECB=60°,AB=EB=EC=BC=DC
∵四边形ABCD为正方形
∴∠ABE=∠ECD=90°﹣60°=30°
∴在△ABE和△DCE中,
AB=DC
∠ABE=∠ECD
BE=EC
∴△ABE≌△DCE(SAS)
∴∠AEB=∠DEC==75°
∴∠AED=360°﹣60°﹣75°×2=150°
故①正确
由①知AE=ED
∴∠EAD=∠EDA=15°
∴∠EDF=45°﹣15°=30°
∴∠EDF=∠ABE
由①知∠AEB=∠DEC,
∴△DEF~△BAE
故②正确
过点F作FM⊥DC交于M,如图
设DM=x,则FM=x,DF=x
∵∠FCD=30°
∴MC=x
则在Rt△DBC中,BD=
∴BF=BD﹣DF=
则
∵tan∠ECD=tan30°=
∴tan∠ECD=
故③正确
如图过点E作EH⊥BC交于H,过F作FG⊥BC交于G,得
由③知MC=,MC=FG
∴FG=
∵BC=DC=x
∴BH=
∵∠EBC=60°
∴EH=x,
∴====
故④正确
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵弦BC∥半径OD,∠BOD=50°,
∴∠B=∠BOD=50°,
∵AB是⊙O的直径,
∴∠C=90°,
∴∠A=180°﹣∠C﹣∠B=40°,
故答案为:40.
14.解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
15.解:(1)以B为顶点作∠CBD=60°,交AC于D,
∵∠C=90°,∠A=15°,
∴∠ABC=75°,
∴∠ABD=15°,∠BDC=30°,
∴∠A=∠ABD,
∴AD=BD,
在Rt△BDC中,∵BC=1,
∴CD=BC?tan60°=,
∴BD=2BC=2,
∴AD=BD=2,
∴AC=2+,
∴△ABC的面积=BC?AC=×1×(2+)=.
故答案为:.
(2)△ABC中,AB=20,AC=13,BC边上高AD=12,
如图①,在Rt△ABD中AB=20,AD=12,
由勾股定理得,BD===16,
如图②,在Rt△ADC中AC=13,AD=12,
由勾股定理得,DC===5,
则BC的长为BD+DC=16+5=21或16﹣5=11,
△ABC的面积为:×21×12=126或×11×12=66.
故答案为:66或126.
16.解:当2为底边长时,则a=b,a+b=8,
∴a=b=4.
∵4,4,2能围成三角形,
∴n+10=4×4,
解得:n=6;
当2为腰长时,a、b中有一个为2,则另一个为6,
∵6,2,2不能围成三角形,
∴此种情况不存在.
故答案为:6.
17.解:∵四边形ABCD的顶点都在⊙O上,
∴∠A+∠C=180°,
∴∠A=180°﹣∠C=180°﹣110°=70°,
故答案为:70.
18.解:设平均每次降价的百分率为x,则第一降价售价为289(1﹣x),则第二次降价为289(1﹣x)2,由题意得:
289(1﹣x)2=256.
故答案为:289(1﹣x)2=256.
三.解答题(共7小题,满分66分)
19.解:(1)∵2x2+5x﹣3=0,
∴(x+3)(2x﹣1)=0,
则x+3=0或2x﹣1=0,
解得x1=﹣3,x2=0.5;
(2)∵(x+2)2=3x+6,
∴(x+2)2=3(x+2),
∴(x+2)2﹣3(x+2)=0,
则(x+2)(x﹣1)=0,
∴x+2=0或x﹣1=0,
解得x1=﹣2,x2=1.
20.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
21.解:(1)过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,
∵AD∥BC,
∴四边形AMND是矩形,
∴DN=AM,
∵BD⊥CD,BD=CD,
∴△BDC为等腰直角三角形,
∴BC=2DN=2AM,
∵AC=BC,
∴AC=2AM,
∵∠AMC为直角,
∴∠ACB=30°,
(2)证明∵∠AEB=45°+30°=75°,
∵AC=BC,
∴∠CAB=(180°﹣∠ACB)=(180﹣30)=75°,
∴∠AEB=∠EAB,
∴AB=BE.
22.解:7÷2=(s).
当运动时间为ts(0≤t≤)时,PB=(5﹣t)cm,BQ=2tcm.
(1)依题意得:×2t×(5﹣t)=4,
整理得:t2﹣5t+4=0,
解得:t1=1,t2=4(不合题意,舍去).
答:1秒后,△PBQ的面积等于4cm2.
(2)依题意得:(5﹣t)2+(2t)2=(2)2,
整理得:t2﹣2t﹣3=0,
解得:t1=3,t2=﹣1(不合题意,舍去).
答:3秒后,PQ的长度等于2cm.
(3)不能,理由如下:
依题意得:×2t×(5﹣t)=7,
整理得:t2﹣5t+7=0.
∵△=(﹣5)2﹣4×1×7=﹣3<0,
∴该方程没有实数根,
∴△PBQ的面积不能等于7cm2.
23.解:(1)过点E作EM⊥AC于点M,
∵斜坡DE的坡度(或坡比)i=1:2.4,DE=65米,CD=60米,
∴设EH=x,则DH=2.4x.
在Rt△DEH中,
∵EH2+DH2=DE2,即x2+(2.4x)2=652,
解得,x=25(米)(负值舍去),
∴EH=25米;
答:斜坡DE的高EH的长为25米;
(2)∵DH=2.4x=60(米),
∴CH=DH+DC=60+60=120(米).
∵EM⊥AC,AC⊥CD,EH⊥CD,
∴四边形EHCM是矩形,
∴EM=CH=120米,CM=EH=25米.
在Rt△AEM中,
∵∠AEM=37°,
∴AM=EM?tan37°≈120×0.75=90(米),
∴AC=AM+CM=90+25=115(米).
∴AB=AC﹣BC=115﹣92=23(米).
答:信号塔AB的高度为23米.
24.证明:(1)∵AC=BC,
∴∠CAB=∠CBA,
∵四边形ABMC是⊙O内接四边形,
∴∠ACM+∠ABM=180°,∠CAB+∠CMB=180°,
又∵∠ABM+∠MBE=180°,∠CMB+∠BME=180°,
∴∠ACM=∠MBE,∠CAB=∠BME,
∵∠AMC=∠ABC,
∴∠AMC=∠ABC=∠CAB=∠BME,
∴△AMC∽△EMB;
(2)如图1,过点A作AH⊥BC于H,
∵AC=BC,CD⊥AB,
∴AD=BD=3,
∴BC===3,
∵S△ABC=AB×CD=×BC×AH,
∴AH==,
∵∠AMB=∠ACB,
∴sin∠AMB=sin∠ACB===;
(3)如图2,过点B作BN⊥AM于N,
∵S△ABM=×AM×NB=×AM×BM×sin∠AMB,
∴S△ABM=××AM×BM,
∴AM?BM=?S△ABM,
∴当S△ABM的值最大时,AM?BM有最大值,
∴当点M与点C重合时,S△ABM的值最大,S△ABM的最大值=×6×9=27,
∴AM?BM的最大值=×27=90.
∴AM?BM的最大值为90.
25.解:(1)结论:△ABC是“准黄金”三角形,BC是“金底”.
理由:过点A作AD⊥CB交CB的延长线于D.
∵AC=8,∠C=30°,
∴AD=4,
∴=
∴△ABC是“准黄金”三角形,BC是“金底”.
(2)如图2,
∵A,D关于BC对称,
∴BE⊥AD,AE=ED,
∵△ABC是“准黄金”三角形,BC是“金底”,
∴=,
不妨设AE=4k,BC=5k,
∵C是△ABD的重心,
∴BC:CE=2:1,
∴CE=,BE=,
∴AB=,
∴.
(3).
方法一:∵△ABC是“准黄金”三角形,BC是“金底”,
∴AE:BC=4:5,
∵AE=4,
∴BC=5,
∵,
∴AB=2,
∴BE===2,
∴EC=BE+BC=7,
如图3,过点A作AE⊥BC于E,过点D作DF⊥AC于F,过点B′作B′G⊥BC于G.
在Rt△CB′G中,∵∠CGB′=90°,GB′=4,CB′=CB=5,
∴CG===3,
∵∠GCB′=∠FCD=α,∠CGB′=∠CFD=90°,
∴△CGB′∽△CFD,
∴DF:CF:CD=GB′:CG:CB′=4:3:5,
设DF=4k,CF=3k,CD=5k,
∵△AEC∽△DFA,
∴,
∴,
解得AF=7k,
∴AD===k,
∴.
方法二:如图3,同方法一求出CE=7,AE=4,
∴AC===,BC=B'C=5,
∵l1∥l2,
∴∠DAC=∠ACB,
∵∠ACB=∠A'CB',
∴∠DCB’=∠DAC,
∵∠B'DC=∠CDA,
∴△DCB’∽△DAC,
∴,
∴.
故答案为:.
一.选择题(共12小题,满分36分,每小题3分)
1.tan30°的值等于( )
A.
B.
C.1
D.2
2.如图,在Rt△ABC中,∠ACB=90°,CD是高,若AD=4BD,则的值为( )
A.
B.
C.2
D.
3.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A.
B.
C.
D.
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26°
B.52°
C.64°
D.74°
5.如图,小敏在作业中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.关于x的方程(a﹣3)﹣3x﹣2=0是一元二次方程,则( )
A.a≠±3
B.a=3
C.a=﹣3
D.a=±3
7.已知过⊙O内一点M的最长弦为10厘米,最短弦长为8厘米,则OM的长为( )
A.3厘米
B.6厘米
C.9厘米
D.厘米
8.如果关于x的一元二次方程(m﹣1)x2+2x+1=0有两个不相等的实数根,那么m的取值范围是( )
A.m>2
B.m<2
C.m>2且m≠1
D.m<2且m≠1
9.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50°
B.10sin50°
C.10tan50°
D.10cot50°
10.如图,CD是⊙O的弦,点E在圆上,EM经过圆心,且EM⊥CD于点M,若⊙O的半径为5,CD=8,则EM的长为( )
A.6
B.7
C.8
D.9
11.如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A.
B.
C.
D.
12.如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE.连接AE.DE,连接BD交CE于F,下列结论:①∠AED=150°;②△DEF∽△BAE;③tan∠ECD=;④△BEC的面积:△BFC的面积=(+1):2,其中正确的结论有( )个.
A.4
B.3
C.2
D.1
二.填空题(共6小题,满分18分,每小题3分)
13.如图,已知AB是⊙O的直径,弦BC∥半径OD,∠BOD=50°,则∠A=
°.
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为
m.
15.(1)如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,则△ABC的面积为
.
(2)在△ABC中,AB=20,AC=13,BC边上的高AD=12,则△ABC的面积为
.
16.等腰三角形的三边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣8x+n+10=0的两根,则n的值为
.
17.如图,四边形ABCD的顶点都在⊙O上,∠C=110°,则∠A=
°.
18.为解决群众看病贵的问题,我市有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元.设平均每次降价的百分率为x,则可列方程为
.
三.解答题(共7小题,满分66分)
19.(12分)解一元二次方程:
(1)2x2+5x﹣3=0;
(2)(x+2)2=3x+6.
20.(8分)如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
21.(8分)已知AD∥BC,AC、BD交于点E,AC=BC,BD=CD,BD⊥CD.
(1)求∠ACB的度数:
(2)求证:BA=BE.
22.(8分)如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)几秒后,△PBQ的面积等于4cm2?
(2)几秒后,PQ的长度等于2cm?
(3)△PBQ的面积能否等于7cm2?说明理由.
23.(8分)如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到D点,再沿斜坡DE方向前行65米到E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为37°,悬崖BC的高为92米,斜坡DE的坡度i=1:2.4.
(1)求斜坡DE的高EH的长;
(2)求信号塔AB的高度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
24.(10分)如图,已知在等腰△ABC中,AC=BC,AB=6,高CD=9,⊙O为△ABC的外接圆,点M是上一动点(不与A,B重合),连接AM,BM.
(1)如图,当射线CM与射线AB交于点E时,求证:△AMC∽△EMB;
(2)求sin∠AMB的值;
(3)当点M在上运动时,求AM?BM的最大值.
25.(12分)定义:如果一个三角形一条边上的高与这条边的比值是4:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(1)如图1,在△ABC中,AC=8,BC=5,∠ACB=30°,试判断△ABC是否是“准黄金”三角形,请说明理由.
(2)如图2,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,AD交BC的延长线于点E,若点C恰好是△ABD的重心,求的值.
(3)如图3,l1∥l2,且直线l1与l2之间的距离为4,“准黄金”△ABC的“金底”BC在直线l2上,点A在直线l1上,=,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△A′B′C,线段A′C交l1于点D.当点B′落在直线l1上时,则的值为
.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:tan30°=.
故选:A.
2.解:∵CD⊥AB,
∴∠ADC=∠CDB=90°,∠A+∠ACD=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∴∠ACD=∠B.
∴Rt△ADC∽Rt△CDB,
∴.
设BD=x,则AD=4x,
∴CD2=AD?BD=4x2,
∴CD=2x,
∴.
故选:C.
3.解:由在Rt△ABC中,∠C=90°,得
∠A+∠B=90°,
cosB=sinA=,
故选:D.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
6.解:∵关于x的方程(a﹣3)﹣3x﹣2=0是一元二次方程,
∴a2﹣7=2且a﹣3≠0,
解得:a=﹣3,
故选:C.
7.解:如图,由题意知,最长的弦为直径DE,最短的弦为垂直于直径DE的弦AB,连接OA,
则直径ED⊥AB于点M,
∵ED=10厘米,AB=8厘米,
∴OA=5厘米,AM=AB=4(厘米),
∴OM===3(厘米),
故选:A.
8.解:根据题意得m﹣1≠0且△=22﹣4(m﹣1)>0,
解得m<2且m≠1.
故选:D.
9.解:在Rt△ABC中,
∵cosB=,∠B=50°,AB=10,
∴BC=AB?cosB=10?cos50°,
故选:A.
10.解:如图,连接OC,
∵EM⊥CD,CD=8,
∴CM=MD=CD=4,
∴OM===3,
∴EM=OE+OM=5+3=8,
故选:C.
11.解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF===4,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得x=,
∴DE=EF=3﹣x=,
∴tan∠DAE===,
故选:D.
12.解:
∵△BEC为等边三角形
∴∠EBC=∠BCE=∠ECB=60°,AB=EB=EC=BC=DC
∵四边形ABCD为正方形
∴∠ABE=∠ECD=90°﹣60°=30°
∴在△ABE和△DCE中,
AB=DC
∠ABE=∠ECD
BE=EC
∴△ABE≌△DCE(SAS)
∴∠AEB=∠DEC==75°
∴∠AED=360°﹣60°﹣75°×2=150°
故①正确
由①知AE=ED
∴∠EAD=∠EDA=15°
∴∠EDF=45°﹣15°=30°
∴∠EDF=∠ABE
由①知∠AEB=∠DEC,
∴△DEF~△BAE
故②正确
过点F作FM⊥DC交于M,如图
设DM=x,则FM=x,DF=x
∵∠FCD=30°
∴MC=x
则在Rt△DBC中,BD=
∴BF=BD﹣DF=
则
∵tan∠ECD=tan30°=
∴tan∠ECD=
故③正确
如图过点E作EH⊥BC交于H,过F作FG⊥BC交于G,得
由③知MC=,MC=FG
∴FG=
∵BC=DC=x
∴BH=
∵∠EBC=60°
∴EH=x,
∴====
故④正确
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵弦BC∥半径OD,∠BOD=50°,
∴∠B=∠BOD=50°,
∵AB是⊙O的直径,
∴∠C=90°,
∴∠A=180°﹣∠C﹣∠B=40°,
故答案为:40.
14.解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
15.解:(1)以B为顶点作∠CBD=60°,交AC于D,
∵∠C=90°,∠A=15°,
∴∠ABC=75°,
∴∠ABD=15°,∠BDC=30°,
∴∠A=∠ABD,
∴AD=BD,
在Rt△BDC中,∵BC=1,
∴CD=BC?tan60°=,
∴BD=2BC=2,
∴AD=BD=2,
∴AC=2+,
∴△ABC的面积=BC?AC=×1×(2+)=.
故答案为:.
(2)△ABC中,AB=20,AC=13,BC边上高AD=12,
如图①,在Rt△ABD中AB=20,AD=12,
由勾股定理得,BD===16,
如图②,在Rt△ADC中AC=13,AD=12,
由勾股定理得,DC===5,
则BC的长为BD+DC=16+5=21或16﹣5=11,
△ABC的面积为:×21×12=126或×11×12=66.
故答案为:66或126.
16.解:当2为底边长时,则a=b,a+b=8,
∴a=b=4.
∵4,4,2能围成三角形,
∴n+10=4×4,
解得:n=6;
当2为腰长时,a、b中有一个为2,则另一个为6,
∵6,2,2不能围成三角形,
∴此种情况不存在.
故答案为:6.
17.解:∵四边形ABCD的顶点都在⊙O上,
∴∠A+∠C=180°,
∴∠A=180°﹣∠C=180°﹣110°=70°,
故答案为:70.
18.解:设平均每次降价的百分率为x,则第一降价售价为289(1﹣x),则第二次降价为289(1﹣x)2,由题意得:
289(1﹣x)2=256.
故答案为:289(1﹣x)2=256.
三.解答题(共7小题,满分66分)
19.解:(1)∵2x2+5x﹣3=0,
∴(x+3)(2x﹣1)=0,
则x+3=0或2x﹣1=0,
解得x1=﹣3,x2=0.5;
(2)∵(x+2)2=3x+6,
∴(x+2)2=3(x+2),
∴(x+2)2﹣3(x+2)=0,
则(x+2)(x﹣1)=0,
∴x+2=0或x﹣1=0,
解得x1=﹣2,x2=1.
20.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
21.解:(1)过D作BC的垂线交BC于M点,过A作BC的垂线交BC于N点,则AM∥DN,
∵AD∥BC,
∴四边形AMND是矩形,
∴DN=AM,
∵BD⊥CD,BD=CD,
∴△BDC为等腰直角三角形,
∴BC=2DN=2AM,
∵AC=BC,
∴AC=2AM,
∵∠AMC为直角,
∴∠ACB=30°,
(2)证明∵∠AEB=45°+30°=75°,
∵AC=BC,
∴∠CAB=(180°﹣∠ACB)=(180﹣30)=75°,
∴∠AEB=∠EAB,
∴AB=BE.
22.解:7÷2=(s).
当运动时间为ts(0≤t≤)时,PB=(5﹣t)cm,BQ=2tcm.
(1)依题意得:×2t×(5﹣t)=4,
整理得:t2﹣5t+4=0,
解得:t1=1,t2=4(不合题意,舍去).
答:1秒后,△PBQ的面积等于4cm2.
(2)依题意得:(5﹣t)2+(2t)2=(2)2,
整理得:t2﹣2t﹣3=0,
解得:t1=3,t2=﹣1(不合题意,舍去).
答:3秒后,PQ的长度等于2cm.
(3)不能,理由如下:
依题意得:×2t×(5﹣t)=7,
整理得:t2﹣5t+7=0.
∵△=(﹣5)2﹣4×1×7=﹣3<0,
∴该方程没有实数根,
∴△PBQ的面积不能等于7cm2.
23.解:(1)过点E作EM⊥AC于点M,
∵斜坡DE的坡度(或坡比)i=1:2.4,DE=65米,CD=60米,
∴设EH=x,则DH=2.4x.
在Rt△DEH中,
∵EH2+DH2=DE2,即x2+(2.4x)2=652,
解得,x=25(米)(负值舍去),
∴EH=25米;
答:斜坡DE的高EH的长为25米;
(2)∵DH=2.4x=60(米),
∴CH=DH+DC=60+60=120(米).
∵EM⊥AC,AC⊥CD,EH⊥CD,
∴四边形EHCM是矩形,
∴EM=CH=120米,CM=EH=25米.
在Rt△AEM中,
∵∠AEM=37°,
∴AM=EM?tan37°≈120×0.75=90(米),
∴AC=AM+CM=90+25=115(米).
∴AB=AC﹣BC=115﹣92=23(米).
答:信号塔AB的高度为23米.
24.证明:(1)∵AC=BC,
∴∠CAB=∠CBA,
∵四边形ABMC是⊙O内接四边形,
∴∠ACM+∠ABM=180°,∠CAB+∠CMB=180°,
又∵∠ABM+∠MBE=180°,∠CMB+∠BME=180°,
∴∠ACM=∠MBE,∠CAB=∠BME,
∵∠AMC=∠ABC,
∴∠AMC=∠ABC=∠CAB=∠BME,
∴△AMC∽△EMB;
(2)如图1,过点A作AH⊥BC于H,
∵AC=BC,CD⊥AB,
∴AD=BD=3,
∴BC===3,
∵S△ABC=AB×CD=×BC×AH,
∴AH==,
∵∠AMB=∠ACB,
∴sin∠AMB=sin∠ACB===;
(3)如图2,过点B作BN⊥AM于N,
∵S△ABM=×AM×NB=×AM×BM×sin∠AMB,
∴S△ABM=××AM×BM,
∴AM?BM=?S△ABM,
∴当S△ABM的值最大时,AM?BM有最大值,
∴当点M与点C重合时,S△ABM的值最大,S△ABM的最大值=×6×9=27,
∴AM?BM的最大值=×27=90.
∴AM?BM的最大值为90.
25.解:(1)结论:△ABC是“准黄金”三角形,BC是“金底”.
理由:过点A作AD⊥CB交CB的延长线于D.
∵AC=8,∠C=30°,
∴AD=4,
∴=
∴△ABC是“准黄金”三角形,BC是“金底”.
(2)如图2,
∵A,D关于BC对称,
∴BE⊥AD,AE=ED,
∵△ABC是“准黄金”三角形,BC是“金底”,
∴=,
不妨设AE=4k,BC=5k,
∵C是△ABD的重心,
∴BC:CE=2:1,
∴CE=,BE=,
∴AB=,
∴.
(3).
方法一:∵△ABC是“准黄金”三角形,BC是“金底”,
∴AE:BC=4:5,
∵AE=4,
∴BC=5,
∵,
∴AB=2,
∴BE===2,
∴EC=BE+BC=7,
如图3,过点A作AE⊥BC于E,过点D作DF⊥AC于F,过点B′作B′G⊥BC于G.
在Rt△CB′G中,∵∠CGB′=90°,GB′=4,CB′=CB=5,
∴CG===3,
∵∠GCB′=∠FCD=α,∠CGB′=∠CFD=90°,
∴△CGB′∽△CFD,
∴DF:CF:CD=GB′:CG:CB′=4:3:5,
设DF=4k,CF=3k,CD=5k,
∵△AEC∽△DFA,
∴,
∴,
解得AF=7k,
∴AD===k,
∴.
方法二:如图3,同方法一求出CE=7,AE=4,
∴AC===,BC=B'C=5,
∵l1∥l2,
∴∠DAC=∠ACB,
∵∠ACB=∠A'CB',
∴∠DCB’=∠DAC,
∵∠B'DC=∠CDA,
∴△DCB’∽△DAC,
∴,
∴.
故答案为:.
同课章节目录
