2020-2021学年青岛新版七年级上册数学期中练习试卷(word解析版)
文档属性
| 名称 | 2020-2021学年青岛新版七年级上册数学期中练习试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览




文档简介
2020-2021学年青岛新版七年级上册数学期中练习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.郑万铁路万州往郑州方向的首座隧道“天城隧道”于2018年11月30日贯通,早上品尝重庆小面,晚上享用北京烤鸭,以后这都不是梦,建造隧道的目的用下面哪个数学知识来解释最恰当( )
A.经过两点有且只有一条直线
B.过一点可以画多条直线
C.两点之间线段最短
D.连接两点之间线段的长度是两点之间的距离
2.下列事件中,最适合采用普查的是( )
A.对我校七年级一班学生出生日期的调查
B.对全国中学生节水意识的调查
C.对山东省初中学生每天阅读时间的调查
D.对某批次灯泡使用寿命的调查
3.下列说法正确的是( )
A.0无相反数,也无倒数
B.整数的相反数是整数
C.+(﹣1)的相反数是﹣1
D.数轴上原点两侧的数互为相反数
4.计算:|﹣|=( )
A.﹣
B.﹣5
C.5
D.
5.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
6.如图,对于直线AB,线段CD,射线EF,其中能相交的图是( )
A.
B.
C.
D.
7.若a、b互为相反数,c、d互为倒数,m+1的绝对值为5,则式子|m|﹣cd+的值为( )
A.3
B.3或5
C.3或﹣5
D.4
8.为了描述某支股票的价格在一段时间内的涨跌情况,以下最合适的统计图是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
9.在数轴上表示a、b两数的点如图所示,现比较a,b,﹣a,﹣b的大小,正确的是( )
A.﹣b<﹣a<b<a
B.b<﹣a<a<﹣b
C.﹣a<b<﹣b<a
D.b<a<﹣a<﹣b
10.已知|a+2|与(b﹣4)2互为相反数,则ab的结果是( )
A.﹣8
B.8
C.﹣16
D.16
11.2020年10月16日是第40个世界粮食日,某校学生会开展了“光盘行动,从我做起”的活动,对随机抽取的100名学生的在校午餐剩余量进行调查,结果有86名学生做到“光盘”,那么下列说法不合理的是( )
A.个体是每名学生是否做到光盘
B.样本容量是100
C.全校只有14名学生没有做到“光盘”
D.全校约有86%的学生做到“光盘”
12.如图,点C把线段MN分成两部分,其比为MC:CN=5:4,点P是MN的中点,PC=2cm,则MN的长为( )
A.30cm
B.36cm
C.40cm
D.48cm
二.填空题(共5小题,满分15分,每小题3分)
13.直线的基本事实:经过两点有一条直线,并且只有一条直线;简单说成:
.
14.如图,点B是线段AC上一点,点O是线段AC的中点,且AB=20,BC=8.则线段OB的长为
.
15.现把2021个连续整数1,2,3…2021的每个数的前面任意填上“+”号或者“﹣”号,然后将它们相加,则所得的结果绝对值的最小值为
.
16.某小区一天收集各类垃圾共2.4吨,绘制成各类垃圾收集量的扇形图,其中湿垃圾在扇形图中对应的圆心角为135°,那么该小区这一天湿垃圾共收集了
吨.
17.如图,按下列方法将数轴的正半轴绕在一个圆上(该圆的周长为3个单位长度,且在圆周的三等分点处分别标上了数字0、1、2).先让原点与圆周上O所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1,2,3,4.…所对应的点分别与圆周上1,2,0,1.….所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
(1)若圆周上的数字a(a是0,1,2中的一个)与数轴上的数5对应,则a=
.
(2)若数轴绕过圆周2011圈后,数轴上的一个整数点,刚好落在圆周上数字1所对应的位置,则这个整数是
.
(3)若数轴绕过圆周n(n为正整数)圈后,数轴上的一个整数点,刚好落在圆周上数字1所对应的位置,则这个整数是
.(用含n的代数式表示)
三.解答题(共8小题,满分69分)
18.(12分)计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
19.(6分)如图,在平面内有A、B、C三点.
(1)画直线AB,射线CA,线段BC;
(2)图中共有线段
条.
20.(7分)在数轴上把下列各数表示出来,并用“<”连接各数.
﹣|﹣3.5|,1,0,﹣(﹣2),﹣(+1),4
21.(8分)如图,点C,D在线段AB上,且满足CD=AD=BC,点E、F分别为线段AC,BD的中点,如果EF=10cm,求线段AB的长度.
22.(8分)小明练习跳绳.以1分钟跳165个为目标,并把20次1分钟跳绳的数量记录如表(超过165个的部分记为“+”,少于165个的部分记为“﹣”)
与目标数量的差异(单位:个)
﹣11
﹣6
﹣2
+4
+10
次数
4
5
3
6
2
(1)小明在这20次跳绳练习中,1分钟最多跳多少个?
(2)小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?
23.(8分)定义新运算“@”与“?”:a@b=,a?b=.
(1)计算3@(﹣2)﹣(﹣2)?(﹣1)的值;
(2)若A=3b@(﹣a)+a?(2﹣3b),B=a@(﹣3b)+(﹣a)?(﹣2﹣9b),比较A和B的大小.
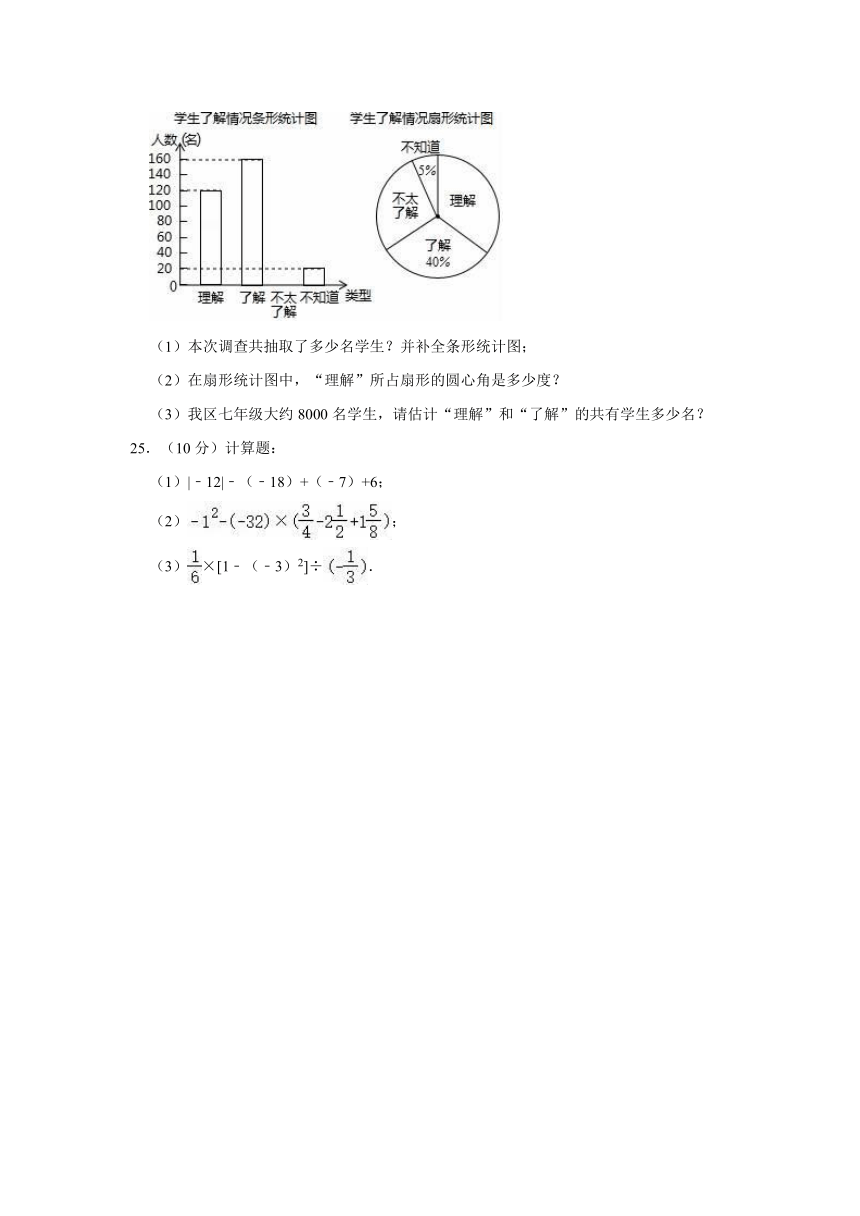
24.(10分)我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
25.(10分)计算题:
(1)|﹣12|﹣(﹣18)+(﹣7)+6;
(2);
(3)×[1﹣(﹣3)2]÷.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:用哪个数学知识来解释最恰当的是两点之间线段最短,
故选:C.
2.解:A、对我校七年级一班学生出生日期的调查适合采用普查;
B、对全国中学生节水意识的调查适合采用抽样调查;
C、对山东省初中学生每天阅读时间的调查适合采用抽样调查;
D、对某批次灯泡使用寿命的调查适合采用抽样调查;
故选:A.
3.解:A、0的相反数是0,0无倒数,故本选项错误;
B、整数的相反数是整数,正确;
C、+(﹣1)的相反数是﹣(﹣1)=1,故本选项错误;
D、数轴上原点两侧的数符号相反,但绝对值不一定相等,所以不一定互为相反数,故本选项错误.
故选:B.
4.解:,
故选:D.
5.解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选:C.
6.解:A、直线AB与线段CD不能相交,故本选项错误;
B、直线AB与射线EF能够相交,故本选项正确;
C、射线EF与线段CD不能相交,故本选项错误;
D、直线AB与射线EF不能相交,故本选项错误.
故选:B.
7.解:∵a,b互为相反数,c,d互为倒数,m+1的绝对值为5,
∴a+b=0,cd=1,|m+1|=5,
∴m=﹣6或4,
则原式=6﹣1+0=5或4﹣1+0=3.
故选:B.
8.解:根据题意,得
直观反映某种股票的涨跌情况,即变化情况.结合统计图各自的特点,应选择折线统计图.
故选:C.
9.解:由数轴可知,b<0<a,|b|>|a|,
则b<﹣a<a<﹣b,
故选:B.
10.解:∵|a+2|+(b﹣4)2=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴ab=(﹣2)4=16.
故选:D.
11.解:A、个体是每一名学生是否做到做到“光盘”情况,故A不合题意;
B、样本容量是100,故B不合题意;
C、样本中有14名学生没有做到“光盘”,故C符合题意;
D、全校约有86%的学生做到“光盘”,故D不合题意;
故选:C.
12.解:∵MC:CN=5:4,
∴设MC=5xcm,CN=4xcm,
∴MN=MC+CN=5x+4x=9x(cm),
∵点P是MN的中点,
∴PN=MN=xcm,
∴PC=PN﹣CN,
即x﹣4x=2,
解得x=4(cm),
所以,MN=9×4=36(cm),
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
13.解:直线的性质:经过两点有一条直线,并且只有一条直线.
简单地说:两点确定一条直线.
故答案为:两点确定一条直线.
14.解:如图所示:
∴AC=AB+BC,AB=20,BC=8,
∴AC=20+8=28,
又∵点O是线段AC的中点,
∴AO=CO===14,
又∵OB=OC﹣BC,
∴OB=14﹣8=6,
故答案为6.
15.解:根据绝对值的意义和题意可得,
∵2021÷4=505……1,
∴1+2﹣3﹣4+5+6﹣7﹣8+9+10﹣11﹣12+13……+2018﹣2019﹣2020+2021
=1+(2﹣3﹣4+5)+(6﹣7﹣8+9)+(10﹣11﹣12+13)+……+(2018﹣2019﹣2020+2021)
=1+0+0+……+0
=1,
故答案为:1.
16.解:2.4×=0.9(吨),
故答案为:0.9.
17.解:(1)5÷3=1…2,所以圆周上数字a与数轴上的数5对应,则a=2;
(2)数轴绕过圆周2011圈后,一个整数点落在圆周上数字1所对应的位置,这个整数是3×2011+1=6034;
(3)数轴绕过圆周n(n为正整数)圈后,一个整数点落在圆周上数字1所对应的位置,这个整数是3n+1.
故答案为:2;6034;3n+1.
三.解答题(共8小题,满分69分)
18.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
19.解:(1)如图,直线AB,射线CA,线段BC即为所求;
(2)图中共有线段3条.
故答案为:3.
20.解:在数轴上把各数表示出来为:
用“<”连接各数为:﹣|﹣3.5|<﹣(+1)<0<1<﹣(﹣2)<4.
21.解:∵CD=AD=BC,
∴AD=4CD,BC=6CD,
∵点E、F分别为线段AC,BD的中点,
∴EC=AC=(AD﹣CD)=1.5CD,DF=BD=(BC﹣CD)=2.5CD,
∵EF=10cm,
∴EF=EC+DC+DF=5CD=10cm,
∴CD=2cm,
∴AB=AD+BD=AD+BC﹣CD=9CD=18cm.
22.解:(1)跳绳最多的一次为:165+10=175(个)
答:小明在这20次跳绳练习中,1分钟最多跳175个.
(2)(+10)﹣(﹣11)=10+11=21(个)
答:小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多21个.
(3)165×20﹣11×4﹣6×5﹣2×3+4×6+10×2=3264(个)
答:小明在这20次跳绳练习中,累计跳绳3264个.
23.解:(1)3@(﹣2)﹣(﹣2)?(﹣1)
=﹣
=+
=1;
(2)A=3b@(﹣a)+a?(2﹣3b)
=+
=3b﹣1,
B=a@(﹣3b)+(﹣a)?(﹣2﹣9b)
=+
=3b+1,
则A<B.
24.解:(1)本次调查共抽取学生为:=400(名),
∴不太了解的学生为:400﹣120﹣160﹣20=100(名),
补全条形统计图如下:
(2)“理解”所占扇形的圆心角是:×360°=108°;
(3)8000×(40%+)=5600(名),
所以“理解”和“了解”的共有学生5600名.
25.解:(1)|﹣12|﹣(﹣18)+(﹣7)+6
=12+18+(﹣7)+6
=30+(﹣7)+6
=23+6
=29;
(2)
=﹣1+32×(﹣+)
=﹣1+32×﹣32×+32×
=﹣1+24﹣80+52
=﹣5;
(3)×[1﹣(﹣3)2]÷
=×(1﹣9)×(﹣3)
=×(﹣8)×(﹣3)
=4.
一.选择题(共12小题,满分36分,每小题3分)
1.郑万铁路万州往郑州方向的首座隧道“天城隧道”于2018年11月30日贯通,早上品尝重庆小面,晚上享用北京烤鸭,以后这都不是梦,建造隧道的目的用下面哪个数学知识来解释最恰当( )
A.经过两点有且只有一条直线
B.过一点可以画多条直线
C.两点之间线段最短
D.连接两点之间线段的长度是两点之间的距离
2.下列事件中,最适合采用普查的是( )
A.对我校七年级一班学生出生日期的调查
B.对全国中学生节水意识的调查
C.对山东省初中学生每天阅读时间的调查
D.对某批次灯泡使用寿命的调查
3.下列说法正确的是( )
A.0无相反数,也无倒数
B.整数的相反数是整数
C.+(﹣1)的相反数是﹣1
D.数轴上原点两侧的数互为相反数
4.计算:|﹣|=( )
A.﹣
B.﹣5
C.5
D.
5.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
6.如图,对于直线AB,线段CD,射线EF,其中能相交的图是( )
A.
B.
C.
D.
7.若a、b互为相反数,c、d互为倒数,m+1的绝对值为5,则式子|m|﹣cd+的值为( )
A.3
B.3或5
C.3或﹣5
D.4
8.为了描述某支股票的价格在一段时间内的涨跌情况,以下最合适的统计图是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
9.在数轴上表示a、b两数的点如图所示,现比较a,b,﹣a,﹣b的大小,正确的是( )
A.﹣b<﹣a<b<a
B.b<﹣a<a<﹣b
C.﹣a<b<﹣b<a
D.b<a<﹣a<﹣b
10.已知|a+2|与(b﹣4)2互为相反数,则ab的结果是( )
A.﹣8
B.8
C.﹣16
D.16
11.2020年10月16日是第40个世界粮食日,某校学生会开展了“光盘行动,从我做起”的活动,对随机抽取的100名学生的在校午餐剩余量进行调查,结果有86名学生做到“光盘”,那么下列说法不合理的是( )
A.个体是每名学生是否做到光盘
B.样本容量是100
C.全校只有14名学生没有做到“光盘”
D.全校约有86%的学生做到“光盘”
12.如图,点C把线段MN分成两部分,其比为MC:CN=5:4,点P是MN的中点,PC=2cm,则MN的长为( )
A.30cm
B.36cm
C.40cm
D.48cm
二.填空题(共5小题,满分15分,每小题3分)
13.直线的基本事实:经过两点有一条直线,并且只有一条直线;简单说成:
.
14.如图,点B是线段AC上一点,点O是线段AC的中点,且AB=20,BC=8.则线段OB的长为
.
15.现把2021个连续整数1,2,3…2021的每个数的前面任意填上“+”号或者“﹣”号,然后将它们相加,则所得的结果绝对值的最小值为
.
16.某小区一天收集各类垃圾共2.4吨,绘制成各类垃圾收集量的扇形图,其中湿垃圾在扇形图中对应的圆心角为135°,那么该小区这一天湿垃圾共收集了
吨.
17.如图,按下列方法将数轴的正半轴绕在一个圆上(该圆的周长为3个单位长度,且在圆周的三等分点处分别标上了数字0、1、2).先让原点与圆周上O所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1,2,3,4.…所对应的点分别与圆周上1,2,0,1.….所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
(1)若圆周上的数字a(a是0,1,2中的一个)与数轴上的数5对应,则a=
.
(2)若数轴绕过圆周2011圈后,数轴上的一个整数点,刚好落在圆周上数字1所对应的位置,则这个整数是
.
(3)若数轴绕过圆周n(n为正整数)圈后,数轴上的一个整数点,刚好落在圆周上数字1所对应的位置,则这个整数是
.(用含n的代数式表示)
三.解答题(共8小题,满分69分)
18.(12分)计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
19.(6分)如图,在平面内有A、B、C三点.
(1)画直线AB,射线CA,线段BC;
(2)图中共有线段
条.
20.(7分)在数轴上把下列各数表示出来,并用“<”连接各数.
﹣|﹣3.5|,1,0,﹣(﹣2),﹣(+1),4
21.(8分)如图,点C,D在线段AB上,且满足CD=AD=BC,点E、F分别为线段AC,BD的中点,如果EF=10cm,求线段AB的长度.
22.(8分)小明练习跳绳.以1分钟跳165个为目标,并把20次1分钟跳绳的数量记录如表(超过165个的部分记为“+”,少于165个的部分记为“﹣”)
与目标数量的差异(单位:个)
﹣11
﹣6
﹣2
+4
+10
次数
4
5
3
6
2
(1)小明在这20次跳绳练习中,1分钟最多跳多少个?
(2)小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?
23.(8分)定义新运算“@”与“?”:a@b=,a?b=.
(1)计算3@(﹣2)﹣(﹣2)?(﹣1)的值;
(2)若A=3b@(﹣a)+a?(2﹣3b),B=a@(﹣3b)+(﹣a)?(﹣2﹣9b),比较A和B的大小.
24.(10分)我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
25.(10分)计算题:
(1)|﹣12|﹣(﹣18)+(﹣7)+6;
(2);
(3)×[1﹣(﹣3)2]÷.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:用哪个数学知识来解释最恰当的是两点之间线段最短,
故选:C.
2.解:A、对我校七年级一班学生出生日期的调查适合采用普查;
B、对全国中学生节水意识的调查适合采用抽样调查;
C、对山东省初中学生每天阅读时间的调查适合采用抽样调查;
D、对某批次灯泡使用寿命的调查适合采用抽样调查;
故选:A.
3.解:A、0的相反数是0,0无倒数,故本选项错误;
B、整数的相反数是整数,正确;
C、+(﹣1)的相反数是﹣(﹣1)=1,故本选项错误;
D、数轴上原点两侧的数符号相反,但绝对值不一定相等,所以不一定互为相反数,故本选项错误.
故选:B.
4.解:,
故选:D.
5.解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选:C.
6.解:A、直线AB与线段CD不能相交,故本选项错误;
B、直线AB与射线EF能够相交,故本选项正确;
C、射线EF与线段CD不能相交,故本选项错误;
D、直线AB与射线EF不能相交,故本选项错误.
故选:B.
7.解:∵a,b互为相反数,c,d互为倒数,m+1的绝对值为5,
∴a+b=0,cd=1,|m+1|=5,
∴m=﹣6或4,
则原式=6﹣1+0=5或4﹣1+0=3.
故选:B.
8.解:根据题意,得
直观反映某种股票的涨跌情况,即变化情况.结合统计图各自的特点,应选择折线统计图.
故选:C.
9.解:由数轴可知,b<0<a,|b|>|a|,
则b<﹣a<a<﹣b,
故选:B.
10.解:∵|a+2|+(b﹣4)2=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴ab=(﹣2)4=16.
故选:D.
11.解:A、个体是每一名学生是否做到做到“光盘”情况,故A不合题意;
B、样本容量是100,故B不合题意;
C、样本中有14名学生没有做到“光盘”,故C符合题意;
D、全校约有86%的学生做到“光盘”,故D不合题意;
故选:C.
12.解:∵MC:CN=5:4,
∴设MC=5xcm,CN=4xcm,
∴MN=MC+CN=5x+4x=9x(cm),
∵点P是MN的中点,
∴PN=MN=xcm,
∴PC=PN﹣CN,
即x﹣4x=2,
解得x=4(cm),
所以,MN=9×4=36(cm),
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
13.解:直线的性质:经过两点有一条直线,并且只有一条直线.
简单地说:两点确定一条直线.
故答案为:两点确定一条直线.
14.解:如图所示:
∴AC=AB+BC,AB=20,BC=8,
∴AC=20+8=28,
又∵点O是线段AC的中点,
∴AO=CO===14,
又∵OB=OC﹣BC,
∴OB=14﹣8=6,
故答案为6.
15.解:根据绝对值的意义和题意可得,
∵2021÷4=505……1,
∴1+2﹣3﹣4+5+6﹣7﹣8+9+10﹣11﹣12+13……+2018﹣2019﹣2020+2021
=1+(2﹣3﹣4+5)+(6﹣7﹣8+9)+(10﹣11﹣12+13)+……+(2018﹣2019﹣2020+2021)
=1+0+0+……+0
=1,
故答案为:1.
16.解:2.4×=0.9(吨),
故答案为:0.9.
17.解:(1)5÷3=1…2,所以圆周上数字a与数轴上的数5对应,则a=2;
(2)数轴绕过圆周2011圈后,一个整数点落在圆周上数字1所对应的位置,这个整数是3×2011+1=6034;
(3)数轴绕过圆周n(n为正整数)圈后,一个整数点落在圆周上数字1所对应的位置,这个整数是3n+1.
故答案为:2;6034;3n+1.
三.解答题(共8小题,满分69分)
18.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
19.解:(1)如图,直线AB,射线CA,线段BC即为所求;
(2)图中共有线段3条.
故答案为:3.
20.解:在数轴上把各数表示出来为:
用“<”连接各数为:﹣|﹣3.5|<﹣(+1)<0<1<﹣(﹣2)<4.
21.解:∵CD=AD=BC,
∴AD=4CD,BC=6CD,
∵点E、F分别为线段AC,BD的中点,
∴EC=AC=(AD﹣CD)=1.5CD,DF=BD=(BC﹣CD)=2.5CD,
∵EF=10cm,
∴EF=EC+DC+DF=5CD=10cm,
∴CD=2cm,
∴AB=AD+BD=AD+BC﹣CD=9CD=18cm.
22.解:(1)跳绳最多的一次为:165+10=175(个)
答:小明在这20次跳绳练习中,1分钟最多跳175个.
(2)(+10)﹣(﹣11)=10+11=21(个)
答:小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多21个.
(3)165×20﹣11×4﹣6×5﹣2×3+4×6+10×2=3264(个)
答:小明在这20次跳绳练习中,累计跳绳3264个.
23.解:(1)3@(﹣2)﹣(﹣2)?(﹣1)
=﹣
=+
=1;
(2)A=3b@(﹣a)+a?(2﹣3b)
=+
=3b﹣1,
B=a@(﹣3b)+(﹣a)?(﹣2﹣9b)
=+
=3b+1,
则A<B.
24.解:(1)本次调查共抽取学生为:=400(名),
∴不太了解的学生为:400﹣120﹣160﹣20=100(名),
补全条形统计图如下:
(2)“理解”所占扇形的圆心角是:×360°=108°;
(3)8000×(40%+)=5600(名),
所以“理解”和“了解”的共有学生5600名.
25.解:(1)|﹣12|﹣(﹣18)+(﹣7)+6
=12+18+(﹣7)+6
=30+(﹣7)+6
=23+6
=29;
(2)
=﹣1+32×(﹣+)
=﹣1+32×﹣32×+32×
=﹣1+24﹣80+52
=﹣5;
(3)×[1﹣(﹣3)2]÷
=×(1﹣9)×(﹣3)
=×(﹣8)×(﹣3)
=4.
同课章节目录
