人教版必修1高一上册数学课件第二章 函数《2.4函数与方程思想》(17张PPT)
文档属性
| 名称 | 人教版必修1高一上册数学课件第二章 函数《2.4函数与方程思想》(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 441.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览





文档简介
专题一:函数与方程思想
一、知识整合
1、函数的思想:
用运动和变化的观点,分析两个变量的关系,通过构造函数
并运用函数的图像和性质解决相关问题。
2、方程的思想:
根据两个变量间的等量关系,通过建立方程(组)解决相关问题。
3、函数与方程的联系:
4、函数与方程思想的应用:
解决:不等式、导数、数列、向量、三角、解析几何、立体几何等相关问题。
二、典型例题
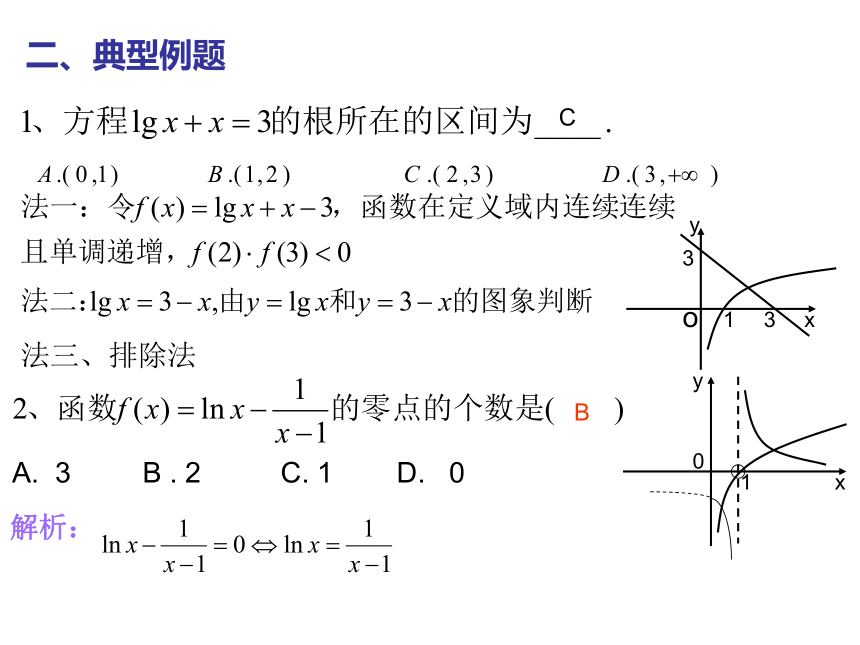
3
3
x
y
1
o
解析:
A. 3 B . 2 C. 1 D. 0
x
y
1
0
C
B
解析:
o
x
y
a>1
o
x
y
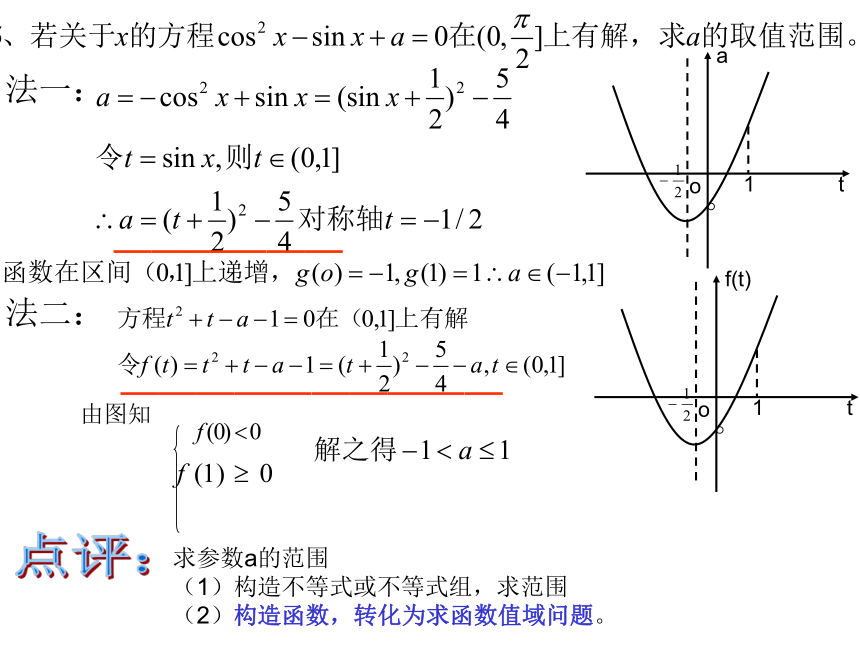
0 三个小题的共性:可以将方程问题转化为函数问题解决,体现了函数与方程思想的应用。
解析:
通过构造函数把不等式问题转化为函数问题解决。
B
法一:
法二:
t
a
o
1
t
f(t)
o
1
由图知
求参数a的范围
(1)构造不等式或不等式组,求范围
(2)构造函数,转化为求函数值域问题。
——————
——————————
解:
变式:
0
1
a
f(a)
0
1
a
f(a)
0
1
a
f(a)
则
即
在解决多个变量问题时,分清“主元”是关键
————————————————
x
o
1
-1
g(x)
则
x
h(x)
1
-1
5
0
本题涉及函数、导数、不等式、向量等多个知识点,运用了
函数与方程、数形结合、分类讨论、化归与转化的数学思想。
_________________
_________________________
8、若不等式
对一切
恒成立,试求实数
的最大整数值.
数列是特殊的函数,数列问题可以转化成函数问题。
三、课堂小结:
1、函数问题可以转化为方程问题去解决,
方程问题可以转化为函数问题去解决。
2、求参数范围问题常用两条途径:
(1)构造不等式或不等式组:
(2)建立函数关系:转化为求函数的值域
3、在多个字母变量问题中,选准主“元”是解题的关键
4、函数与方程思想广泛应用于不等式、导数、数列
向量、三角(解析几何、立体几何、实际问题)等
四、课后练习
解析:
0
1
a>o
0
1
a<0
解析:
2
4
x
y
t=-(4+a)/2
o
4、已知函数
(
),若
在区间
上是单调减函数,试求
的最小值.
y
3
x
o
-1
3
A
B
4、已知函数
(
),若
在区间
上是单调减函数,试求
的最小值.
∵
在区间
上是单调减函数,
在区间[-1,2]上恒成立.
解:
根据二次函数图象可知
且
,
O
x
y
-1
2
即:
也即
作出不等式组表示的平面区域如图:
2a+b-1=0
b
4a-b+4=0
z=a+b
a
P (- ,2)
-
1
2
,
当直线
经过交点
时,
取得最小值
∴
取得最小值为
y
3
x
o
-1
3
A
B
y
x
0
4
3
三、课堂小结:
通过本节练习可以看出,运用函数与方程思想,可以解决不等式、导数、数列、向量、三角的相关问题,除此以外,还可以解决解析几何、立体几何的问题。
一、知识整合
1、函数的思想:
用运动和变化的观点,分析两个变量的关系,通过构造函数
并运用函数的图像和性质解决相关问题。
2、方程的思想:
根据两个变量间的等量关系,通过建立方程(组)解决相关问题。
3、函数与方程的联系:
4、函数与方程思想的应用:
解决:不等式、导数、数列、向量、三角、解析几何、立体几何等相关问题。
二、典型例题
3
3
x
y
1
o
解析:
A. 3 B . 2 C. 1 D. 0
x
y
1
0
C
B
解析:
o
x
y
a>1
o
x
y
0
解析:
通过构造函数把不等式问题转化为函数问题解决。
B
法一:
法二:
t
a
o
1
t
f(t)
o
1
由图知
求参数a的范围
(1)构造不等式或不等式组,求范围
(2)构造函数,转化为求函数值域问题。
——————
——————————
解:
变式:
0
1
a
f(a)
0
1
a
f(a)
0
1
a
f(a)
则
即
在解决多个变量问题时,分清“主元”是关键
————————————————
x
o
1
-1
g(x)
则
x
h(x)
1
-1
5
0
本题涉及函数、导数、不等式、向量等多个知识点,运用了
函数与方程、数形结合、分类讨论、化归与转化的数学思想。
_________________
_________________________
8、若不等式
对一切
恒成立,试求实数
的最大整数值.
数列是特殊的函数,数列问题可以转化成函数问题。
三、课堂小结:
1、函数问题可以转化为方程问题去解决,
方程问题可以转化为函数问题去解决。
2、求参数范围问题常用两条途径:
(1)构造不等式或不等式组:
(2)建立函数关系:转化为求函数的值域
3、在多个字母变量问题中,选准主“元”是解题的关键
4、函数与方程思想广泛应用于不等式、导数、数列
向量、三角(解析几何、立体几何、实际问题)等
四、课后练习
解析:
0
1
a>o
0
1
a<0
解析:
2
4
x
y
t=-(4+a)/2
o
4、已知函数
(
),若
在区间
上是单调减函数,试求
的最小值.
y
3
x
o
-1
3
A
B
4、已知函数
(
),若
在区间
上是单调减函数,试求
的最小值.
∵
在区间
上是单调减函数,
在区间[-1,2]上恒成立.
解:
根据二次函数图象可知
且
,
O
x
y
-1
2
即:
也即
作出不等式组表示的平面区域如图:
2a+b-1=0
b
4a-b+4=0
z=a+b
a
P (- ,2)
-
1
2
,
当直线
经过交点
时,
取得最小值
∴
取得最小值为
y
3
x
o
-1
3
A
B
y
x
0
4
3
三、课堂小结:
通过本节练习可以看出,运用函数与方程思想,可以解决不等式、导数、数列、向量、三角的相关问题,除此以外,还可以解决解析几何、立体几何的问题。
