人教版高一上册数学课件《线面平行的性质》(19张PPT)
文档属性
| 名称 | 人教版高一上册数学课件《线面平行的性质》(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 528.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 16:27:17 | ||
图片预览




文档简介
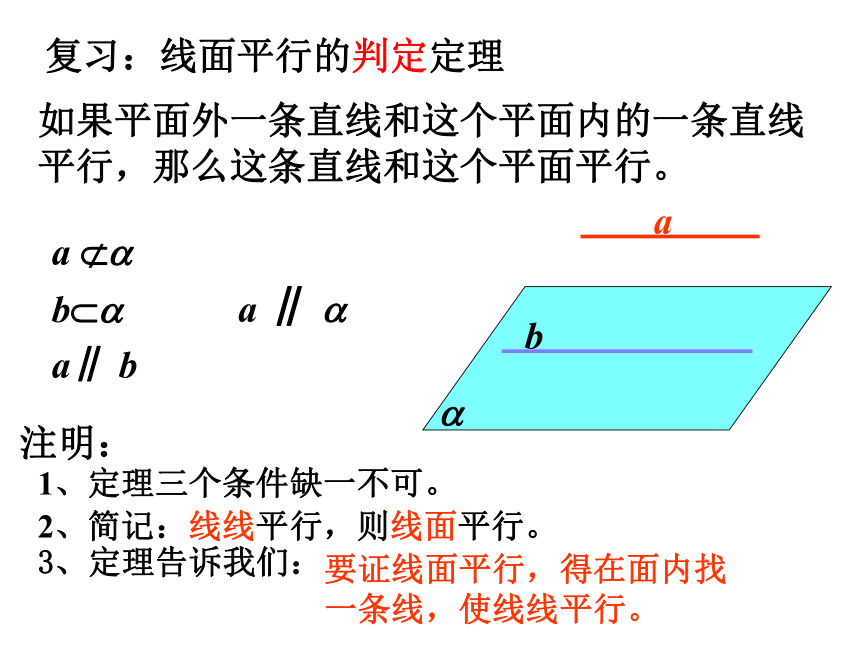
复习:线面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
b
a
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
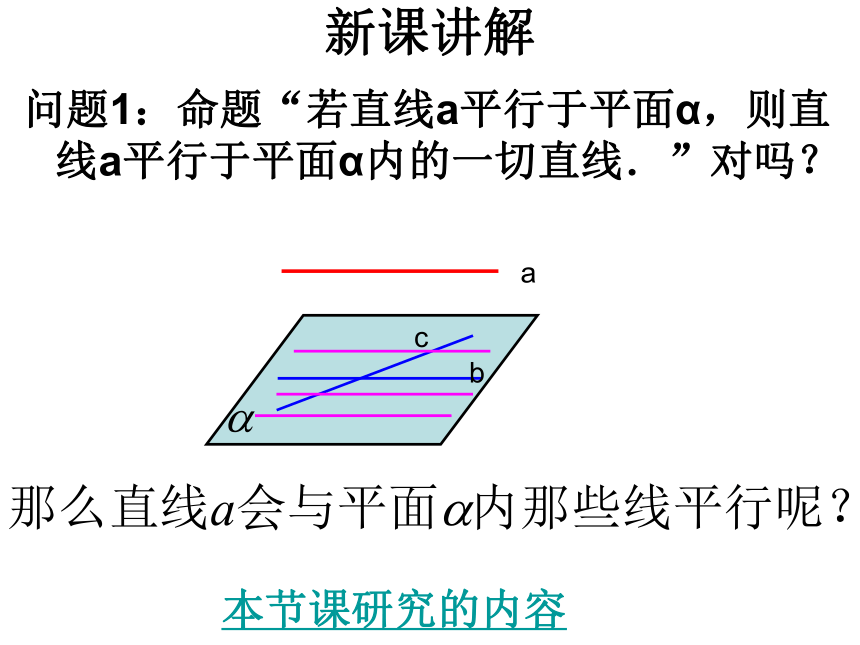
新课讲解
问题1:命题“若直线a平行于平面α,则直 线a平行于平面α内的一切直线.”对吗?
a
b
c
本节课研究的内容
?
b
a
?
证明:
新课:直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
?
b
a
?
注意:
1、定理三个条件缺一不可。
2、简记:线面平行,则线线平行。
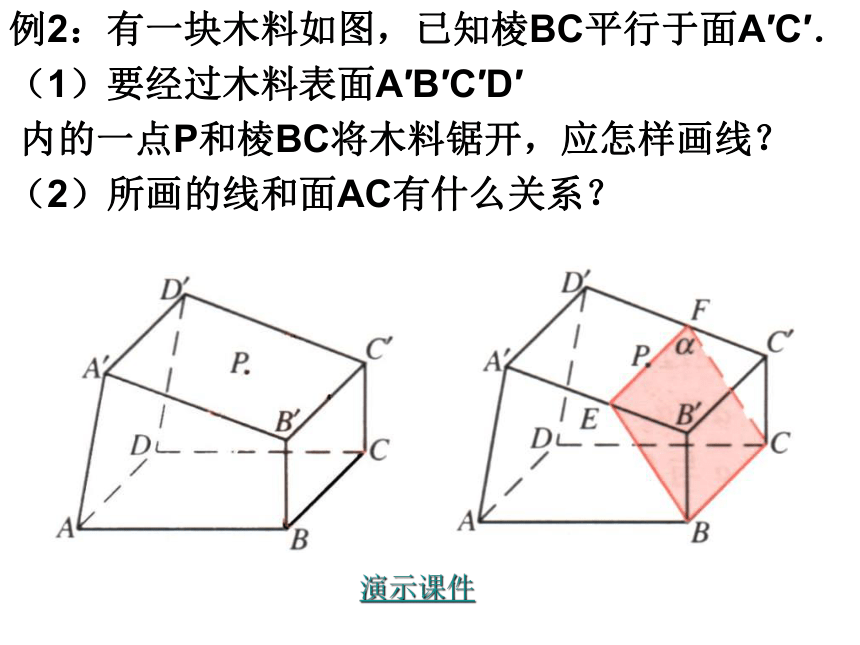
例2:有一块木料如图,已知棱BC平行于面A′C′.
(1)要经过木料表面A′B′C′D′
内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC有什么关系?
演示课件
线//线
线//面
转化是立体几何的一种重要的思想方法
说明:
证明:
P62习题5
已知:如图,AB//平面 ,AC//BD,且 AC、BD与 分别相 交于点C, D.
求证:AC=BD
练习
小结
证明线面平行的
转化思想:
线//线
线//面
面//面
(1)平行公理
(2)三角形中位线
(3)平行线分线段成比例
(4)相似三角形对应边成比例
(5)平行四边形对边平行
练习
四、课堂练习:
(1)以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )
(2)如果直线a、b和平面α 满足a ∥ α,
b ∥ α,那么a ∥ b ;( )
(3)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α, 那么 b ∥ α;( )
(4)过平面外一点和这个平面平行的直线只有一条.( )
填空:
(2)若两直线a、b相交,且a ∥ α,则b与α的位置关系可能是
b ∥ α,b与 α相交
b ∥ α,或b α,
或b与 α相交
(1)若两直线a、b异面,且 a ∥ α,则b与α的位置关系可能是
2.判断下列命题的真假
(1)过直线外一点只能引一条直线与
这条直线平行. ( )
(2)过平面外一点只能引一条直线与
这个平面平行. ( )
(3)若两条直线都和第三条直线垂直,
则这两条直线平行. ( )
(4)若两条直线都和第三条直线平行,
则这两条直线平行. ( )
真
假
真
假
例3:
分析
证法1
证法2
例3:证
明
证法1的思路是
线//线
线//面
线//线
线//面
证法2
利用相似三角形对应边成比例
及平行线分线段成比例的性质
∽
∽
(略写)
证法1
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
b
a
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
新课讲解
问题1:命题“若直线a平行于平面α,则直 线a平行于平面α内的一切直线.”对吗?
a
b
c
本节课研究的内容
?
b
a
?
证明:
新课:直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
?
b
a
?
注意:
1、定理三个条件缺一不可。
2、简记:线面平行,则线线平行。
例2:有一块木料如图,已知棱BC平行于面A′C′.
(1)要经过木料表面A′B′C′D′
内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC有什么关系?
演示课件
线//线
线//面
转化是立体几何的一种重要的思想方法
说明:
证明:
P62习题5
已知:如图,AB//平面 ,AC//BD,且 AC、BD与 分别相 交于点C, D.
求证:AC=BD
练习
小结
证明线面平行的
转化思想:
线//线
线//面
面//面
(1)平行公理
(2)三角形中位线
(3)平行线分线段成比例
(4)相似三角形对应边成比例
(5)平行四边形对边平行
练习
四、课堂练习:
(1)以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )
(2)如果直线a、b和平面α 满足a ∥ α,
b ∥ α,那么a ∥ b ;( )
(3)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α, 那么 b ∥ α;( )
(4)过平面外一点和这个平面平行的直线只有一条.( )
填空:
(2)若两直线a、b相交,且a ∥ α,则b与α的位置关系可能是
b ∥ α,b与 α相交
b ∥ α,或b α,
或b与 α相交
(1)若两直线a、b异面,且 a ∥ α,则b与α的位置关系可能是
2.判断下列命题的真假
(1)过直线外一点只能引一条直线与
这条直线平行. ( )
(2)过平面外一点只能引一条直线与
这个平面平行. ( )
(3)若两条直线都和第三条直线垂直,
则这两条直线平行. ( )
(4)若两条直线都和第三条直线平行,
则这两条直线平行. ( )
真
假
真
假
例3:
分析
证法1
证法2
例3:证
明
证法1的思路是
线//线
线//面
线//线
线//面
证法2
利用相似三角形对应边成比例
及平行线分线段成比例的性质
∽
∽
(略写)
证法1
