人教版高一上册数学课件《1.1.2循环结构框图》(18张PPT)
文档属性
| 名称 | 人教版高一上册数学课件《1.1.2循环结构框图》(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 16:45:07 | ||
图片预览





文档简介
算法与程序框图
第二课时
知识回忆
1、程序框图的概念
2、程序框图的图示和意义
3、顺序结构和条件结构的特点
4、作业分析
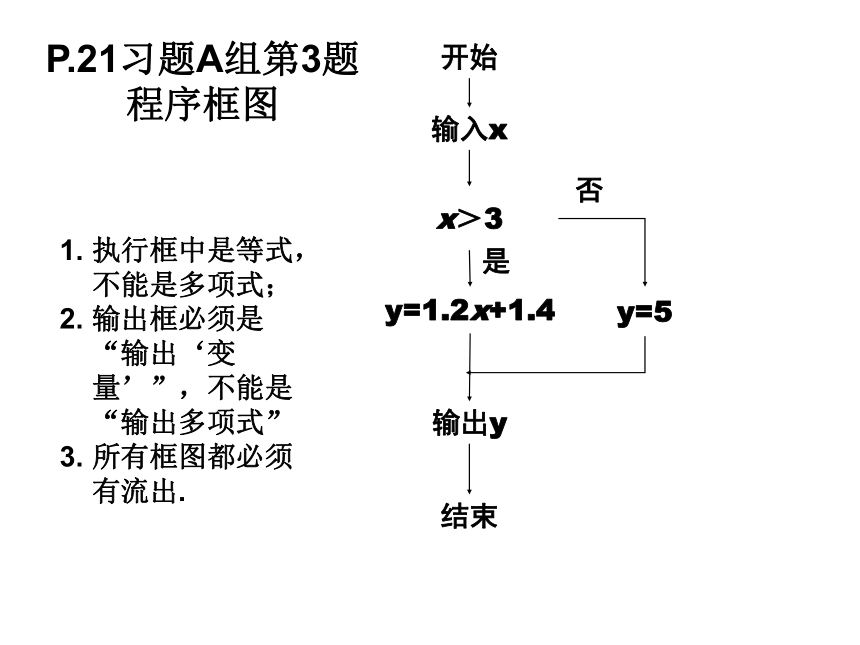
输入x
开始
x>3
y=1.2x+1.4
y=5
输出y
结束
否
是
P.21习题A组第3题
程序框图
执行框中是等式,不能是多项式;
输出框必须是“输出‘变量’”,不能是“输出多项式”
所有框图都必须有流出.
赋值语句
变量的值可以由输入的方式给定,也可以直接以赋值的方式给定。在算法中,我们可以根据需要改变变量的值,也就是说可以给变量重新赋值,取代原来的值。
形象的说,变量就像个盒子,可以装不同的数值,但是每次只能装一个,当放入新值,原来的值就会被取代。
赋值语句
a=1
b=2a+3
输出b
i=1
i=i+1
输出i
变量=表达式
顾名思义,赋值语句就是把表达式所代表的值赋给变量。语句中“=”叫赋值号,它和数学中的等号不完全一样。
计算机执行赋值语句时,先计算“=”右边的表达式的值,再把这个值赋给“=”左边的变量,如:
例2 交换两个变量A和B的值
算法
第一步:输入A,B,
第二步:令x=A,
第三步:令A=B,
第四步:令B=x,
第五步:输出A,B.
程序框图:
开始
B=x
输出A,B
结束
A=B
x=A
输入A,B
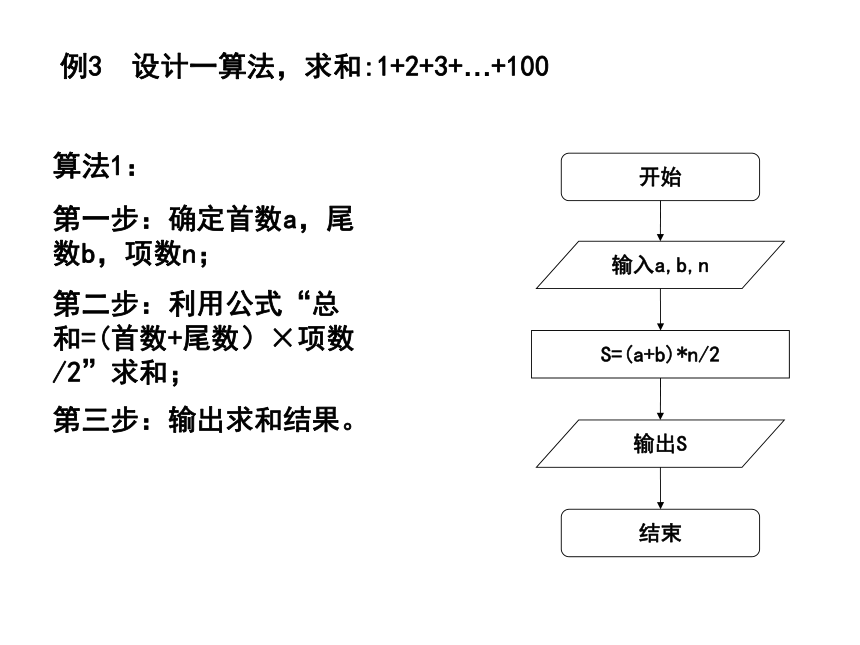
例3 设计一算法,求和:1+2+3+…+100
第一步:确定首数a,尾数b,项数n;
第二步:利用公式“总和=(首数+尾数)×项数/2”求和;
第三步:输出求和结果。
算法1:
开始
结束
输入a,b,n
S=(a+b)*n/2
输出S
例3 设计一算法,求和:1+2+3+…+100
算法2:
第一步:从1开始将自然数1、2、 3、…、100逐个相加;
第二步:输出累加结果。
思考:1、上边的式子有怎样的规律呢?
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
2、怎么用程序框图表示呢?
S=S + i
i = i + 1
4、如何使程序结束?
3、i有什么作用?S呢?
S=S + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
试分析两种流程的异同点
直到型结构
当型结构
S=S + i
i = i + 1
是
否
S=S + i
i = i + 1
否
是
i≤100?
i>100?
请填上判断的条件。
S=S + i
i = i + 1
最后的结果
结束
S=S + i
i = i + 1
i≤100?
输出S
否
是
i=1,S=0
开始
结束
输出S
i=1,S=0
开始
S=S + i
i = i + 1
i>100?
否
是
循环结构的三个要素:循环变量、循环体、循环终止条件。仿照下图你可以画出当型的流程图吗?
循环变量=初值
循环体
循环变量=循环变量的后继
循环变量>终值?
否
是
循环变量=初值
循环体
循环变量≤终值?
否
是
循环变量=循环变量的后继
步骤A
步骤B
思考:将步骤A和步骤B交换位置,结果会怎样?能达到预期结果吗?为什么?要达到预期结果,还需要做怎样的修改?
答:达不到预期结果;当i = 100时,退出循环,i的值未能加入到S中;修改的方法是将判断条件改为i<101
结束
S=S + i
i = i + 1
i≤100?
输出S
否
是
i=1,S=0
开始
练习巩固
1、设计一算法,求积:1×2×3×…×100,画出流程图
结束
输出S
i=1,S=1
开始
S=S*i
i = i + 1
i>100?
否
是
思考:该流程图与前面的例3中求和的流程图有何不同?
2、 对任意正整数n,
的值,并画出程序框图.
开始
输入正整数n
输出S
结束
S=0
i=1
S=S+1/i
i=i+1
i>n?
否
是
设计一个算法求
练习巩固
2、设计一算法输出1~1000以内能被3整除的整数
结束
i= i+1
i<1000?
输出i
否
是
i=0
开始
3整除i?
否
是
算法:
S1:确定i的初始值为0;
S2:判断i是否等于1000,若是则程序结束,否则进入S3;
S3:使i增加1,判断i是否能被3整除,若能输出i,并返回S2;否则直接返回S2
小结
1、循环结构的特点
2、循环结构的框图表示
3、循环结构有注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
课外作业
P21 习题1.1 A组 第2题
开始
S=0
I=I+1
I=1
S=S+I*I
I≤100
输出S
结束
N
Y
P21 A组 T2
作业答案
第二课时
知识回忆
1、程序框图的概念
2、程序框图的图示和意义
3、顺序结构和条件结构的特点
4、作业分析
输入x
开始
x>3
y=1.2x+1.4
y=5
输出y
结束
否
是
P.21习题A组第3题
程序框图
执行框中是等式,不能是多项式;
输出框必须是“输出‘变量’”,不能是“输出多项式”
所有框图都必须有流出.
赋值语句
变量的值可以由输入的方式给定,也可以直接以赋值的方式给定。在算法中,我们可以根据需要改变变量的值,也就是说可以给变量重新赋值,取代原来的值。
形象的说,变量就像个盒子,可以装不同的数值,但是每次只能装一个,当放入新值,原来的值就会被取代。
赋值语句
a=1
b=2a+3
输出b
i=1
i=i+1
输出i
变量=表达式
顾名思义,赋值语句就是把表达式所代表的值赋给变量。语句中“=”叫赋值号,它和数学中的等号不完全一样。
计算机执行赋值语句时,先计算“=”右边的表达式的值,再把这个值赋给“=”左边的变量,如:
例2 交换两个变量A和B的值
算法
第一步:输入A,B,
第二步:令x=A,
第三步:令A=B,
第四步:令B=x,
第五步:输出A,B.
程序框图:
开始
B=x
输出A,B
结束
A=B
x=A
输入A,B
例3 设计一算法,求和:1+2+3+…+100
第一步:确定首数a,尾数b,项数n;
第二步:利用公式“总和=(首数+尾数)×项数/2”求和;
第三步:输出求和结果。
算法1:
开始
结束
输入a,b,n
S=(a+b)*n/2
输出S
例3 设计一算法,求和:1+2+3+…+100
算法2:
第一步:从1开始将自然数1、2、 3、…、100逐个相加;
第二步:输出累加结果。
思考:1、上边的式子有怎样的规律呢?
S=0
S=S + 1
S=S + 2
S=S + 3
…
S=S + 100
2、怎么用程序框图表示呢?
S=S + i
i = i + 1
4、如何使程序结束?
3、i有什么作用?S呢?
S=S + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
试分析两种流程的异同点
直到型结构
当型结构
S=S + i
i = i + 1
是
否
S=S + i
i = i + 1
否
是
i≤100?
i>100?
请填上判断的条件。
S=S + i
i = i + 1
最后的结果
结束
S=S + i
i = i + 1
i≤100?
输出S
否
是
i=1,S=0
开始
结束
输出S
i=1,S=0
开始
S=S + i
i = i + 1
i>100?
否
是
循环结构的三个要素:循环变量、循环体、循环终止条件。仿照下图你可以画出当型的流程图吗?
循环变量=初值
循环体
循环变量=循环变量的后继
循环变量>终值?
否
是
循环变量=初值
循环体
循环变量≤终值?
否
是
循环变量=循环变量的后继
步骤A
步骤B
思考:将步骤A和步骤B交换位置,结果会怎样?能达到预期结果吗?为什么?要达到预期结果,还需要做怎样的修改?
答:达不到预期结果;当i = 100时,退出循环,i的值未能加入到S中;修改的方法是将判断条件改为i<101
结束
S=S + i
i = i + 1
i≤100?
输出S
否
是
i=1,S=0
开始
练习巩固
1、设计一算法,求积:1×2×3×…×100,画出流程图
结束
输出S
i=1,S=1
开始
S=S*i
i = i + 1
i>100?
否
是
思考:该流程图与前面的例3中求和的流程图有何不同?
2、 对任意正整数n,
的值,并画出程序框图.
开始
输入正整数n
输出S
结束
S=0
i=1
S=S+1/i
i=i+1
i>n?
否
是
设计一个算法求
练习巩固
2、设计一算法输出1~1000以内能被3整除的整数
结束
i= i+1
i<1000?
输出i
否
是
i=0
开始
3整除i?
否
是
算法:
S1:确定i的初始值为0;
S2:判断i是否等于1000,若是则程序结束,否则进入S3;
S3:使i增加1,判断i是否能被3整除,若能输出i,并返回S2;否则直接返回S2
小结
1、循环结构的特点
2、循环结构的框图表示
3、循环结构有注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
课外作业
P21 习题1.1 A组 第2题
开始
S=0
I=I+1
I=1
S=S+I*I
I≤100
输出S
结束
N
Y
P21 A组 T2
作业答案
