3.1.2函数的表示法 同步练习2021-2022学年高一上学期数学人教A版(2019)必修第一册第三章(Word含答解析)
文档属性
| 名称 | 3.1.2函数的表示法 同步练习2021-2022学年高一上学期数学人教A版(2019)必修第一册第三章(Word含答解析) |  | |
| 格式 | docx | ||
| 文件大小 | 116.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 17:36:59 | ||
图片预览




文档简介
3.1.2 函数的表示法
刷新题夯基础
题组一 函数的表示法及其应用
1.已知函数f(x)由下表给出,则f(11)= ( )
x
0≤x<5
5≤x<10
10≤x<15
15≤x≤20
f(x)
2
3
4
5
A.2 B.3 C.4 D.5
2.已知函数y=f(x)的对应关系如下表所示,函数y=g(x)的图象是如图所示的曲线ABC,则f[g(2)]的值为( )
5513070161925
x
1
2
3
f(x)
2
3
0
A.3 B.0 C.1 D.2
3.如图,李老师早晨出门锻炼,一段时间内沿半圆形路径M→A→C→B→M匀速慢跑一周,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是 ( )
题组二 函数解析式的求法
4.(2021河北衡水武邑中学高一上期中)已知f(x-1)=x2+4x-5,则f(x)= ( )
A.x2+6x B.x2+8x+7
C.x2+2x-3 D.x2+6x-10
5.已知fx+1x=x2+1x2+1x,则f(x)= ( )
A.x2-x+1,x≠0 B.x2+1x2+1x,x≠0
C.x2-x+1,x≠1 D.1+1x2+1x,x≠1
6.若f(x)对于任意实数x恒有3f(x)-2f(-x)=5x+1,则f(x)= ( )
A.x+1 B.x-1 C.2x+1 D.3x+3
7.已知f(x)是一次函数,2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)= . ?
8.某企业生产某种产品时的能耗y与所生产的产品件数x之间的关系式为y=ax+bx,其中,当x=2时,y=100;当x=7时,y=35,且此产品生产件数不超过20.则y关于x的解析式为 .?
题组三 分段函数问题的解法
9.(2021北京人大附中高一上期中)函数y=x2|x|的图象大致是 ( )
10.函数f(x)=2x2,0≤x<1,2,1≤x<2,3,x≥2的值域是 ( )
A.R B.[0,+∞) C.[0,3] D.[0,2]∪{3}
11.(2021北京房山高一上期中)为引导居民节约用电,某城市对居民生活用电实行“阶梯电价”,按月用电量计算,将居民家庭每月用电量划分为三个阶梯,电价按阶梯递增.第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时.若某户居民10月份交纳的电费为360元,则此户居民10月份的用电量为 千瓦时.?
12.(2020山东菏泽高一上期末)已知函数f(x)=x+5,x≤1,-2x+8,x>1.
(1)求f(2)及f[f(-1)]的值;
(2)解关于x的不等式f(x)≥4.
刷新题培素养
题组一 函数的表示法及其应用
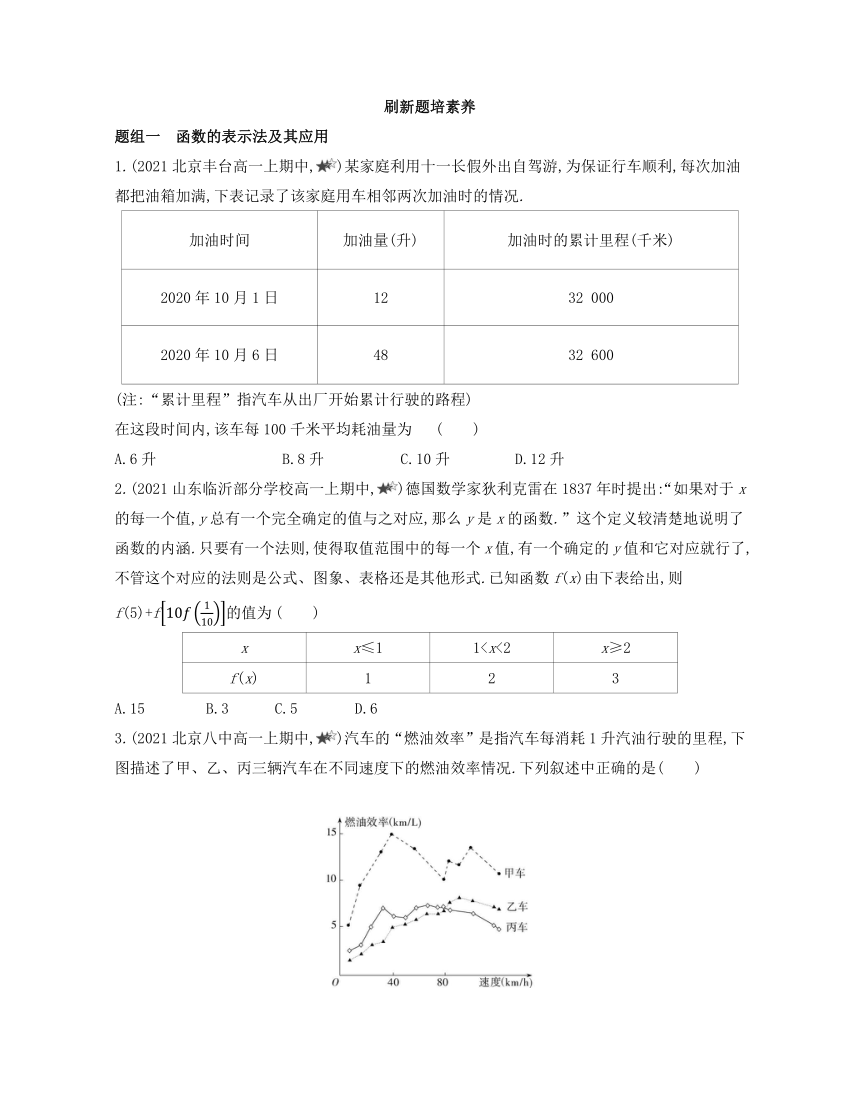
1.(2021北京丰台高一上期中,)某家庭利用十一长假外出自驾游,为保证行车顺利,每次加油都把油箱加满,下表记录了该家庭用车相邻两次加油时的情况.
加油时间
加油量(升)
加油时的累计里程(千米)
2020年10月1日
12
32 000
2020年10月6日
48
32 600
(注:“累计里程”指汽车从出厂开始累计行驶的路程)
在这段时间内,该车每100千米平均耗油量为 ( )
A.6升 B.8升 C.10升 D.12升
2.(2021山东临沂部分学校高一上期中,)德国数学家狄利克雷在1837年时提出:“如果对于x的每一个值,y总有一个完全确定的值与之对应,那么y是x的函数.”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个x值,有一个确定的y值和它对应就行了,不管这个对应的法则是公式、图象、表格还是其他形式.已知函数f(x)由下表给出,则f(5)+f10f110的值为 ( )
x
x≤1
1x≥2
f(x)
1
2
3
A.15 B.3 C.5 D.6
3.(2021北京八中高一上期中,)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/时,相同条件下,在该市用丙车比用乙车更省油
4.(2021北京交大附中高一上期中,)已知函数y=f(x),y=g(x)的对应关系如下表:
x
1
2
3
f(x)
1
3
1
x
1
2
3
g(x)
3
2
1
则f[g(1)]的值为 ;满足f[g(x)]>g[f(x)]的x的值为 .?
题组二 函数解析式的求法
5.()设函数f:R→R满足f(0)=1,且对任意x,y∈R,都有f(xy+1)=f(x)f(y)-f(y)-x+2,则f(2 019)= ( )
A.0 B.1 C.2 019 D.2 020
6.(2021浙江杭州高级中学高一上期中,)若函数f(x)满足关系式f(x)+2f(1-x)=-3x,则f(2)的值为 ( )
A.-32 B.32 C.-52 D.52
7.(多选)()已知f(2x+1)=x2,则下列结论正确的是 ( )
A.f(-3)=4 B.f(x)=x2-2x+14
C.f(x)=x2 D.f(3)=9
8.(2021山东滨州高一上期中,)已知函数f(2x-1)=3x-5,若f(x0)=4,则x0= .?
9.(2021山东菏泽一中等六校高一上第一次联考,)(1)已知f(x)=ax2+bx+c,若f(0)=2且f(x+1)=f(x)+2x+2,求f(x)的解析式;
(2)已知f(x)=x+2x,求f(x)的解析式.
题组三 分段函数问题的解法
10.(2021天津部分区高一上期中,)已知函数f(x)=x(x+4),x≥0,x(x-4),x<0,若f(a)≤5,则实数a的取值范围是 ( )
A.[-1,1] B.[-5,5] C.(-∞,-1]∪[1,+∞) D.(-∞,-5]∪[5,+∞)
11.(多选)()已知函数f(x)=x+2,x≤-1,x2,-1A. f(x)的值域为(-∞,4) B. f(1)=3
C.若f(x)=3,则x的值是3 D. f(x)<1的解集为(-1,1)
12.(多选)(2021江苏南通如东高一上期中,)在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间并构成了一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer),简单地讲就是对于满足一定条件的连续函数f(x),如果存在一个点x0,使得f(x0)=x0,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是 ( )
A. f(x)=1x+x B.g(x)=x2-x-3
C. f(x)=2x2-1,x≤1|2-x|,x>1 D.f(x)=1x-x
13.(2021河北衡水武邑中学高一上期中,)已知f(x)=x-5(x≥7),f(x+4)(x<7)(x∈N),那么f(3)= .?
14.(2021山东省实验中学高一上期中,)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表
低谷时间段用电价格表
高峰月用电量
(单位:千瓦时)
高峰电价
(单位:元/千瓦时)
低谷月用电量
(单位:千瓦时)
低谷电价
(单位:元/千瓦时)
50及以下
的部分
0.568
50及以下
的部分
0.288
超过50但不
超过200的部分
0.598
超过50但不
超过200的部分
0.318
超过200的部分
0.668
超过200的部分
0.388
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭5月份应付的电费为 元(用数字作答).?
15. (2020北京人大附中高一上期中,)已知函数f(x)=x+2,x≤0,-x+2,x>0,则方程f(x)=x2的解集为 .?
16.()函数y=f(x)的图象如图所示.
(1)求函数y=f(x)的定义域;
(2)求函数y=f(x)的值域;
(3)y为何值时,只有唯一的x值与之对应?
48933106350
17.(2020北京通州高一上期末,)下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯
户年用水量
(立方米)
水价
其中
自来
水费
水资
源费
污水处
理费
第一阶梯
0~180(含)
5.00
2.07
1.57
1.36
第二阶梯
180~260(含)
7.00
4.07
第三阶梯
260以上
9.00
6.07
(1)试写出水费y(元)与年用水量x(立方米)之间的函数解析式;
(2)若某户居民一年交水费1 040元,求其中自来水费、水资源费及污水处理费各是多少.
答案全解全析
刷新题夯基础
1.C 由题表可知f(11)=4.
2.D 由题图可知g(2)=1,由题表可知f(1)=2,
故f[g(2)]=2.故选D.
3.D 由题意得,从M到A的过程中,李老师与M的距离在增大,由A经C到B的过程中,李老师与M的距离不变,都是半圆的半径长,由B到M的过程中,李老师与M的距离逐渐减小,故选D.
4.A 令x-1=t,则x=t+1,
∵f(x-1)=x2+4x-5,
∴f(t)=(t+1)2+4(t+1)-5=t2+6t,
由此可得f(x)=x2+6x.故选A.
5.C 设x+1x=t,则x=1t-1,t≠1,
则f(t)=1t-12+11t-12+t-1=t2-t+1,t≠1.
所以f(x)=x2-x+1,x≠1.故选C.
6.A 因为3f(x)-2f(-x)=5x+1,所以3f(-x)-2f(x)=-5x+1,解得f(x)=x+1.故选A.
7.答案 3x-2
解析 设f(x)=kx+b(k≠0),则2(2k+b)-3(k+b)=5,2b-(-k+b)=1,整理得k-b=5,k+b=1,
解得k=3,b=-2,所以f(x)=3x-2.
8.答案 y=x+196x(0解析 由题意知2a+b2=100,7a+b7=35,
即4a+b=200,49a+b=245,解得a=1,b=196,
所以所求函数的解析式为y=x+196x(09.A 因为y=x2|x|,所以定义域为{x|x≠0},所以y=x2|x|=x,x>0,-x,x<0.其函数图象如A中所示.故选A.
10.D 当x∈[0,1)时, f(x)∈[0,2);
当x∈[1,2)时, f(x)∈{2};
当x∈[2,+∞)时, f(x)∈{3}.
所以f(x)的值域为[0,2]∪{3}.
11.答案 580
信息提取 ①居民家庭每月用电量划分为三个阶梯,电价按阶梯递增;②第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时;③某户居民10月份交纳的电费为360元.
数学建模 以生活中的“阶梯电价”为背景,构造分段函数,利用分段函数解决问题.
解析 设某户居民一个月的用电量为x千瓦时,电费为f(x)元,则当0≤x≤240时, f(x)=0.5x;当240400时, f(x)=0.5×240+0.6×160+0.8×(x-400)=0.8x-104.
故f(x)=0.5x(0≤x≤240),0.6x-24(240400),
根据10月份此户居民交纳的电费可知,此户居民用到了第三阶梯电量,
令0.8x-104=360,得x=580.
所以此户居民10月份的用电量为580千瓦时.
12.解析 (1)f(2)=-2×2+8=4,
f[f(-1)]=f(-1+5)=f(4)=-2×4+8=0.
(2)当x≤1时,由f(x)≥4得x+5≥4,即x≥-1,此时-1≤x≤1;
当x>1时,由f(x)≥4得-2x+8≥4,即x≤2,此时1综上,不等式的解集为[-1,2].
刷新题培素养
1.B 由题表中的信息可知,2020年10月1日油箱加满了油,此时的累计里程为32 000千米,到2020年10月6日,油箱加满油需要48升,说明这段时间的耗油量为48升,累计里程为32 600千米,说明这段时间内汽车行驶了600千米,
则在这段时间内,该车每100千米平均耗油量为486=8升.故选B.
2.D 由题表得f(5)=3, f110=1,
∴f10f110=f(10)=3,
∴f(5)+f10f110=3+3=6.
故选D.
3.D 对于A选项,由题图可知,当乙车速度大于40千米/时 时,乙车每消耗1升汽油,行驶里程都超过5千米,故A错;
对于B选项,由题意可知,以相同速度行驶相同里程,燃油效率越高,耗油越少,故三辆车中甲车耗油最少,故B错;
对于C选项,甲车以80千米/时的速度行驶时,燃油效率为10 km/L,则行驶1小时,消耗汽油80×1÷10=8(升),故C错;
对于选项D,当行驶速度小于80千米/时时,在相同条件下,丙车的燃油效率高于乙车,则在该城市用丙车比用乙车更省油,故D对.故选D.
4.答案 1;2
解析 g(1)=3,则f[g(1)]=f(3)=1.
当x=1时, f[g(1)]=1,g[f(1)]=g(1)=3,不满足f[g(x)]>g[f(x)],
当x=2时, f[g(2)]=f(2)=3,g[f(2)]=g(3)=1,满足f[g(x)]>g[f(x)],
当x=3时, f[g(3)]=f(1)=1,g[f(3)]=g(1)=3,不满足f[g(x)]>g[f(x)],
故满足f[g(x)]>g[f(x)]的x的值为2.
5.D f(xy+1)=f(x)f(y)-f(y)-x+2, f(0)=1,
当x=0时, f(1)=f(0)f(y)-f(y)+2=2,
当y=0时, f(1)=f(x)f(0)-f(0)-x+2=2,因此f(x)=x+1,
所以f(2 019)=2 020,故选D.
6.D ∵f(x)+2f(1-x)=-3x,①
∴f(1-x)+2f(x)=-31-x,②
②×2-①得3f(x)=6x-1+3x.
因此, f(x)=2x-1+1x,
∴f(2)=22-1+12=52.故选D.
7.AB f(2x+1)=x2,令t=2x+1,则x=t-12,
所以f(t)=t-122=t2-2t+14,
则f(x)=x2-2x+14,故B正确,C错误;
f(-3)=(-3)2-2×(-3)+14=4,故A正确;
f(3)=32-2×3+14=1,故D错误.故选AB.
8.答案 5
解析 f(2x-1)=3x-5,令2x-1=t,则x=t+12,
则f(t)=3(t+1)2-5=3t-72,∴f(x)=3x-72,
∵f(x0)=4,∴3x0-72=4,解得x0=5.
故答案为5.
9.解析 (1)由f(0)=2,得c=2,
∴f(x)=ax2+bx+2,又f(x+1)=f(x)+2x+2,
∴ax2+(2a+b)x+a+b+2=ax2+(b+2)x+4,
∴2a+b=b+2,a+b+2=4,解得a=1,b=1.
∴f(x)=x2+x+2.
(2)令t=x,则t≥0,∴f(t)=t2+2t,t≥0,∴f(x)=x2+2x,x≥0.
10.A ∵f(a)≤5,∴a≥0,a2+4a-5≤0或a<0,a2-4a-5≤0,
即a≥0,-5≤a≤1或a<0,-1≤a≤5,
∴0≤a≤1或-1≤a<0,即-1≤a≤1.
故a的取值范围是[-1,1],故选A.
11.AC 当x≤-1时, f(x)的取值范围是(-∞,1],当-112.BCD 对于选项A,当1x0+x0=x0时,1x0=0,方程无解,所以函数f(x)=1x+x不是“不动点”函数;对于选项B,当x02-x0-3=x0时,解得x0=3或x0=-1,所以函数g(x)=x2-x-3是“不动点”函数;对于选项C,当x0≤1时,2x02-1=x0,解得x0=1或x0=-12;当x0>1时,|2-x0|=x0,解得x0=1(舍去),所以函数f(x)=2x2-1,x≤1,|2-x|,x>1是“不动点”函数;对于选项D,当1x0-x0=x0时,解得x0=±22,所以函数f(x)=1x-x是“不动点”函数.故选BCD.
13.答案 2
解析 ∵f(x)=x-5(x≥7),f(x+4)(x<7)(x∈N),∴f(3)=f(7)=7-5=2.
14.答案 148.4
解析 高峰时间段的电费为50×0.568+150×0.598=28.4+89.7=118.1(元),
低谷时间段的电费为50×0.288+50×0.318=14.4+15.9=30.3(元),
故该家庭5月份的总电费为118.1+30.3=148.4(元).
15.答案 {-1,1}
解析 方程f(x)=x2等价于x≤0,x+2=x2或x>0,-x+2=x2,解得x=-1或x=1,因此方程f(x)=x2的解集为{-1,1}.
16.解析 (1)由题图知函数y=f(x)的定义域为[-3,0]∪[1,4].
(2)由题图知函数y=f(x)的值域为[-2,2].
(3)由题图知,当y∈(0,2]时,只有唯一的x值与之对应.
17.信息提取 ①水价包括三部分:自来水费、水资源费、污水处理费;②自来水费按三阶收费,第一阶梯:用水量0~180(含),自来水费2.07元/立方米,第二阶梯:用水量180~260(含),自来水费4.07元/立方米,第三阶梯:用水量260以上,自来水费6.07元/立方米.
数学建模 以北京市居民用水实行阶梯水价为实际背景,构造函数模型,应用函数模型解决
问题.
解析 (1)依题意得y=5x,0≤x≤180,7(x-180)+900,180260,
即y=5x,0≤x≤180,7x-360,180260.
(2)依题意得y=1 040,
若x∈[0,180],则5x=1 040,解得x=208,不合题意,舍去;
若x∈(180,260],则7x-360=1 040,解得x=200,符合题意;
若x>260,则9x-880>1 040,不合题意.
故该用户当年用水量为200立方米.
因此,自来水费为2.07×180+4.07×20=454(元),水资源费为1.57×200=314(元),污水处理费为1.36×200=272(元).
解题模板 利用函数解决应用问题时,要准确分析问题中的量及它们之间的关系,存在不同的函数关系时可利用分段函数求解.
刷新题夯基础
题组一 函数的表示法及其应用
1.已知函数f(x)由下表给出,则f(11)= ( )
x
0≤x<5
5≤x<10
10≤x<15
15≤x≤20
f(x)
2
3
4
5
A.2 B.3 C.4 D.5
2.已知函数y=f(x)的对应关系如下表所示,函数y=g(x)的图象是如图所示的曲线ABC,则f[g(2)]的值为( )
5513070161925
x
1
2
3
f(x)
2
3
0
A.3 B.0 C.1 D.2
3.如图,李老师早晨出门锻炼,一段时间内沿半圆形路径M→A→C→B→M匀速慢跑一周,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是 ( )
题组二 函数解析式的求法
4.(2021河北衡水武邑中学高一上期中)已知f(x-1)=x2+4x-5,则f(x)= ( )
A.x2+6x B.x2+8x+7
C.x2+2x-3 D.x2+6x-10
5.已知fx+1x=x2+1x2+1x,则f(x)= ( )
A.x2-x+1,x≠0 B.x2+1x2+1x,x≠0
C.x2-x+1,x≠1 D.1+1x2+1x,x≠1
6.若f(x)对于任意实数x恒有3f(x)-2f(-x)=5x+1,则f(x)= ( )
A.x+1 B.x-1 C.2x+1 D.3x+3
7.已知f(x)是一次函数,2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)= . ?
8.某企业生产某种产品时的能耗y与所生产的产品件数x之间的关系式为y=ax+bx,其中,当x=2时,y=100;当x=7时,y=35,且此产品生产件数不超过20.则y关于x的解析式为 .?
题组三 分段函数问题的解法
9.(2021北京人大附中高一上期中)函数y=x2|x|的图象大致是 ( )
10.函数f(x)=2x2,0≤x<1,2,1≤x<2,3,x≥2的值域是 ( )
A.R B.[0,+∞) C.[0,3] D.[0,2]∪{3}
11.(2021北京房山高一上期中)为引导居民节约用电,某城市对居民生活用电实行“阶梯电价”,按月用电量计算,将居民家庭每月用电量划分为三个阶梯,电价按阶梯递增.第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时.若某户居民10月份交纳的电费为360元,则此户居民10月份的用电量为 千瓦时.?
12.(2020山东菏泽高一上期末)已知函数f(x)=x+5,x≤1,-2x+8,x>1.
(1)求f(2)及f[f(-1)]的值;
(2)解关于x的不等式f(x)≥4.
刷新题培素养
题组一 函数的表示法及其应用
1.(2021北京丰台高一上期中,)某家庭利用十一长假外出自驾游,为保证行车顺利,每次加油都把油箱加满,下表记录了该家庭用车相邻两次加油时的情况.
加油时间
加油量(升)
加油时的累计里程(千米)
2020年10月1日
12
32 000
2020年10月6日
48
32 600
(注:“累计里程”指汽车从出厂开始累计行驶的路程)
在这段时间内,该车每100千米平均耗油量为 ( )
A.6升 B.8升 C.10升 D.12升
2.(2021山东临沂部分学校高一上期中,)德国数学家狄利克雷在1837年时提出:“如果对于x的每一个值,y总有一个完全确定的值与之对应,那么y是x的函数.”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个x值,有一个确定的y值和它对应就行了,不管这个对应的法则是公式、图象、表格还是其他形式.已知函数f(x)由下表给出,则f(5)+f10f110的值为 ( )
x
x≤1
1
f(x)
1
2
3
A.15 B.3 C.5 D.6
3.(2021北京八中高一上期中,)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/时,相同条件下,在该市用丙车比用乙车更省油
4.(2021北京交大附中高一上期中,)已知函数y=f(x),y=g(x)的对应关系如下表:
x
1
2
3
f(x)
1
3
1
x
1
2
3
g(x)
3
2
1
则f[g(1)]的值为 ;满足f[g(x)]>g[f(x)]的x的值为 .?
题组二 函数解析式的求法
5.()设函数f:R→R满足f(0)=1,且对任意x,y∈R,都有f(xy+1)=f(x)f(y)-f(y)-x+2,则f(2 019)= ( )
A.0 B.1 C.2 019 D.2 020
6.(2021浙江杭州高级中学高一上期中,)若函数f(x)满足关系式f(x)+2f(1-x)=-3x,则f(2)的值为 ( )
A.-32 B.32 C.-52 D.52
7.(多选)()已知f(2x+1)=x2,则下列结论正确的是 ( )
A.f(-3)=4 B.f(x)=x2-2x+14
C.f(x)=x2 D.f(3)=9
8.(2021山东滨州高一上期中,)已知函数f(2x-1)=3x-5,若f(x0)=4,则x0= .?
9.(2021山东菏泽一中等六校高一上第一次联考,)(1)已知f(x)=ax2+bx+c,若f(0)=2且f(x+1)=f(x)+2x+2,求f(x)的解析式;
(2)已知f(x)=x+2x,求f(x)的解析式.
题组三 分段函数问题的解法
10.(2021天津部分区高一上期中,)已知函数f(x)=x(x+4),x≥0,x(x-4),x<0,若f(a)≤5,则实数a的取值范围是 ( )
A.[-1,1] B.[-5,5] C.(-∞,-1]∪[1,+∞) D.(-∞,-5]∪[5,+∞)
11.(多选)()已知函数f(x)=x+2,x≤-1,x2,-1
C.若f(x)=3,则x的值是3 D. f(x)<1的解集为(-1,1)
12.(多选)(2021江苏南通如东高一上期中,)在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间并构成了一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer),简单地讲就是对于满足一定条件的连续函数f(x),如果存在一个点x0,使得f(x0)=x0,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是 ( )
A. f(x)=1x+x B.g(x)=x2-x-3
C. f(x)=2x2-1,x≤1|2-x|,x>1 D.f(x)=1x-x
13.(2021河北衡水武邑中学高一上期中,)已知f(x)=x-5(x≥7),f(x+4)(x<7)(x∈N),那么f(3)= .?
14.(2021山东省实验中学高一上期中,)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表
低谷时间段用电价格表
高峰月用电量
(单位:千瓦时)
高峰电价
(单位:元/千瓦时)
低谷月用电量
(单位:千瓦时)
低谷电价
(单位:元/千瓦时)
50及以下
的部分
0.568
50及以下
的部分
0.288
超过50但不
超过200的部分
0.598
超过50但不
超过200的部分
0.318
超过200的部分
0.668
超过200的部分
0.388
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭5月份应付的电费为 元(用数字作答).?
15. (2020北京人大附中高一上期中,)已知函数f(x)=x+2,x≤0,-x+2,x>0,则方程f(x)=x2的解集为 .?
16.()函数y=f(x)的图象如图所示.
(1)求函数y=f(x)的定义域;
(2)求函数y=f(x)的值域;
(3)y为何值时,只有唯一的x值与之对应?
48933106350
17.(2020北京通州高一上期末,)下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯
户年用水量
(立方米)
水价
其中
自来
水费
水资
源费
污水处
理费
第一阶梯
0~180(含)
5.00
2.07
1.57
1.36
第二阶梯
180~260(含)
7.00
4.07
第三阶梯
260以上
9.00
6.07
(1)试写出水费y(元)与年用水量x(立方米)之间的函数解析式;
(2)若某户居民一年交水费1 040元,求其中自来水费、水资源费及污水处理费各是多少.
答案全解全析
刷新题夯基础
1.C 由题表可知f(11)=4.
2.D 由题图可知g(2)=1,由题表可知f(1)=2,
故f[g(2)]=2.故选D.
3.D 由题意得,从M到A的过程中,李老师与M的距离在增大,由A经C到B的过程中,李老师与M的距离不变,都是半圆的半径长,由B到M的过程中,李老师与M的距离逐渐减小,故选D.
4.A 令x-1=t,则x=t+1,
∵f(x-1)=x2+4x-5,
∴f(t)=(t+1)2+4(t+1)-5=t2+6t,
由此可得f(x)=x2+6x.故选A.
5.C 设x+1x=t,则x=1t-1,t≠1,
则f(t)=1t-12+11t-12+t-1=t2-t+1,t≠1.
所以f(x)=x2-x+1,x≠1.故选C.
6.A 因为3f(x)-2f(-x)=5x+1,所以3f(-x)-2f(x)=-5x+1,解得f(x)=x+1.故选A.
7.答案 3x-2
解析 设f(x)=kx+b(k≠0),则2(2k+b)-3(k+b)=5,2b-(-k+b)=1,整理得k-b=5,k+b=1,
解得k=3,b=-2,所以f(x)=3x-2.
8.答案 y=x+196x(0
即4a+b=200,49a+b=245,解得a=1,b=196,
所以所求函数的解析式为y=x+196x(0
10.D 当x∈[0,1)时, f(x)∈[0,2);
当x∈[1,2)时, f(x)∈{2};
当x∈[2,+∞)时, f(x)∈{3}.
所以f(x)的值域为[0,2]∪{3}.
11.答案 580
信息提取 ①居民家庭每月用电量划分为三个阶梯,电价按阶梯递增;②第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时;③某户居民10月份交纳的电费为360元.
数学建模 以生活中的“阶梯电价”为背景,构造分段函数,利用分段函数解决问题.
解析 设某户居民一个月的用电量为x千瓦时,电费为f(x)元,则当0≤x≤240时, f(x)=0.5x;当240
故f(x)=0.5x(0≤x≤240),0.6x-24(240
根据10月份此户居民交纳的电费可知,此户居民用到了第三阶梯电量,
令0.8x-104=360,得x=580.
所以此户居民10月份的用电量为580千瓦时.
12.解析 (1)f(2)=-2×2+8=4,
f[f(-1)]=f(-1+5)=f(4)=-2×4+8=0.
(2)当x≤1时,由f(x)≥4得x+5≥4,即x≥-1,此时-1≤x≤1;
当x>1时,由f(x)≥4得-2x+8≥4,即x≤2,此时1
刷新题培素养
1.B 由题表中的信息可知,2020年10月1日油箱加满了油,此时的累计里程为32 000千米,到2020年10月6日,油箱加满油需要48升,说明这段时间的耗油量为48升,累计里程为32 600千米,说明这段时间内汽车行驶了600千米,
则在这段时间内,该车每100千米平均耗油量为486=8升.故选B.
2.D 由题表得f(5)=3, f110=1,
∴f10f110=f(10)=3,
∴f(5)+f10f110=3+3=6.
故选D.
3.D 对于A选项,由题图可知,当乙车速度大于40千米/时 时,乙车每消耗1升汽油,行驶里程都超过5千米,故A错;
对于B选项,由题意可知,以相同速度行驶相同里程,燃油效率越高,耗油越少,故三辆车中甲车耗油最少,故B错;
对于C选项,甲车以80千米/时的速度行驶时,燃油效率为10 km/L,则行驶1小时,消耗汽油80×1÷10=8(升),故C错;
对于选项D,当行驶速度小于80千米/时时,在相同条件下,丙车的燃油效率高于乙车,则在该城市用丙车比用乙车更省油,故D对.故选D.
4.答案 1;2
解析 g(1)=3,则f[g(1)]=f(3)=1.
当x=1时, f[g(1)]=1,g[f(1)]=g(1)=3,不满足f[g(x)]>g[f(x)],
当x=2时, f[g(2)]=f(2)=3,g[f(2)]=g(3)=1,满足f[g(x)]>g[f(x)],
当x=3时, f[g(3)]=f(1)=1,g[f(3)]=g(1)=3,不满足f[g(x)]>g[f(x)],
故满足f[g(x)]>g[f(x)]的x的值为2.
5.D f(xy+1)=f(x)f(y)-f(y)-x+2, f(0)=1,
当x=0时, f(1)=f(0)f(y)-f(y)+2=2,
当y=0时, f(1)=f(x)f(0)-f(0)-x+2=2,因此f(x)=x+1,
所以f(2 019)=2 020,故选D.
6.D ∵f(x)+2f(1-x)=-3x,①
∴f(1-x)+2f(x)=-31-x,②
②×2-①得3f(x)=6x-1+3x.
因此, f(x)=2x-1+1x,
∴f(2)=22-1+12=52.故选D.
7.AB f(2x+1)=x2,令t=2x+1,则x=t-12,
所以f(t)=t-122=t2-2t+14,
则f(x)=x2-2x+14,故B正确,C错误;
f(-3)=(-3)2-2×(-3)+14=4,故A正确;
f(3)=32-2×3+14=1,故D错误.故选AB.
8.答案 5
解析 f(2x-1)=3x-5,令2x-1=t,则x=t+12,
则f(t)=3(t+1)2-5=3t-72,∴f(x)=3x-72,
∵f(x0)=4,∴3x0-72=4,解得x0=5.
故答案为5.
9.解析 (1)由f(0)=2,得c=2,
∴f(x)=ax2+bx+2,又f(x+1)=f(x)+2x+2,
∴ax2+(2a+b)x+a+b+2=ax2+(b+2)x+4,
∴2a+b=b+2,a+b+2=4,解得a=1,b=1.
∴f(x)=x2+x+2.
(2)令t=x,则t≥0,∴f(t)=t2+2t,t≥0,∴f(x)=x2+2x,x≥0.
10.A ∵f(a)≤5,∴a≥0,a2+4a-5≤0或a<0,a2-4a-5≤0,
即a≥0,-5≤a≤1或a<0,-1≤a≤5,
∴0≤a≤1或-1≤a<0,即-1≤a≤1.
故a的取值范围是[-1,1],故选A.
11.AC 当x≤-1时, f(x)的取值范围是(-∞,1],当-1
13.答案 2
解析 ∵f(x)=x-5(x≥7),f(x+4)(x<7)(x∈N),∴f(3)=f(7)=7-5=2.
14.答案 148.4
解析 高峰时间段的电费为50×0.568+150×0.598=28.4+89.7=118.1(元),
低谷时间段的电费为50×0.288+50×0.318=14.4+15.9=30.3(元),
故该家庭5月份的总电费为118.1+30.3=148.4(元).
15.答案 {-1,1}
解析 方程f(x)=x2等价于x≤0,x+2=x2或x>0,-x+2=x2,解得x=-1或x=1,因此方程f(x)=x2的解集为{-1,1}.
16.解析 (1)由题图知函数y=f(x)的定义域为[-3,0]∪[1,4].
(2)由题图知函数y=f(x)的值域为[-2,2].
(3)由题图知,当y∈(0,2]时,只有唯一的x值与之对应.
17.信息提取 ①水价包括三部分:自来水费、水资源费、污水处理费;②自来水费按三阶收费,第一阶梯:用水量0~180(含),自来水费2.07元/立方米,第二阶梯:用水量180~260(含),自来水费4.07元/立方米,第三阶梯:用水量260以上,自来水费6.07元/立方米.
数学建模 以北京市居民用水实行阶梯水价为实际背景,构造函数模型,应用函数模型解决
问题.
解析 (1)依题意得y=5x,0≤x≤180,7(x-180)+900,180
即y=5x,0≤x≤180,7x-360,180
(2)依题意得y=1 040,
若x∈[0,180],则5x=1 040,解得x=208,不合题意,舍去;
若x∈(180,260],则7x-360=1 040,解得x=200,符合题意;
若x>260,则9x-880>1 040,不合题意.
故该用户当年用水量为200立方米.
因此,自来水费为2.07×180+4.07×20=454(元),水资源费为1.57×200=314(元),污水处理费为1.36×200=272(元).
解题模板 利用函数解决应用问题时,要准确分析问题中的量及它们之间的关系,存在不同的函数关系时可利用分段函数求解.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
