2022届四川省内江市高中零模(高二期末)考试数学(文)试题(PDF版)含答案
文档属性
| 名称 | 2022届四川省内江市高中零模(高二期末)考试数学(文)试题(PDF版)含答案 |

|
|
| 格式 | |||
| 文件大小 | 331.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览


文档简介
内 江 市 高 中 2022 届 零 模 试 题
数 学 (文 科 )
本 试 卷 共 4 页 ,全 卷 满 分 150 分 ,考 试 时 间 120 分 钟 。
注 意 事 项 :
1.答 题 前 ,考 生 务 必 将 自 己 的 姓 名 、考 号 、班 级 用 签 字 笔 填 写 在 答 题 卡 相 应 位 置 .
2.选 择 题 选 出 答 案 后 ,用 铅 笔 把 答 题 卡 上 对 应 题 目 的 答 案 标 号 涂 黑 。如 需 改 动 ,用 橡 皮 擦
干 净 后 ,再 选 涂 其 它 答 案 。不 能 答 在 试 题 卷 上 。
3.非 选 择 题 用 签 字 笔 将 答 案 直 接 答 在 答 题 卡 相 应 位 置 上 。
4.考 试 结 束 后 ,监 考 人 员 将 答 题 卡 收 回 。
一 、选 择 题 :(本 大 题 共 12 个 小 题 ,每 小 题 5 分 ,共 60 分 .在 每 小 题 的 四 个 选 项 中 只 有 一 个
是 正 确 的 ,把 正 确 选 项 的 代 号 填 涂 在 答 题 卡 的 指 定 位 置 上 .)
1.复 数 z满 足 z(1 -i)=i(i为 虚 数 单 位 ),则 z的 虚 部 为
1 1 1 1
A. - B. C. i D. - i
2 2 2 2
π
2.设 f(x)=xcosx,则 f′( =
2 )
π π
A. B. - C.1 D. -1
2 2
2 2
3.若 双 曲 线 mx -y =1(m>0)的 离 心 率 为 2,则 m=
1 1
A. B. 3 C. 3 D.3
3 槡 3 或
x
4.设 命 题 p:函 数 f(x)=2 在 R上 为 单 调 递 增 函 数 ;命 题 q:函 数 f(x)=cos2x 为 奇 函 数 ,
则 下 列 命 题 中 真 命 题 是
A.p∧ q B.(? p)∧ (? q) C.(? p)∨ q D.p∧ (? q)
5.曲 线 y=f(x)在 x=1 处 的 切 线 如 图 所 示 ,则 f′(1)-f(1)=
A.0 B.2
C. -2 D. -1
2 2
x y
6.以 椭 圆 C:2 + 2 =1 a>b>0
a b ( )的 短 轴 的 一 个 端 点 和 两 焦 点 为
顶 点 的 三 角 形 为 等 边 三 角 形 ,且 椭 圆 C上 的 点 到 左 焦 点 的 最 大 距 离 为 6,则 椭 圆 C的 标 准 方 程
为
2 2 2 2
x y x y
A. + =1 B. + =1
4 3 8 4
2 2 2 2
x y x y
C. + =1 D. + =1
16 12 64 48
7.对 于 下 表 格 中 的 数 据 进 行 回 归 分 析 时 ,下 列 四 个 函 数 模 型 拟 合 效 果 最 优 的 是
x 1 2 3
y 3 5.99 12.01
x-1 2
A.y=3 ×2 B.y=log2x C.y=3x D.y=x
高 二 数 学 (文 科 )试 卷 第 1页 (共 4 页 )
x
8.已 知 函 数 f(x)=e -ax,则 “a<0”是 “函 数 f(x)为 增 函 数 ”的
A.充 分 不 必 要 条 件 B.必 要 不 充 分 条 件
C.充 要 条 件 D.既 不 充 分 也 不 必 要 条 件
9.“二 进 制 ”来 源 于 我 国 古 代 的 《易 经 》,二 进 制 数 由 数 字 0 和 1 组 成 ,比 如 :二 进 制 数
2 1 0
011(2)化 为 十 进 制 的 计 算 公 式 如 下 :011(2)=0 ×2 +1 ×2 +1 ×2 =3(10).若 从 二 进 制 数 11(2)、
00(2)、10(2)、01(2)中 任 选 一 个 数 字 ,则 二 进 制 数 所 对 应 的 十 进 制 数 大 于 2 的 概 率 为
1 1 2 1
A. B. C. D.
2 3 3 4
10.空 气 质 量 指 数 AQI是 反 映 空 气 质 量 状 况 的 指 数 ,其 对 应 关 系 如 下 表 :
AQI指 数 值 0 ~50 51 ~100 101 ~150 151 ~200 201 ~300 >300
空 气 质 量 优 良 轻 度 污 染 中 度 污 染 重 度 污 染 严 重 污 染
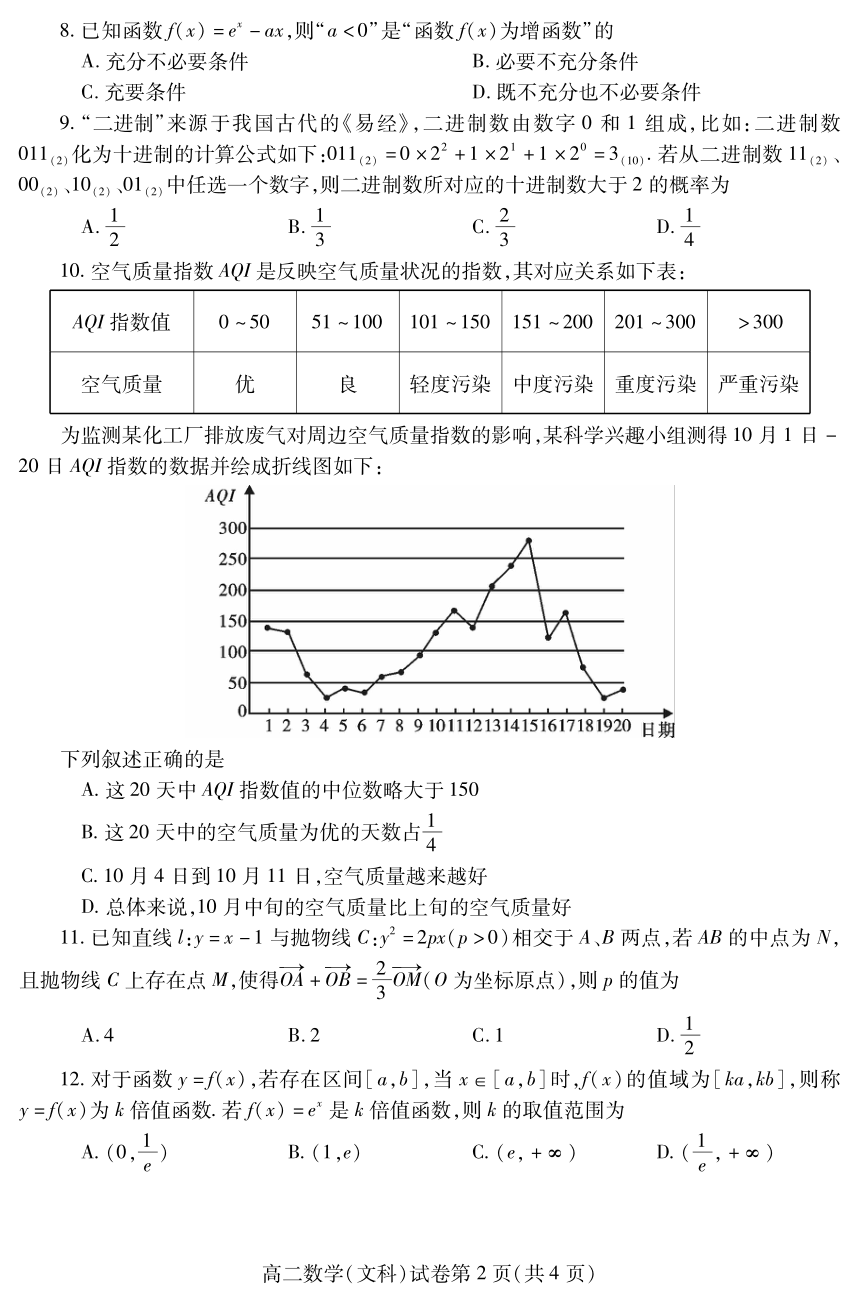
为 监 测 某 化 工 厂 排 放 废 气 对 周 边 空 气 质 量 指 数 的 影 响 ,某 科 学 兴 趣 小 组 测 得 10 月 1 日 -
20 日 AQI指 数 的 数 据 并 绘 成 折 线 图 如 下 :
下 列 叙 述 正 确 的 是
A.这 20 天 中 AQI指 数 值 的 中 位 数 略 大 于 150
1
B.这 20 天 中 的 空 气 质 量 为 优 的 天 数 占 4
C.10 月 4 日 到 10 月 11 日 ,空 气 质 量 越 来 越 好
D.总 体 来 说 ,10 月 中 旬 的 空 气 质 量 比 上 旬 的 空 气 质 量 好
2
11.已 知 直 线 l:y=x-1 与 抛 物 线 C:y =2px(p>0)相 交 于 A、B 两 点 ,若 AB 的 中 点 为 N,
??→ ?? → 2 ?? →
且 抛 物 线 C上 存 在 点 M,使 得 OA+OB= OM O p
3 ( 为 坐 标 原 点 ),则 的 值 为
1
A.4 B.2 C.1 D. 2
12.对 于 函 数 y=f(x),若 存 在 区 间 [a,b],当 x∈ [a,b]时 ,f(x)的 值 域 为 [ka,kb],则 称
x
y=f(x)为 k倍 值 函 数 .若 f(x)=e 是 k倍 值 函 数 ,则 k的 取 值 范 围 为
1 1
A.(0, B. 1 e C. e +∞ D. +∞
e ) (,) (, ) (e , )
高 二 数 学 (文 科 )试 卷 第 2页 (共 4 页 )
二 、填 空 题 (本 大 题 共 4 小 题 ,共 20 分 .)
π π
13.若 “? x∈ [- 4 ,4 ],m≤ tanx+1”为 真 命 题 ,则 实 数 m的 最 大 值 为 .
14.有 人 发 现 ,多 看 手 机 容 易 使 人 近 视 ,下 表 是 调 查 机 构 对 此 现 象 的 调 查 数 据 :
近 视 不 近 视 总 计
少 看 手 机 15 45 60
多 看 手 机 15 5 20
总 计 30 50 80
则 在 犯 错 误 的 概 率 不 超 过 的 前 提 下 认 为 近 视 与 多 看 手 机 有 关 系 .
附 表 :
2
P(K ≥ k) 0.15 0.10 0.05 0.010 0.025 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
2
2 n(ad-bc)
参 考 公 式 :K = n=a+b+c+d.
(a+b ,其 中
)(c+d)(a+c)(b+d)
2 2
x y
15.设 椭 圆 2 + 2 =1 a>b>0 F1 F2 A AF2⊥ F1F2
a b ( )的 左 、右 焦 点 分 别 为 , , 是 椭 圆 上 一 点 , ,
1
若 原 点 O到 直 线 AF1 的 距 离 为 |OF1| .
3 ,则 该 椭 圆 的 离 心 率 为
lnx2 -lnx1
16.若 对 任 意 的 x1,x2∈ (m,+ ∞),且 x1 < x2,都 有 < e m
x2 -x ,则 的 最 小 值 是
1
.
三 、解 答 题 :(本 大 题 共 6 个 小 题 ,共 70 分 .解 答 应 写 出 必 要 的 文 科 字 说 明 ,证 明 过 程 或 演
算 步 骤 .)
17.(本 小 题 满 分 10 分 )
2
(1)求 曲 线 y=x +x-2 在 点 (1,0)的 切 线 方 程 .
(2)求 经 过 点 A(3,1),焦 点 在 坐 标 轴 上 的 等 轴 双 曲 线 的 标 准 方 程 .
18.(本 小 题 满 分 12 分 )
2
已 知 抛 物 线 C:y =4x,坐 标 原 点 为 O,焦 点 为 F,直 线 l:y=kx+1.
(1)若 l与 C相 切 ,求 k的 值 ;
(2)过 点 F作 斜 率 为 1 的 直 线 交 抛 物 线 C于 A、B两 点 ,求 △ OAB的 面 积 .
19.(本 小 题 满 分 12 分 )
3
已 知 函 数 f(x)=ax +bx在 x=1 处 有 极 值 2.
(1)求 a,b的 值 ; 1
(2)求 函 数 f(x)在 区 间 [-2,2 ]上 的 最 值 .
高 二 数 学 (文 科 )试 卷 第 3页 (共 4 页 )
20.(本 小 题 满 分 12 分 )
为 了 选 拔 培 养 有 志 于 服 务 国 家 重 大 战 略 需 求 且 综 合 素 质 优 秀 或 基 础 学 科 拔 尖 的 学 生 ,教
育 部 开 展 了 招 生 改 革 工 作 ———强 基 计 划 .现 对 某 高 中 学 校 学 生 对 强 基 课 程 学 习 的 情 况 进 行 调
查 ,在 参 加 数 学 和 物 理 的 强 基 计 划 课 程 学 习 的 学 生 中 ,随 机 抽 取 了 10 名 学 生 .
(1)在 某 次 数 学 强 基 课 程 的 测 试 中 ,这 10 名 学 生 成 绩 的 统 计 数 据 如 茎 叶 图 所 示 ,其 中 某
男 生 的 成 绩 被 污 损 ,求 女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 的 概 率 .
男 生 女 生
3 6 7 8 9 8
? 9 9 3 2 1
(2)已 知 学 生 的 物 理 成 绩 y与 数 学 成 绩 x是 线 性 相 关 的 ,现 统 计 了 小 明 同 学 连 续 5 次 在 强
基 课 程 测 试 中 的 数 学 和 物 理 成 绩 (如 下 表 ).若 第 6 次 测 试 该 生 的 数 学 成 绩 达 到 132,请 你 估 计
第 6 次 测 试 他 的 物 理 成 绩 大 约 是 多 少 ?
数 学 成 绩 x 120 118 116 122 124
物 理 成 绩 y 79 79 77 82 83
n
∧ i∑ x -x珋 y -y珋
=1(i )(i ) ∧ ∧
附 :b = n a =y珋 -bx珋 .
2 ,
i∑ x -x珋
=1(i )
21.(本 小 题 满 分 12 分 )
2
x 2
已 知 直 线 l:y=x+m与 椭 圆 C: +y =1 A B .
3 交 于 、 两 点
(1)若 直 线 l过 椭 圆 C的 左 焦 点 F1,求 弦 长 |AB|的 值 ;
1
(2)若 线 段 AB的 垂 直 平 分 线 与 x轴 交 于 点 N( 0 m .
2 ,),求 的 值
22.(本 小 题 满 分 12 分 )
1 3
已 知 函 数 f(x)= x +tx+t.
3
(1)当 t= -1 时 ,求 函 数 f(x)的 单 调 区 间 ;
(2)讨 论 函 数 f(x)的 零 点 个 数 ,并 比 较 零 点 与 0 的 大 小 .
高 二 数 学 (文 科 )试 卷 第 4页 (共 4 页 )
内 江 市 高 中 2022 届 零 模 试 题
数 学 (文 科 )参 考 答 案 及 评 分 意 见
一 、选 择 题 :本 大 题 共 12 个 小 题 ,每 小 题 5 分 ,共 60 分 .
1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.A 9.D 10.B 11.B 12.C
二 、填 空 题 :本 大 题 共 4 个 小 题 ,每 小 题 5 分 ,共 20 分 .
2 1
13.0 14.0.001 15.槡 16.
2 e
三 、解 答 题 :本 大 题 共 6 个 小 题 ,共 70 分 .
2
17.解 :(1)对 y=x +x-2 求 导 ,得 y′=2x+1
!!!!!!!!!!!!!!!!!! 1 分
则 切 线 的 斜 率 k=2 ×1 +1 =3
!!!!!!!!!!!!!!!!!!!!!! 3 分
∴ 切 线 方 程 为 y=3x-3.
!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
2 2
(2)设 双 曲 线 的 方 程 为 x -y =λ,
!!!!!!!!!!!!!!!!!!!!! 7 分
2 2
把 点 A(3,1)代 入 x -y =λ,得 λ=9 -1 =8.
!!!!!!!!!!!!!!!! 9 分
2 2
x y
故 所 求 方 程 为 - =1.
!!!!!!!!!!!!!!!!!!!!!!!! 10
8 8 分
y=kx+1 2 2
18.解 :(1)联 立 2 ,消 去 y,得 k x +(2k-4)x+1 =0.
!!!!!!!!!!! 2 分
{y =4x
由 直 线 l与 抛 物 线 C相 切 ,则 k≠ 0
!!!!!!!!!!!!!!!!!!!! 3 分
2 2
△ =(2k-4)-4k =16(1 -k)=0,即 k=1.
!!!!!!!!!!!!!!!! 6 分
(2)焦 点 F(1,0),直 线 l的 方 程 为 y=x-1,
!!!!!!!!!!!!!!!!! 7 分
设 A(x1,y1),B(x2,y2).
2
联 立 直 线 与 抛 物 线 的 方 程 整 理 得 x -6x+1 =0,∴ x1 +x2 =6.
|AB| =x1 +x2 +2 =8
!!!!!!!!!!!!!!!!!!!!!!!!!! 8 分
1 2
点 O到 直 线 l的 距 离 d= =槡 .
!!!!!!!!!!!!!!!!!!! 10 分
1 +1 2
槡
1 2
所 以 S△ OAB = ×8 ×槡 =2 2.
!!!!!!!!!!!!!!!!!!!!!! 12
2 2 槡 分
3 2
19.解 :(1)f(x)=ax +bx,f′(x)=3ax +b
!!!!!!!!!!!!!!!!!!! 1 分
3
∵ 函 数 f(x)=ax +bx在 x=1 处 取 得 极 值 2,
∴ f(1)=a+b=2,f′(1)=3a+b=0
!!!!!!!!!!!!!!!!!!!! 3 分
解 得 a= -1,b=3
!!!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
3
f(x)= -x +3x,经 验 证 在 x=1 处 取 极 值 2,
故 a= -1,b=3
!!!!!!!!!!!!!!!!!!!!!!!!!!!! 6 分 ,
(2)由 f′(x)= -3(x+1)(x-1),令 f′(x)>0,解 得 -1 <x<1
令 f′(x)<0,解 得 x>1 或 x< -1,
!!!!!!!!!!!!!!!!!!!!! 8 分
1
因 此 ,f(x)在 [-2,-1)递 减 ,在 (-1,2 ]递 增 ,
f(x)的 最 小 值 是 f(-1)= -2
!!!!!!!!!!!!!!!!!!!!!! 10 分
高 二 数 学 (文 科 )试 题 答 案 第 1页 (共 3 页 )
1 11
而 f(-2)=2 >f( =
!!!!!!!!!!!!!!!!!!!!!!! 11
2 ) 8 , 分
故 函 数 f(x)的 最 大 值 是 2.
!!!!!!!!!!!!!!!!!!!!!!! 12 分
20.解 :(1)设 被 污 损 的 数 字 为 a,则 共 有 10 种 情 况 .
!!!!!!!!!!!!!!! 2 分
由 88 +89 +91 +92 +93 >83 +86 +87 +90 +a+99,得 a<8,
故 有 8 种 情 况 使 得 女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 .
!!!!!!!!!!! 4 分
令 事 件 A:女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 .
8 4
则 P(A)= = .
!!!!!!!!!!!!!!!!!!!!!!!!!!! 6
10 5 分
1
(2)由 x珋 = × 120 +118 +116 +122 +124 =120
5 ( )
y珋 1
= × 79 +79 +77 +82 +83 =80
5 ( )
n
∧ i∑ x -x珋 y -y珋
=1(i )(i ) 0 × -1 + -2 × -1 + -4 × -3 +2 ×2 +4 ×3
得 b = ( ) ( ) ( ) ( ) ( )
n =
2 2 2 2 2 2
i∑ x -x珋 0 +(-2)+(-4)+2 +4
=1(i )
3
=
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 9
4 分
∧ ∧
a =y珋 -bx珋 3
=80 - ×120 = -10
4
3
所 以 y关 于 x的 线 性 回 归 方 程 是 y= x-10
!!!!!!!!!!!!!!! 11
4 分
3 3
当 x=132 时 ,y= x-10 = ×132 -10 =89
4 4 ,
故 估 计 第 6 次 测 试 他 的 物 理 成 绩 为 89 分 .
!!!!!!!!!!!!!!!!! 12 分
2 2 2
21.解 :(1)由 题 知 ,c =a -b =2,左 焦 点 F1(- 2 0 1
槡 ,)
!!!!!!!!!!!!!! 分
则 直 线 l的 方 程 为 y=x+ 2 A x y
槡 ,设 (1,1)、B(x2,y2),
y=x+ 2 2
联 立 方 程 槡
2 2 ,得 4x +6 2x+3 =0,
!!!!!!!!!!!!!!!! 3 分
{x +3y =3 槡
3 2 3
所 以 △ =72 -48 >0,x1 +x2 = - 槡
2 ,x1x2 = 4 ,
2 3 2 2
所 以 |AB| = 2 x +x -4x x = 2 - 槡 -3 = 3. 5
槡 [(1 2) 1 2] [( ) ]
!!!!!!!! 分
槡 2 槡
2 槡
()设 A(x1,y1)、B(x2,y2),AB的 中 点 M(x0,y0),
y=x+m 2 2 2
联 立 方 程 2 2 ,得 4x +6mx+3m -3 =0,△ =48 -12m >0,
{x +3y =3
3m
∴ x1 +x2 = -
!!!!!!!!!!!!!!!!!!!!!!!!!!!! 6
2 分
3 3 m
x0 = - m y0 = - m+m=
4 , 4 4 ,
3 m
故 点 M的 坐 标 为 (- m
!!!!!!!!!!!!!!!!!!!!!!! 8
4 ,4 ) 分
高 二 数 学 (文 科 )试 题 答 案 第 2页 (共 3 页 )
1
∵ 线 段 AB的 垂 直 平 分 线 与 x轴 交 于 点 N( 0
2 ,)
1
∴ 线 段 AB的 垂 直 平 分 线 方 程 为 y= -x+ .
!!!!!!!!!!!!!!! 10
2 分
1 m 3 1
由 AB中 点 M在 直 线 y= -x+ = m+ .
2 上 ,知 4 4 2
解 得 m= -1(满 足 △ >0),因 此 m的 值 为 -1.
!!!!!!!!!!!!!!! 12 分
1 3 2
22.解 :(1)当 t= -1 时 ,f(x)= x -x-1 f′ x =x -1
!!!!!!!!!!!!! 1
3 ,() 分
f′(x)>0 的 解 集 为 (-∞,-1)∪ (1,+∞),f′(x)<0 的 解 集 为 (-1,1)
则 f(x)在 (-1,1)上 单 调 递 减 ,在 (-∞,-1),(1,+∞)上 单 调 递 增
!!!!!! 3 分
1 3 2
(2)f(x)= x +tx+t f′ x =x +t
3 ,()
1 3
①当 t=0 时 ,f(x)= x f x x0 =0
!!!!!!!!!!!!!! 4
3 ,()有 唯 一 零 点 分
②当 t>0 时 ,f′(x)>0,则 f(x)在 R上 单 调 递 增 ,f(x)有 唯 一 零 点 x0
由 f(0)=t>0 知 x0 <0
!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
③当 t<0 时 ,令 f′(x)=0,得 x= ± -t
槡 ,
则 f(x)在 (- -t -t
槡 ,槡 )上 单 调 递 减 ,在 (-∞,- -t -t +
槡 ),(槡 , ∞)上 单 调 递 增
2
因 此 ,f(x)的 极 小 值 为 f( -t =t+ t -t<0
槡 ) 3 槡 ,
2
极 大 值 为 f(- -t =t- t -t. 7
槡 )
!!!!!!!!!!!!!!!!!!!!
3 槡 分
9
1)当 f(- -t =0 t= - f x x x x <0 <x 9
槡 ) ,即 1 2 1 2
4 时 ,函 数 ()有 两 个 零 点 、 ,且
!! 分
9
2)当 f(- -t <0 0 >t> -
槡 ) ,即 4 时 ,
函 数 f(x)仅 有 一 个 零 点 x1,且 x1 >0
!!!!!!!!!!!!!!!!!!! 10 分
9
3)当 f(- -t >0
槡 ) ,即 t< - 4 时 ,
函 数 f(x)有 三 个 不 同 的 零 点 x1、x2、x3
2 2
又 f( -t =t+ t -t<0 f - -t =t- t -t>0 f 0 =t<0
槡 ) 3 槡 ,( 槡 ) 3 槡 ,()
且 当 x→ +∞时 ,有 f(x)→ +∞,当 x→ -∞时 ,有 f(x)→ -∞
所 以 由 零 点 存 在 性 定 理 知 x1 < - -t<x <0 < -t<x . 12
槡 2 槡 3
!!!!!!!!! 分
高 二 数 学 (文 科 )试 题 答 案 第 3页 (共 3 页 )
数 学 (文 科 )
本 试 卷 共 4 页 ,全 卷 满 分 150 分 ,考 试 时 间 120 分 钟 。
注 意 事 项 :
1.答 题 前 ,考 生 务 必 将 自 己 的 姓 名 、考 号 、班 级 用 签 字 笔 填 写 在 答 题 卡 相 应 位 置 .
2.选 择 题 选 出 答 案 后 ,用 铅 笔 把 答 题 卡 上 对 应 题 目 的 答 案 标 号 涂 黑 。如 需 改 动 ,用 橡 皮 擦
干 净 后 ,再 选 涂 其 它 答 案 。不 能 答 在 试 题 卷 上 。
3.非 选 择 题 用 签 字 笔 将 答 案 直 接 答 在 答 题 卡 相 应 位 置 上 。
4.考 试 结 束 后 ,监 考 人 员 将 答 题 卡 收 回 。
一 、选 择 题 :(本 大 题 共 12 个 小 题 ,每 小 题 5 分 ,共 60 分 .在 每 小 题 的 四 个 选 项 中 只 有 一 个
是 正 确 的 ,把 正 确 选 项 的 代 号 填 涂 在 答 题 卡 的 指 定 位 置 上 .)
1.复 数 z满 足 z(1 -i)=i(i为 虚 数 单 位 ),则 z的 虚 部 为
1 1 1 1
A. - B. C. i D. - i
2 2 2 2
π
2.设 f(x)=xcosx,则 f′( =
2 )
π π
A. B. - C.1 D. -1
2 2
2 2
3.若 双 曲 线 mx -y =1(m>0)的 离 心 率 为 2,则 m=
1 1
A. B. 3 C. 3 D.3
3 槡 3 或
x
4.设 命 题 p:函 数 f(x)=2 在 R上 为 单 调 递 增 函 数 ;命 题 q:函 数 f(x)=cos2x 为 奇 函 数 ,
则 下 列 命 题 中 真 命 题 是
A.p∧ q B.(? p)∧ (? q) C.(? p)∨ q D.p∧ (? q)
5.曲 线 y=f(x)在 x=1 处 的 切 线 如 图 所 示 ,则 f′(1)-f(1)=
A.0 B.2
C. -2 D. -1
2 2
x y
6.以 椭 圆 C:2 + 2 =1 a>b>0
a b ( )的 短 轴 的 一 个 端 点 和 两 焦 点 为
顶 点 的 三 角 形 为 等 边 三 角 形 ,且 椭 圆 C上 的 点 到 左 焦 点 的 最 大 距 离 为 6,则 椭 圆 C的 标 准 方 程
为
2 2 2 2
x y x y
A. + =1 B. + =1
4 3 8 4
2 2 2 2
x y x y
C. + =1 D. + =1
16 12 64 48
7.对 于 下 表 格 中 的 数 据 进 行 回 归 分 析 时 ,下 列 四 个 函 数 模 型 拟 合 效 果 最 优 的 是
x 1 2 3
y 3 5.99 12.01
x-1 2
A.y=3 ×2 B.y=log2x C.y=3x D.y=x
高 二 数 学 (文 科 )试 卷 第 1页 (共 4 页 )
x
8.已 知 函 数 f(x)=e -ax,则 “a<0”是 “函 数 f(x)为 增 函 数 ”的
A.充 分 不 必 要 条 件 B.必 要 不 充 分 条 件
C.充 要 条 件 D.既 不 充 分 也 不 必 要 条 件
9.“二 进 制 ”来 源 于 我 国 古 代 的 《易 经 》,二 进 制 数 由 数 字 0 和 1 组 成 ,比 如 :二 进 制 数
2 1 0
011(2)化 为 十 进 制 的 计 算 公 式 如 下 :011(2)=0 ×2 +1 ×2 +1 ×2 =3(10).若 从 二 进 制 数 11(2)、
00(2)、10(2)、01(2)中 任 选 一 个 数 字 ,则 二 进 制 数 所 对 应 的 十 进 制 数 大 于 2 的 概 率 为
1 1 2 1
A. B. C. D.
2 3 3 4
10.空 气 质 量 指 数 AQI是 反 映 空 气 质 量 状 况 的 指 数 ,其 对 应 关 系 如 下 表 :
AQI指 数 值 0 ~50 51 ~100 101 ~150 151 ~200 201 ~300 >300
空 气 质 量 优 良 轻 度 污 染 中 度 污 染 重 度 污 染 严 重 污 染
为 监 测 某 化 工 厂 排 放 废 气 对 周 边 空 气 质 量 指 数 的 影 响 ,某 科 学 兴 趣 小 组 测 得 10 月 1 日 -
20 日 AQI指 数 的 数 据 并 绘 成 折 线 图 如 下 :
下 列 叙 述 正 确 的 是
A.这 20 天 中 AQI指 数 值 的 中 位 数 略 大 于 150
1
B.这 20 天 中 的 空 气 质 量 为 优 的 天 数 占 4
C.10 月 4 日 到 10 月 11 日 ,空 气 质 量 越 来 越 好
D.总 体 来 说 ,10 月 中 旬 的 空 气 质 量 比 上 旬 的 空 气 质 量 好
2
11.已 知 直 线 l:y=x-1 与 抛 物 线 C:y =2px(p>0)相 交 于 A、B 两 点 ,若 AB 的 中 点 为 N,
??→ ?? → 2 ?? →
且 抛 物 线 C上 存 在 点 M,使 得 OA+OB= OM O p
3 ( 为 坐 标 原 点 ),则 的 值 为
1
A.4 B.2 C.1 D. 2
12.对 于 函 数 y=f(x),若 存 在 区 间 [a,b],当 x∈ [a,b]时 ,f(x)的 值 域 为 [ka,kb],则 称
x
y=f(x)为 k倍 值 函 数 .若 f(x)=e 是 k倍 值 函 数 ,则 k的 取 值 范 围 为
1 1
A.(0, B. 1 e C. e +∞ D. +∞
e ) (,) (, ) (e , )
高 二 数 学 (文 科 )试 卷 第 2页 (共 4 页 )
二 、填 空 题 (本 大 题 共 4 小 题 ,共 20 分 .)
π π
13.若 “? x∈ [- 4 ,4 ],m≤ tanx+1”为 真 命 题 ,则 实 数 m的 最 大 值 为 .
14.有 人 发 现 ,多 看 手 机 容 易 使 人 近 视 ,下 表 是 调 查 机 构 对 此 现 象 的 调 查 数 据 :
近 视 不 近 视 总 计
少 看 手 机 15 45 60
多 看 手 机 15 5 20
总 计 30 50 80
则 在 犯 错 误 的 概 率 不 超 过 的 前 提 下 认 为 近 视 与 多 看 手 机 有 关 系 .
附 表 :
2
P(K ≥ k) 0.15 0.10 0.05 0.010 0.025 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
2
2 n(ad-bc)
参 考 公 式 :K = n=a+b+c+d.
(a+b ,其 中
)(c+d)(a+c)(b+d)
2 2
x y
15.设 椭 圆 2 + 2 =1 a>b>0 F1 F2 A AF2⊥ F1F2
a b ( )的 左 、右 焦 点 分 别 为 , , 是 椭 圆 上 一 点 , ,
1
若 原 点 O到 直 线 AF1 的 距 离 为 |OF1| .
3 ,则 该 椭 圆 的 离 心 率 为
lnx2 -lnx1
16.若 对 任 意 的 x1,x2∈ (m,+ ∞),且 x1 < x2,都 有 < e m
x2 -x ,则 的 最 小 值 是
1
.
三 、解 答 题 :(本 大 题 共 6 个 小 题 ,共 70 分 .解 答 应 写 出 必 要 的 文 科 字 说 明 ,证 明 过 程 或 演
算 步 骤 .)
17.(本 小 题 满 分 10 分 )
2
(1)求 曲 线 y=x +x-2 在 点 (1,0)的 切 线 方 程 .
(2)求 经 过 点 A(3,1),焦 点 在 坐 标 轴 上 的 等 轴 双 曲 线 的 标 准 方 程 .
18.(本 小 题 满 分 12 分 )
2
已 知 抛 物 线 C:y =4x,坐 标 原 点 为 O,焦 点 为 F,直 线 l:y=kx+1.
(1)若 l与 C相 切 ,求 k的 值 ;
(2)过 点 F作 斜 率 为 1 的 直 线 交 抛 物 线 C于 A、B两 点 ,求 △ OAB的 面 积 .
19.(本 小 题 满 分 12 分 )
3
已 知 函 数 f(x)=ax +bx在 x=1 处 有 极 值 2.
(1)求 a,b的 值 ; 1
(2)求 函 数 f(x)在 区 间 [-2,2 ]上 的 最 值 .
高 二 数 学 (文 科 )试 卷 第 3页 (共 4 页 )
20.(本 小 题 满 分 12 分 )
为 了 选 拔 培 养 有 志 于 服 务 国 家 重 大 战 略 需 求 且 综 合 素 质 优 秀 或 基 础 学 科 拔 尖 的 学 生 ,教
育 部 开 展 了 招 生 改 革 工 作 ———强 基 计 划 .现 对 某 高 中 学 校 学 生 对 强 基 课 程 学 习 的 情 况 进 行 调
查 ,在 参 加 数 学 和 物 理 的 强 基 计 划 课 程 学 习 的 学 生 中 ,随 机 抽 取 了 10 名 学 生 .
(1)在 某 次 数 学 强 基 课 程 的 测 试 中 ,这 10 名 学 生 成 绩 的 统 计 数 据 如 茎 叶 图 所 示 ,其 中 某
男 生 的 成 绩 被 污 损 ,求 女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 的 概 率 .
男 生 女 生
3 6 7 8 9 8
? 9 9 3 2 1
(2)已 知 学 生 的 物 理 成 绩 y与 数 学 成 绩 x是 线 性 相 关 的 ,现 统 计 了 小 明 同 学 连 续 5 次 在 强
基 课 程 测 试 中 的 数 学 和 物 理 成 绩 (如 下 表 ).若 第 6 次 测 试 该 生 的 数 学 成 绩 达 到 132,请 你 估 计
第 6 次 测 试 他 的 物 理 成 绩 大 约 是 多 少 ?
数 学 成 绩 x 120 118 116 122 124
物 理 成 绩 y 79 79 77 82 83
n
∧ i∑ x -x珋 y -y珋
=1(i )(i ) ∧ ∧
附 :b = n a =y珋 -bx珋 .
2 ,
i∑ x -x珋
=1(i )
21.(本 小 题 满 分 12 分 )
2
x 2
已 知 直 线 l:y=x+m与 椭 圆 C: +y =1 A B .
3 交 于 、 两 点
(1)若 直 线 l过 椭 圆 C的 左 焦 点 F1,求 弦 长 |AB|的 值 ;
1
(2)若 线 段 AB的 垂 直 平 分 线 与 x轴 交 于 点 N( 0 m .
2 ,),求 的 值
22.(本 小 题 满 分 12 分 )
1 3
已 知 函 数 f(x)= x +tx+t.
3
(1)当 t= -1 时 ,求 函 数 f(x)的 单 调 区 间 ;
(2)讨 论 函 数 f(x)的 零 点 个 数 ,并 比 较 零 点 与 0 的 大 小 .
高 二 数 学 (文 科 )试 卷 第 4页 (共 4 页 )
内 江 市 高 中 2022 届 零 模 试 题
数 学 (文 科 )参 考 答 案 及 评 分 意 见
一 、选 择 题 :本 大 题 共 12 个 小 题 ,每 小 题 5 分 ,共 60 分 .
1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.A 9.D 10.B 11.B 12.C
二 、填 空 题 :本 大 题 共 4 个 小 题 ,每 小 题 5 分 ,共 20 分 .
2 1
13.0 14.0.001 15.槡 16.
2 e
三 、解 答 题 :本 大 题 共 6 个 小 题 ,共 70 分 .
2
17.解 :(1)对 y=x +x-2 求 导 ,得 y′=2x+1
!!!!!!!!!!!!!!!!!! 1 分
则 切 线 的 斜 率 k=2 ×1 +1 =3
!!!!!!!!!!!!!!!!!!!!!! 3 分
∴ 切 线 方 程 为 y=3x-3.
!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
2 2
(2)设 双 曲 线 的 方 程 为 x -y =λ,
!!!!!!!!!!!!!!!!!!!!! 7 分
2 2
把 点 A(3,1)代 入 x -y =λ,得 λ=9 -1 =8.
!!!!!!!!!!!!!!!! 9 分
2 2
x y
故 所 求 方 程 为 - =1.
!!!!!!!!!!!!!!!!!!!!!!!! 10
8 8 分
y=kx+1 2 2
18.解 :(1)联 立 2 ,消 去 y,得 k x +(2k-4)x+1 =0.
!!!!!!!!!!! 2 分
{y =4x
由 直 线 l与 抛 物 线 C相 切 ,则 k≠ 0
!!!!!!!!!!!!!!!!!!!! 3 分
2 2
△ =(2k-4)-4k =16(1 -k)=0,即 k=1.
!!!!!!!!!!!!!!!! 6 分
(2)焦 点 F(1,0),直 线 l的 方 程 为 y=x-1,
!!!!!!!!!!!!!!!!! 7 分
设 A(x1,y1),B(x2,y2).
2
联 立 直 线 与 抛 物 线 的 方 程 整 理 得 x -6x+1 =0,∴ x1 +x2 =6.
|AB| =x1 +x2 +2 =8
!!!!!!!!!!!!!!!!!!!!!!!!!! 8 分
1 2
点 O到 直 线 l的 距 离 d= =槡 .
!!!!!!!!!!!!!!!!!!! 10 分
1 +1 2
槡
1 2
所 以 S△ OAB = ×8 ×槡 =2 2.
!!!!!!!!!!!!!!!!!!!!!! 12
2 2 槡 分
3 2
19.解 :(1)f(x)=ax +bx,f′(x)=3ax +b
!!!!!!!!!!!!!!!!!!! 1 分
3
∵ 函 数 f(x)=ax +bx在 x=1 处 取 得 极 值 2,
∴ f(1)=a+b=2,f′(1)=3a+b=0
!!!!!!!!!!!!!!!!!!!! 3 分
解 得 a= -1,b=3
!!!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
3
f(x)= -x +3x,经 验 证 在 x=1 处 取 极 值 2,
故 a= -1,b=3
!!!!!!!!!!!!!!!!!!!!!!!!!!!! 6 分 ,
(2)由 f′(x)= -3(x+1)(x-1),令 f′(x)>0,解 得 -1 <x<1
令 f′(x)<0,解 得 x>1 或 x< -1,
!!!!!!!!!!!!!!!!!!!!! 8 分
1
因 此 ,f(x)在 [-2,-1)递 减 ,在 (-1,2 ]递 增 ,
f(x)的 最 小 值 是 f(-1)= -2
!!!!!!!!!!!!!!!!!!!!!! 10 分
高 二 数 学 (文 科 )试 题 答 案 第 1页 (共 3 页 )
1 11
而 f(-2)=2 >f( =
!!!!!!!!!!!!!!!!!!!!!!! 11
2 ) 8 , 分
故 函 数 f(x)的 最 大 值 是 2.
!!!!!!!!!!!!!!!!!!!!!!! 12 分
20.解 :(1)设 被 污 损 的 数 字 为 a,则 共 有 10 种 情 况 .
!!!!!!!!!!!!!!! 2 分
由 88 +89 +91 +92 +93 >83 +86 +87 +90 +a+99,得 a<8,
故 有 8 种 情 况 使 得 女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 .
!!!!!!!!!!! 4 分
令 事 件 A:女 生 的 平 均 分 数 超 过 男 生 的 平 均 分 数 .
8 4
则 P(A)= = .
!!!!!!!!!!!!!!!!!!!!!!!!!!! 6
10 5 分
1
(2)由 x珋 = × 120 +118 +116 +122 +124 =120
5 ( )
y珋 1
= × 79 +79 +77 +82 +83 =80
5 ( )
n
∧ i∑ x -x珋 y -y珋
=1(i )(i ) 0 × -1 + -2 × -1 + -4 × -3 +2 ×2 +4 ×3
得 b = ( ) ( ) ( ) ( ) ( )
n =
2 2 2 2 2 2
i∑ x -x珋 0 +(-2)+(-4)+2 +4
=1(i )
3
=
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 9
4 分
∧ ∧
a =y珋 -bx珋 3
=80 - ×120 = -10
4
3
所 以 y关 于 x的 线 性 回 归 方 程 是 y= x-10
!!!!!!!!!!!!!!! 11
4 分
3 3
当 x=132 时 ,y= x-10 = ×132 -10 =89
4 4 ,
故 估 计 第 6 次 测 试 他 的 物 理 成 绩 为 89 分 .
!!!!!!!!!!!!!!!!! 12 分
2 2 2
21.解 :(1)由 题 知 ,c =a -b =2,左 焦 点 F1(- 2 0 1
槡 ,)
!!!!!!!!!!!!!! 分
则 直 线 l的 方 程 为 y=x+ 2 A x y
槡 ,设 (1,1)、B(x2,y2),
y=x+ 2 2
联 立 方 程 槡
2 2 ,得 4x +6 2x+3 =0,
!!!!!!!!!!!!!!!! 3 分
{x +3y =3 槡
3 2 3
所 以 △ =72 -48 >0,x1 +x2 = - 槡
2 ,x1x2 = 4 ,
2 3 2 2
所 以 |AB| = 2 x +x -4x x = 2 - 槡 -3 = 3. 5
槡 [(1 2) 1 2] [( ) ]
!!!!!!!! 分
槡 2 槡
2 槡
()设 A(x1,y1)、B(x2,y2),AB的 中 点 M(x0,y0),
y=x+m 2 2 2
联 立 方 程 2 2 ,得 4x +6mx+3m -3 =0,△ =48 -12m >0,
{x +3y =3
3m
∴ x1 +x2 = -
!!!!!!!!!!!!!!!!!!!!!!!!!!!! 6
2 分
3 3 m
x0 = - m y0 = - m+m=
4 , 4 4 ,
3 m
故 点 M的 坐 标 为 (- m
!!!!!!!!!!!!!!!!!!!!!!! 8
4 ,4 ) 分
高 二 数 学 (文 科 )试 题 答 案 第 2页 (共 3 页 )
1
∵ 线 段 AB的 垂 直 平 分 线 与 x轴 交 于 点 N( 0
2 ,)
1
∴ 线 段 AB的 垂 直 平 分 线 方 程 为 y= -x+ .
!!!!!!!!!!!!!!! 10
2 分
1 m 3 1
由 AB中 点 M在 直 线 y= -x+ = m+ .
2 上 ,知 4 4 2
解 得 m= -1(满 足 △ >0),因 此 m的 值 为 -1.
!!!!!!!!!!!!!!! 12 分
1 3 2
22.解 :(1)当 t= -1 时 ,f(x)= x -x-1 f′ x =x -1
!!!!!!!!!!!!! 1
3 ,() 分
f′(x)>0 的 解 集 为 (-∞,-1)∪ (1,+∞),f′(x)<0 的 解 集 为 (-1,1)
则 f(x)在 (-1,1)上 单 调 递 减 ,在 (-∞,-1),(1,+∞)上 单 调 递 增
!!!!!! 3 分
1 3 2
(2)f(x)= x +tx+t f′ x =x +t
3 ,()
1 3
①当 t=0 时 ,f(x)= x f x x0 =0
!!!!!!!!!!!!!! 4
3 ,()有 唯 一 零 点 分
②当 t>0 时 ,f′(x)>0,则 f(x)在 R上 单 调 递 增 ,f(x)有 唯 一 零 点 x0
由 f(0)=t>0 知 x0 <0
!!!!!!!!!!!!!!!!!!!!!!!!! 5 分
③当 t<0 时 ,令 f′(x)=0,得 x= ± -t
槡 ,
则 f(x)在 (- -t -t
槡 ,槡 )上 单 调 递 减 ,在 (-∞,- -t -t +
槡 ),(槡 , ∞)上 单 调 递 增
2
因 此 ,f(x)的 极 小 值 为 f( -t =t+ t -t<0
槡 ) 3 槡 ,
2
极 大 值 为 f(- -t =t- t -t. 7
槡 )
!!!!!!!!!!!!!!!!!!!!
3 槡 分
9
1)当 f(- -t =0 t= - f x x x x <0 <x 9
槡 ) ,即 1 2 1 2
4 时 ,函 数 ()有 两 个 零 点 、 ,且
!! 分
9
2)当 f(- -t <0 0 >t> -
槡 ) ,即 4 时 ,
函 数 f(x)仅 有 一 个 零 点 x1,且 x1 >0
!!!!!!!!!!!!!!!!!!! 10 分
9
3)当 f(- -t >0
槡 ) ,即 t< - 4 时 ,
函 数 f(x)有 三 个 不 同 的 零 点 x1、x2、x3
2 2
又 f( -t =t+ t -t<0 f - -t =t- t -t>0 f 0 =t<0
槡 ) 3 槡 ,( 槡 ) 3 槡 ,()
且 当 x→ +∞时 ,有 f(x)→ +∞,当 x→ -∞时 ,有 f(x)→ -∞
所 以 由 零 点 存 在 性 定 理 知 x1 < - -t<x <0 < -t<x . 12
槡 2 槡 3
!!!!!!!!! 分
高 二 数 学 (文 科 )试 题 答 案 第 3页 (共 3 页 )
同课章节目录
