8.5.2直线与平面平行 教案——2020-2021学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.5.2直线与平面平行 教案——2020-2021学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 21:25:11 | ||
图片预览

文档简介
《课时备课工具——“导评用”案》
第
八
章:
第
5
单元
第
2
课时
共
3
课时
学
科
数学
课
型
新授课
课
题
8.5.2直线与平面平行(2)
知识梳理
特殊到一般,具体到抽象的思维方法
线线平行
本节知识
面面平行
转化划归的数学素养
教学重点
线面平行的判断和性质
教学难点
线面平行的性质
板书设计
线面平行的判断
例1
线面平行的性质
例2
综合运用
例3
学习目标
1.理解直线与平面平行,会用图形语言、文字语言、符号语言准确描述这个判定定理,并知道其地位和作用.
2.能够应用判定定理证明直线与平面平行.
3.理解直线与平面平行的性质定理的含义并能应用.
4.通过学习直线与平面平行的判定、性质,提升直观想象、逻辑推理的数学素养.
核心情境
观察我们的课桌面边沿所在的直线,该直线与地面有什么位置关系?
学习任务一:直线与平面平行的判定
学习评价:回忆直线与直线平行的定义,温故知新
教学过程:
直线与平面平行的判定定理
(1)文字语言:
一条直线与
的一条直线
,则该直线与此平面平行.?
(2)符号语言:
,
,
?l∥α.?
(3)图形语言:
特别提醒:利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
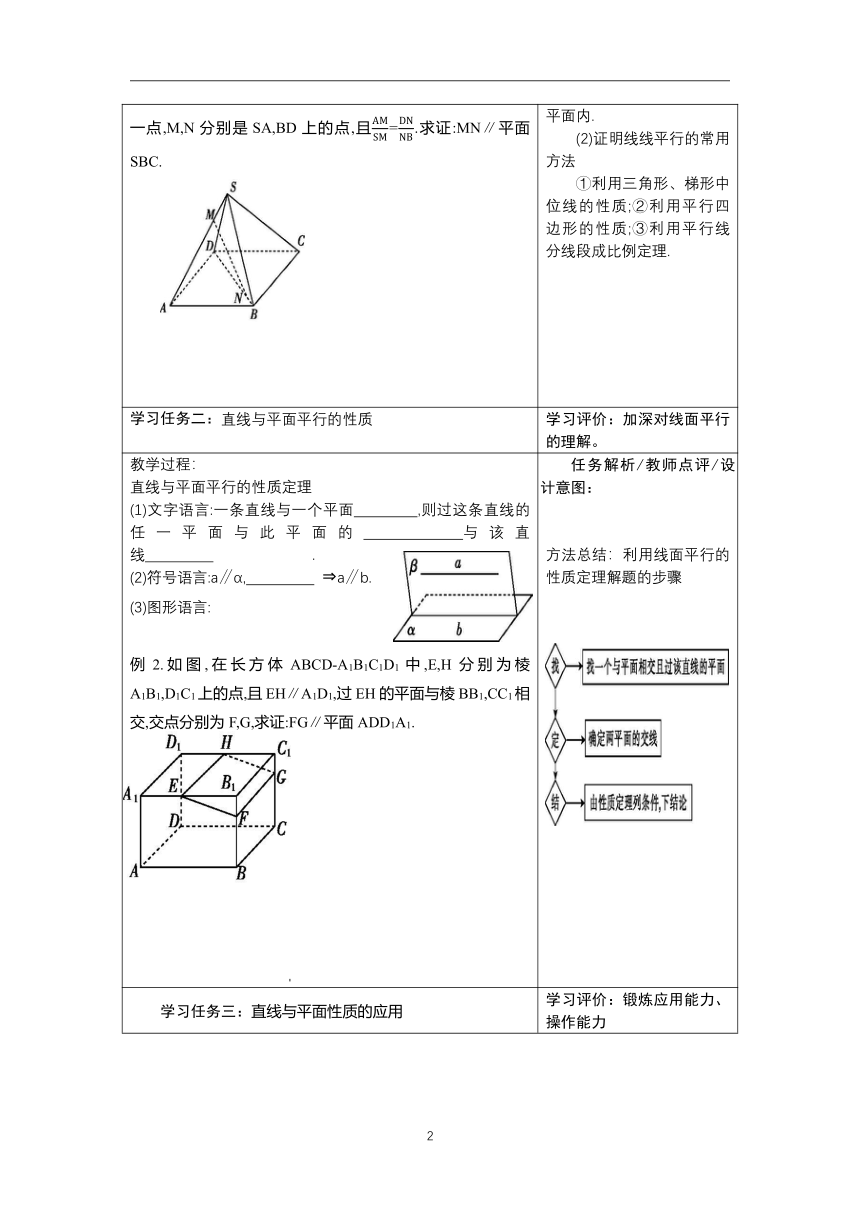
例1、如图,四边形ABCD是平行四边形,S是平面ABCD外
一点,M,N分别是SA,BD上的点,且=.求证:MN∥平面SBC.
任务解析/教师点评/设计意图:
方法总结:(1)判断或证明线面平行的常用方法
①定义法:证明直线与平面无公共点(不易操作).②判定定理法(a?α,b?α,a∥b?a∥α).③排除法:证明直线与平面不相交,直线也不在平面内.
(2)证明线线平行的常用方法
①利用三角形、梯形中位线的性质;②利用平行四边形的性质;③利用平行线分线段成比例定理.
学习任务二:直线与平面平行的性质
学习评价:加深对线面平行的理解。
教学过程:
直线与平面平行的性质定理
(1)文字语言:一条直线与一个平面
,则过这条直线的任一平面与此平面的
与该直线
.?
(2)符号语言:a∥α,
?a∥b.?
(3)图形语言:
例2.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
任务解析/教师点评/设计意图:
方法总结:利用线面平行的性质定理解题的步骤
学习任务三:直线与平面性质的应用
学习评价:锻炼应用能力、操作能力
教学过程:
例3.
如图,在三棱柱ABC-A1B1C1中,E,F分别是棱CC1,BB1上的点,M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M的位置.
任务解析/教师点评/设计意图:
利用线面平行的性质定理计算有关问题的三个关键点:
(1)根据已知线面平行关系推出线线平行关系;
(2)在三角形内利用三角形中位线的性质、平行线分线段成比例定理推出有关线段的关系;
(3)利用所得关系计算求值.
堂测:
如图,在三棱锥S-ABC中,E,F分别是SB,
SC上的点,
且EF∥平面ABC,则( ).
A.EF与BC相交
B.EF∥BC
C.EF与BC异面
D.以上均有可能
2.
过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在的平面的交线为l,则l与A1C1的位置关系是 .?
3.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度为 .?
4.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.证明:BC1∥平面A1CD.
课堂小结
课后作业
课堂反思
第
八
章:
第
5
单元
第
2
课时
共
3
课时
学
科
数学
课
型
新授课
课
题
8.5.2直线与平面平行(2)
知识梳理
特殊到一般,具体到抽象的思维方法
线线平行
本节知识
面面平行
转化划归的数学素养
教学重点
线面平行的判断和性质
教学难点
线面平行的性质
板书设计
线面平行的判断
例1
线面平行的性质
例2
综合运用
例3
学习目标
1.理解直线与平面平行,会用图形语言、文字语言、符号语言准确描述这个判定定理,并知道其地位和作用.
2.能够应用判定定理证明直线与平面平行.
3.理解直线与平面平行的性质定理的含义并能应用.
4.通过学习直线与平面平行的判定、性质,提升直观想象、逻辑推理的数学素养.
核心情境
观察我们的课桌面边沿所在的直线,该直线与地面有什么位置关系?
学习任务一:直线与平面平行的判定
学习评价:回忆直线与直线平行的定义,温故知新
教学过程:
直线与平面平行的判定定理
(1)文字语言:
一条直线与
的一条直线
,则该直线与此平面平行.?
(2)符号语言:
,
,
?l∥α.?
(3)图形语言:
特别提醒:利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
例1、如图,四边形ABCD是平行四边形,S是平面ABCD外
一点,M,N分别是SA,BD上的点,且=.求证:MN∥平面SBC.
任务解析/教师点评/设计意图:
方法总结:(1)判断或证明线面平行的常用方法
①定义法:证明直线与平面无公共点(不易操作).②判定定理法(a?α,b?α,a∥b?a∥α).③排除法:证明直线与平面不相交,直线也不在平面内.
(2)证明线线平行的常用方法
①利用三角形、梯形中位线的性质;②利用平行四边形的性质;③利用平行线分线段成比例定理.
学习任务二:直线与平面平行的性质
学习评价:加深对线面平行的理解。
教学过程:
直线与平面平行的性质定理
(1)文字语言:一条直线与一个平面
,则过这条直线的任一平面与此平面的
与该直线
.?
(2)符号语言:a∥α,
?a∥b.?
(3)图形语言:
例2.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
任务解析/教师点评/设计意图:
方法总结:利用线面平行的性质定理解题的步骤
学习任务三:直线与平面性质的应用
学习评价:锻炼应用能力、操作能力
教学过程:
例3.
如图,在三棱柱ABC-A1B1C1中,E,F分别是棱CC1,BB1上的点,M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M的位置.
任务解析/教师点评/设计意图:
利用线面平行的性质定理计算有关问题的三个关键点:
(1)根据已知线面平行关系推出线线平行关系;
(2)在三角形内利用三角形中位线的性质、平行线分线段成比例定理推出有关线段的关系;
(3)利用所得关系计算求值.
堂测:
如图,在三棱锥S-ABC中,E,F分别是SB,
SC上的点,
且EF∥平面ABC,则( ).
A.EF与BC相交
B.EF∥BC
C.EF与BC异面
D.以上均有可能
2.
过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在的平面的交线为l,则l与A1C1的位置关系是 .?
3.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度为 .?
4.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.证明:BC1∥平面A1CD.
课堂小结
课后作业
课堂反思
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
