4.3.3余角和补角 教案-人教版数学七年级上册
文档属性
| 名称 | 4.3.3余角和补角 教案-人教版数学七年级上册 |
|
|
| 格式 | zip | ||
| 文件大小 | 126.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 20:59:23 | ||
图片预览




文档简介
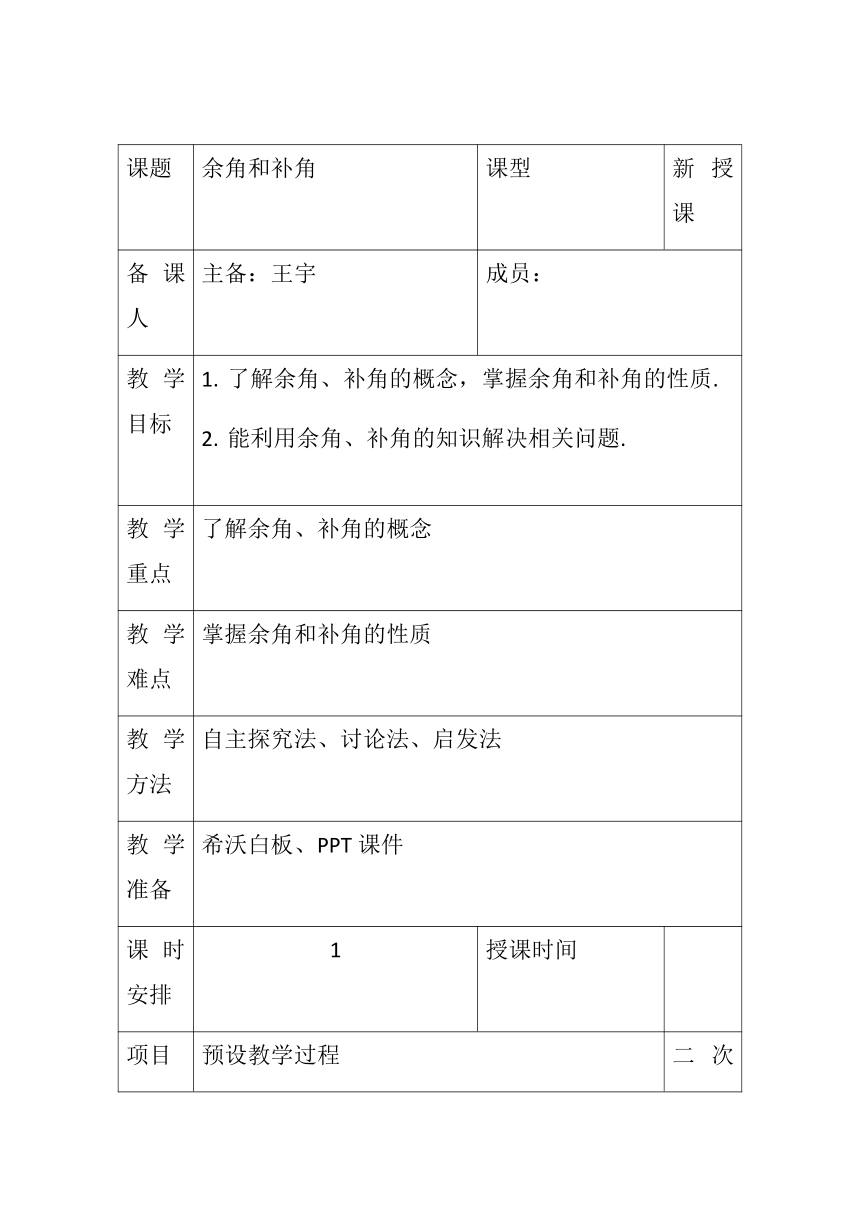
课题
余角和补角
课型
新授课
备课人
主备:王宇
成员:
教学目标
了解余角、补角的概念,掌握余角和补角的性质.
能利用余角、补角的知识解决相关问题.
教学重点
了解余角、补角的概念
教学难点
掌握余角和补角的性质
教学方法
自主探究法、讨论法、启发法
教学准备
希沃白板、PPT课件
课时安排
1
授课时间
项目
预设教学过程
二次备课
教
学
过
程
问题引入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
二、知识精讲
1.余角的概念
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
可以说
∠1
是
∠2
的余角,或
∠2
是∠1的余角,或
∠1和
∠2互余.
2.补角的概念
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互补.
填表并思考
观察可得结论:锐角的补角比它的余角大90°
4.余角和补角的性质
思考:∠1
与∠2,∠3都互为补角,∠2
与∠3
的大小有什么关系?
∠2=180°-∠1=∠3=180°-∠1
结论:同角
(等角)
的补角相等.
类似地,可以得到:同角
(等角)
的余角相等.
三、典例解析
1.若一个角的补角等于它的余角的
4
倍,求这个角的度数.
解:设这个角为
x°,则它的补角是
(
180-x
)°
余角是
(
90-x
)°
.
根据题意,得180-x
=
4
(
90-x
)
.解得x
=
60.
答:这个角的度数是
60
°.
2.已知
∠A
与∠B
互余,且
∠A
的度数比∠B
度数的
3
倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则
∠A
的度数为
(3x+30)°.
根据题意得:
x
+
(
3x+30
)
=
90.解得x=15.
故
∠B
的度数为15°.
达标检测
1.一个角的余角是它的2倍,这个角的度数是(A)
A.30°
B.45°
C.60°
D.75°
2.下列说法正确的是(D)
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是150°.
4.
∠1
与
∠2
互余,∠1
=
(6x
+
8)°,∠2
=
(4x-8)°,
则∠1=62°,∠2=28°.
5,.如图,已知∠AOB=90°,
∠AOC=
∠BOD,则与∠AOC互余的角有∠BOC
和
∠AOD.
小结归纳
项目
预设教学过程
板
书
设
计
4.3.2余角和补角
1.余角的概念:如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
2.补角的概念:如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
3.锐角的补角比它的余角大90°
4.余角和补角的性质
同角
(等角)
的补角相等.
同角
(等角)
的余角相等.
教
学
反
思
本节内容要求学生在对平面图形和立体图形知识的有一定了解的基础上,对简单图形——角的一个应用方面的概念和性质有个根本的了解,并进一步掌握数学中的几何语言的描述。新课程标准中指出,“动手实践,自主探索于合作交流是学生学习数学的重要方式”。课堂教学是学校教育的“主战场”,作为教师就要把指导学生养成自主、合作、探索的学习方式落实在课堂教学的实践中,而不仅仅是停留在理论层面上,教学中,教师可结合教材内容,并充分考虑初中学生的认知特点(如独立思考和探究的愿望和能力有所提高,并能在探究的过程中形成自己的观点,能在倾听他人意见的过程中逐渐完善自己的想法等等),把一些知识形成过程的典型材料设计为探究活动,充分拓宽学生探究与交流的空间,使学生经历观察、实验、猜测、推理、交流、反思等活动。
余角和补角
课型
新授课
备课人
主备:王宇
成员:
教学目标
了解余角、补角的概念,掌握余角和补角的性质.
能利用余角、补角的知识解决相关问题.
教学重点
了解余角、补角的概念
教学难点
掌握余角和补角的性质
教学方法
自主探究法、讨论法、启发法
教学准备
希沃白板、PPT课件
课时安排
1
授课时间
项目
预设教学过程
二次备课
教
学
过
程
问题引入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
二、知识精讲
1.余角的概念
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
可以说
∠1
是
∠2
的余角,或
∠2
是∠1的余角,或
∠1和
∠2互余.
2.补角的概念
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互补.
填表并思考
观察可得结论:锐角的补角比它的余角大90°
4.余角和补角的性质
思考:∠1
与∠2,∠3都互为补角,∠2
与∠3
的大小有什么关系?
∠2=180°-∠1=∠3=180°-∠1
结论:同角
(等角)
的补角相等.
类似地,可以得到:同角
(等角)
的余角相等.
三、典例解析
1.若一个角的补角等于它的余角的
4
倍,求这个角的度数.
解:设这个角为
x°,则它的补角是
(
180-x
)°
余角是
(
90-x
)°
.
根据题意,得180-x
=
4
(
90-x
)
.解得x
=
60.
答:这个角的度数是
60
°.
2.已知
∠A
与∠B
互余,且
∠A
的度数比∠B
度数的
3
倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则
∠A
的度数为
(3x+30)°.
根据题意得:
x
+
(
3x+30
)
=
90.解得x=15.
故
∠B
的度数为15°.
达标检测
1.一个角的余角是它的2倍,这个角的度数是(A)
A.30°
B.45°
C.60°
D.75°
2.下列说法正确的是(D)
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是150°.
4.
∠1
与
∠2
互余,∠1
=
(6x
+
8)°,∠2
=
(4x-8)°,
则∠1=62°,∠2=28°.
5,.如图,已知∠AOB=90°,
∠AOC=
∠BOD,则与∠AOC互余的角有∠BOC
和
∠AOD.
小结归纳
项目
预设教学过程
板
书
设
计
4.3.2余角和补角
1.余角的概念:如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
2.补角的概念:如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
3.锐角的补角比它的余角大90°
4.余角和补角的性质
同角
(等角)
的补角相等.
同角
(等角)
的余角相等.
教
学
反
思
本节内容要求学生在对平面图形和立体图形知识的有一定了解的基础上,对简单图形——角的一个应用方面的概念和性质有个根本的了解,并进一步掌握数学中的几何语言的描述。新课程标准中指出,“动手实践,自主探索于合作交流是学生学习数学的重要方式”。课堂教学是学校教育的“主战场”,作为教师就要把指导学生养成自主、合作、探索的学习方式落实在课堂教学的实践中,而不仅仅是停留在理论层面上,教学中,教师可结合教材内容,并充分考虑初中学生的认知特点(如独立思考和探究的愿望和能力有所提高,并能在探究的过程中形成自己的观点,能在倾听他人意见的过程中逐渐完善自己的想法等等),把一些知识形成过程的典型材料设计为探究活动,充分拓宽学生探究与交流的空间,使学生经历观察、实验、猜测、推理、交流、反思等活动。
