人教版 七年级数学上册 4.3.2 角的比较 教案
文档属性
| 名称 | 人教版 七年级数学上册 4.3.2 角的比较 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 06:29:37 | ||
图片预览

文档简介
《4.3.2角的比较与运算(1)》教学设计
教学目标:
1.运用类比的方法,学习比较两个角的大小,进一步认识角的大小关系,会分析图中角的和与角的差.
2.理解角的平分线、角的等分线的意义及数量关系.
重点:理解角比较方法,角的和与差,角的平分线的意义及数量关系,体会类比思想.
难点:用图形语言、文字语言、符号语言综合描述角的大小、角的和与差的关系
及角的平分线.
教法:自主探究,合作学习
教具:三角板、角的模型卡片、教学课件.
教学过程:
1、复习引入
线段的比较、线段的和差、线段的中点.
2、明确目标
三、新课探究
自主学习(一)
类比线段大小的比较,你认为该如何比较两个角的大小?用自己的角的卡片与同桌的相比较,交流比较角的大小的方法有几种?两个角的大小关系有几种?
自学检测(一)
教材136页练习第1题.
自主学习(二)
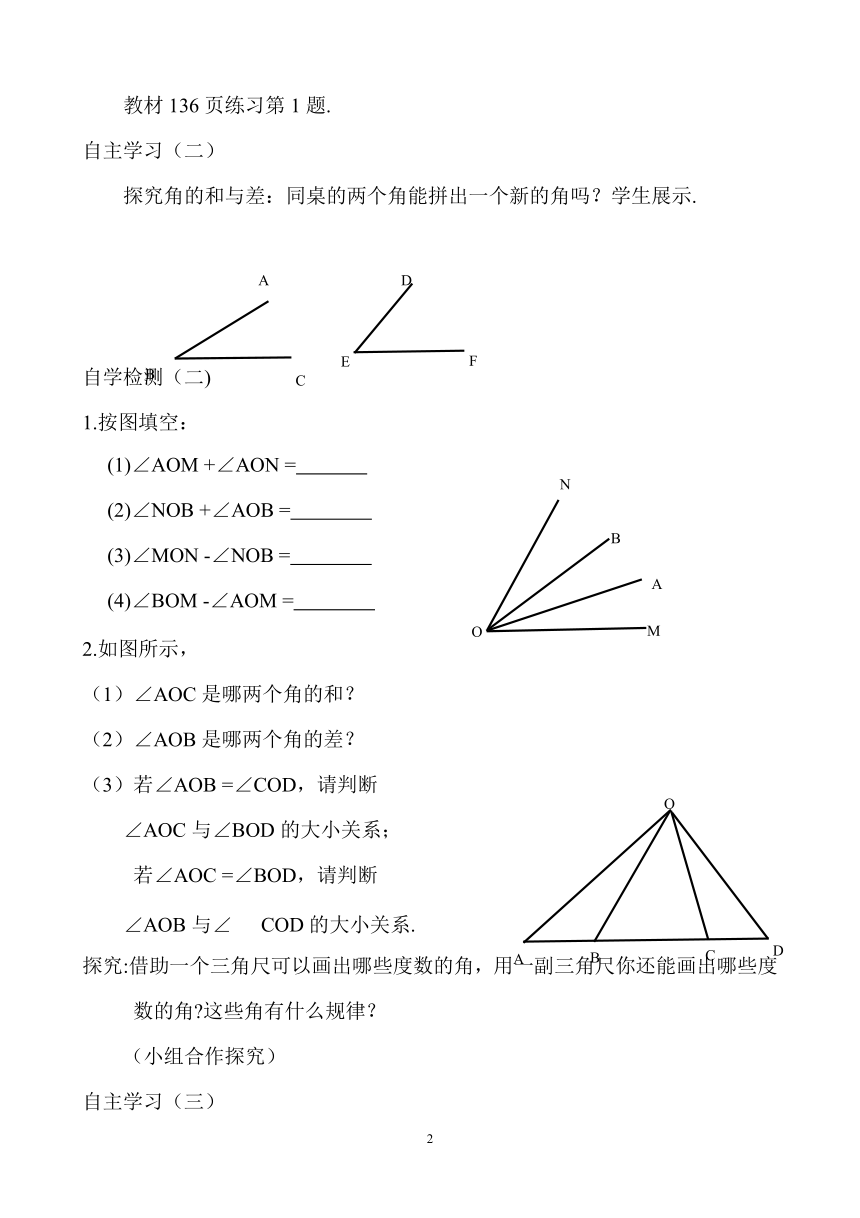
探究角的和与差:同桌的两个角能拼出一个新的角吗?学生展示.
自学检测(二)
1.按图填空:
2.如图所示,
(1)∠AOC是哪两个角的和?
(2)∠AOB是哪两个角的差?
(3)若∠AOB
=∠COD,请判断
∠AOC与∠BOD的大小关系;
若∠AOC
=∠BOD,请判断
∠AOB与∠COD的大小关系.
探究:借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角?这些角有什么规律?
(小组合作探究)
自主学习(三)
探究角的平分线的意义及数量关系:
类比线段的中点,射线OC有没有一种特殊的位置,若有,此时三个角之间又存在怎样的关系?
自学检测(三)
1.如图,OP是∠AOB的平分线,则下列说法错误的是(
)
(A)
∠AOB
=
2∠AOP
(B)
∠AOP
=
∠AOB
(C)
∠AOB
=
∠BOP
(D)
∠AOP
=∠BOP
2.如图,OB平分∠AOC,OC平分∠BOD,图中有哪些相等的角?还能得到哪些角的数量关系?
四、小结
学生质疑谈收获,教师解惑总结.
五、当堂检测
1.判断题
(打“√”或“×”)
(1)角的大小与它们的度数大小是一致的.
(
)
(2)若∠A+∠B>∠C,那么∠A一定大于∠C.
(
)
(3)用一副三角板可画出15°的角.
(
)
(4)平分一个角的射线叫做角的平分线.
(
)
2.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的
度数.
3.
如图,将长方形纸片的一角折叠,使顶点A落在A’处,EF为折痕,若EA’恰好平分∠FEB,
(1)判断∠FEA
与∠A’EB的大小关系;
(2)你能求出∠FEB的度数吗?
4.若∠AOB=2∠BOC,射线OC平分∠AOB吗?
这位同学做的对吗?
六、课后作业:
1.必做题:教材139页第4,5,6题
2.选做题:教材140页第9题
板书设计:
4.3.2角的比较与运算(1)
角的比较
角的和与差
角的平分线
E
F
D
A
B
C
E
F
D
A
B
C
A
B
M
N
O
∠AOM
+∠AON
=
(2)∠NOB
+∠AOB
=
(3)∠MON
-∠NOB
=
(1)(4)∠BOM
-∠AOM
=
O
A
B
C
D
O
B
P
A
C
D
B
A
O
E
D
F
A
C
B
A
PAGE
4
教学目标:
1.运用类比的方法,学习比较两个角的大小,进一步认识角的大小关系,会分析图中角的和与角的差.
2.理解角的平分线、角的等分线的意义及数量关系.
重点:理解角比较方法,角的和与差,角的平分线的意义及数量关系,体会类比思想.
难点:用图形语言、文字语言、符号语言综合描述角的大小、角的和与差的关系
及角的平分线.
教法:自主探究,合作学习
教具:三角板、角的模型卡片、教学课件.
教学过程:
1、复习引入
线段的比较、线段的和差、线段的中点.
2、明确目标
三、新课探究
自主学习(一)
类比线段大小的比较,你认为该如何比较两个角的大小?用自己的角的卡片与同桌的相比较,交流比较角的大小的方法有几种?两个角的大小关系有几种?
自学检测(一)
教材136页练习第1题.
自主学习(二)
探究角的和与差:同桌的两个角能拼出一个新的角吗?学生展示.
自学检测(二)
1.按图填空:
2.如图所示,
(1)∠AOC是哪两个角的和?
(2)∠AOB是哪两个角的差?
(3)若∠AOB
=∠COD,请判断
∠AOC与∠BOD的大小关系;
若∠AOC
=∠BOD,请判断
∠AOB与∠COD的大小关系.
探究:借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角?这些角有什么规律?
(小组合作探究)
自主学习(三)
探究角的平分线的意义及数量关系:
类比线段的中点,射线OC有没有一种特殊的位置,若有,此时三个角之间又存在怎样的关系?
自学检测(三)
1.如图,OP是∠AOB的平分线,则下列说法错误的是(
)
(A)
∠AOB
=
2∠AOP
(B)
∠AOP
=
∠AOB
(C)
∠AOB
=
∠BOP
(D)
∠AOP
=∠BOP
2.如图,OB平分∠AOC,OC平分∠BOD,图中有哪些相等的角?还能得到哪些角的数量关系?
四、小结
学生质疑谈收获,教师解惑总结.
五、当堂检测
1.判断题
(打“√”或“×”)
(1)角的大小与它们的度数大小是一致的.
(
)
(2)若∠A+∠B>∠C,那么∠A一定大于∠C.
(
)
(3)用一副三角板可画出15°的角.
(
)
(4)平分一个角的射线叫做角的平分线.
(
)
2.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的
度数.
3.
如图,将长方形纸片的一角折叠,使顶点A落在A’处,EF为折痕,若EA’恰好平分∠FEB,
(1)判断∠FEA
与∠A’EB的大小关系;
(2)你能求出∠FEB的度数吗?
4.若∠AOB=2∠BOC,射线OC平分∠AOB吗?
这位同学做的对吗?
六、课后作业:
1.必做题:教材139页第4,5,6题
2.选做题:教材140页第9题
板书设计:
4.3.2角的比较与运算(1)
角的比较
角的和与差
角的平分线
E
F
D
A
B
C
E
F
D
A
B
C
A
B
M
N
O
∠AOM
+∠AON
=
(2)∠NOB
+∠AOB
=
(3)∠MON
-∠NOB
=
(1)(4)∠BOM
-∠AOM
=
O
A
B
C
D
O
B
P
A
C
D
B
A
O
E
D
F
A
C
B
A
PAGE
4
