22.3.1 实际问题与二次函数课件(共26张PPT)
文档属性
| 名称 | 22.3.1 实际问题与二次函数课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
22.3实际问题与二次函数
---几何图形的最值问题
人教版
九年级上
教学目标
1.分析实际问题中变量之间的二次函数关系.(重点)
2.会运用二次函数解决几何图形有关的最大值或最小值.
3.函数特征与几何特征的相互转化以及最值在何处取得(难点)
回顾旧知
(1)二次函数y=a(x-h)2+k的对称轴是
,顶点坐标是
.
当x=
时,y的最值是
.
(2)
二次函数y=ax2+bx+c的对称轴是
,顶点坐标是
___
.当x=
____时,函数有最值,是
_____
.
x=h
(h,k)
k
h
填空
试一试:写出下列抛物线的开口方向、对称轴、顶点坐标及其最值.
(1)y=x2?4x?5;
(配方法)
(2)y=?x2?3x+4.(公式法)
(1)开口:向上;对称轴:x=2;
顶点:(2,?9);最小值:?9.
(2)开口:向下;对称轴:x=
;顶点:(
,
);最大值:
情境导入
随着毕业季的到来,毕业生们高兴的将学士帽一起高高抛向空中,我们知道将一个物体抛向空中,时间与高度将成二次函数关系,那么你知道学士帽最多可以抛多高吗?我们一起来研究一下此类问题。
合作探究
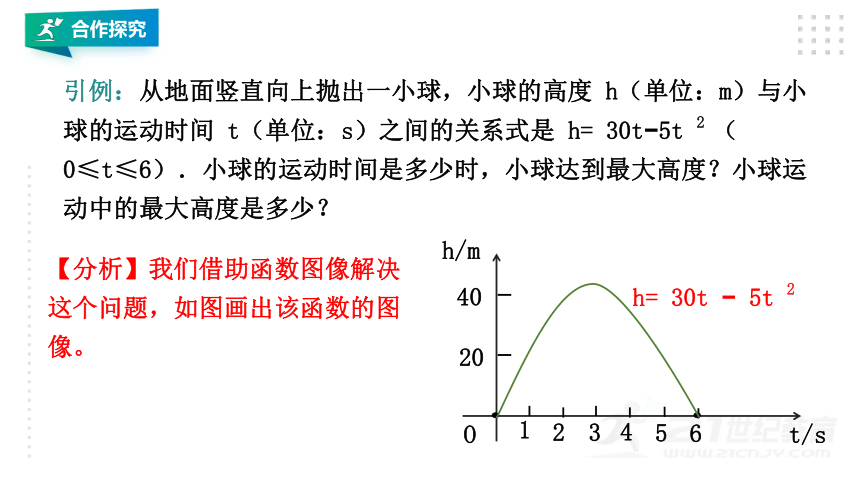
引例:从地面竖直向上抛出一小球,小球的高度
h(单位:m)与小球的运动时间
t(单位:s)之间的关系式是
h=
30t?5t
2
(0≤t≤6).小球的运动时间是多少时,小球达到最大高度?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h=
30t
?
5t
2
【分析】我们借助函数图像解决这个问题,如图画出该函数的图像。
合作探究
t/s
h/m
O
1
2
3
4
5
6
20
40
h=
30t
?
5t
2
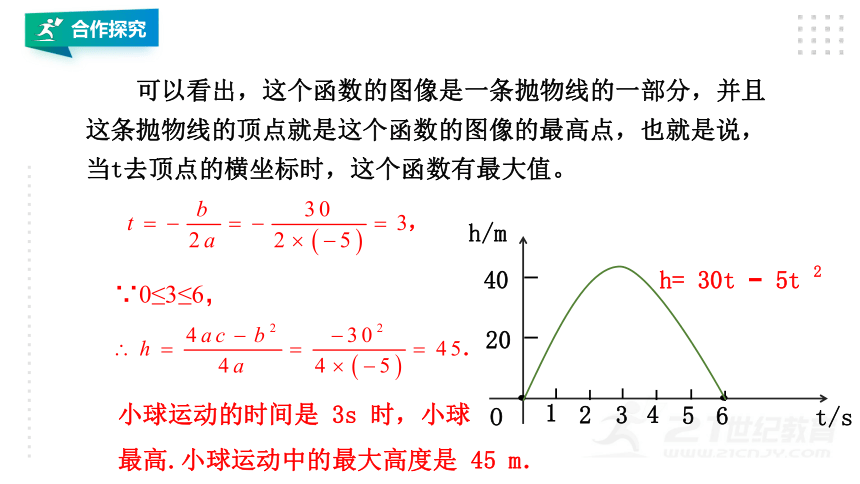
可以看出,这个函数的图像是一条抛物线的一部分,并且这条抛物线的顶点就是这个函数的图像的最高点,也就是说,当t去顶点的横坐标时,这个函数有最大值。
小球运动的时间是
3s
时,小球
最高.小球运动中的最大高度是
45
m.
∵0≤3≤6,
合作探究
例1
、
求下列函数的最大值与最小值:
x
0
y
解:
?3
1
(1)
∴当
时,y最小值=
∴当
x=1
时,
y最大值=1+3-2=2
合作探究
解:
O
x
y
1
?3
(2)
即x在对称轴的右侧.
当
时,
函数的值随着x的增大而减小.
当
时,
合作探究
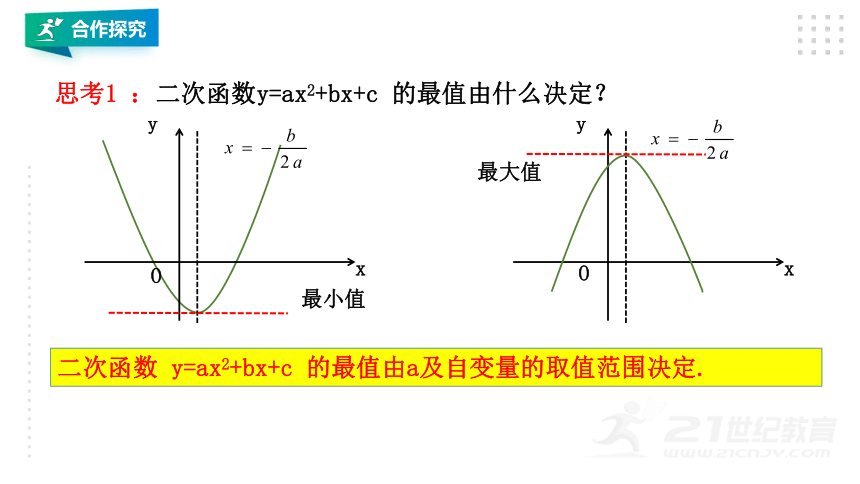
思考1
:二次函数y=ax2+bx+c
的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数
y=ax2+bx+c
的最值由a及自变量的取值范围决定.
合作探究
先判断
是否在限定范围内,若在,则二次函数在x=
时,取得最大(或小)值;若不在,则根据二次函数的增减性确定二次函数的最值.
思考2:当自变量x为全体实数时,二次函数y=ax2+bx+c的最值是多少?
当a>0时,有
,此时
.
当a<0时,有
,此时
.
思考3:当自变量x有限制时,二次函数y=ax2+bx+c的最值如何确定?
合作探究
例2
用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化.当l是多少米时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
合作探究
解:根据题意得
S=l(30?l),
即
S=-l2+30l
(0因此,当
时,S有最大值
也就是说,当l是15m时,场地的面积S最大.
合作探究
变式训练
如图,有长为24米的篱笆,一面利用墙(墙长为10m)围成长方形养鸡场.设养鸡场的长BC为x米,面积为y平方米.
请问:(1)求y与x的函数关系式及自变量x的取值范围?
(2)x取何值时所围成的面积最大,最大值是多少?
合作探究
解:(1)由题意可得:BC=xcm,AB=
cm
则y=x.
=
+12x
∵墙长为10m,
∴0<x≤10,
(2)由(1)知:
∵0<x≤10,a
<0
∴x
<12时,与随x的增大而增大;
故x=10cm时,y最大=70m2
答:当长方形的长为10m时,养鸡场的面积最大,最大面积是70m2.
合作探究
归纳总结:
二次函数解决几何面积最值问题的方法:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
综合演练
1.二次函数y=(x+2)2?3的最小值是( )
A.?2
B.?3
C.3
D.2
3.二次函数y=?2x2?4x+3(x≤?2)的最大值________.
3
4.已知直角三角形的两直角边之和为8,则该三角形的面积的最
大值是________.
B
8
2.用一根长为40
cm的绳子围成一个面积为a
cm2的长方形,那么a的值不可能为(
)
A.20
B.40
C.100
D.120
D
综合演练
5.用一根长为20
cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是______cm2.
12.5
6.用长为6米的铝合金材料做一个形状如图所示的矩形窗框.窗框的高与宽各为多少时,它的透光面积最大?最大透光面积是多少?
(铝合金型材宽度不计)
x
解:设矩形窗框的宽为x
m,则高为
m.这里应
有x>0,
故0<x<2.
透光面积y与x之间的函数关系式是:
综合演练
即
配方得
所以,当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0<x<2,这时
因此,所做矩形窗框的宽为1
m、高为1.5
m时,它的透光
面积最大,最大面积是1.5
m2.
综合演练
7.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60
cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当
x是多少时,菱形风筝面积S最大?最大面积是多少?
综合演练
∴当x=30时,S有最大值,最大值为450.
即当x为30cm时,菱形风筝的面积最大,最大面积是450cm2
。
解:
∵a
<0
课堂总结
说一说如何利用二次函数解决几何面积的最大值或者最小值问题?
本节课你有哪些收获?
作业布置
习题22.3
P51页:1、5、6
https://www.21cnjy.com/help/help_extract.php
22.3实际问题与二次函数
---几何图形的最值问题
人教版
九年级上
教学目标
1.分析实际问题中变量之间的二次函数关系.(重点)
2.会运用二次函数解决几何图形有关的最大值或最小值.
3.函数特征与几何特征的相互转化以及最值在何处取得(难点)
回顾旧知
(1)二次函数y=a(x-h)2+k的对称轴是
,顶点坐标是
.
当x=
时,y的最值是
.
(2)
二次函数y=ax2+bx+c的对称轴是
,顶点坐标是
___
.当x=
____时,函数有最值,是
_____
.
x=h
(h,k)
k
h
填空
试一试:写出下列抛物线的开口方向、对称轴、顶点坐标及其最值.
(1)y=x2?4x?5;
(配方法)
(2)y=?x2?3x+4.(公式法)
(1)开口:向上;对称轴:x=2;
顶点:(2,?9);最小值:?9.
(2)开口:向下;对称轴:x=
;顶点:(
,
);最大值:
情境导入
随着毕业季的到来,毕业生们高兴的将学士帽一起高高抛向空中,我们知道将一个物体抛向空中,时间与高度将成二次函数关系,那么你知道学士帽最多可以抛多高吗?我们一起来研究一下此类问题。
合作探究
引例:从地面竖直向上抛出一小球,小球的高度
h(单位:m)与小球的运动时间
t(单位:s)之间的关系式是
h=
30t?5t
2
(0≤t≤6).小球的运动时间是多少时,小球达到最大高度?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h=
30t
?
5t
2
【分析】我们借助函数图像解决这个问题,如图画出该函数的图像。
合作探究
t/s
h/m
O
1
2
3
4
5
6
20
40
h=
30t
?
5t
2
可以看出,这个函数的图像是一条抛物线的一部分,并且这条抛物线的顶点就是这个函数的图像的最高点,也就是说,当t去顶点的横坐标时,这个函数有最大值。
小球运动的时间是
3s
时,小球
最高.小球运动中的最大高度是
45
m.
∵0≤3≤6,
合作探究
例1
、
求下列函数的最大值与最小值:
x
0
y
解:
?3
1
(1)
∴当
时,y最小值=
∴当
x=1
时,
y最大值=1+3-2=2
合作探究
解:
O
x
y
1
?3
(2)
即x在对称轴的右侧.
当
时,
函数的值随着x的增大而减小.
当
时,
合作探究
思考1
:二次函数y=ax2+bx+c
的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数
y=ax2+bx+c
的最值由a及自变量的取值范围决定.
合作探究
先判断
是否在限定范围内,若在,则二次函数在x=
时,取得最大(或小)值;若不在,则根据二次函数的增减性确定二次函数的最值.
思考2:当自变量x为全体实数时,二次函数y=ax2+bx+c的最值是多少?
当a>0时,有
,此时
.
当a<0时,有
,此时
.
思考3:当自变量x有限制时,二次函数y=ax2+bx+c的最值如何确定?
合作探究
例2
用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化.当l是多少米时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
合作探究
解:根据题意得
S=l(30?l),
即
S=-l2+30l
(0
时,S有最大值
也就是说,当l是15m时,场地的面积S最大.
合作探究
变式训练
如图,有长为24米的篱笆,一面利用墙(墙长为10m)围成长方形养鸡场.设养鸡场的长BC为x米,面积为y平方米.
请问:(1)求y与x的函数关系式及自变量x的取值范围?
(2)x取何值时所围成的面积最大,最大值是多少?
合作探究
解:(1)由题意可得:BC=xcm,AB=
cm
则y=x.
=
+12x
∵墙长为10m,
∴0<x≤10,
(2)由(1)知:
∵0<x≤10,a
<0
∴x
<12时,与随x的增大而增大;
故x=10cm时,y最大=70m2
答:当长方形的长为10m时,养鸡场的面积最大,最大面积是70m2.
合作探究
归纳总结:
二次函数解决几何面积最值问题的方法:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
综合演练
1.二次函数y=(x+2)2?3的最小值是( )
A.?2
B.?3
C.3
D.2
3.二次函数y=?2x2?4x+3(x≤?2)的最大值________.
3
4.已知直角三角形的两直角边之和为8,则该三角形的面积的最
大值是________.
B
8
2.用一根长为40
cm的绳子围成一个面积为a
cm2的长方形,那么a的值不可能为(
)
A.20
B.40
C.100
D.120
D
综合演练
5.用一根长为20
cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是______cm2.
12.5
6.用长为6米的铝合金材料做一个形状如图所示的矩形窗框.窗框的高与宽各为多少时,它的透光面积最大?最大透光面积是多少?
(铝合金型材宽度不计)
x
解:设矩形窗框的宽为x
m,则高为
m.这里应
有x>0,
故0<x<2.
透光面积y与x之间的函数关系式是:
综合演练
即
配方得
所以,当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0<x<2,这时
因此,所做矩形窗框的宽为1
m、高为1.5
m时,它的透光
面积最大,最大面积是1.5
m2.
综合演练
7.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60
cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当
x是多少时,菱形风筝面积S最大?最大面积是多少?
综合演练
∴当x=30时,S有最大值,最大值为450.
即当x为30cm时,菱形风筝的面积最大,最大面积是450cm2
。
解:
∵a
<0
课堂总结
说一说如何利用二次函数解决几何面积的最大值或者最小值问题?
本节课你有哪些收获?
作业布置
习题22.3
P51页:1、5、6
https://www.21cnjy.com/help/help_extract.php
同课章节目录
