人教版数学七年级上册 4.3.3余角、补角的概念和性质 教案
文档属性
| 名称 | 人教版数学七年级上册 4.3.3余角、补角的概念和性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 44.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 07:37:49 | ||
图片预览

文档简介
4.3.3余角和补角
学习目标:
1、
知道余角,补角的定义,能求出一个角的余角,补角。
2、
能应用余角补角的性质进行简单的计算。
3、
感受数学与生活的密切联系,积极参与数学学习活动。
学习重点:余角补角的定义及性质。
学习难点:性质的应用
学习过程:
一、复习:?角的定义
二、新课讲解:?
1、通过学生表演,探究互为余角的定义:?
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。即:∠1是∠2的余角或∠2是∠1的余角。?
2、?通过学生表演,探究互为补角的定义:?
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。即:∠3是∠4的补角或∠4是∠3的补角。??
3、通过学生表演,探究余角补角的性质。
①等角的余角相等。
②等角的补角相等。
如图∠1?与∠2互补,∠3?与∠4互补?,如果∠1=∠3,那么∠2与∠4相等吗?为什么???
解:因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
4、通过找朋友巩固余角补角。
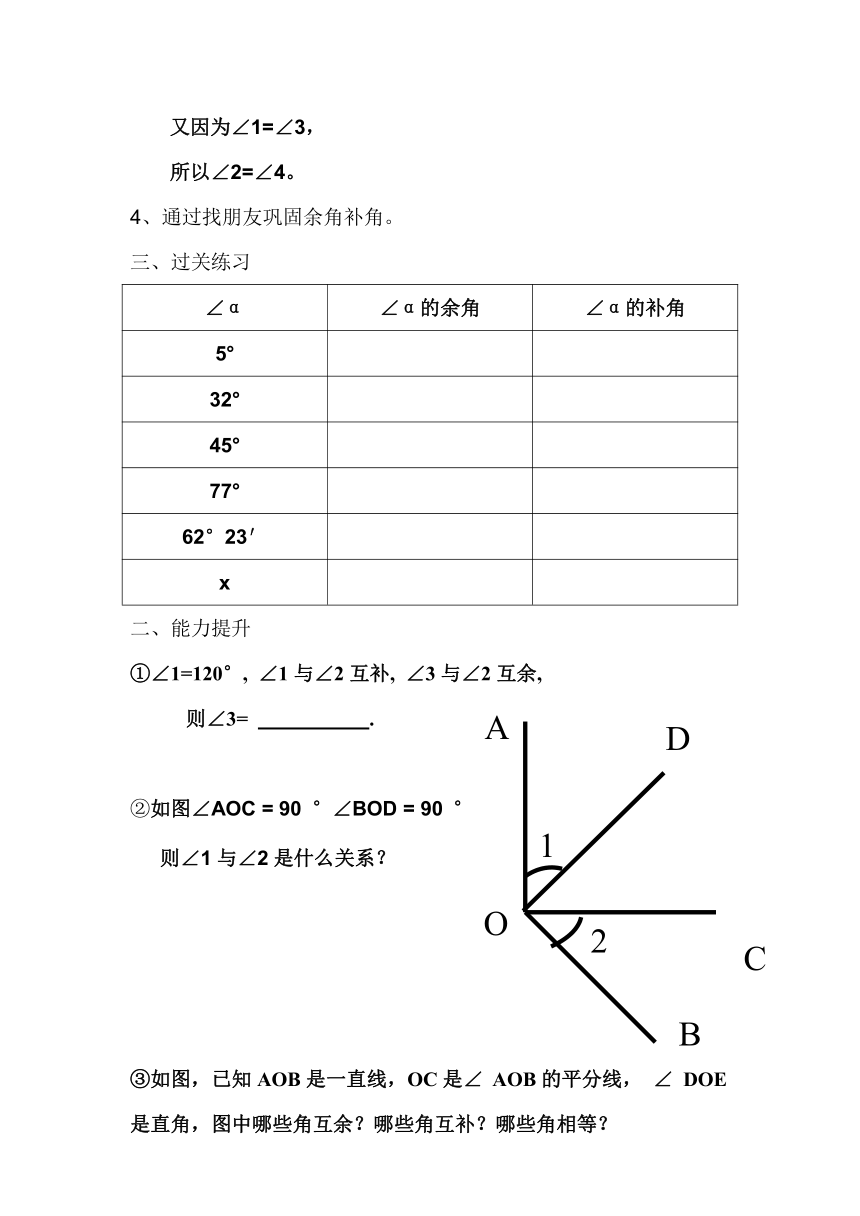
三、过关练习
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x
二、能力提升
①∠1=120°,
∠1与∠2互补,
∠3与∠2互余,
则∠3=
.
②如图∠AOC
=
90
°∠BOD
=
90
°
则∠1与∠2是什么关系?
③如图,已知AOB是一直线,OC是∠
AOB的平分线,
∠
DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
四、拓展延伸
①?若一个角的补角等于它的余角4倍,求这个角的度数。?
解:?设这个角是x?°,则它的补角是(?180°-x°),余角是(90°-x°)?。?
根据题意得:?(180-x°)=?4?(90-x°)?
???????解之得:?x?=60?
答:这个角的度数是60?°。?
?②如图,E、F是直线DG上两点,∠BEF
=
∠BFE,
∠AED
=
∠CFG
=
90
°
五、学习体会
1、
本节课你有那些收获呢?
2、
预习时的疑难解决了吗?
3、
你认为老师上课过程中还需要注意什么?
点评:课堂活动设置新颖,能体现“先学后教”的教学思想,通过“找朋友”的形式,吸引学生注意力,认知效果好。小组运用较好。
不足之处:教学过程中活动设计太多,有些过分追求教学形式而忽略了对目标的研究,教学重点略显不突出;课堂教学中缺乏必要的学法指导,各环节的教学内容缺乏连贯性。教师的点拨欠精准。
D
O
2
A
1
C
B
A
O
B
E
C
D
1
2
3
4
A
B
C
D
E
F
G
学习目标:
1、
知道余角,补角的定义,能求出一个角的余角,补角。
2、
能应用余角补角的性质进行简单的计算。
3、
感受数学与生活的密切联系,积极参与数学学习活动。
学习重点:余角补角的定义及性质。
学习难点:性质的应用
学习过程:
一、复习:?角的定义
二、新课讲解:?
1、通过学生表演,探究互为余角的定义:?
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。即:∠1是∠2的余角或∠2是∠1的余角。?
2、?通过学生表演,探究互为补角的定义:?
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。即:∠3是∠4的补角或∠4是∠3的补角。??
3、通过学生表演,探究余角补角的性质。
①等角的余角相等。
②等角的补角相等。
如图∠1?与∠2互补,∠3?与∠4互补?,如果∠1=∠3,那么∠2与∠4相等吗?为什么???
解:因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
4、通过找朋友巩固余角补角。
三、过关练习
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x
二、能力提升
①∠1=120°,
∠1与∠2互补,
∠3与∠2互余,
则∠3=
.
②如图∠AOC
=
90
°∠BOD
=
90
°
则∠1与∠2是什么关系?
③如图,已知AOB是一直线,OC是∠
AOB的平分线,
∠
DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
四、拓展延伸
①?若一个角的补角等于它的余角4倍,求这个角的度数。?
解:?设这个角是x?°,则它的补角是(?180°-x°),余角是(90°-x°)?。?
根据题意得:?(180-x°)=?4?(90-x°)?
???????解之得:?x?=60?
答:这个角的度数是60?°。?
?②如图,E、F是直线DG上两点,∠BEF
=
∠BFE,
∠AED
=
∠CFG
=
90
°
五、学习体会
1、
本节课你有那些收获呢?
2、
预习时的疑难解决了吗?
3、
你认为老师上课过程中还需要注意什么?
点评:课堂活动设置新颖,能体现“先学后教”的教学思想,通过“找朋友”的形式,吸引学生注意力,认知效果好。小组运用较好。
不足之处:教学过程中活动设计太多,有些过分追求教学形式而忽略了对目标的研究,教学重点略显不突出;课堂教学中缺乏必要的学法指导,各环节的教学内容缺乏连贯性。教师的点拨欠精准。
D
O
2
A
1
C
B
A
O
B
E
C
D
1
2
3
4
A
B
C
D
E
F
G
