2021-2022学年人教版八年级数学上册11.2.1 三角形内角和定理 同步练习-(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.2.1 三角形内角和定理 同步练习-(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 19:29:25 | ||
图片预览

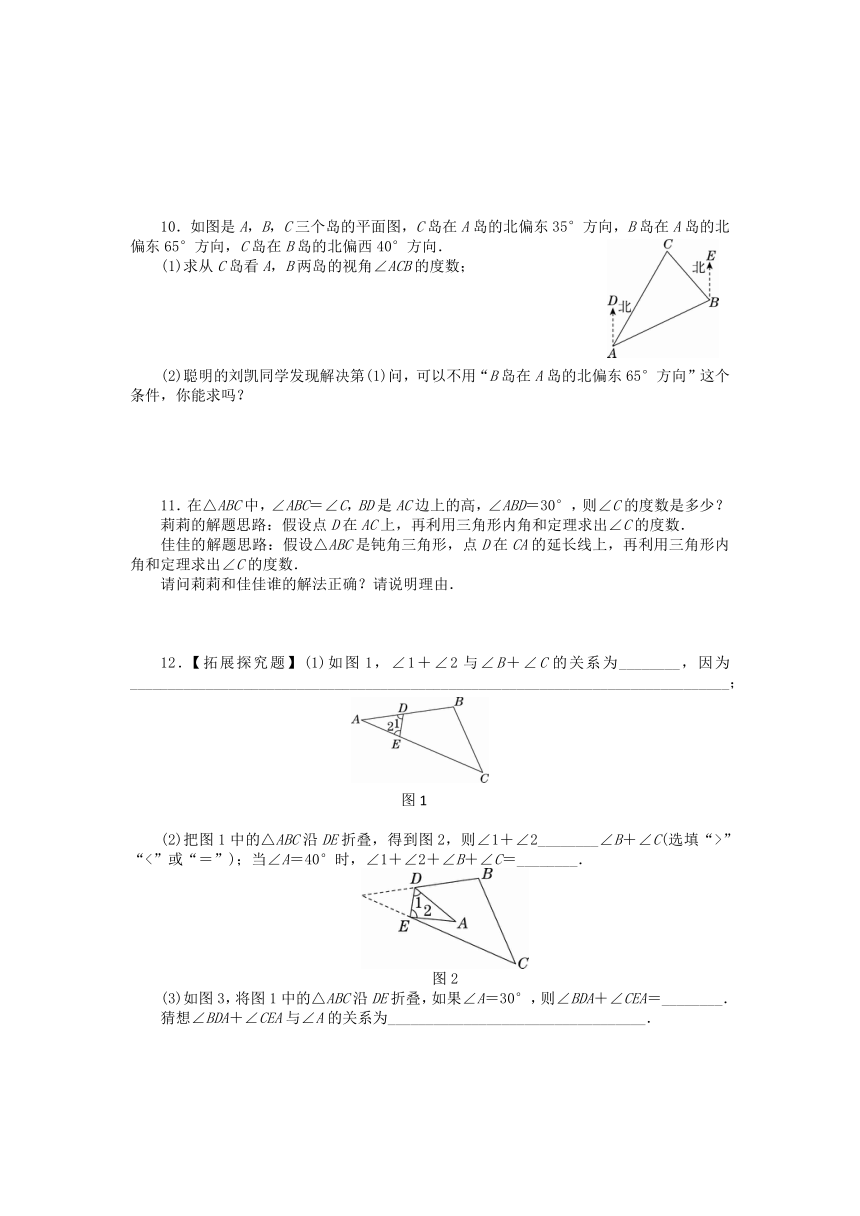
文档简介
第十一章 三角形
11.2 与三角形有关的角
第1课时 三角形的内角——三角形内角和定理
1.如图①②③④所示的四种方法中,能成为证明三角形内角和定理思路的是( )
A.①②③④
B.①③
C.③④
D.①②
2.在△ABC中,∠A=35°,∠B=80°,则∠C=( )
A.85°
B.75°
C.65°
D.55°
3.如图,在△ABC中,若∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是( )
A.50°
B.60°
C.70°
D.80°
4.如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40°
B.60°
C.70°
D.80°
5.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85°
B.80°
C.75°
D.70°
6.如图,在△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
A.100°
B.110°
C.120°
D.130°
7.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB的度数是________.
8.如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( )
A.20°
B.25°
C.35°
D.45°
9.如图,在△ABC中,已知∠B=46°,∠ACB=80°,延长BC至D,使∠CAD=∠D.求∠BAD的度数.
10.如图是A,B,C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
(1)求从C岛看A,B两岛的视角∠ACB的度数;
(2)聪明的刘凯同学发现解决第(1)问,可以不用“B岛在A岛的北偏东65°方向”这个条件,你能求吗?
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数是多少?
莉莉的解题思路:假设点D在AC上,再利用三角形内角和定理求出∠C的度数.
佳佳的解题思路:假设△ABC是钝角三角形,点D在CA的延长线上,再利用三角形内角和定理求出∠C的度数.
请问莉莉和佳佳谁的解法正确?请说明理由.
12.【拓展探究题】(1)如图1,∠1+∠2与∠B+∠C的关系为________,因为_______________________________________________________________________________;
(2)把图1中的△ABC沿DE折叠,得到图2,则∠1+∠2________∠B+∠C(选填“>”“<”或“=”);当∠A=40°时,∠1+∠2+∠B+∠C=________.
图2
(3)如图3,将图1中的△ABC沿DE折叠,如果∠A=30°,则∠BDA+∠CEA=________.
猜想∠BDA+∠CEA与∠A的关系为__________________________________.
图3
13.∠A,∠B,∠C是△ABC的三个内角.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B的度数;
14.一个零件的形状如图,按规定∠A应等于90°,∠ABD,∠ACD应分别是34°和18°.李叔叔量得∠BDC=146°,请你帮李叔叔判断这个零件是否合格,并说明理由.
参考答案
B
C
D
D
A
C
85°
B
解:∵∠ACB=80°,
∴∠ACD=180°-∠ACB=180°-80°=100°.
又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,
∴∠CAD=∠D=40°.
在△ABD中,∠BAD=180°-∠B-∠D=180°-46°-40°=94°.
10.(1)解:根据题意可知∠DAC=35°,∠DAB=65°,∠CBE=40°.∵DA∥EB,∴∠DAB+∠EBA=180°.
∴∠ABE=180°-65°=115°.
∴∠CBA=∠ABE-∠CBE=75°.
∵∠CAB=∠DAB-∠DAC=30°,
∴∠ACB=180°-∠CAB-∠CBA=75°.
(2)解:能.作CF∥AD交AB于F,则DA∥CF∥BE,
∴∠ACF=∠DAC,∠BCF=∠CBE.
∴∠ACB=∠ACF+∠BCF=35°+40°=75°.
11.解:都不正确.理由如下:①当△ABC为锐角三角形时,如图1.在△ABC中,∵BD是AC边上的高,∴∠ADB=90°.又∵∠ABD=30°,
∴∠A=180°-∠ADB-∠ABD=180°-90°-30°=60°.
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°.
又∵∠ABC=∠C,∴∠C=60°.
②当△ABC为钝角三角形时,如图2.
在直角三角形ABD中,∵∠ABD=30°,∴∠BAD=60°.
∴∠BAC=120°.又∵∠BAC+∠ABC+∠C=180°,
∴∠ABC+∠C=60°.又∵∠ABC=∠C,∴∠C=30°.
综上所述,∠C的度数是60°或30°.
12.
(1)相等
由三角形内角和定理得:
∠1+∠2+∠A=180°,∠B+∠C+∠A=180°
(2)=
280°
(3)60°
∠BDA+∠CEA=2∠A
13.
(1)解:设∠B=∠C=x°.
∵∠A+∠B+∠C=180°,∴40+x+x=180,
解得x=70.∴∠B=∠C=70°.
(2)解:设∠A=x°,∠B=y°.
∵∠A-∠B=16°,∠A+∠B+∠C=180°,∠C=54°,
∴解得
∴∠A=71°,∠B=55°.
14.
解:这个零件不合格.理由如下:
如图所示,连接BC.
在△ABC中,∠A+∠ABC+∠ACB=180°.
∵∠A=90°,∠ACD=18°,∠ABD=34°,
∴∠DCB+∠DBC=38°.
在△DCB中,∠BDC+∠DCB+∠DBC=146°+38°=184°≠180°,
∴这个零件不合格.
11.2 与三角形有关的角
第1课时 三角形的内角——三角形内角和定理
1.如图①②③④所示的四种方法中,能成为证明三角形内角和定理思路的是( )
A.①②③④
B.①③
C.③④
D.①②
2.在△ABC中,∠A=35°,∠B=80°,则∠C=( )
A.85°
B.75°
C.65°
D.55°
3.如图,在△ABC中,若∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是( )
A.50°
B.60°
C.70°
D.80°
4.如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40°
B.60°
C.70°
D.80°
5.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,则∠BDC的度数是( )
A.85°
B.80°
C.75°
D.70°
6.如图,在△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
A.100°
B.110°
C.120°
D.130°
7.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB的度数是________.
8.如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( )
A.20°
B.25°
C.35°
D.45°
9.如图,在△ABC中,已知∠B=46°,∠ACB=80°,延长BC至D,使∠CAD=∠D.求∠BAD的度数.
10.如图是A,B,C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
(1)求从C岛看A,B两岛的视角∠ACB的度数;
(2)聪明的刘凯同学发现解决第(1)问,可以不用“B岛在A岛的北偏东65°方向”这个条件,你能求吗?
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数是多少?
莉莉的解题思路:假设点D在AC上,再利用三角形内角和定理求出∠C的度数.
佳佳的解题思路:假设△ABC是钝角三角形,点D在CA的延长线上,再利用三角形内角和定理求出∠C的度数.
请问莉莉和佳佳谁的解法正确?请说明理由.
12.【拓展探究题】(1)如图1,∠1+∠2与∠B+∠C的关系为________,因为_______________________________________________________________________________;
(2)把图1中的△ABC沿DE折叠,得到图2,则∠1+∠2________∠B+∠C(选填“>”“<”或“=”);当∠A=40°时,∠1+∠2+∠B+∠C=________.
图2
(3)如图3,将图1中的△ABC沿DE折叠,如果∠A=30°,则∠BDA+∠CEA=________.
猜想∠BDA+∠CEA与∠A的关系为__________________________________.
图3
13.∠A,∠B,∠C是△ABC的三个内角.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B的度数;
14.一个零件的形状如图,按规定∠A应等于90°,∠ABD,∠ACD应分别是34°和18°.李叔叔量得∠BDC=146°,请你帮李叔叔判断这个零件是否合格,并说明理由.
参考答案
B
C
D
D
A
C
85°
B
解:∵∠ACB=80°,
∴∠ACD=180°-∠ACB=180°-80°=100°.
又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,
∴∠CAD=∠D=40°.
在△ABD中,∠BAD=180°-∠B-∠D=180°-46°-40°=94°.
10.(1)解:根据题意可知∠DAC=35°,∠DAB=65°,∠CBE=40°.∵DA∥EB,∴∠DAB+∠EBA=180°.
∴∠ABE=180°-65°=115°.
∴∠CBA=∠ABE-∠CBE=75°.
∵∠CAB=∠DAB-∠DAC=30°,
∴∠ACB=180°-∠CAB-∠CBA=75°.
(2)解:能.作CF∥AD交AB于F,则DA∥CF∥BE,
∴∠ACF=∠DAC,∠BCF=∠CBE.
∴∠ACB=∠ACF+∠BCF=35°+40°=75°.
11.解:都不正确.理由如下:①当△ABC为锐角三角形时,如图1.在△ABC中,∵BD是AC边上的高,∴∠ADB=90°.又∵∠ABD=30°,
∴∠A=180°-∠ADB-∠ABD=180°-90°-30°=60°.
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°.
又∵∠ABC=∠C,∴∠C=60°.
②当△ABC为钝角三角形时,如图2.
在直角三角形ABD中,∵∠ABD=30°,∴∠BAD=60°.
∴∠BAC=120°.又∵∠BAC+∠ABC+∠C=180°,
∴∠ABC+∠C=60°.又∵∠ABC=∠C,∴∠C=30°.
综上所述,∠C的度数是60°或30°.
12.
(1)相等
由三角形内角和定理得:
∠1+∠2+∠A=180°,∠B+∠C+∠A=180°
(2)=
280°
(3)60°
∠BDA+∠CEA=2∠A
13.
(1)解:设∠B=∠C=x°.
∵∠A+∠B+∠C=180°,∴40+x+x=180,
解得x=70.∴∠B=∠C=70°.
(2)解:设∠A=x°,∠B=y°.
∵∠A-∠B=16°,∠A+∠B+∠C=180°,∠C=54°,
∴解得
∴∠A=71°,∠B=55°.
14.
解:这个零件不合格.理由如下:
如图所示,连接BC.
在△ABC中,∠A+∠ABC+∠ACB=180°.
∵∠A=90°,∠ACD=18°,∠ABD=34°,
∴∠DCB+∠DBC=38°.
在△DCB中,∠BDC+∠DCB+∠DBC=146°+38°=184°≠180°,
∴这个零件不合格.
