人教版数学七年级上册4.3.3余角、补角的概念和性质教案(1)【教案】
文档属性
| 名称 | 人教版数学七年级上册4.3.3余角、补角的概念和性质教案(1)【教案】 |

|
|
| 格式 | zip | ||
| 文件大小 | 42.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 10:24:23 | ||
图片预览

文档简介
余角和补角
一、教学目标:
知识与技能:
(1)理解余角、补角的概念
(2)理解掌握余角和补角的性质;
(3)让学生初步接触和体会归纳演绎推理的方法和表述。
过程与方法:
(1)经历观察、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
(2)求某角的度数,使学生初步会用简单的代数思想一方程来处理图形的数量关系
情感态度价值观:
(1)类比余角的概念,同桌合作,自主探索补角的概念及特点的过程中,
培养学生合作探究精神。
(2)体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心。
二、教学重难点
重点:余角和补角的概念及其性质
难点:余角和补角的性质应用,培养学生的推理能力和有条理的表达能力。
三、教学设计
1.新课导入:
由手中的一副三角板导入新课:在一副三角尺中,每块都有一个角是90°,而其他两个角的和是90°。(30°+60°=
90°
45°+
45°=
90°)
2.新课讲授:
(1)互余的概念:
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
如右图中,
∠
1与
∠
2互为余角,
∠
1是
∠
2的余角,
∠
2也是∠
1的余角。
互余的数量关系:∠1+∠2=90
°∠1的余角
=90
°—∠1
练习:
①下面角中,哪些角互为余角?
∠1=28°
∠2=45°
∠3=68°
∠4=62°
∠5=45°
∠6=22°
②∠AOB=90°,∠1和∠2具有什么样的关系?
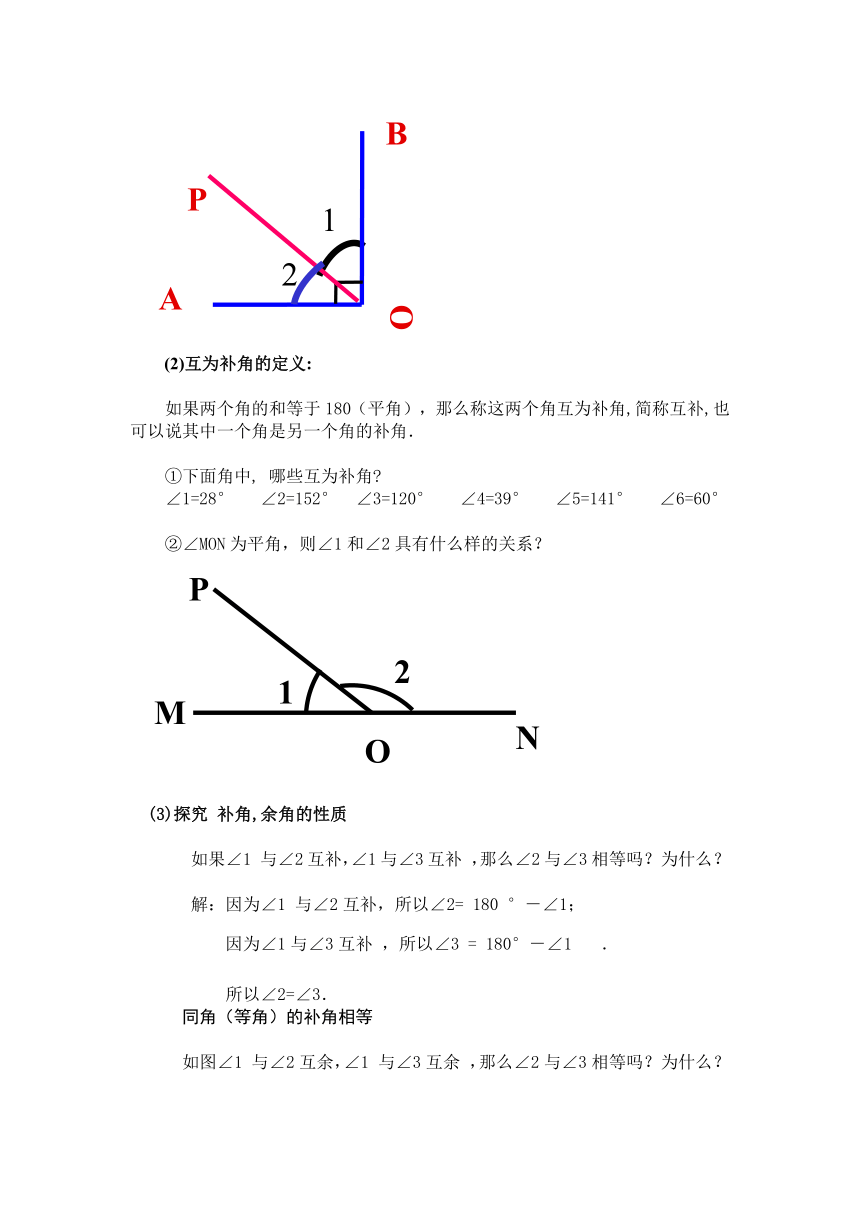
(2)互为补角的定义:
如果两个角的和等于180(平角),那么称这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
①下面角中,
哪些互为补角?
∠1=28°
∠2=152°
∠3=120°
∠4=39°
∠5=141°
∠6=60°
②∠MON为平角,则∠1和∠2具有什么样的关系?
(3)探究
补角,余角的性质
如果∠1
与∠2互补,∠1与∠3互补
,那么∠2与∠3相等吗?为什么?
解:因为∠1
与∠2互补,所以∠2=
180
°-∠1;
因为∠1与∠3互补
,所以∠3
=
180°-∠1.
所以∠2=∠3.
同角(等角)的补角相等
如图∠1
与∠2互余,∠1
与∠3互余
,那么∠2与∠3相等吗?为什么?
解:因为∠1
与∠2互余,所以∠2=90-∠1,
因为∠1与∠3互余
,所以∠3=90-∠1.
所以∠2=∠3
同角(等角)的余角相等.
3,练习
例1
如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为补角?哪些角互为余角?
例2:请认真观察下图,回答下列问题:
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?为什么?
4,小结
今天学了哪些内容?
1.互余、互补的概念:
(1)
如果两个角的和等于90°(直角),那么称这两个角互为余角;
(2)
如果两个角的和等于180°(平角)
,那么称这两个角互为补角;
2.余角、补角的性质:
(1)
同角(等角)的余角相等;
(2)
同角(等角)的补角相等.
5,作业布置:
教材138页练习1
2
3
4
板书设计
如果两个角的和等于90°(直角),那么称这两个角互为余角;
如果两个角的和等于180°(平角)
,那么称这两个角互为补角;
同角(等角)的补角相等
同角(等角)的余角相等
例1
:
∠COD
和
∠
COE
∠
AOD
和
∠BOE
∠AOD和
∠COE
∠
COD
和
∠BOE
都互为余角
2
1
3
P
A
O
B
1
2
P
M
O
N
1
2
B
A
C
D
1
2
一、教学目标:
知识与技能:
(1)理解余角、补角的概念
(2)理解掌握余角和补角的性质;
(3)让学生初步接触和体会归纳演绎推理的方法和表述。
过程与方法:
(1)经历观察、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
(2)求某角的度数,使学生初步会用简单的代数思想一方程来处理图形的数量关系
情感态度价值观:
(1)类比余角的概念,同桌合作,自主探索补角的概念及特点的过程中,
培养学生合作探究精神。
(2)体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心。
二、教学重难点
重点:余角和补角的概念及其性质
难点:余角和补角的性质应用,培养学生的推理能力和有条理的表达能力。
三、教学设计
1.新课导入:
由手中的一副三角板导入新课:在一副三角尺中,每块都有一个角是90°,而其他两个角的和是90°。(30°+60°=
90°
45°+
45°=
90°)
2.新课讲授:
(1)互余的概念:
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
如右图中,
∠
1与
∠
2互为余角,
∠
1是
∠
2的余角,
∠
2也是∠
1的余角。
互余的数量关系:∠1+∠2=90
°∠1的余角
=90
°—∠1
练习:
①下面角中,哪些角互为余角?
∠1=28°
∠2=45°
∠3=68°
∠4=62°
∠5=45°
∠6=22°
②∠AOB=90°,∠1和∠2具有什么样的关系?
(2)互为补角的定义:
如果两个角的和等于180(平角),那么称这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
①下面角中,
哪些互为补角?
∠1=28°
∠2=152°
∠3=120°
∠4=39°
∠5=141°
∠6=60°
②∠MON为平角,则∠1和∠2具有什么样的关系?
(3)探究
补角,余角的性质
如果∠1
与∠2互补,∠1与∠3互补
,那么∠2与∠3相等吗?为什么?
解:因为∠1
与∠2互补,所以∠2=
180
°-∠1;
因为∠1与∠3互补
,所以∠3
=
180°-∠1.
所以∠2=∠3.
同角(等角)的补角相等
如图∠1
与∠2互余,∠1
与∠3互余
,那么∠2与∠3相等吗?为什么?
解:因为∠1
与∠2互余,所以∠2=90-∠1,
因为∠1与∠3互余
,所以∠3=90-∠1.
所以∠2=∠3
同角(等角)的余角相等.
3,练习
例1
如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为补角?哪些角互为余角?
例2:请认真观察下图,回答下列问题:
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?为什么?
4,小结
今天学了哪些内容?
1.互余、互补的概念:
(1)
如果两个角的和等于90°(直角),那么称这两个角互为余角;
(2)
如果两个角的和等于180°(平角)
,那么称这两个角互为补角;
2.余角、补角的性质:
(1)
同角(等角)的余角相等;
(2)
同角(等角)的补角相等.
5,作业布置:
教材138页练习1
2
3
4
板书设计
如果两个角的和等于90°(直角),那么称这两个角互为余角;
如果两个角的和等于180°(平角)
,那么称这两个角互为补角;
同角(等角)的补角相等
同角(等角)的余角相等
例1
:
∠COD
和
∠
COE
∠
AOD
和
∠BOE
∠AOD和
∠COE
∠
COD
和
∠BOE
都互为余角
2
1
3
P
A
O
B
1
2
P
M
O
N
1
2
B
A
C
D
1
2
