第二章 追及和相遇问题 20张PPT
文档属性
| 名称 | 第二章 追及和相遇问题 20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 903.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览








文档简介
直线运动
相遇和追击问题
1. 相遇和追击问题的实质
2. 画出物体运动的情景图,理清三大关系
两者速度相等。它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
研究的两物体能否在相同的时刻到达相同的空间位置的问题。
(1)时间关系
(2)位移关系
(3)速度关系
3. 两种典型追击问题
(1)速度大者(匀减速)追速度小者(匀速)
①当v1=v2时,A末追上B,则A、B永不相遇,此时两者间有最小距离;
v1
a
v2
v1> v2
A
B
②当v1=v2时,A恰好追上B,则A、B相遇一次,也是避免相撞刚好追上的临界条件;
③当v1>v2时,A已追上B,则A、B相遇两次,且之后当两者速度相等时,两者间有最大距离。
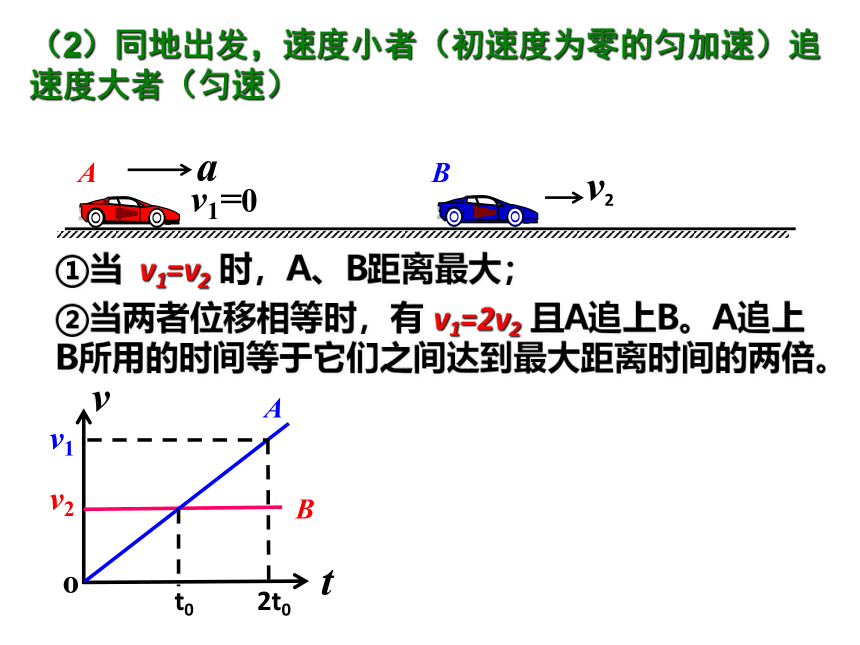
(2)同地出发,速度小者(初速度为零的匀加速)追速度大者(匀速)
①当 v1=v2 时,A、B距离最大;
②当两者位移相等时,有 v1=2v2 且A追上B。A追上
B所用的时间等于它们之间达到最大距离时间的两倍。
a
v2
A
B
v1=0
v
B
A
t
o
v2
t0
v1
2t0
4. 相遇和追击问题的常用解题方法
画出两个物体运动示意图,分析两个物体的运动性质,找出临界状态,确定它们位移、时间、速度三大关系。
(1)基本公式法——根据运动学公式,把时间关系渗透到位移关系和速度关系中列式求解。
(2)图象法——正确画出物体运动的v--t图象,根据图象的斜率、截距、面积的物理意义结合三大关系求解。
(3)相对运动法——巧妙选择参考系,简化运动过程、临界状态,根据运动学公式列式求解。注意“革命要彻底”。
(4)数学方法——根据运动学公式列出数学关系式(要有实际物理意义)利用二次函数的求根公式中Δ判别式求解。
例1. A火车以v1=20m/s速度匀速行驶,司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s速度匀速行驶,A车立即做加速度大小为a的匀减速直线运动。要使两车不相撞,a应满足什么条件?
解1:(公式法)
两车恰不相撞的条件是两车速度相同时相遇。
由A、B 速度关系:
由A、B位移关系:
(包含时间关系)
v/ms-1
B
A
t/s
o
10
t0
20
在同一个v-t图中画出A车和B车的速度时间图像图线,根据图像面积的物理意义,两车位移之差等于图中梯形的面积与矩形面积的差,当t=t0时梯形与矩形的面积之差最大,为图中阴影部分三角形的面积.根据题意,阴影部分三角形的面积不能超过100 .
物体的v-t图像的斜率表示加速度,面积表示位移。
解2:(图像法)
以B车为参照物, A车的初速度为v0=10m/s,以加速度大小a减速,行驶x=100m后“停下”,末速度为vt=0。
以B为参照物,公式中的各个量都应是相对于B的物理量.注意物理量的正负号。(革命要彻底)
解3:(相对运动法)
由于不涉及时间,所以选用速度位移公式。
代入数据得
若两车不相撞,其位移关系应为
其图像(抛物线)的顶点纵坐标必为正值,故有
解4:(二次函数极值法)
把物理问题转化为根据二次函数的极值求解的数学问题。
例2.一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始加速行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边超过汽车。试求:汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
x汽
x自
△x
解1:(公式法)
当汽车的速度与自行车的速度相等时,两车之间的距离最大。设经时间t两车之间的距离最大。则
v-t图像的斜率表示物体的加速度
当t=2s时两车的距离最大为图中阴影三角形的面积
动态分析随着时间的推移,矩形面积(自行车的位移)与三角形面积(汽车的位移)的差的变化规律
v/ms-1
自行车
汽车
t/s
o
6
t0
α
解2:(图像法)
在同一个v-t图中画出自行车和汽车的速度时间图像,根据图像面积的物理意义,两车位移之差等于图中梯形的面积与矩形面积的差,当t=t0时矩形与三角形的面积之差最大。
选自行车为参照物,以汽车相对地面的运动方向为正方向,汽车相对自行车沿反方向做匀减速运动v0=-6m/s,a=3m/s2,两车相距最远时vt=0
对汽车由公式
对汽车由公式
表示汽车相对于自行车是向后运动的,其相对于自行车的位移为向后6m.
解3:(相对运动法)
由于不涉及位移,所以选用速度公式。
由于不涉及“时间”,所以选用速度位移公式。
革命要彻底,注意物理量的正负号。
设经过时间t汽车和自行车之间的距离Δx,则
x汽
x自
△x
思考:汽车经过多少时间能追上摩托车?此时汽车的速度是多大?汽车运动的位移又是多大?
解4:(二次函数极值法)
1.甲乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m/s的速度跑完全程。乙从起跑后到接棒前的运动是匀加速的,为了确定乙起跑的时机,需在接力区前适当的位置设置标记,在某次练习中,甲在接力区前S0=13.5 m处作了标记,并以V=9m/s的速度跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒,已知接力区的长度为L=20m. 求:
(1)此次练习中乙在接棒前的加速度a; (2)在完成交接棒时乙离接力区末端的距离.
甲
乙
v
接力区
s0
L
接棒处
a
解1:(1)设经过时间t,甲追上乙,则根据位移关系
(2)在追上乙的时候,乙走的距离为
所以乙离接力区末端的距离为
再由
解2:做出甲和乙的速度时间图像
t
v/ms-1
甲
乙
t/s
o
9
α
因此
2.A、B两辆汽车在笔直的公路上同向行驶。当 B车在A车前84 m处时,B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零。A车一直以20 m/s的速度做匀速运动。经过12 s后两车相遇。问B车加速行驶的时间是多少?
解:设A车的速度为vA,B车加速行驶时间为t,两车在t0时相遇。则有
①
②
式中,t0=12s,sA 、sB分别为A、B两车相遇前行驶的路程,依题意有
③
式中,s=84m,由①②③式得解得:
④
代入题给数据vA=20 m/s,vB=4 m/s,a=2 m/s2,
得:
⑤
解得: t1=6 s,t2=18 s(t2不合题意舍去)
⑥
因此,B车加速行驶的时间为 6 s。
画出两个物体运动示意图,分析两个物体的运动性质,确定它们的位移、时间、速度三大关系。
A
B
a
例3.一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。桌布的一边与桌的AB边重合,如图。已知盘与桌布间的动摩擦因数为μ1,盘与桌面间的动摩擦因数为μ2。现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
解:设圆盘的质量为m,桌长为l,在桌布从圆盘上抽出的过程中,盘的加速度为a1,有
桌布抽出后,盘在桌面上作匀减速运动,以a2表示加速度的大小,有
盘没有从桌面上掉下的条件是
设桌布从盘下抽出所经历时间为t,在这段时间内桌布移动的距离为x,有
而
设盘刚离开桌布时的速度为v1,移动的距离为x1,离开桌布后在桌面上再运动距离x2后便停下,有
由以上各式解得
6.甲乙两车在一平直道路上同向运动,其v-t图像如图所示,图中ΔOPQ和ΔOQT的面积分别为s1和s2(s2>s1)初始时,甲车在乙车前方s0处。则( )
A.若s0=s1+s2,两车不会相遇
B.若s0C.若s0=s1,两车相遇1次
D.若s0=s2,两车相遇1次
t
v
Q
P
O
T
甲
乙
A B C
解析:由图可知甲的加速度a1比乙a2大,在达到速度相等的时间T内两车相对位移为s1。若s0=s1+s2,速度相等时甲比乙位移多s1s1),两车速度相等时还没有追上,并且甲车快、更追不上,D错。
相遇和追击问题
1. 相遇和追击问题的实质
2. 画出物体运动的情景图,理清三大关系
两者速度相等。它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
研究的两物体能否在相同的时刻到达相同的空间位置的问题。
(1)时间关系
(2)位移关系
(3)速度关系
3. 两种典型追击问题
(1)速度大者(匀减速)追速度小者(匀速)
①当v1=v2时,A末追上B,则A、B永不相遇,此时两者间有最小距离;
v1
a
v2
v1> v2
A
B
②当v1=v2时,A恰好追上B,则A、B相遇一次,也是避免相撞刚好追上的临界条件;
③当v1>v2时,A已追上B,则A、B相遇两次,且之后当两者速度相等时,两者间有最大距离。
(2)同地出发,速度小者(初速度为零的匀加速)追速度大者(匀速)
①当 v1=v2 时,A、B距离最大;
②当两者位移相等时,有 v1=2v2 且A追上B。A追上
B所用的时间等于它们之间达到最大距离时间的两倍。
a
v2
A
B
v1=0
v
B
A
t
o
v2
t0
v1
2t0
4. 相遇和追击问题的常用解题方法
画出两个物体运动示意图,分析两个物体的运动性质,找出临界状态,确定它们位移、时间、速度三大关系。
(1)基本公式法——根据运动学公式,把时间关系渗透到位移关系和速度关系中列式求解。
(2)图象法——正确画出物体运动的v--t图象,根据图象的斜率、截距、面积的物理意义结合三大关系求解。
(3)相对运动法——巧妙选择参考系,简化运动过程、临界状态,根据运动学公式列式求解。注意“革命要彻底”。
(4)数学方法——根据运动学公式列出数学关系式(要有实际物理意义)利用二次函数的求根公式中Δ判别式求解。
例1. A火车以v1=20m/s速度匀速行驶,司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s速度匀速行驶,A车立即做加速度大小为a的匀减速直线运动。要使两车不相撞,a应满足什么条件?
解1:(公式法)
两车恰不相撞的条件是两车速度相同时相遇。
由A、B 速度关系:
由A、B位移关系:
(包含时间关系)
v/ms-1
B
A
t/s
o
10
t0
20
在同一个v-t图中画出A车和B车的速度时间图像图线,根据图像面积的物理意义,两车位移之差等于图中梯形的面积与矩形面积的差,当t=t0时梯形与矩形的面积之差最大,为图中阴影部分三角形的面积.根据题意,阴影部分三角形的面积不能超过100 .
物体的v-t图像的斜率表示加速度,面积表示位移。
解2:(图像法)
以B车为参照物, A车的初速度为v0=10m/s,以加速度大小a减速,行驶x=100m后“停下”,末速度为vt=0。
以B为参照物,公式中的各个量都应是相对于B的物理量.注意物理量的正负号。(革命要彻底)
解3:(相对运动法)
由于不涉及时间,所以选用速度位移公式。
代入数据得
若两车不相撞,其位移关系应为
其图像(抛物线)的顶点纵坐标必为正值,故有
解4:(二次函数极值法)
把物理问题转化为根据二次函数的极值求解的数学问题。
例2.一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始加速行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边超过汽车。试求:汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
x汽
x自
△x
解1:(公式法)
当汽车的速度与自行车的速度相等时,两车之间的距离最大。设经时间t两车之间的距离最大。则
v-t图像的斜率表示物体的加速度
当t=2s时两车的距离最大为图中阴影三角形的面积
动态分析随着时间的推移,矩形面积(自行车的位移)与三角形面积(汽车的位移)的差的变化规律
v/ms-1
自行车
汽车
t/s
o
6
t0
α
解2:(图像法)
在同一个v-t图中画出自行车和汽车的速度时间图像,根据图像面积的物理意义,两车位移之差等于图中梯形的面积与矩形面积的差,当t=t0时矩形与三角形的面积之差最大。
选自行车为参照物,以汽车相对地面的运动方向为正方向,汽车相对自行车沿反方向做匀减速运动v0=-6m/s,a=3m/s2,两车相距最远时vt=0
对汽车由公式
对汽车由公式
表示汽车相对于自行车是向后运动的,其相对于自行车的位移为向后6m.
解3:(相对运动法)
由于不涉及位移,所以选用速度公式。
由于不涉及“时间”,所以选用速度位移公式。
革命要彻底,注意物理量的正负号。
设经过时间t汽车和自行车之间的距离Δx,则
x汽
x自
△x
思考:汽车经过多少时间能追上摩托车?此时汽车的速度是多大?汽车运动的位移又是多大?
解4:(二次函数极值法)
1.甲乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m/s的速度跑完全程。乙从起跑后到接棒前的运动是匀加速的,为了确定乙起跑的时机,需在接力区前适当的位置设置标记,在某次练习中,甲在接力区前S0=13.5 m处作了标记,并以V=9m/s的速度跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒,已知接力区的长度为L=20m. 求:
(1)此次练习中乙在接棒前的加速度a; (2)在完成交接棒时乙离接力区末端的距离.
甲
乙
v
接力区
s0
L
接棒处
a
解1:(1)设经过时间t,甲追上乙,则根据位移关系
(2)在追上乙的时候,乙走的距离为
所以乙离接力区末端的距离为
再由
解2:做出甲和乙的速度时间图像
t
v/ms-1
甲
乙
t/s
o
9
α
因此
2.A、B两辆汽车在笔直的公路上同向行驶。当 B车在A车前84 m处时,B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零。A车一直以20 m/s的速度做匀速运动。经过12 s后两车相遇。问B车加速行驶的时间是多少?
解:设A车的速度为vA,B车加速行驶时间为t,两车在t0时相遇。则有
①
②
式中,t0=12s,sA 、sB分别为A、B两车相遇前行驶的路程,依题意有
③
式中,s=84m,由①②③式得解得:
④
代入题给数据vA=20 m/s,vB=4 m/s,a=2 m/s2,
得:
⑤
解得: t1=6 s,t2=18 s(t2不合题意舍去)
⑥
因此,B车加速行驶的时间为 6 s。
画出两个物体运动示意图,分析两个物体的运动性质,确定它们的位移、时间、速度三大关系。
A
B
a
例3.一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。桌布的一边与桌的AB边重合,如图。已知盘与桌布间的动摩擦因数为μ1,盘与桌面间的动摩擦因数为μ2。现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
解:设圆盘的质量为m,桌长为l,在桌布从圆盘上抽出的过程中,盘的加速度为a1,有
桌布抽出后,盘在桌面上作匀减速运动,以a2表示加速度的大小,有
盘没有从桌面上掉下的条件是
设桌布从盘下抽出所经历时间为t,在这段时间内桌布移动的距离为x,有
而
设盘刚离开桌布时的速度为v1,移动的距离为x1,离开桌布后在桌面上再运动距离x2后便停下,有
由以上各式解得
6.甲乙两车在一平直道路上同向运动,其v-t图像如图所示,图中ΔOPQ和ΔOQT的面积分别为s1和s2(s2>s1)初始时,甲车在乙车前方s0处。则( )
A.若s0=s1+s2,两车不会相遇
B.若s0
D.若s0=s2,两车相遇1次
t
v
Q
P
O
T
甲
乙
A B C
解析:由图可知甲的加速度a1比乙a2大,在达到速度相等的时间T内两车相对位移为s1。若s0=s1+s2,速度相等时甲比乙位移多s1
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
