1.3勾股定理的应用_2021-2022学年数学北师大版八年级上册同步课时作业(word版含答案)
文档属性
| 名称 | 1.3勾股定理的应用_2021-2022学年数学北师大版八年级上册同步课时作业(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 411.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 08:24:47 | ||
图片预览


文档简介
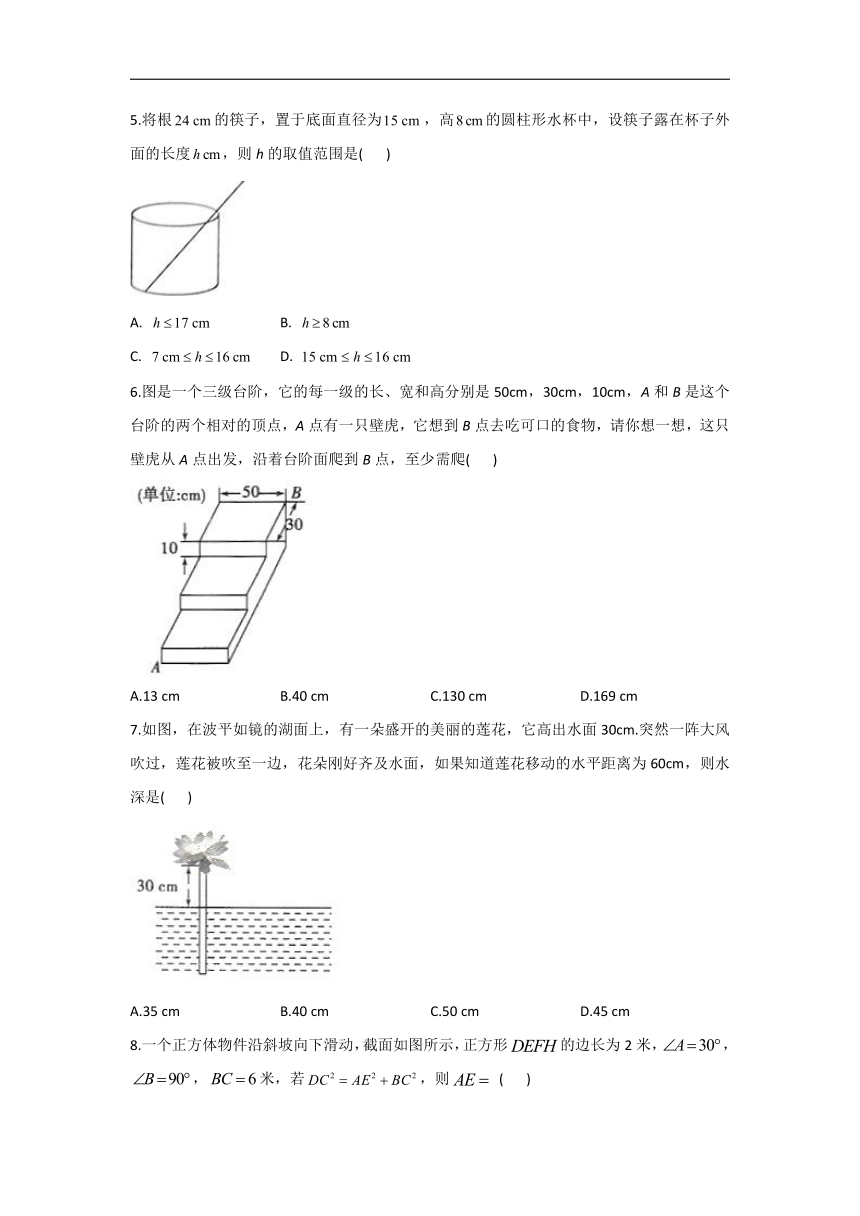
1.3勾股定理的应用—2021-2022学年数学北师大版八年级上册同步课时作业
1.校园内有两棵树,相距8米,一棵树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,则小鸟至少要飞( )
A.10米 B.11米 C.12米 D.13米
2.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度为至少要( )
A.4米 B.5米 C.6米 D.7米
3.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,梯子顶端距离地面2.4米.若梯子底端的位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
4.如图所示,台风过后某小学的旗杆在B处断裂,旗杆顶部A落在离旗杆底部C点8米处,已知旗杆长16米,则旗杆断裂的地方距底部( )
A. 4米 B. 5米 C. 6米 D. 8米
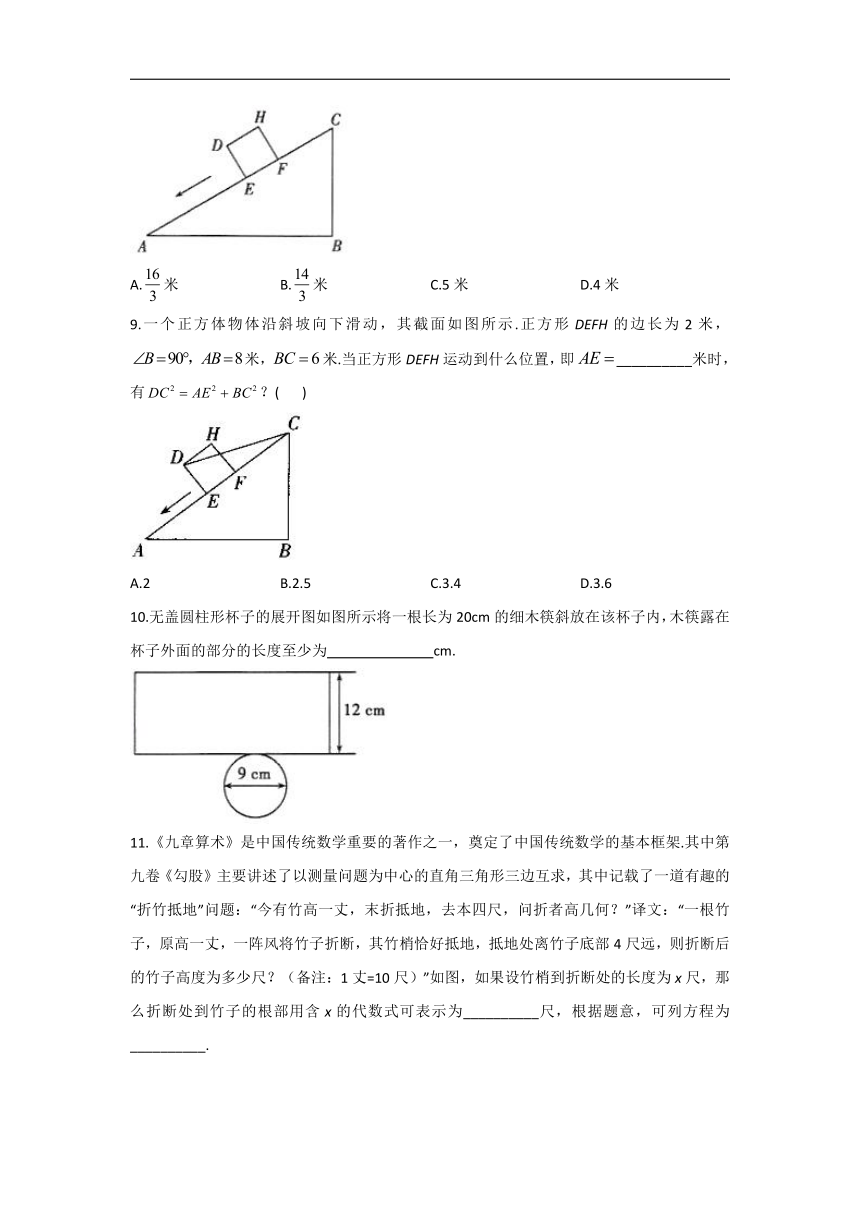
5.将根false的筷子,置于底面直径为false,高false的圆柱形水杯中,设筷子露在杯子外面的长度false,则h的取值范围是( )
A. false B. false
C. false D. false
6.图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的顶点,A点有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬( )
A.13 cm B.40 cm C.130 cm D.169 cm
7.如图,在波平如镜的湖面上,有一朵盛开的美丽的莲花,它高出水面30cm.突然一阵大风吹过,莲花被吹至一边,花朵刚好齐及水面,如果知道莲花移动的水平距离为60cm,则水深是( )
A.35 cm B.40 cm C.50 cm D.45 cm
8.一个正方体物件沿斜坡向下滑动,截面如图所示,正方形false的边长为2米,false,false,false米,若false,则false ( )
A.false米 B.false米 C.5米 D.4米
9.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,false米,false米.当正方形DEFH运动到什么位置,即false__________米时,有false?( )
A.2 B.2.5 C.3.4 D.3.6
10.无盖圆柱形杯子的展开图如图所示将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分的长度至少为 cm.
11.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,其中记载了一道有趣的“折竹抵地”问题:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”译文:“一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少尺?(备注:1丈=10尺)”如图,如果设竹梢到折断处的长度为x尺,那么折断处到竹子的根部用含x的代数式可表示为__________尺,根据题意,可列方程为__________.
12.图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若false,点A与点B的高度差false米,水平距离false米,则点C与点B的高度差CE为___________米.
13.如图,第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内,最大风力有9级(23米/秒),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动,在距离B地130km的正北方有一A地,已知A地到BC的距离false,那么台风中心经过多长时间从B点移到D点?如果在距台风中心50km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
答案以及解析
1.答案:A
解析:如图所示,AB,CD为树,且false米,false米,false米.过C作false于E,则false米,false米,在直角三角形AEC中,由勾股定理得false米,故小鸟至少要飞10米.故选A.
2.答案:D
解析:在false中,false米,故地毯的长度false米,故选D.
3.答案:A
解析:由题意可得false.在false中,false,false米.由勾股定理,得false,即false,所以false(米)(负值已舍去).所以小巷的宽度为false(米).故选A.
4.答案:C
解析:设旗杆未折断部分长为x米,则折断部分的长为false,
根据勾股定理得:false,
可得:false,即距离地面6米处断裂,
故选C.
5.答案:C
解析:首先根据圆柱的高,知筷子在杯内的最小长度是false,则在杯外的最大长度是false;
再根据勾股定理求得筷子在杯内的最大长度是(如图)false,则在杯外的最小长度是false,
所以h的取值范围是false,
故选C.
6.答案:C
解析:将台阶面展开,连接AB,如图,线段AB即为壁虎所爬的最短路线.
false,false,
在false中,根据勾股定理,得false,
所以false.
所以壁虎至少需爬130cm.
7.答案:D
解析:如图,莲花被吹至一边,花朵刚好齐及水面即线段false的长为莲花的长.
设水深为false,由题意得,false,false,false
在false中,由勾股定理得false,即false,解得false.故选D.
8.答案:B
解析:如图,连接false,设false米,
false,false,false米,
false米,false米,
false正方形false的边长为2米,false米,
falsefalse,
又false,false,
false,解得false,
因此当false时,false米故选B.
9.答案:C
解析:false米,false米,false米.设false米,则false米,false.false正方形DEFH的边长为2米,即false米,false,当false时,false,解得false,所以当false米时,有false.故选C.
10.答案:5
解析:由题意可得:杯子内的木筷长度最长为false,则木筷露在杯子外面的部分的长度至少为false.故答案为5.
11.答案:false;false
解析:由题意得竹子折断后刚好构成一个直角三角形,由竹梢到折断处的长度为x尺,得折断处到竹子根部的长度为false尺.利用勾股定理,得false.
12.答案:4.5
解析:如图,作false于F,false于G,false,
false,false,
false.在false与false中,false
false,false米.设false米,在false中,false,即false,解得false,则false(米).
13.答案:在false中,根据勾股定理,得false,
则台风中心经过false小时从B点移到D点.
如图,false距台风中心50km的圆形区域内都会受到不同程度的影响,
人们要在台风中心到达E点之前撤离,
false(小时),
正在D点休闲的游人在接到台风警报后的2.8小时内撤离才可脱离危险.
1.校园内有两棵树,相距8米,一棵树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,则小鸟至少要飞( )
A.10米 B.11米 C.12米 D.13米
2.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度为至少要( )
A.4米 B.5米 C.6米 D.7米
3.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,梯子顶端距离地面2.4米.若梯子底端的位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
4.如图所示,台风过后某小学的旗杆在B处断裂,旗杆顶部A落在离旗杆底部C点8米处,已知旗杆长16米,则旗杆断裂的地方距底部( )
A. 4米 B. 5米 C. 6米 D. 8米
5.将根false的筷子,置于底面直径为false,高false的圆柱形水杯中,设筷子露在杯子外面的长度false,则h的取值范围是( )
A. false B. false
C. false D. false
6.图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的顶点,A点有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬( )
A.13 cm B.40 cm C.130 cm D.169 cm
7.如图,在波平如镜的湖面上,有一朵盛开的美丽的莲花,它高出水面30cm.突然一阵大风吹过,莲花被吹至一边,花朵刚好齐及水面,如果知道莲花移动的水平距离为60cm,则水深是( )
A.35 cm B.40 cm C.50 cm D.45 cm
8.一个正方体物件沿斜坡向下滑动,截面如图所示,正方形false的边长为2米,false,false,false米,若false,则false ( )
A.false米 B.false米 C.5米 D.4米
9.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,false米,false米.当正方形DEFH运动到什么位置,即false__________米时,有false?( )
A.2 B.2.5 C.3.4 D.3.6
10.无盖圆柱形杯子的展开图如图所示将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分的长度至少为 cm.
11.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,其中记载了一道有趣的“折竹抵地”问题:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”译文:“一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少尺?(备注:1丈=10尺)”如图,如果设竹梢到折断处的长度为x尺,那么折断处到竹子的根部用含x的代数式可表示为__________尺,根据题意,可列方程为__________.
12.图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若false,点A与点B的高度差false米,水平距离false米,则点C与点B的高度差CE为___________米.
13.如图,第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内,最大风力有9级(23米/秒),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动,在距离B地130km的正北方有一A地,已知A地到BC的距离false,那么台风中心经过多长时间从B点移到D点?如果在距台风中心50km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
答案以及解析
1.答案:A
解析:如图所示,AB,CD为树,且false米,false米,false米.过C作false于E,则false米,false米,在直角三角形AEC中,由勾股定理得false米,故小鸟至少要飞10米.故选A.
2.答案:D
解析:在false中,false米,故地毯的长度false米,故选D.
3.答案:A
解析:由题意可得false.在false中,false,false米.由勾股定理,得false,即false,所以false(米)(负值已舍去).所以小巷的宽度为false(米).故选A.
4.答案:C
解析:设旗杆未折断部分长为x米,则折断部分的长为false,
根据勾股定理得:false,
可得:false,即距离地面6米处断裂,
故选C.
5.答案:C
解析:首先根据圆柱的高,知筷子在杯内的最小长度是false,则在杯外的最大长度是false;
再根据勾股定理求得筷子在杯内的最大长度是(如图)false,则在杯外的最小长度是false,
所以h的取值范围是false,
故选C.
6.答案:C
解析:将台阶面展开,连接AB,如图,线段AB即为壁虎所爬的最短路线.
false,false,
在false中,根据勾股定理,得false,
所以false.
所以壁虎至少需爬130cm.
7.答案:D
解析:如图,莲花被吹至一边,花朵刚好齐及水面即线段false的长为莲花的长.
设水深为false,由题意得,false,false,false
在false中,由勾股定理得false,即false,解得false.故选D.
8.答案:B
解析:如图,连接false,设false米,
false,false,false米,
false米,false米,
false正方形false的边长为2米,false米,
falsefalse,
又false,false,
false,解得false,
因此当false时,false米故选B.
9.答案:C
解析:false米,false米,false米.设false米,则false米,false.false正方形DEFH的边长为2米,即false米,false,当false时,false,解得false,所以当false米时,有false.故选C.
10.答案:5
解析:由题意可得:杯子内的木筷长度最长为false,则木筷露在杯子外面的部分的长度至少为false.故答案为5.
11.答案:false;false
解析:由题意得竹子折断后刚好构成一个直角三角形,由竹梢到折断处的长度为x尺,得折断处到竹子根部的长度为false尺.利用勾股定理,得false.
12.答案:4.5
解析:如图,作false于F,false于G,false,
false,false,
false.在false与false中,false
false,false米.设false米,在false中,false,即false,解得false,则false(米).
13.答案:在false中,根据勾股定理,得false,
则台风中心经过false小时从B点移到D点.
如图,false距台风中心50km的圆形区域内都会受到不同程度的影响,
人们要在台风中心到达E点之前撤离,
false(小时),
正在D点休闲的游人在接到台风警报后的2.8小时内撤离才可脱离危险.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
