人教版七年级上册第三章一元一次方程全章小结复习教学设计
文档属性
| 名称 | 人教版七年级上册第三章一元一次方程全章小结复习教学设计 | 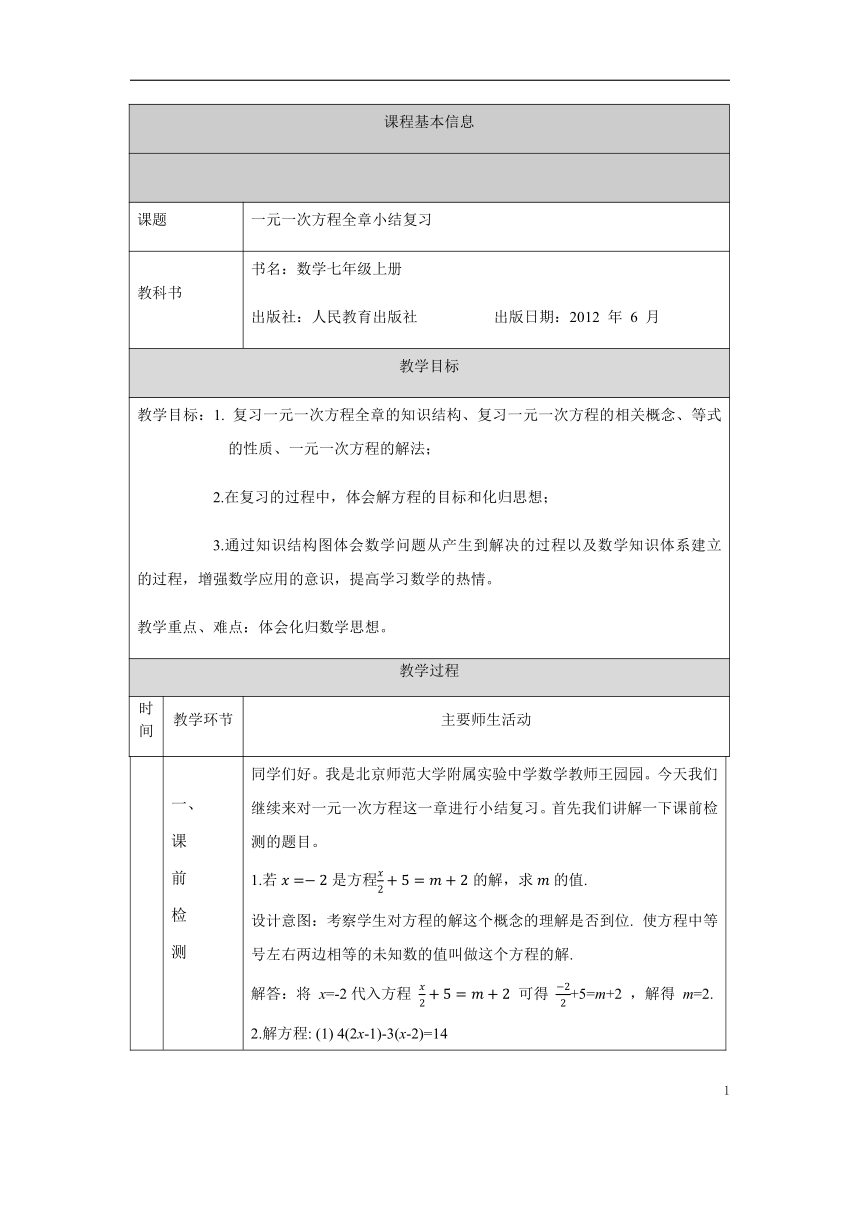 | |
| 格式 | zip | ||
| 文件大小 | 59.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 09:09:53 | ||
图片预览



文档简介
课程基本信息
课题
一元一次方程全章小结复习
教科书
书名:数学七年级上册
出版社:人民教育出版社
出版日期:2012
年
6
月
教学目标
教学目标:1.
复习一元一次方程全章的知识结构、复习一元一次方程的相关概念、等式的性质、一元一次方程的解法;
2.在复习的过程中,体会解方程的目标和化归思想;
3.通过知识结构图体会数学问题从产生到解决的过程以及数学知识体系建立的过程,增强数学应用的意识,提高学习数学的热情。
教学重点、难点:体会化归数学思想。
教学过程
时间
教学环节
主要师生活动
一、
课
前
检
测
同学们好。我是北京师范大学附属实验中学数学教师王园园。今天我们继续来对一元一次方程这一章进行小结复习。首先我们讲解一下课前检测的题目。
1.若是方程的解,求的值.
设计意图:考察学生对方程的解这个概念的理解是否到位.
使方程中等号左右两边相等的未知数的值叫做这个方程的解.
解答:将
x=-2代入方程
可得
+5=m+2
,解得
m=2.
2.解方程:
(1)
4(2x-1)-3(x-2)=14
设计意图:考察学生对一元一次方程的解法是否掌握.
讲解:
首先去括号,根据乘法分配律,得到8x-4-3x+6=14
根据等式的性质1移项,得
8
x
-3
x
=14-6+4
合并同类项,得
5
x
=12这一步依据是乘法分配律的逆用
接下来根据等式的性质2在等式两边同时除以5,将系数化为1,得到
解完一个方程后,还可以对我们求出的方程的解进行检验。
时,方程的左边为4×(2×-1)-3(
-2)=14,
方程的右边为
方程的左边和右边相等,
所以是原方程的解.
2.解方程:(2)
分析:观察发现这是一个有分数系数的一元一次方程,需要去分母。
根据等式性质2,在等式两边同时乘以3和6的最小公倍数6,
得到
2(2+1)-(5
-1)=6
去括号得4
+2-5
+1=6
移项得
4x-5x=6-2-1
合并同类项得
-x=3,
系数化为1,得
小结:通过2题(1)(2)可以看出,解方程的过程是使方程形式逐步化简,最终得出未知数的值,如。在此过程中,化归的思想方法起了重要的作用,而等式的性质及运算律是化归的依据。
3.制作一张桌子要用一个桌面和4条桌腿,
1m?木材可制作20个桌面,或者制作400条桌腿,现有12
m?木材,应用多少木材制作桌面,多少木材制作桌腿,恰好配成这种桌子多少套?
设计意图:本题考察的是列方程解应用题中的配套问题.
分析和解答:深入读题,可得到以下数量关系:
桌面数:桌腿数=1:4
桌面数=桌面所用木材×20
桌腿数=桌腿所用木材×400
桌面所用木材+
桌腿所用木材=12
依题意,列出方程
400(12-)=4×20.
解方程,得
5(12-)=,
60-5=,
-6=-60,
检验:
=10是原方程的解且符合实际意义.
答:应用10m?木材做桌面,2m?木材做桌腿,恰好配成这种桌子200套.
12分
二、
典
型
例
题
例1.解关于x的方程
=1-其中是有理数.
分析:观察这个方程,可以发现方程中有三个字母x、,但此方程是关于x的方程,解此方程就是将此方程朝x
=的形式转化.
解:去分母得3(3
x+)=6-(2x-)
去括号得
9
x+3=6-4
x+2
移项得
9
x+4
x=6+2-3
合并同类项得
13
x=6+2-3
系数化为1得
小结:1.解含多个字母的方程,首先要判断这是关于哪个字母的方程,从而分析出哪个字母是未知数,哪个字母是已知数,用含有已知数的式子表示未知数.
2.解含其它字母的关于x的方程时,仍需转化为x=的形式.
例2.当k取什么整数时,关于x的一元一次方程2kx-6=(k+2)x有整数解?
分析:这个方程中有字母x、k,但是这个方程是关于x的方程,所以方程的解是x=的形式后,再根据条件求出k的取值。
解:原方程移项得2kx
-(k+2)x=6,
合并同类项得
(k-2)x
=6,
因为是一元一次方程,所以k-20时,
方程的解为
因为x为整数,所以k-2为6的约数,即k-2
=±1,±2,±3,±6.
则k可以取-4
、-1
、0
、1
、
3、4、5、8
小结:解含除x外有其它字母的关于x的方程时,首先要关注题目对解的要求(如:整数解),同时还要关注对除x外其它字母的要求(如:
k取什么整数).
例3.我们规定:若关于x的一元一次方程的解为,则称该方程为“和解方程”.例如:方程的解为,而则方程为“和解方程”.请根据上述规定解答下列问题:
已知关于的一元一次方程是“和解方程”,求的值.
分析:面对这个新定义问题,我们需要先求一元一次方程的解,由于它是“和解方程”,同样地,我们可以根据和解方程的定义得到的值.
解:方程的解为=
.
由于是和解方程,
根据和解方程的定义可得方程的解,
解得
小结:
1.对于新定义问题,首先要读懂定义;
2.其次用不同的式子表示出方程的解,如:先解方程求出方程的解,再根据新定义中和解方程的定义得到方程的解,根据这两个表示这个方程的解的式子相等,解出相应的字母的值
3~4分
三、
课
堂
小
结
本节课主要复习的内容是:面对一个实际问题,我们可以通过设未知数,找等量关系列出一元一次方程,体现了数学的建模思想,通过去分母,去括号,移项,合并同类项,系数化1得到一元一次方程的解,解方程的过程体现着化规思想,从而通过检验得到实际问题的答案。
我们也同时学习了一元一次方程的概念,只含有一个未知数,未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。使方程中等号左右两边相等的未知数的值叫做这个方程的解
解方程的目的是得到等式中未知数的值,即将等式朝的形式转化,是一种化归的思想,转化的过程中,等式的性质、整式的运算律和运算法则是重要的依据。
2分
布置作业
见课后练习部分
1
课题
一元一次方程全章小结复习
教科书
书名:数学七年级上册
出版社:人民教育出版社
出版日期:2012
年
6
月
教学目标
教学目标:1.
复习一元一次方程全章的知识结构、复习一元一次方程的相关概念、等式的性质、一元一次方程的解法;
2.在复习的过程中,体会解方程的目标和化归思想;
3.通过知识结构图体会数学问题从产生到解决的过程以及数学知识体系建立的过程,增强数学应用的意识,提高学习数学的热情。
教学重点、难点:体会化归数学思想。
教学过程
时间
教学环节
主要师生活动
一、
课
前
检
测
同学们好。我是北京师范大学附属实验中学数学教师王园园。今天我们继续来对一元一次方程这一章进行小结复习。首先我们讲解一下课前检测的题目。
1.若是方程的解,求的值.
设计意图:考察学生对方程的解这个概念的理解是否到位.
使方程中等号左右两边相等的未知数的值叫做这个方程的解.
解答:将
x=-2代入方程
可得
+5=m+2
,解得
m=2.
2.解方程:
(1)
4(2x-1)-3(x-2)=14
设计意图:考察学生对一元一次方程的解法是否掌握.
讲解:
首先去括号,根据乘法分配律,得到8x-4-3x+6=14
根据等式的性质1移项,得
8
x
-3
x
=14-6+4
合并同类项,得
5
x
=12这一步依据是乘法分配律的逆用
接下来根据等式的性质2在等式两边同时除以5,将系数化为1,得到
解完一个方程后,还可以对我们求出的方程的解进行检验。
时,方程的左边为4×(2×-1)-3(
-2)=14,
方程的右边为
方程的左边和右边相等,
所以是原方程的解.
2.解方程:(2)
分析:观察发现这是一个有分数系数的一元一次方程,需要去分母。
根据等式性质2,在等式两边同时乘以3和6的最小公倍数6,
得到
2(2+1)-(5
-1)=6
去括号得4
+2-5
+1=6
移项得
4x-5x=6-2-1
合并同类项得
-x=3,
系数化为1,得
小结:通过2题(1)(2)可以看出,解方程的过程是使方程形式逐步化简,最终得出未知数的值,如。在此过程中,化归的思想方法起了重要的作用,而等式的性质及运算律是化归的依据。
3.制作一张桌子要用一个桌面和4条桌腿,
1m?木材可制作20个桌面,或者制作400条桌腿,现有12
m?木材,应用多少木材制作桌面,多少木材制作桌腿,恰好配成这种桌子多少套?
设计意图:本题考察的是列方程解应用题中的配套问题.
分析和解答:深入读题,可得到以下数量关系:
桌面数:桌腿数=1:4
桌面数=桌面所用木材×20
桌腿数=桌腿所用木材×400
桌面所用木材+
桌腿所用木材=12
依题意,列出方程
400(12-)=4×20.
解方程,得
5(12-)=,
60-5=,
-6=-60,
检验:
=10是原方程的解且符合实际意义.
答:应用10m?木材做桌面,2m?木材做桌腿,恰好配成这种桌子200套.
12分
二、
典
型
例
题
例1.解关于x的方程
=1-其中是有理数.
分析:观察这个方程,可以发现方程中有三个字母x、,但此方程是关于x的方程,解此方程就是将此方程朝x
=的形式转化.
解:去分母得3(3
x+)=6-(2x-)
去括号得
9
x+3=6-4
x+2
移项得
9
x+4
x=6+2-3
合并同类项得
13
x=6+2-3
系数化为1得
小结:1.解含多个字母的方程,首先要判断这是关于哪个字母的方程,从而分析出哪个字母是未知数,哪个字母是已知数,用含有已知数的式子表示未知数.
2.解含其它字母的关于x的方程时,仍需转化为x=的形式.
例2.当k取什么整数时,关于x的一元一次方程2kx-6=(k+2)x有整数解?
分析:这个方程中有字母x、k,但是这个方程是关于x的方程,所以方程的解是x=的形式后,再根据条件求出k的取值。
解:原方程移项得2kx
-(k+2)x=6,
合并同类项得
(k-2)x
=6,
因为是一元一次方程,所以k-20时,
方程的解为
因为x为整数,所以k-2为6的约数,即k-2
=±1,±2,±3,±6.
则k可以取-4
、-1
、0
、1
、
3、4、5、8
小结:解含除x外有其它字母的关于x的方程时,首先要关注题目对解的要求(如:整数解),同时还要关注对除x外其它字母的要求(如:
k取什么整数).
例3.我们规定:若关于x的一元一次方程的解为,则称该方程为“和解方程”.例如:方程的解为,而则方程为“和解方程”.请根据上述规定解答下列问题:
已知关于的一元一次方程是“和解方程”,求的值.
分析:面对这个新定义问题,我们需要先求一元一次方程的解,由于它是“和解方程”,同样地,我们可以根据和解方程的定义得到的值.
解:方程的解为=
.
由于是和解方程,
根据和解方程的定义可得方程的解,
解得
小结:
1.对于新定义问题,首先要读懂定义;
2.其次用不同的式子表示出方程的解,如:先解方程求出方程的解,再根据新定义中和解方程的定义得到方程的解,根据这两个表示这个方程的解的式子相等,解出相应的字母的值
3~4分
三、
课
堂
小
结
本节课主要复习的内容是:面对一个实际问题,我们可以通过设未知数,找等量关系列出一元一次方程,体现了数学的建模思想,通过去分母,去括号,移项,合并同类项,系数化1得到一元一次方程的解,解方程的过程体现着化规思想,从而通过检验得到实际问题的答案。
我们也同时学习了一元一次方程的概念,只含有一个未知数,未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。使方程中等号左右两边相等的未知数的值叫做这个方程的解
解方程的目的是得到等式中未知数的值,即将等式朝的形式转化,是一种化归的思想,转化的过程中,等式的性质、整式的运算律和运算法则是重要的依据。
2分
布置作业
见课后练习部分
1
