帮你归纳总结(四十):高中新课标数学考前回扣课本---三角函数、解三角形部分
文档属性
| 名称 | 帮你归纳总结(四十):高中新课标数学考前回扣课本---三角函数、解三角形部分 |

|
|
| 格式 | zip | ||
| 文件大小 | 282.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-29 00:00:00 | ||
图片预览



文档简介
帮你归纳总结(四十):高中新课标数学考前回扣课本---三角函数、解三角形部分
1. ①与(0°≤<360°)终边相同的角的集合(角与 角的终边重合):
②终边在x轴上的角的集合:
③终边在y轴上的角的集合:
④终边在坐标轴上的角的集合:
⑤终边在y=x轴上的角的集合:
⑥终边在轴上的角的集合:
⑦若角与角的终边关于x轴对称,则角与角的关系:
⑧若角与角的终边关于y轴对称,则角与角的关系:
⑨若角与角的终边在一条直线上,则角与角的关系:
⑩角与角的终边互相垂直,则角与角的关系:
2.⑴角度制与弧度制的互化:弧度,弧度,弧度
注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.
⑵ 弧长公式:;扇形面积公式:。
如:已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为 ( )
A.2 B.sin2 C. D.2sin1
如:已知扇形的周长为6 cm,面积为2 cm2,则扇形的中心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
三角函数定义:设是一个任意角,在的终边上任取(异 于原点的)一点P(x,y)P与原点的距离为r,则 ;
; .
如:已知角α的终边经过点(,-1),则角α的最小正值是( )
A. B. C. D.
如:已知角α的终边在直线3x+4y=0上,求sinα,cosα,tanα的值.
3. 单位圆中三角函数线的定义
如:若,则的大小顺序是
如:在单位圆中画出适合下列条件的角α终边的范围,并
由此写出角α的集合.
(1)sinα≥; (2)cosα≤-.
4.三角函数符号规律:一全正,二正弦,三两切,四余弦;
如:记cos(-80°)=k,那么tan100°=( )
A. B.- C. D.-
如.若sinθ>0,且sin2θ>0,则角θ的终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.诱导公式记忆规律: “函数名不(改)变,符号看象限”;即α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号;±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成 锐角时原函数值的符号.
如:化简:+;
6.同角三角函数的基本关系:;
如:已知α是三角形的内角,且sinα+cosα=, 求tanα的值。
如:若tanα=,则sinαcosα=( )
A. B. C. D.
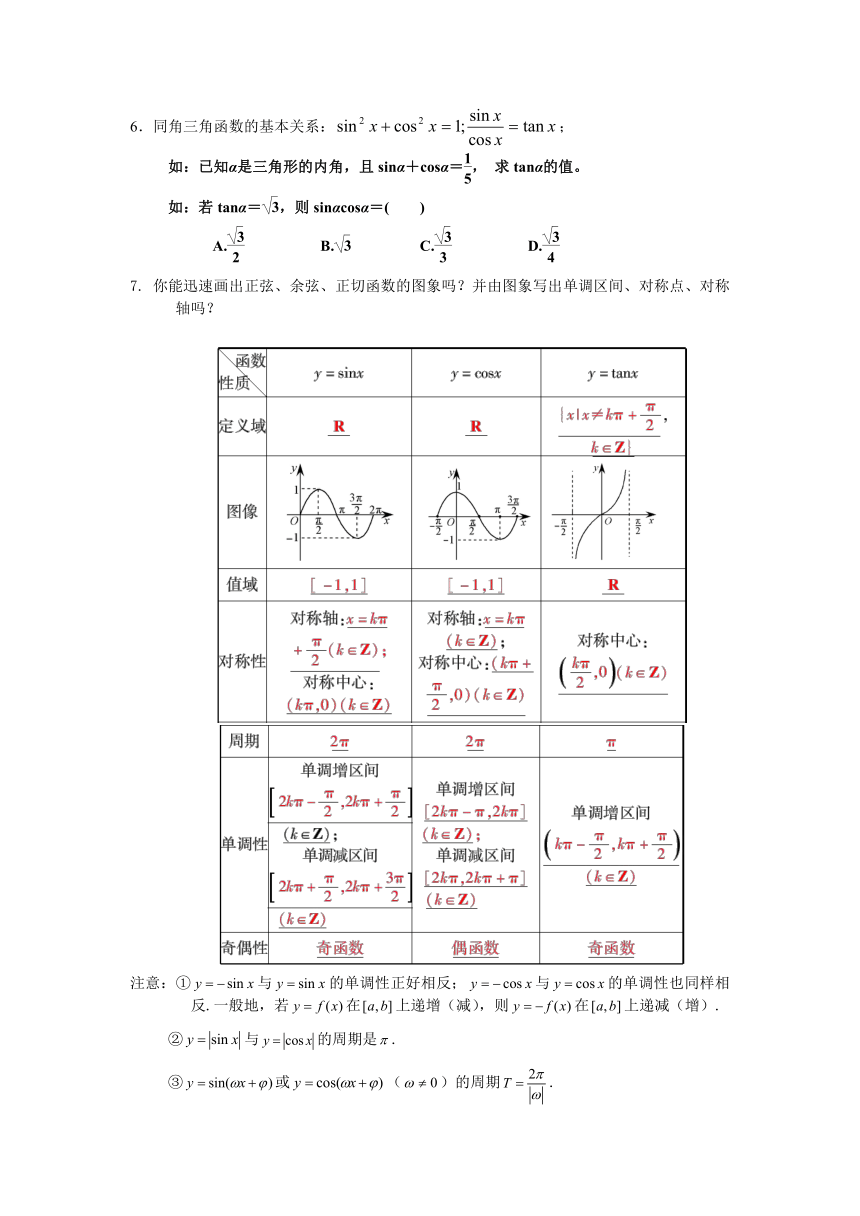
7. 你能迅速画出正弦、余弦、正切函数的图象吗?并由图象写出单调区间、对称点、对称轴吗?
注意:①与的单调性正好相反;与的单调性也同样相 反.一般地,若在上递增(减),则在上递减(增).
②与的周期是.
③或()的周期.
④的对称轴方程是(),对称中心();
的对称轴方程是(),对称中心();
的对称中心().
⑤函数在上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定 义域,为增函数,同样也是错误的].
⑥不是周期函数;为周期函数();
是周期函数(如图);为周期函数();
的周期为(如图),并非所有周期函数都有最
小正周期,例如:.
如.下列函数中,在上是增函数的是( )
A.y=sinx B.y=cosx C.y=sin2x D.y=cos2x
如。 函数y=tan的单调减区间为 .
如. 设点P是函数f(x)=sinωx(ω≠0)的图像C的一个对称中心,若点P到图像C的对
称轴的距离的最小值是,则f(x)的最小正周期是( )
A.2π B.π C. D.
8. 函数的图像和性质要熟记,
(1)振幅为_______;周期_______;
若,则为对称轴;若,则为对称点,反之也对。
(2)五点作图:令依次为, 求出与,依点(x,y)作图象。
(3)根据图像求解析式,即求的值:
如图列出,解方程组求的值.
如:函数y=sin的图像( )
A.关于点对称 B.关于直线x=对称
C.关于点对称 D.关于直线x=对称
如:电流I(A)随时间t(s)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图像如右图 所示,则当t= s时,电流是( )
A.-5 A B.5 A
C.5 A D.10 A
如:若函数y=Asin(ωx+φ)+m(A>0,ω>0)的最大值为4,最小值为0,最小正周期为
,直线x=是其图像的一条对称轴,则它的解析式是( )
A.y=4sin(4x+) B.y=2sin(2x+)+2
C.y=2sin(4x+)+2 D.y=2sin(4x+)+2
9. 熟练掌握两角和、差、倍、降幂公式及其逆向应用了吗?理解公式之间的联系:
____________________________________________。
____________________________________________
___________________, __________,_________。
___________________,
____________; ____________;
应用以上公式对三角函数式化简。(化简要求:项数最少、函数种类最少,分母中 不含三角函数,能求值,尽可能求值。)
具体方法:
(1)角的变换:如,
(2)名的变换:化弦或化切;(3)次数的变换:升、降幂公式
(4)形的变换:统一函数形式,注意运用代数运算。
(5)称为1的代换;
如:已知,求的值。
如.已知sin=,则sin2x的值为( )
A. B. C. D.
如.已知cosα=,cos(α+β)=-,且α,β∈(0,),则cos(α-β)的值等于( )
A.- B. C.- D.
如。的值是( )
A. B. C. D.
10. 在三角函数中求一个角时要注意两个方面:先求出某一个三角函数值,再判定角的范围。
如:若,求的值。
11. 在解含有正、余弦函数的问题时,你注意(到)运用函数的有界性了吗?
如:函数的值域是__________;
12. 熟练掌握三角函数图象变换了吗?(平移变换、伸缩变换)
函数y=sinx的图像经变换得到y=Asin(ωx+φ)的图像的步骤如下
方法一:
如:函数的图象经过怎样的变换才能得到的图象?
如:要得到函数y=3sin2x的图像,可将函数y=3cos的图像( )
A.沿x轴向左平移个单位长度 B.沿x轴向右平移个单位长度
C.沿x轴向左平移个单位长度 D.沿x轴向右平移个单位长度
正、余弦定理:
⑴正弦定理(是外接圆直径)
注:①;②; ③。
⑵余弦定理:等三个;注:等三个。
(3)几个公式:①三角形面积公式:;
②内切圆半径r=;③外接圆直径2R=
______;______。
如:已知圆的半径为4,a、b、c为该圆的内接三角形的三边,若abc=16,则三角 形的面积为( )
A.2 B.8 C. D.
如:要测量对岸A、B两点之间的距离,选取相距 km的C、D两点,并测得∠ACB =75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
如:在中,,
(1)求角,(2)若,求的值。
14.已知时三角形解的个数的判定:
如:在△ABC中,A=60°,a=4,b=4,则B等于( )
A.45°或135° B.135° C.45° D.以上答案都不对
A
b
a
C
h
其中h=bsinA,⑴A为锐角时:①a②a=h时,一解(直角);③h⑵A为直角或钝角时:①ab时,无解;②a>b时,一解(锐角)。
1. ①与(0°≤<360°)终边相同的角的集合(角与 角的终边重合):
②终边在x轴上的角的集合:
③终边在y轴上的角的集合:
④终边在坐标轴上的角的集合:
⑤终边在y=x轴上的角的集合:
⑥终边在轴上的角的集合:
⑦若角与角的终边关于x轴对称,则角与角的关系:
⑧若角与角的终边关于y轴对称,则角与角的关系:
⑨若角与角的终边在一条直线上,则角与角的关系:
⑩角与角的终边互相垂直,则角与角的关系:
2.⑴角度制与弧度制的互化:弧度,弧度,弧度
注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.
⑵ 弧长公式:;扇形面积公式:。
如:已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为 ( )
A.2 B.sin2 C. D.2sin1
如:已知扇形的周长为6 cm,面积为2 cm2,则扇形的中心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
三角函数定义:设是一个任意角,在的终边上任取(异 于原点的)一点P(x,y)P与原点的距离为r,则 ;
; .
如:已知角α的终边经过点(,-1),则角α的最小正值是( )
A. B. C. D.
如:已知角α的终边在直线3x+4y=0上,求sinα,cosα,tanα的值.
3. 单位圆中三角函数线的定义
如:若,则的大小顺序是
如:在单位圆中画出适合下列条件的角α终边的范围,并
由此写出角α的集合.
(1)sinα≥; (2)cosα≤-.
4.三角函数符号规律:一全正,二正弦,三两切,四余弦;
如:记cos(-80°)=k,那么tan100°=( )
A. B.- C. D.-
如.若sinθ>0,且sin2θ>0,则角θ的终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.诱导公式记忆规律: “函数名不(改)变,符号看象限”;即α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号;±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成 锐角时原函数值的符号.
如:化简:+;
6.同角三角函数的基本关系:;
如:已知α是三角形的内角,且sinα+cosα=, 求tanα的值。
如:若tanα=,则sinαcosα=( )
A. B. C. D.
7. 你能迅速画出正弦、余弦、正切函数的图象吗?并由图象写出单调区间、对称点、对称轴吗?
注意:①与的单调性正好相反;与的单调性也同样相 反.一般地,若在上递增(减),则在上递减(增).
②与的周期是.
③或()的周期.
④的对称轴方程是(),对称中心();
的对称轴方程是(),对称中心();
的对称中心().
⑤函数在上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定 义域,为增函数,同样也是错误的].
⑥不是周期函数;为周期函数();
是周期函数(如图);为周期函数();
的周期为(如图),并非所有周期函数都有最
小正周期,例如:.
如.下列函数中,在上是增函数的是( )
A.y=sinx B.y=cosx C.y=sin2x D.y=cos2x
如。 函数y=tan的单调减区间为 .
如. 设点P是函数f(x)=sinωx(ω≠0)的图像C的一个对称中心,若点P到图像C的对
称轴的距离的最小值是,则f(x)的最小正周期是( )
A.2π B.π C. D.
8. 函数的图像和性质要熟记,
(1)振幅为_______;周期_______;
若,则为对称轴;若,则为对称点,反之也对。
(2)五点作图:令依次为, 求出与,依点(x,y)作图象。
(3)根据图像求解析式,即求的值:
如图列出,解方程组求的值.
如:函数y=sin的图像( )
A.关于点对称 B.关于直线x=对称
C.关于点对称 D.关于直线x=对称
如:电流I(A)随时间t(s)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图像如右图 所示,则当t= s时,电流是( )
A.-5 A B.5 A
C.5 A D.10 A
如:若函数y=Asin(ωx+φ)+m(A>0,ω>0)的最大值为4,最小值为0,最小正周期为
,直线x=是其图像的一条对称轴,则它的解析式是( )
A.y=4sin(4x+) B.y=2sin(2x+)+2
C.y=2sin(4x+)+2 D.y=2sin(4x+)+2
9. 熟练掌握两角和、差、倍、降幂公式及其逆向应用了吗?理解公式之间的联系:
____________________________________________。
____________________________________________
___________________, __________,_________。
___________________,
____________; ____________;
应用以上公式对三角函数式化简。(化简要求:项数最少、函数种类最少,分母中 不含三角函数,能求值,尽可能求值。)
具体方法:
(1)角的变换:如,
(2)名的变换:化弦或化切;(3)次数的变换:升、降幂公式
(4)形的变换:统一函数形式,注意运用代数运算。
(5)称为1的代换;
如:已知,求的值。
如.已知sin=,则sin2x的值为( )
A. B. C. D.
如.已知cosα=,cos(α+β)=-,且α,β∈(0,),则cos(α-β)的值等于( )
A.- B. C.- D.
如。的值是( )
A. B. C. D.
10. 在三角函数中求一个角时要注意两个方面:先求出某一个三角函数值,再判定角的范围。
如:若,求的值。
11. 在解含有正、余弦函数的问题时,你注意(到)运用函数的有界性了吗?
如:函数的值域是__________;
12. 熟练掌握三角函数图象变换了吗?(平移变换、伸缩变换)
函数y=sinx的图像经变换得到y=Asin(ωx+φ)的图像的步骤如下
方法一:
如:函数的图象经过怎样的变换才能得到的图象?
如:要得到函数y=3sin2x的图像,可将函数y=3cos的图像( )
A.沿x轴向左平移个单位长度 B.沿x轴向右平移个单位长度
C.沿x轴向左平移个单位长度 D.沿x轴向右平移个单位长度
正、余弦定理:
⑴正弦定理(是外接圆直径)
注:①;②; ③。
⑵余弦定理:等三个;注:等三个。
(3)几个公式:①三角形面积公式:;
②内切圆半径r=;③外接圆直径2R=
______;______。
如:已知圆的半径为4,a、b、c为该圆的内接三角形的三边,若abc=16,则三角 形的面积为( )
A.2 B.8 C. D.
如:要测量对岸A、B两点之间的距离,选取相距 km的C、D两点,并测得∠ACB =75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
如:在中,,
(1)求角,(2)若,求的值。
14.已知时三角形解的个数的判定:
如:在△ABC中,A=60°,a=4,b=4,则B等于( )
A.45°或135° B.135° C.45° D.以上答案都不对
A
b
a
C
h
其中h=bsinA,⑴A为锐角时:①a
同课章节目录
