6.3数学归纳法_课件1(1)-湘教版数学选修2-2(34张PPT)
文档属性
| 名称 | 6.3数学归纳法_课件1(1)-湘教版数学选修2-2(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览











文档简介
1.了解数学归纳法的原理、证明的步骤及变形的特点.
2.会用数学归纳法证明有关几何问题.整除问题和归纳猜
想的问题.
数学归纳法
【课标要求】
1. 是一种证明与正整数n有关的数学命题的重要方法.用数学归纳法证明的步骤
(1)证明当n取第一个值n0时结论正确;
(2)假设当n=k(k∈N+,且k≥n0)时结论正确,证明当n= 时结论也正确.
2.在完成了这两个步骤以后,就可以断定命题对于从n0开始的所有正整数n都正确.
自学导引
数学归纳法
k+1
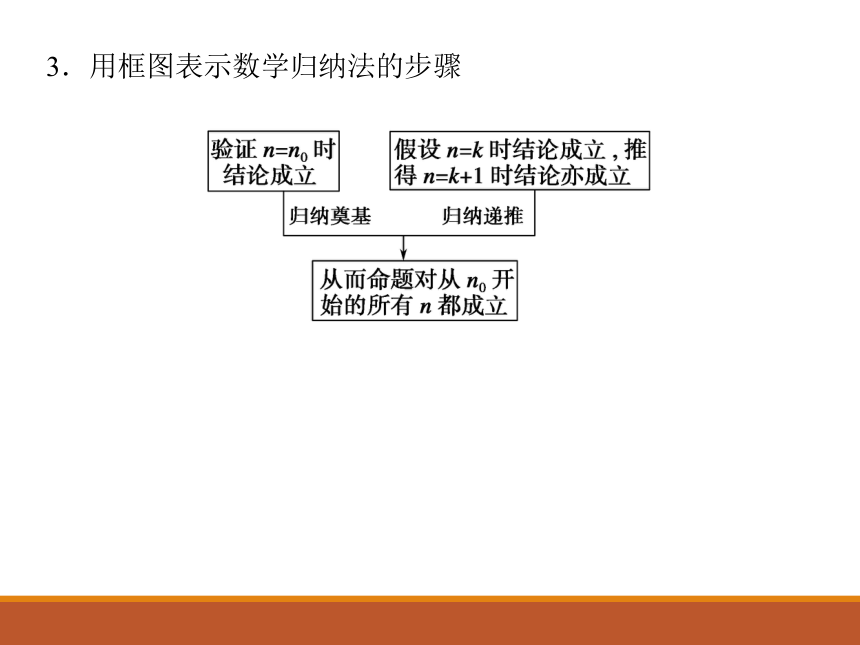
3.用框图表示数学归纳法的步骤
提示 (1)不完全归纳法:如果我们考察了某类对象中的一部分,由这一部分具有某种特征而得出该对象中的全体具有这种特征的结论为不完全归纳法.由不完全归纳法得出的结论不一定都是正确的,其正确性还需进一步证明.
(2)完全归纳法:如果我们考察了某一类对象中的所有对象而得出了该类对象全体具有某种特征的结论为完全归纳法.由完全归纳法得到的结论一定是正确的.数学归纳法是一种完全归纳法.
自主探究
1.什么是不完全归纳法和完全归纳法?
提示 验证n=n0时的n0未必是1,根据题目要求,有时可以为2,3等.
2.当n∈N+时,必须从n=1归纳吗?
答案 B
预习测评
答案 D
3.用数学归纳法证明“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取 ( ).
A.2 B.3
C.5 D.6
解析 当n取1、2、3、4时,2n>n2+1不成立,
当n=5时,25=32>52+1=26,
第一个能使2n>n2+1的n值为5,
故选C.
答案 C
4.用数学归纳法证明(1+1)(2+2)(3+3)…(n+n)=2n-1·(n2
+n)时,从n=k到n=k+1左边需要添加的因式是_______.
解析 当n=k时,左端为:(1+1)(2+2)…(k+k),
当n=k+1时,
左端为:(1+1)(2+2)…(k+k)(k+1+k+1),
由k到k+1需添加的因式为:(2k+2).
答案 2k+2
数学归纳法的步骤(1)是命题论证的基础,步骤(2)是判断命题的正确性能否递推下去的保证,这两个步骤缺一不可.如果缺少步骤(2),无法对n取n0后的数时的结论是否正确作出判断;如果缺少步骤(1)这个基础,假设就失去了成立的前提,步骤(2)就没有意义了.
(1)验证是基础
一般情况下,用数学归纳法证明与正整数有关的数学命题时,第一个允许值是命题成立的第一个正整数,并不一定所有的第一个允许值n0都是1.
要点阐释
1. 运用数学归纳法的注意点
(2)递推是关键
“假设n=k(k≥n0,k∈N+)时命题成立”这一归纳假设起着已知的作用,“n=k+1时命题成立”则是求证的目标.在证明“n=k+1时命题也成立”的过程中,必须利用归纳假设,再根据有关的定理、定义、公式、性质等数学结论推证出n=k+1时命题成立.可见数学归纳法证明的关键在于第二步.
说明:(1)数学归纳法是直接证明的一种重要方法,应用十分广泛.一般来说,与正整数有关的恒等式、不等式、数的整除性、数列的通项及前n项和等问题,都可以考虑用数学归纳法证明.
(2)归纳推理可以帮助我们发现一般规律,但是其正确性需要通过证明来验证.一般情况下,有关正整数的归纳、猜想问题,都需要由不完全归纳法得到猜想,然后用数学归纳法证明猜想是否正确.
从观察一些特殊的简单的问题入手,根据它们所体现的共同性质,运用不完全归纳法作出一般命题的猜想,然后从理论上证明(或否定)这种猜想,这个过程叫做“归纳—猜想—证明”.
这类问题涉及的知识很广泛,可以涵盖代数、三角恒等式、不等式、数列、几何问题、整除性问题等,解题一般分三步进行:
①验证p(1),p(2),p(3),p(4),…;
②提出猜想;
③用数学归纳法证明.
归纳、猜想与证明
2.
典例剖析
题型一 用数学归纳法证明等式
点评 用数学归纳法证题时,要把n=k时的命题当作条件,在证n=k+1命题成立时须用上假设.要注意当n=k+1时,等式两边的式子与n=k时等式两边的式子的联系,增加了哪些项,减少了哪些项,问题就会顺利解决.
1.用数学归纳法证明:当n∈N+时,(1·22-2·32)+(3·42-
4·52)+…+[(2n-1)(2n)2-2n(2n+1)2]=-n(n+1)(4n+3).
证明 (1)当n=1时,左式=1·22-2·32=-14,
右式=-1·2·7=-14.等式成立;
(2)假设当n=k(k∈N+)时等式成立,即
(1·22-2·32)+(3·42-4·52)+…+[(2k-1)(2k)2-2k(2k+1)2]=-k(k+1)(4k+3),
那么(1·22-2·32)+(3·42-4·52)+…+[(2k-1)(2k)2-2k(2k+1)2]+[(2k+1)(2k+2)2-(2k+2)(2k+3)2]=-k(k+1)(4k+3)-2(k+1)[(4k2+12k+9)-(4k2+6k+2)]=-k(k+1)(4k+3)-2(k+1)·(6k+7)=-(k+1)(4k2+15k+14)=-(k+1)(k+2)·(4k+7)=-(k+1)[(k+1)+1][4(k+1)+3].
这表明,当n=k+1时,等式也成立.
由(1)、(2)可知,等式对一切n∈N+都成立.
题型二 不等式的证明
点评 用数学归纳法证明不等式时,n=k+1时的目标必须清楚明确,首先分离整理出归纳假设的部分,然后明确无误地用上假设.用上假设之后,可采用综合法、分析法、比较法等方法完成后续的证明,同时注意放缩法的应用.
题型三 证明整除问题
证明 (1)当n=1时,x2n-1+y2n-1=x+y,能被x+y整除.
(2)假设当n=k(k∈N+,且k≥1)时,命题成立,即x2k-1+y2k-1能被x+y整除.
那么x2(k+1)-1+y2(k+1)-1
=x2k+1+y2k+1=x2k-1+2+y2k-1+2
=x2·x2k-1+y2·y2k-1+x2·y2k-1-x2·y2k-1
=x2(x2k-1+y2k-1)+y2k-1(y2-x2).
∵x2k-1+y2k-1能被x+y整除,y2-x2=(y+x)(y-x)也能被x+y整除,
【例3】用数学归纳法证明x2n-1+y2n-1(n∈N+)能被x+y整除.
这表明,当n=k+1时,x2(k+1)-1+y2(k+1)-1能被x+y整除.
由(1),(2)可知原命题成立.
点评 用数学归纳法证明整除性命题时,经常利用添加项的技巧来凑出假设.
证明:(1)当n=1时,62-1+1=7能被7整除.
(2)假设当n=k(k∈N+,且k≥1)时,62k-1+1能被7整除.
那么62(k+1)-1+1=62k-1+2+1
=36(62k-1+1)-35.∵62k-1+1能被7整除,35也能被7整除,
这表明,当n=k+1时,62(k+1)-1+1能被7整除.
由(1)、(2)知命题成立.
3.用数学归纳法证明62n-1+1(n∈N+)能被7整除.
【例4】在数列{an}中,a1=2,an+1=λan+λn+1+(2-λ)2n(n∈N+),其中λ>0.
(1)求a2,a3,a4;
(2)猜想{an}的通项公式并加以证明.
解 (1)由an+1=λan+λn+1+(2-λ)2n,
将a1=2代入,得a2=λa1+λ2+(2-λ)×2=λ2+4,
将a2=λ2+4代入,得a3=λa2+λ3+(2-λ)×22=2λ3+8,
将a3=2λ3+8代入,得a4=λa3+λ4+(2-λ)×23=3λ4+16.
题型四 归纳、猜想、证明
(2)由a2,a3,a4对{an}的通项公式做出猜想:an=(n-1)λn+2n.
下面用数学归纳法加以证明
当n=1时,a1=2=(1-1)λ1+21成立.
假设当n=k(k∈N+,且k≥1)时,ak=(k-1)λk+2k,
那么ak+1=λak+λk+1+(2-λ)2k=(k-1)λk+1+λ2k+λk+1+(2-λ)2k
=kλk+1+2k+1=[(k+1)-1]λk+1+2k+1.
这表明,当n=k+1时,ak+1=[(k+1)-1]λk+1+2k+1也成立.
综上可知,an=(n-1)λn+2n对任意n∈N+都成立.
点评 因为数列和数学归纳法都是与正整数有关的问题,所以利用数学归纳法研究数列问题是一种非常重要的思想方法.当数列的一般性结论(如通项公式、前n项和公式等)不易直接推出时,根据前几项归纳猜想,然后利用数学归纳法进行证明,可使问题得以顺利解决.
当k-1=0时,猜想成立,
当k-1≠0时,ak+1=(k+1)[2(k+1)-1].
这表明,当n=k+1时,结论正确.
由①、②可知,数列{an}的通项公式是an=n(2n-1)(n∈N+).
误区警示 利用数学归纳法证明时,一定要用“归纳假设”
2.会用数学归纳法证明有关几何问题.整除问题和归纳猜
想的问题.
数学归纳法
【课标要求】
1. 是一种证明与正整数n有关的数学命题的重要方法.用数学归纳法证明的步骤
(1)证明当n取第一个值n0时结论正确;
(2)假设当n=k(k∈N+,且k≥n0)时结论正确,证明当n= 时结论也正确.
2.在完成了这两个步骤以后,就可以断定命题对于从n0开始的所有正整数n都正确.
自学导引
数学归纳法
k+1
3.用框图表示数学归纳法的步骤
提示 (1)不完全归纳法:如果我们考察了某类对象中的一部分,由这一部分具有某种特征而得出该对象中的全体具有这种特征的结论为不完全归纳法.由不完全归纳法得出的结论不一定都是正确的,其正确性还需进一步证明.
(2)完全归纳法:如果我们考察了某一类对象中的所有对象而得出了该类对象全体具有某种特征的结论为完全归纳法.由完全归纳法得到的结论一定是正确的.数学归纳法是一种完全归纳法.
自主探究
1.什么是不完全归纳法和完全归纳法?
提示 验证n=n0时的n0未必是1,根据题目要求,有时可以为2,3等.
2.当n∈N+时,必须从n=1归纳吗?
答案 B
预习测评
答案 D
3.用数学归纳法证明“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取 ( ).
A.2 B.3
C.5 D.6
解析 当n取1、2、3、4时,2n>n2+1不成立,
当n=5时,25=32>52+1=26,
第一个能使2n>n2+1的n值为5,
故选C.
答案 C
4.用数学归纳法证明(1+1)(2+2)(3+3)…(n+n)=2n-1·(n2
+n)时,从n=k到n=k+1左边需要添加的因式是_______.
解析 当n=k时,左端为:(1+1)(2+2)…(k+k),
当n=k+1时,
左端为:(1+1)(2+2)…(k+k)(k+1+k+1),
由k到k+1需添加的因式为:(2k+2).
答案 2k+2
数学归纳法的步骤(1)是命题论证的基础,步骤(2)是判断命题的正确性能否递推下去的保证,这两个步骤缺一不可.如果缺少步骤(2),无法对n取n0后的数时的结论是否正确作出判断;如果缺少步骤(1)这个基础,假设就失去了成立的前提,步骤(2)就没有意义了.
(1)验证是基础
一般情况下,用数学归纳法证明与正整数有关的数学命题时,第一个允许值是命题成立的第一个正整数,并不一定所有的第一个允许值n0都是1.
要点阐释
1. 运用数学归纳法的注意点
(2)递推是关键
“假设n=k(k≥n0,k∈N+)时命题成立”这一归纳假设起着已知的作用,“n=k+1时命题成立”则是求证的目标.在证明“n=k+1时命题也成立”的过程中,必须利用归纳假设,再根据有关的定理、定义、公式、性质等数学结论推证出n=k+1时命题成立.可见数学归纳法证明的关键在于第二步.
说明:(1)数学归纳法是直接证明的一种重要方法,应用十分广泛.一般来说,与正整数有关的恒等式、不等式、数的整除性、数列的通项及前n项和等问题,都可以考虑用数学归纳法证明.
(2)归纳推理可以帮助我们发现一般规律,但是其正确性需要通过证明来验证.一般情况下,有关正整数的归纳、猜想问题,都需要由不完全归纳法得到猜想,然后用数学归纳法证明猜想是否正确.
从观察一些特殊的简单的问题入手,根据它们所体现的共同性质,运用不完全归纳法作出一般命题的猜想,然后从理论上证明(或否定)这种猜想,这个过程叫做“归纳—猜想—证明”.
这类问题涉及的知识很广泛,可以涵盖代数、三角恒等式、不等式、数列、几何问题、整除性问题等,解题一般分三步进行:
①验证p(1),p(2),p(3),p(4),…;
②提出猜想;
③用数学归纳法证明.
归纳、猜想与证明
2.
典例剖析
题型一 用数学归纳法证明等式
点评 用数学归纳法证题时,要把n=k时的命题当作条件,在证n=k+1命题成立时须用上假设.要注意当n=k+1时,等式两边的式子与n=k时等式两边的式子的联系,增加了哪些项,减少了哪些项,问题就会顺利解决.
1.用数学归纳法证明:当n∈N+时,(1·22-2·32)+(3·42-
4·52)+…+[(2n-1)(2n)2-2n(2n+1)2]=-n(n+1)(4n+3).
证明 (1)当n=1时,左式=1·22-2·32=-14,
右式=-1·2·7=-14.等式成立;
(2)假设当n=k(k∈N+)时等式成立,即
(1·22-2·32)+(3·42-4·52)+…+[(2k-1)(2k)2-2k(2k+1)2]=-k(k+1)(4k+3),
那么(1·22-2·32)+(3·42-4·52)+…+[(2k-1)(2k)2-2k(2k+1)2]+[(2k+1)(2k+2)2-(2k+2)(2k+3)2]=-k(k+1)(4k+3)-2(k+1)[(4k2+12k+9)-(4k2+6k+2)]=-k(k+1)(4k+3)-2(k+1)·(6k+7)=-(k+1)(4k2+15k+14)=-(k+1)(k+2)·(4k+7)=-(k+1)[(k+1)+1][4(k+1)+3].
这表明,当n=k+1时,等式也成立.
由(1)、(2)可知,等式对一切n∈N+都成立.
题型二 不等式的证明
点评 用数学归纳法证明不等式时,n=k+1时的目标必须清楚明确,首先分离整理出归纳假设的部分,然后明确无误地用上假设.用上假设之后,可采用综合法、分析法、比较法等方法完成后续的证明,同时注意放缩法的应用.
题型三 证明整除问题
证明 (1)当n=1时,x2n-1+y2n-1=x+y,能被x+y整除.
(2)假设当n=k(k∈N+,且k≥1)时,命题成立,即x2k-1+y2k-1能被x+y整除.
那么x2(k+1)-1+y2(k+1)-1
=x2k+1+y2k+1=x2k-1+2+y2k-1+2
=x2·x2k-1+y2·y2k-1+x2·y2k-1-x2·y2k-1
=x2(x2k-1+y2k-1)+y2k-1(y2-x2).
∵x2k-1+y2k-1能被x+y整除,y2-x2=(y+x)(y-x)也能被x+y整除,
【例3】用数学归纳法证明x2n-1+y2n-1(n∈N+)能被x+y整除.
这表明,当n=k+1时,x2(k+1)-1+y2(k+1)-1能被x+y整除.
由(1),(2)可知原命题成立.
点评 用数学归纳法证明整除性命题时,经常利用添加项的技巧来凑出假设.
证明:(1)当n=1时,62-1+1=7能被7整除.
(2)假设当n=k(k∈N+,且k≥1)时,62k-1+1能被7整除.
那么62(k+1)-1+1=62k-1+2+1
=36(62k-1+1)-35.∵62k-1+1能被7整除,35也能被7整除,
这表明,当n=k+1时,62(k+1)-1+1能被7整除.
由(1)、(2)知命题成立.
3.用数学归纳法证明62n-1+1(n∈N+)能被7整除.
【例4】在数列{an}中,a1=2,an+1=λan+λn+1+(2-λ)2n(n∈N+),其中λ>0.
(1)求a2,a3,a4;
(2)猜想{an}的通项公式并加以证明.
解 (1)由an+1=λan+λn+1+(2-λ)2n,
将a1=2代入,得a2=λa1+λ2+(2-λ)×2=λ2+4,
将a2=λ2+4代入,得a3=λa2+λ3+(2-λ)×22=2λ3+8,
将a3=2λ3+8代入,得a4=λa3+λ4+(2-λ)×23=3λ4+16.
题型四 归纳、猜想、证明
(2)由a2,a3,a4对{an}的通项公式做出猜想:an=(n-1)λn+2n.
下面用数学归纳法加以证明
当n=1时,a1=2=(1-1)λ1+21成立.
假设当n=k(k∈N+,且k≥1)时,ak=(k-1)λk+2k,
那么ak+1=λak+λk+1+(2-λ)2k=(k-1)λk+1+λ2k+λk+1+(2-λ)2k
=kλk+1+2k+1=[(k+1)-1]λk+1+2k+1.
这表明,当n=k+1时,ak+1=[(k+1)-1]λk+1+2k+1也成立.
综上可知,an=(n-1)λn+2n对任意n∈N+都成立.
点评 因为数列和数学归纳法都是与正整数有关的问题,所以利用数学归纳法研究数列问题是一种非常重要的思想方法.当数列的一般性结论(如通项公式、前n项和公式等)不易直接推出时,根据前几项归纳猜想,然后利用数学归纳法进行证明,可使问题得以顺利解决.
当k-1=0时,猜想成立,
当k-1≠0时,ak+1=(k+1)[2(k+1)-1].
这表明,当n=k+1时,结论正确.
由①、②可知,数列{an}的通项公式是an=n(2n-1)(n∈N+).
误区警示 利用数学归纳法证明时,一定要用“归纳假设”
同课章节目录
