第6章 推理与证明 复习课件-湘教版数学选修2-2(47张PPT)
文档属性
| 名称 | 第6章 推理与证明 复习课件-湘教版数学选修2-2(47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览










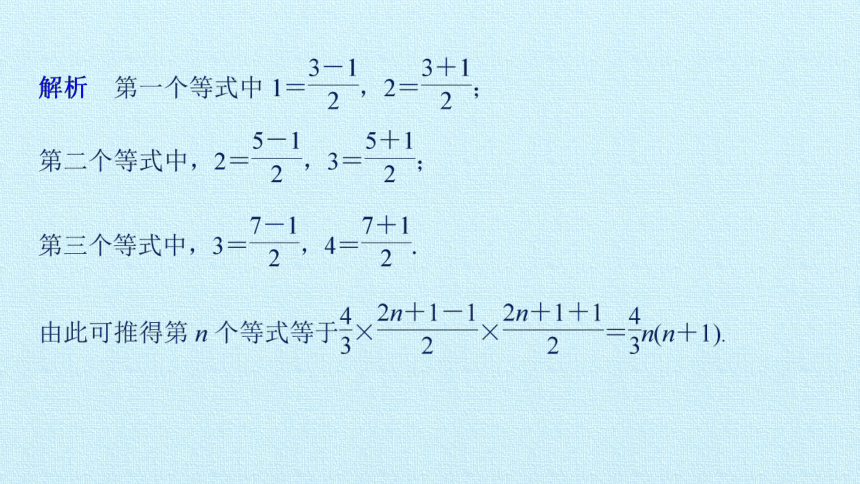
文档简介
第6章 推理与证明
复习课件
学习目标
1.整合本章知识要点.
2.进一步理解合情推理与演绎推理的概念、思维形式、应用等.
3.进一步熟练掌握直接证明与间接证明.
4.理解数学归纳法,并会用数学归纳法证明问题.
知识梳理
达标检测
题型探究
内容索引
知识梳理
1.合情推理
(1)归纳推理:由 到 、由 到 的推理.
(2)类比推理:由 到 的推理.
(3)合情推理:归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
部分
整体
个别
一般
特殊
特殊
2.演绎推理
(1)演绎推理:由 到 的推理.
(2)“三段论”是演绎推理的一般模式,包括:
① ——已知的一般原理;
② ——所研究的特殊情况;
③ ——根据一般原理,对特殊情况做出的判断.
一般
特殊
大前提
小前提
结论
3.直接证明和间接证明
(1)直接证明的两类基本方法是 和 :
① 是从已知条件推出结论的证明方法;
② 是从结论追溯到条件的证明方法.
(2)间接证明的一种方法是 ,是从结论反面成立出发,推出矛盾的方法.
4.数学归纳法
数学归纳法主要用于解决与正整数有关的数学命题.证明时,它的两个步骤缺一不可,它的第一步(归纳奠基)是证当n= 时结论成立;第二步(归纳递推)是假设当n= 时结论成立,推得当n= 时结论也成立.
综合法
分析法
综合法
分析法
反证法
n0
k+1
k
1.归纳推理得到的结论不一定正确,类比推理得到的结论一定正确.
( )
2.“所有3的倍数都是9的倍数,某数m是3的倍数,则m一定是9的倍数”,这是三段论推理,但其结论是错误的.( )
3.综合法是直接证明,分析法是间接证明.( )
4.反证法是指将结论和条件同时否定,推出矛盾.( )
[思考辨析 判断正误]
×
×
√
×
题型探究
类型一 合情推理与演绎推理
例1 (1)观察下列等式:
……
照此规律,
答案
解析
答案
解析
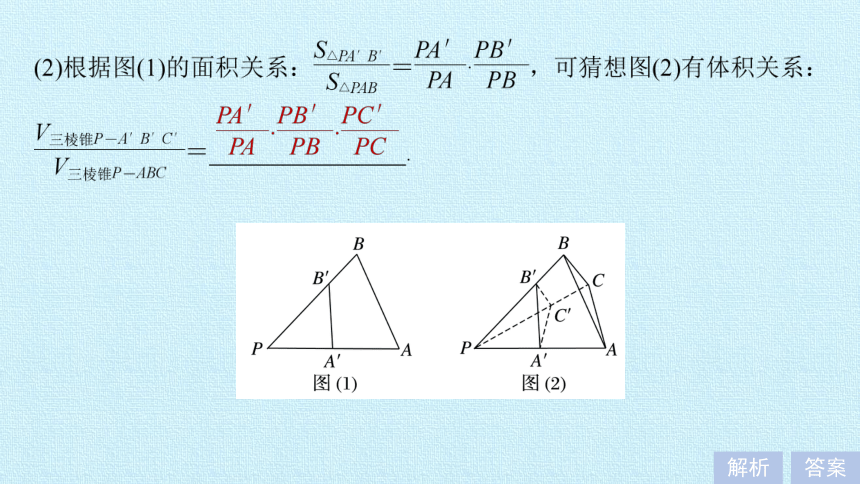
解析 题干两图中,与△PAB,△PA′B′相对应的是三棱锥P-ABC,P-A′B′C′;
与△PA′B′两边PA′,PB′相对应的是三棱锥P-A′B′C′的三条侧棱PA′,PB′,PC′.
与△PAB的两条边PA,PB相对应的是三棱锥P-ABC的三条侧棱PA,PB,PC.
答案
解析
(3)有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是______.
解析 由题意可知丙不拿2和3.
若丙拿1和2,则乙拿2和3,甲拿1和3,满足题意;
若丙拿1和3,则乙拿2和3,甲拿1和2,不满足题意.
故甲的卡片上的数字是1和3.
1和3
反思与感悟 (1)用归纳推理可从具体事例中发现一般规律,但应注意,仅根据一系列有限的特殊事例,所得出的一般结论不一定可靠,其结论的正确与否,还要经过严格的理论证明.
(2)进行类比推理时,要尽量从本质上思考,不要被表面现象所迷惑,否则,只抓住一点表面的相似甚至假象就去类比,就会犯机械类比的错误.
(3)演绎推理是由一般到特殊的推理,其结论不会超出前提所界定的范围,所以其前提和结论之间的联系是必然的.因此,在演绎推理中,只要前提及推理正确,结论必然正确.
跟踪训练1 (1)如图是由火柴棒拼成的图形,第n个图形由n个正方形组成.
?
通过观察可以发现:第4个图形中有____根火柴棒;第n个图形中有_______根火柴棒.
解析 设第n个图形中火柴棒的根数为an,可知a4=13.
通过观察得到递推关系式an-an-1=3(n≥2,n∈N*),
所以an=3n+1.
答案
解析
13
3n+1
(2)若数列{an}为等差数列,Sn为其前n项和,则有性质“若Sm=Sn(m,n∈N*且m≠n),则Sm+n=0.”类比上述性质,相应地,当数列{bn}为等比数列时,写出一个正确的性质:____________________________________________ _______________________________.
解析 由等差数列的运算性质类比推理到等比数列的运算性质时,
加减运算类比推理为乘除运算.
累加类比为累乘,
由此,等差数列{an}的性质类比到等比数列{bn}中为:
数列{bn}为等比数列,Tm表示其前m项的积,
若Tm=Tn(m,n∈N*,m≠n),则Tm+n=1.
数列{bn}为等比数列,Tm表示其前m项的积,若Tm=Tn(m,n∈N*,m≠n),则Tm+n=1
答案
解析
类型二 综合法与分析法
证明
证明 方法一 分析法
∵α∈(0,π),∴sin α>0,
∵1-cos α>0,
∴4cos α(1-cos α)≤1,
可变形为4cos2α-4cos α+1≥0,
只需证(2cos α-1)2≥0,显然成立.
方法二 综合法
∵α∈(0,π),∴sin α>0,
反思与感悟 分析法和综合法是两种思路相反的推理方法:分析法是倒溯,综合法是顺推,二者各有优缺点.分析法容易探路,且探路与表述合一,缺点是表述易错;综合法条件清晰,易于表述,因此对于难题常把二者交互运用,互补优缺,形成分析综合法,其逻辑基础是充分条件与必要条件.
跟踪训练2 设a,b是两个正实数,且a≠b,求证:a3+b3>a2b+ab2.
证明 要证a3+b3>a2b+ab2成立,即需证
(a+b)(a2-ab+b2)>ab(a+b)成立,
即需证a2-ab+b2>ab成立.
只需证a2-2ab+b2>0成立,
即需证(a-b)2>0成立.
而由已知条件可知,a≠b,所以a-b≠0,
所以(a-b)2>0显然成立.
即a3+b3>a2b+ab2.
证明
类型三 反证法
证明
因为x>0且y>0,
所以1+x≥2y且1+y≥2x,
两式相加,得2+x+y≥2x+2y,所以x+y≤2.
这与已知x+y>2矛盾.
反思与感悟 反证法常用于直接证明困难或以否定形式出现的命题;涉及“都是……”“都不是……”“至少……”“至多……”等形式的命题时,也常用反证法.
跟踪训练3 已知:ac≥2(b+d).
求证:方程x2+ax+b=0与方程x2+cx+d=0中至少有一个方程有实数根.
证明 假设两方程都没有实数根,
则Δ1=a2-4b<0与Δ2=c2-4d<0,有a2+c2<4(b+d),而a2+c2≥2ac,
从而有4(b+d)>2ac,即ac<2(b+d),与已知矛盾,故原命题成立.
证明
类型四 数学归纳法
解答
下面用数学归纳法证明:
(2)假设当n=k(k≥1,k∈N*)时猜想成立,
那么当n=k+1时,
即当n=k+1时猜想成立.
由(1)(2)可知,对任意正整数n,猜想均成立.
反思与感悟 (1)用数学归纳法证明等式问题是数学归纳法的常见题型,其关键点在于“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始n0是多少.
(2)由n=k到n=k+1时,除等式两边变化的项外还要利用当n=k时的式子,即利用假设,正确写出归纳证明的步骤,从而使问题得以证明.
跟踪训练4 观察下列四个等式:
第一个式子 1=1
第二个式子 2+3+4=9
第三个式子 3+4+5+6+7=25
第四个式子 4+5+6+7+8+9+10=49
(1)按照此规律,写出第五个等式;
解 第5个等式:5+6+7+…+13=81.
解答
(2)请你做出一般性的猜想,并用数学归纳法证明.
解答
解 猜想第n个等式为
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2.
下面用数学归纳法证明.
①当n=1时,左边=1,右边=(2-1)2=1,
猜想成立.
②假设当n=k(k≥1,k∈N*)时,猜想成立,
即有k+(k+1)+(k+2)+…+(3k-2)=(2k-1)2.
那么当n=k+1时,
左边=(k+1)+(k+2)+…+(3k-2)+(3k-1)+3k+(3k+1)
=k+(k+1)+(k+2)+…+(3k-2)+(2k-1)+3k+(3k+1)
=(2k-1)2+(2k-1)+3k+(3k+1)
=4k2-4k+1+8k=(2k+1)2
=[2(k+1)-1]2.
右边=[2(k+1)-1]2,
即当n=k+1时,猜想也成立.
根据①②知,猜想对任意n∈N*都成立.
达标检测
1.数列5,9,17,33,x,…中的x等于
A.47 B.65
C.63 D.128
解析 5=22+1,9=23+1,17=24+1,33=25+1,
归纳可得:x=26+1=65.
√
1
2
3
4
5
答案
解析
解析
1
2
3
4
5
答案
√
1
2
3
4
5
1
2
3
4
5
解析
答案
√
3.若a>0,b>0,则有
解析
4.用反证法证明命题:“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是
A.方程x3+ax+b=0没有实根
B.方程x3+ax+b=0至多有一个实数
C.方程x3+ax+b=0至多有两个实根
D.方程x3+ax+b=0恰好有两个实根
解析 方程x3+ax+b=0至少有一个实根的反面是方程x3+ax+b=0没有实根,故选A.
1
2
3
4
5
答案
√
解答
1
2
3
4
5
左边=右边,所以等式成立.
(2)假设当n=k(k≥1,k∈N*)时等式成立,
则当n=k+1时,
1
2
3
4
5
1
2
3
4
5
所以当n=k+1时,等式也成立,
由(1)(2)可知,对于一切n∈N*,等式都成立.
1.归纳和类比都是合情推理,前者是由特殊到一般,部分到整体的推理,后者是由特殊到特殊的推理,但二者都能由已知推测未知,都能用于猜想,推理的结论不一定为真,有待进一步证明.
2.演绎推理与合情推理不同,是由一般到特殊的推理,是数学中证明的基本推理形式.也是公理化体系所采用的推理形式,另一方面,合情推理与演绎推理又是相辅相成的,前者是后者的前提,后者论证前者的可靠性.
规律与方法
3.直接证明和间接证明是数学证明的两类基本证明方法.直接证明的两类基本方法是综合法和分析法:综合法是从已知条件推导出结论的证明方法;分析法是由结论追溯到条件的证明方法,在解决数学问题时,常把它们结合起来使用,间接证法的一种方法是反证法,反证法是从结论反面成立出发,推出矛盾的证明方法.
4.数学归纳法主要用于解决与正整数有关的数学问题.证明时,它的两个步骤缺一不可.它的第一步(归纳奠基)当n=n0时,结论成立.第二步(归纳递推)假设当n=k时,结论成立,推得当n=k+1时,结论也成立.数学归纳法是在可靠的基础上,利用命题自身具有的传递性,运用有限的步骤(两步)证明出无限的命题成立.
谢 谢
复习课件
学习目标
1.整合本章知识要点.
2.进一步理解合情推理与演绎推理的概念、思维形式、应用等.
3.进一步熟练掌握直接证明与间接证明.
4.理解数学归纳法,并会用数学归纳法证明问题.
知识梳理
达标检测
题型探究
内容索引
知识梳理
1.合情推理
(1)归纳推理:由 到 、由 到 的推理.
(2)类比推理:由 到 的推理.
(3)合情推理:归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
部分
整体
个别
一般
特殊
特殊
2.演绎推理
(1)演绎推理:由 到 的推理.
(2)“三段论”是演绎推理的一般模式,包括:
① ——已知的一般原理;
② ——所研究的特殊情况;
③ ——根据一般原理,对特殊情况做出的判断.
一般
特殊
大前提
小前提
结论
3.直接证明和间接证明
(1)直接证明的两类基本方法是 和 :
① 是从已知条件推出结论的证明方法;
② 是从结论追溯到条件的证明方法.
(2)间接证明的一种方法是 ,是从结论反面成立出发,推出矛盾的方法.
4.数学归纳法
数学归纳法主要用于解决与正整数有关的数学命题.证明时,它的两个步骤缺一不可,它的第一步(归纳奠基)是证当n= 时结论成立;第二步(归纳递推)是假设当n= 时结论成立,推得当n= 时结论也成立.
综合法
分析法
综合法
分析法
反证法
n0
k+1
k
1.归纳推理得到的结论不一定正确,类比推理得到的结论一定正确.
( )
2.“所有3的倍数都是9的倍数,某数m是3的倍数,则m一定是9的倍数”,这是三段论推理,但其结论是错误的.( )
3.综合法是直接证明,分析法是间接证明.( )
4.反证法是指将结论和条件同时否定,推出矛盾.( )
[思考辨析 判断正误]
×
×
√
×
题型探究
类型一 合情推理与演绎推理
例1 (1)观察下列等式:
……
照此规律,
答案
解析
答案
解析
解析 题干两图中,与△PAB,△PA′B′相对应的是三棱锥P-ABC,P-A′B′C′;
与△PA′B′两边PA′,PB′相对应的是三棱锥P-A′B′C′的三条侧棱PA′,PB′,PC′.
与△PAB的两条边PA,PB相对应的是三棱锥P-ABC的三条侧棱PA,PB,PC.
答案
解析
(3)有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是______.
解析 由题意可知丙不拿2和3.
若丙拿1和2,则乙拿2和3,甲拿1和3,满足题意;
若丙拿1和3,则乙拿2和3,甲拿1和2,不满足题意.
故甲的卡片上的数字是1和3.
1和3
反思与感悟 (1)用归纳推理可从具体事例中发现一般规律,但应注意,仅根据一系列有限的特殊事例,所得出的一般结论不一定可靠,其结论的正确与否,还要经过严格的理论证明.
(2)进行类比推理时,要尽量从本质上思考,不要被表面现象所迷惑,否则,只抓住一点表面的相似甚至假象就去类比,就会犯机械类比的错误.
(3)演绎推理是由一般到特殊的推理,其结论不会超出前提所界定的范围,所以其前提和结论之间的联系是必然的.因此,在演绎推理中,只要前提及推理正确,结论必然正确.
跟踪训练1 (1)如图是由火柴棒拼成的图形,第n个图形由n个正方形组成.
?
通过观察可以发现:第4个图形中有____根火柴棒;第n个图形中有_______根火柴棒.
解析 设第n个图形中火柴棒的根数为an,可知a4=13.
通过观察得到递推关系式an-an-1=3(n≥2,n∈N*),
所以an=3n+1.
答案
解析
13
3n+1
(2)若数列{an}为等差数列,Sn为其前n项和,则有性质“若Sm=Sn(m,n∈N*且m≠n),则Sm+n=0.”类比上述性质,相应地,当数列{bn}为等比数列时,写出一个正确的性质:____________________________________________ _______________________________.
解析 由等差数列的运算性质类比推理到等比数列的运算性质时,
加减运算类比推理为乘除运算.
累加类比为累乘,
由此,等差数列{an}的性质类比到等比数列{bn}中为:
数列{bn}为等比数列,Tm表示其前m项的积,
若Tm=Tn(m,n∈N*,m≠n),则Tm+n=1.
数列{bn}为等比数列,Tm表示其前m项的积,若Tm=Tn(m,n∈N*,m≠n),则Tm+n=1
答案
解析
类型二 综合法与分析法
证明
证明 方法一 分析法
∵α∈(0,π),∴sin α>0,
∵1-cos α>0,
∴4cos α(1-cos α)≤1,
可变形为4cos2α-4cos α+1≥0,
只需证(2cos α-1)2≥0,显然成立.
方法二 综合法
∵α∈(0,π),∴sin α>0,
反思与感悟 分析法和综合法是两种思路相反的推理方法:分析法是倒溯,综合法是顺推,二者各有优缺点.分析法容易探路,且探路与表述合一,缺点是表述易错;综合法条件清晰,易于表述,因此对于难题常把二者交互运用,互补优缺,形成分析综合法,其逻辑基础是充分条件与必要条件.
跟踪训练2 设a,b是两个正实数,且a≠b,求证:a3+b3>a2b+ab2.
证明 要证a3+b3>a2b+ab2成立,即需证
(a+b)(a2-ab+b2)>ab(a+b)成立,
即需证a2-ab+b2>ab成立.
只需证a2-2ab+b2>0成立,
即需证(a-b)2>0成立.
而由已知条件可知,a≠b,所以a-b≠0,
所以(a-b)2>0显然成立.
即a3+b3>a2b+ab2.
证明
类型三 反证法
证明
因为x>0且y>0,
所以1+x≥2y且1+y≥2x,
两式相加,得2+x+y≥2x+2y,所以x+y≤2.
这与已知x+y>2矛盾.
反思与感悟 反证法常用于直接证明困难或以否定形式出现的命题;涉及“都是……”“都不是……”“至少……”“至多……”等形式的命题时,也常用反证法.
跟踪训练3 已知:ac≥2(b+d).
求证:方程x2+ax+b=0与方程x2+cx+d=0中至少有一个方程有实数根.
证明 假设两方程都没有实数根,
则Δ1=a2-4b<0与Δ2=c2-4d<0,有a2+c2<4(b+d),而a2+c2≥2ac,
从而有4(b+d)>2ac,即ac<2(b+d),与已知矛盾,故原命题成立.
证明
类型四 数学归纳法
解答
下面用数学归纳法证明:
(2)假设当n=k(k≥1,k∈N*)时猜想成立,
那么当n=k+1时,
即当n=k+1时猜想成立.
由(1)(2)可知,对任意正整数n,猜想均成立.
反思与感悟 (1)用数学归纳法证明等式问题是数学归纳法的常见题型,其关键点在于“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始n0是多少.
(2)由n=k到n=k+1时,除等式两边变化的项外还要利用当n=k时的式子,即利用假设,正确写出归纳证明的步骤,从而使问题得以证明.
跟踪训练4 观察下列四个等式:
第一个式子 1=1
第二个式子 2+3+4=9
第三个式子 3+4+5+6+7=25
第四个式子 4+5+6+7+8+9+10=49
(1)按照此规律,写出第五个等式;
解 第5个等式:5+6+7+…+13=81.
解答
(2)请你做出一般性的猜想,并用数学归纳法证明.
解答
解 猜想第n个等式为
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2.
下面用数学归纳法证明.
①当n=1时,左边=1,右边=(2-1)2=1,
猜想成立.
②假设当n=k(k≥1,k∈N*)时,猜想成立,
即有k+(k+1)+(k+2)+…+(3k-2)=(2k-1)2.
那么当n=k+1时,
左边=(k+1)+(k+2)+…+(3k-2)+(3k-1)+3k+(3k+1)
=k+(k+1)+(k+2)+…+(3k-2)+(2k-1)+3k+(3k+1)
=(2k-1)2+(2k-1)+3k+(3k+1)
=4k2-4k+1+8k=(2k+1)2
=[2(k+1)-1]2.
右边=[2(k+1)-1]2,
即当n=k+1时,猜想也成立.
根据①②知,猜想对任意n∈N*都成立.
达标检测
1.数列5,9,17,33,x,…中的x等于
A.47 B.65
C.63 D.128
解析 5=22+1,9=23+1,17=24+1,33=25+1,
归纳可得:x=26+1=65.
√
1
2
3
4
5
答案
解析
解析
1
2
3
4
5
答案
√
1
2
3
4
5
1
2
3
4
5
解析
答案
√
3.若a>0,b>0,则有
解析
4.用反证法证明命题:“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是
A.方程x3+ax+b=0没有实根
B.方程x3+ax+b=0至多有一个实数
C.方程x3+ax+b=0至多有两个实根
D.方程x3+ax+b=0恰好有两个实根
解析 方程x3+ax+b=0至少有一个实根的反面是方程x3+ax+b=0没有实根,故选A.
1
2
3
4
5
答案
√
解答
1
2
3
4
5
左边=右边,所以等式成立.
(2)假设当n=k(k≥1,k∈N*)时等式成立,
则当n=k+1时,
1
2
3
4
5
1
2
3
4
5
所以当n=k+1时,等式也成立,
由(1)(2)可知,对于一切n∈N*,等式都成立.
1.归纳和类比都是合情推理,前者是由特殊到一般,部分到整体的推理,后者是由特殊到特殊的推理,但二者都能由已知推测未知,都能用于猜想,推理的结论不一定为真,有待进一步证明.
2.演绎推理与合情推理不同,是由一般到特殊的推理,是数学中证明的基本推理形式.也是公理化体系所采用的推理形式,另一方面,合情推理与演绎推理又是相辅相成的,前者是后者的前提,后者论证前者的可靠性.
规律与方法
3.直接证明和间接证明是数学证明的两类基本证明方法.直接证明的两类基本方法是综合法和分析法:综合法是从已知条件推导出结论的证明方法;分析法是由结论追溯到条件的证明方法,在解决数学问题时,常把它们结合起来使用,间接证法的一种方法是反证法,反证法是从结论反面成立出发,推出矛盾的证明方法.
4.数学归纳法主要用于解决与正整数有关的数学问题.证明时,它的两个步骤缺一不可.它的第一步(归纳奠基)当n=n0时,结论成立.第二步(归纳递推)假设当n=k时,结论成立,推得当n=k+1时,结论也成立.数学归纳法是在可靠的基础上,利用命题自身具有的传递性,运用有限的步骤(两步)证明出无限的命题成立.
谢 谢
同课章节目录
