4.3.2 函数的极大值和极小值 课件-湘教版数学选修2-2(16张PPT)
文档属性
| 名称 | 4.3.2 函数的极大值和极小值 课件-湘教版数学选修2-2(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 679.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览





文档简介
4.3.2 函数的极大值和极小值
天高云淡,望断南飞雁。不到长城非好汉,屈指行程二万。六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?大家熟悉的毛主席翻越六盘山时的咏怀之作,生活在六盘山脚下的我们,更为熟悉它的连绵起伏,形成许多的山峰与山谷,函数图象在上升下降的转折点处形成“峰”与“谷”,即函数的极值与导数。
情景导入
问题1 : “山峰”顶端的高度与其附近的高度有什么关系?“山峰”从左到右有什么样的变化趋势?如何用导数描述它的这种变化趋势?
新课探究
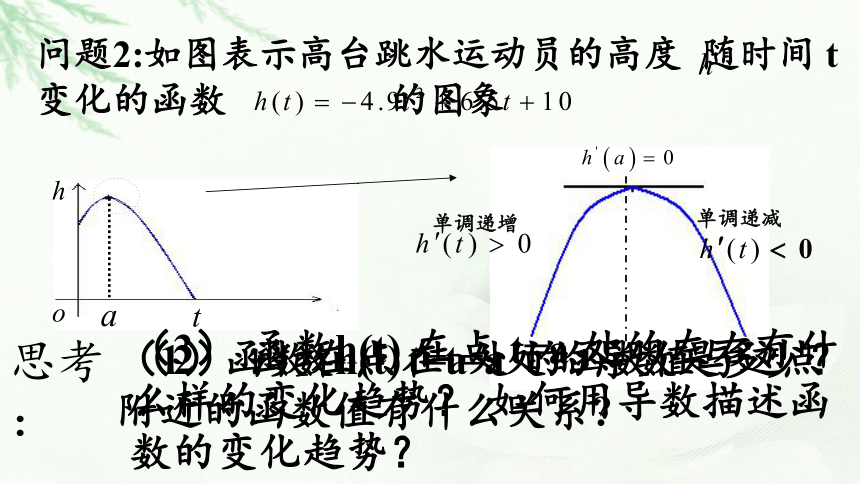
问题2:如图表示高台跳水运动员的高度 随时间 t变化的函数 的图象
单调递增
单调递减
(3) 函数h(t) 在点 t=a 处的左右有什么样的变化趋势? 如何用导数描述函数的变化趋势?
(1)函数在点 t=a处 的函数值与这点附近的函数值有什么关系?
(2) 函数h(t)在t=a处的导数是多少?
思考:
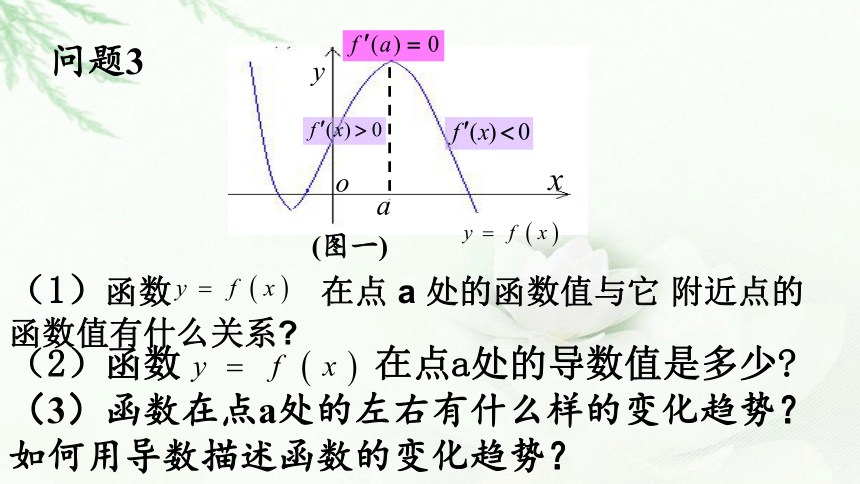
(3)函数在点a处的左右有什么样的变化趋势? 如何用导数描述函数的变化趋势?
(1)函数 在点 a 处的函数值与它 附近点的函数值有什么关系?
(2)函数 在点a处的导数值是多少?
问题3
(图一)
我们就说f(a)是函数y=f(x)的一个极大值.
点a叫做极大值点.
1 极大值的定义
函数y=f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都大,
f′(a)=0 ,
且在点x=a附近的左侧f′(x)>0,右侧f′ (x)<0
思考! 请同学们类比极大值的定义,给出极小值的定义。
我们就说f(b)是函数y=f(x)的一个极小值.
点b叫做极小值点.
2 极小值的定义
函数y=f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都小,
f′(b)=0 ,
且在点x=b附近的左侧f′(x)<0,右侧f′ (x)>0
极小值点、极大值点统称极值点,
极大值和极小值统称为极值.
思考:极大值一定大于极小值吗?
【牛刀小试!】指出哪些是极大值点, 哪些是极大值.哪些是极小值点,哪些是极小值?
极大值点:d,a,h
极小值点c,e,g
极大值:f(d),f(a),f(h)
a
极小值:f(c),f(e),f(g)
2、极值是一个局部的性质,在整定义域内可能有多个极值点
1、极大值与极小值没有必然关系,极大值可能比极小值还小.
【知识归纳:】
例1:求函数 的极值.
【例题讲解】
【方法归纳】求函数极值的一般步骤:
求导—求极点—列表—求极值
左负右正为极小值,左正右负为极大值。
(1)确定定义域并求导;
(2)令f’(x)=0并求出方程的根;
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
【课堂探究】
f?(x0) =0 x0 是可导函数f(x)的极值点
注意:f /(x0)=0是函数取得极值的必要不充分条件
导数值为0的点一定是函数的极值点吗?
【巩固练习1】观察下图并回答问题
(1)如图是函数 的图象,试找出函数
的极值点,并指出哪些是极大值点,哪些是极小值点?
(2)如果把函数图象改为导函数 的图象?
求函数 的极值
【巩固练习2】
一、极值的概念
二、用导数法求极值的步骤
(1)确定函数的定义域
(2)求导数f'(x)
(3)求方程f'(x) =0的全部解
(4)检查f'(x)在f'(x) =0的根左.右两边值的符号,如果左正右负(或左负右正),那么f(x)在这个根取得极大值或极小值
三、通过本节课使我们学会了应用数形结合法去求函数极值
课堂小结
谢 谢
天高云淡,望断南飞雁。不到长城非好汉,屈指行程二万。六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?大家熟悉的毛主席翻越六盘山时的咏怀之作,生活在六盘山脚下的我们,更为熟悉它的连绵起伏,形成许多的山峰与山谷,函数图象在上升下降的转折点处形成“峰”与“谷”,即函数的极值与导数。
情景导入
问题1 : “山峰”顶端的高度与其附近的高度有什么关系?“山峰”从左到右有什么样的变化趋势?如何用导数描述它的这种变化趋势?
新课探究
问题2:如图表示高台跳水运动员的高度 随时间 t变化的函数 的图象
单调递增
单调递减
(3) 函数h(t) 在点 t=a 处的左右有什么样的变化趋势? 如何用导数描述函数的变化趋势?
(1)函数在点 t=a处 的函数值与这点附近的函数值有什么关系?
(2) 函数h(t)在t=a处的导数是多少?
思考:
(3)函数在点a处的左右有什么样的变化趋势? 如何用导数描述函数的变化趋势?
(1)函数 在点 a 处的函数值与它 附近点的函数值有什么关系?
(2)函数 在点a处的导数值是多少?
问题3
(图一)
我们就说f(a)是函数y=f(x)的一个极大值.
点a叫做极大值点.
1 极大值的定义
函数y=f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都大,
f′(a)=0 ,
且在点x=a附近的左侧f′(x)>0,右侧f′ (x)<0
思考! 请同学们类比极大值的定义,给出极小值的定义。
我们就说f(b)是函数y=f(x)的一个极小值.
点b叫做极小值点.
2 极小值的定义
函数y=f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都小,
f′(b)=0 ,
且在点x=b附近的左侧f′(x)<0,右侧f′ (x)>0
极小值点、极大值点统称极值点,
极大值和极小值统称为极值.
思考:极大值一定大于极小值吗?
【牛刀小试!】指出哪些是极大值点, 哪些是极大值.哪些是极小值点,哪些是极小值?
极大值点:d,a,h
极小值点c,e,g
极大值:f(d),f(a),f(h)
a
极小值:f(c),f(e),f(g)
2、极值是一个局部的性质,在整定义域内可能有多个极值点
1、极大值与极小值没有必然关系,极大值可能比极小值还小.
【知识归纳:】
例1:求函数 的极值.
【例题讲解】
【方法归纳】求函数极值的一般步骤:
求导—求极点—列表—求极值
左负右正为极小值,左正右负为极大值。
(1)确定定义域并求导;
(2)令f’(x)=0并求出方程的根;
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
【课堂探究】
f?(x0) =0 x0 是可导函数f(x)的极值点
注意:f /(x0)=0是函数取得极值的必要不充分条件
导数值为0的点一定是函数的极值点吗?
【巩固练习1】观察下图并回答问题
(1)如图是函数 的图象,试找出函数
的极值点,并指出哪些是极大值点,哪些是极小值点?
(2)如果把函数图象改为导函数 的图象?
求函数 的极值
【巩固练习2】
一、极值的概念
二、用导数法求极值的步骤
(1)确定函数的定义域
(2)求导数f'(x)
(3)求方程f'(x) =0的全部解
(4)检查f'(x)在f'(x) =0的根左.右两边值的符号,如果左正右负(或左负右正),那么f(x)在这个根取得极大值或极小值
三、通过本节课使我们学会了应用数形结合法去求函数极值
课堂小结
谢 谢
同课章节目录
