8.3.1棱柱、棱锥、棱台表面积和体积 教案——2020-2021学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.3.1棱柱、棱锥、棱台表面积和体积 教案——2020-2021学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 07:21:02 | ||
图片预览

文档简介
《课时备课工具——“导评用”案》
第
八
章:
第
3
单元
第
1
课时
共
3
课时
学
科
高一数学
课
型
新授课
课
题
8.3.1棱柱、棱锥、棱台的表面积和体积
知识梳理
发展数学运算素养
表面积求法
本节知识
直观想象
体积求法
教学重点
表面积和体积求法
教学难点
解决实际问题
板书设计
8.3.1
棱柱、棱锥、棱台表面积和体积
一、棱柱表面积、体积
二、棱锥表面积、体积
三、棱台表面积、体积
学习目标
1.通过对柱体、锥体、台体的研究,掌握柱体、锥体、台体的表面积的求法.
2.了解柱体、锥体、台体的表面积计算公式.
3.能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题.
4.通过学习并运用棱柱、棱锥、棱台的表面积和体积公式,提升数学运算、直观想象、逻辑推理等素养.
核心情境
已有的长方体、正方体的基础表面积和体积概念
学习任务一:棱柱、棱锥、棱台的表面积
学习评价:熟悉公式
教学过程:
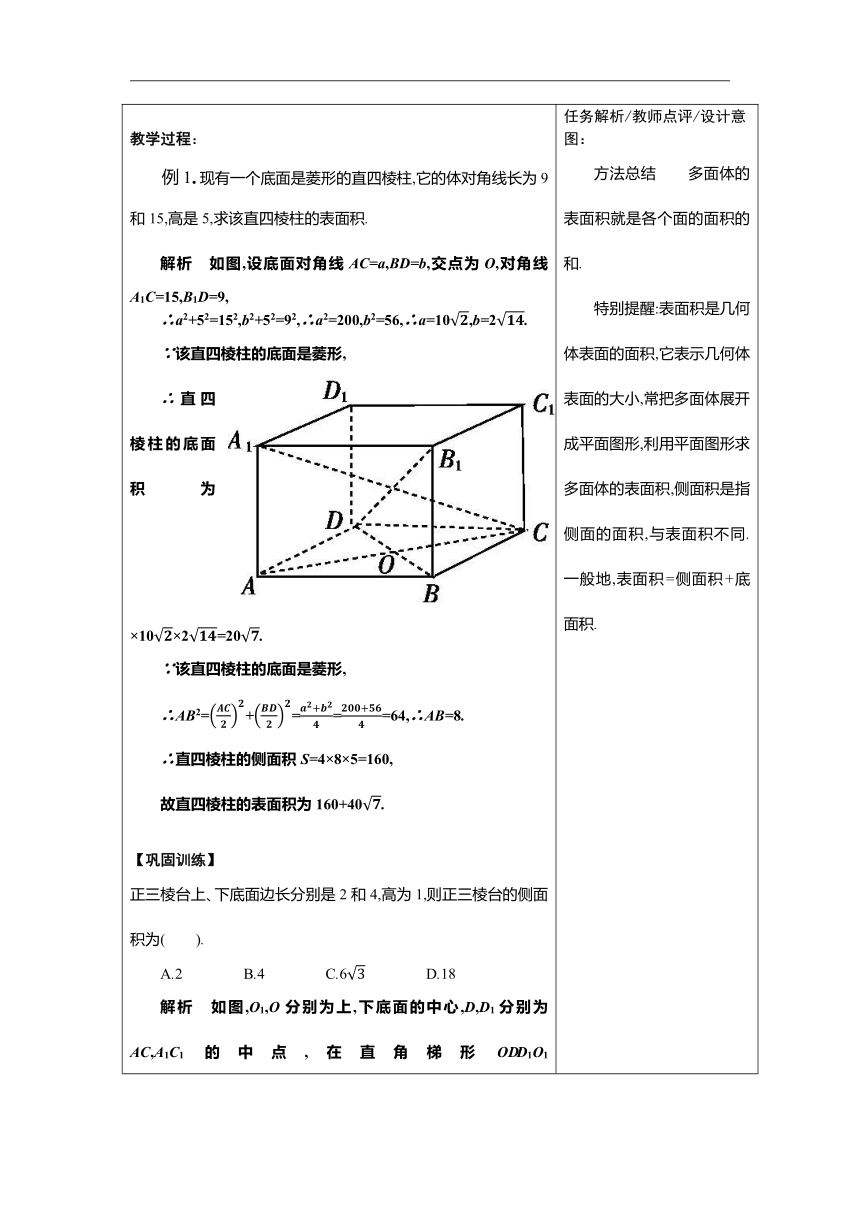
例1.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的表面积.
解析 如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,∴a2=200,b2=56,∴a=10,b=2.
∵该直四棱柱的底面是菱形,
∴直四棱柱的底面积为×10×2=20.
∵该直四棱柱的底面是菱形,
∴AB2=+===64,∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160,
故直四棱柱的表面积为160+40.
【巩固训练】
正三棱台上、下底面边长分别是2和4,高为1,则正三棱台的侧面积为( ).
A.2 B.4 C.6 D.18
解析 如图,O1,O分别为上,下底面的中心,D,D1分别为AC,A1C1的中点,在直角梯形ODD1O1中,OD=××4=,O1D1=××2=,
∴DE=OD-O1D1=.在Rt△DED1中,D1E=1,
则D1D==,
∴S棱台侧=3×(2+4)×=6.
任务解析/教师点评/设计意图:
方法总结
多面体的表面积就是各个面的面积的和.
特别提醒:表面积是几何体表面的面积,它表示几何体表面的大小,常把多面体展开成平面图形,利用平面图形求多面体的表面积,侧面积是指侧面的面积,与表面积不同.一般地,表面积=侧面积+底面积.
学习任务二:棱柱、棱锥、棱台的体积
学习评价:熟悉体积公式
教学过程:
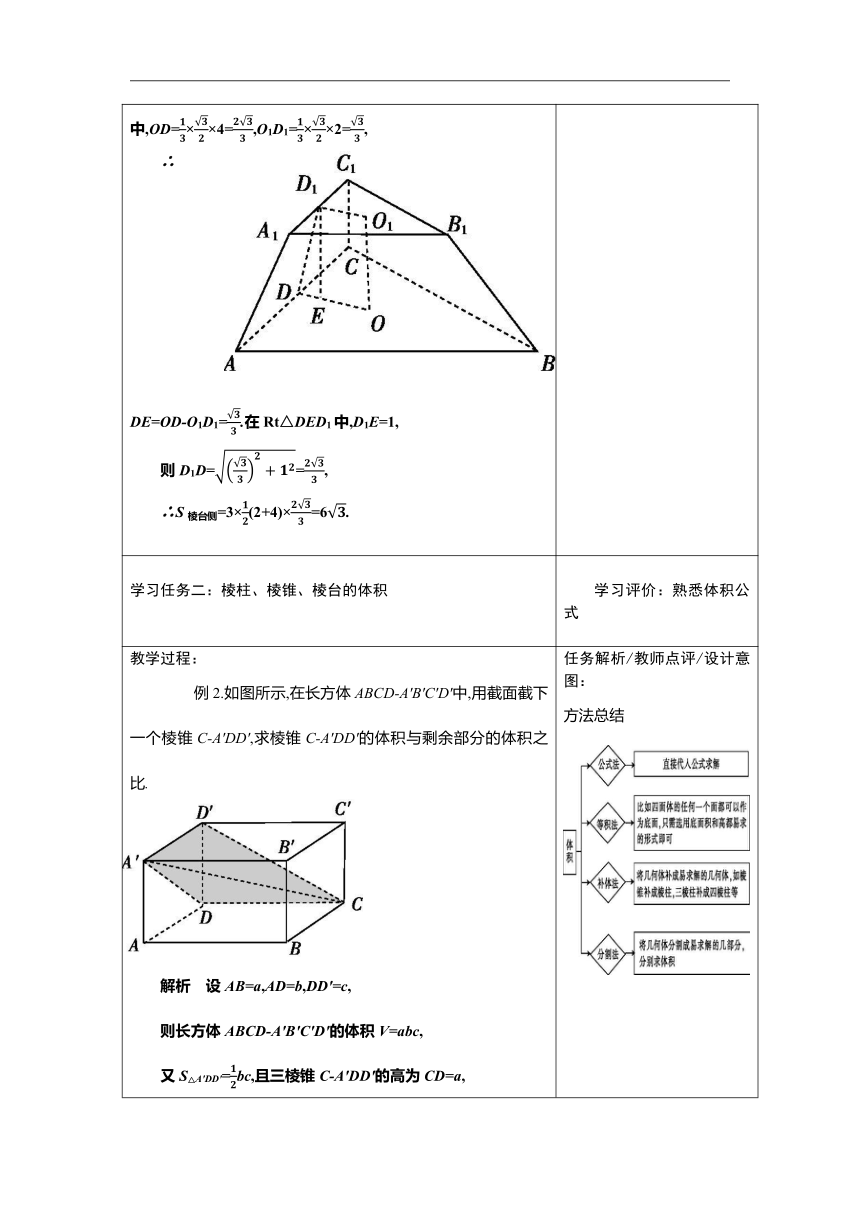
例2.如图所示,在长方体ABCD-A'B'C'D'中,用截面截下一个棱锥C-A'DD',求棱锥C-A'DD'的体积与剩余部分的体积之比.
解析 设AB=a,AD=b,DD'=c,
则长方体ABCD-A'B'C'D'的体积V=abc,
又S△A'DD'=bc,且三棱锥C-A'DD'的高为CD=a,
所以V三棱锥C-A'DD'=S△A'D'D·CD=abc.
则剩余部分的体积V剩=abc-abc=abc.
故V棱锥C-A'DD'∶V剩=abc∶abc=1∶5.
【巩固训练】
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为 .?
解析 利用三棱锥的体积公式直接求解.
==·AB=××1×1×1=.
任务解析/教师点评/设计意图:
方法总结
学习任务三:数学建模、直观想象——与多面体体积相关的实际应用问题
学习评价:解决实际问题
教学过程:
学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6
cm,AA1=4
cm.3D打印所用原料密度为0.9
g/cm3.不考虑打印损耗,制作该模型所需原料的质量
为 g.?
解析 由题知挖去的四棱锥的底面是一个菱形,对角线长分别为6
cm和4
cm,
故V挖去的四棱锥=××4×6×3=12(cm3).
又V长方体=6×6×4=144(cm3),
所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),
所以制作该模型所需原料的质量为132×0.9=118.8(g).
【巩固训练】
如图,平行四边形形状的纸片是由六个边长为3cm的正三角形构成的,将它沿虚线折起来,可以得到如图所示的粽子形状的六面体,在该六面体内挖去一个最大体积的小球,则六面体剩下部分的体积是多少?(取π=3.14,≈1.73,≈1.41,结果精确到0.01)
解析 每个三角形的面积是×(3)2,六面体体积是正四面体的2倍,所以六面体体积是2×××(3)2×=54.
由于图形的对称性,内部的小球体积要最大,则球要和六个面相切,连接球心和六面体的五个顶点(图略),把六面体分成了六个三棱锥.设球的半径为R,
所以54=6×××(3)2R,解得R=2,
所以球的体积V=R3=.
所以六面体剩下部分的体积为ΔV=54-π≈59.93(cm3).
任务解析/教师点评/设计意图:
方法总结
本题牵涉到的是3D打印新时代背景下的几何体质量,读懂题意,找出关系,明确3D打印的几何体是解题关键.
【当堂检测】
1.已知各面均为等边三角形的四面体的棱长为2,则它的表面积是( ).
A.2 B.4 C.4 D.6
解析 S表=4××22=4.故选B.
2.棱长都是1的三棱锥的侧面积为( ).
A.
B.2
C.3
D.4
解析 因为侧面是全等的正三角形,所以S=3×=.
已知一个正四棱锥的底面边长为2,高为,则该正四棱锥的表面积为 .?
解析 如图,四棱锥P-ABCD为正四棱锥,高OP=,底面边长AB=2.
过O作OG⊥BC,垂足为G,连接PG,则斜高PG==2.
故正四棱锥的表面积S=2×2+4××2×2=12.
课堂小结
本节课主要内容:
棱锥、棱柱、棱台的表面积和体积求法
课后作业
课堂反思
第
八
章:
第
3
单元
第
1
课时
共
3
课时
学
科
高一数学
课
型
新授课
课
题
8.3.1棱柱、棱锥、棱台的表面积和体积
知识梳理
发展数学运算素养
表面积求法
本节知识
直观想象
体积求法
教学重点
表面积和体积求法
教学难点
解决实际问题
板书设计
8.3.1
棱柱、棱锥、棱台表面积和体积
一、棱柱表面积、体积
二、棱锥表面积、体积
三、棱台表面积、体积
学习目标
1.通过对柱体、锥体、台体的研究,掌握柱体、锥体、台体的表面积的求法.
2.了解柱体、锥体、台体的表面积计算公式.
3.能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题.
4.通过学习并运用棱柱、棱锥、棱台的表面积和体积公式,提升数学运算、直观想象、逻辑推理等素养.
核心情境
已有的长方体、正方体的基础表面积和体积概念
学习任务一:棱柱、棱锥、棱台的表面积
学习评价:熟悉公式
教学过程:
例1.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的表面积.
解析 如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,∴a2=200,b2=56,∴a=10,b=2.
∵该直四棱柱的底面是菱形,
∴直四棱柱的底面积为×10×2=20.
∵该直四棱柱的底面是菱形,
∴AB2=+===64,∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160,
故直四棱柱的表面积为160+40.
【巩固训练】
正三棱台上、下底面边长分别是2和4,高为1,则正三棱台的侧面积为( ).
A.2 B.4 C.6 D.18
解析 如图,O1,O分别为上,下底面的中心,D,D1分别为AC,A1C1的中点,在直角梯形ODD1O1中,OD=××4=,O1D1=××2=,
∴DE=OD-O1D1=.在Rt△DED1中,D1E=1,
则D1D==,
∴S棱台侧=3×(2+4)×=6.
任务解析/教师点评/设计意图:
方法总结
多面体的表面积就是各个面的面积的和.
特别提醒:表面积是几何体表面的面积,它表示几何体表面的大小,常把多面体展开成平面图形,利用平面图形求多面体的表面积,侧面积是指侧面的面积,与表面积不同.一般地,表面积=侧面积+底面积.
学习任务二:棱柱、棱锥、棱台的体积
学习评价:熟悉体积公式
教学过程:
例2.如图所示,在长方体ABCD-A'B'C'D'中,用截面截下一个棱锥C-A'DD',求棱锥C-A'DD'的体积与剩余部分的体积之比.
解析 设AB=a,AD=b,DD'=c,
则长方体ABCD-A'B'C'D'的体积V=abc,
又S△A'DD'=bc,且三棱锥C-A'DD'的高为CD=a,
所以V三棱锥C-A'DD'=S△A'D'D·CD=abc.
则剩余部分的体积V剩=abc-abc=abc.
故V棱锥C-A'DD'∶V剩=abc∶abc=1∶5.
【巩固训练】
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为 .?
解析 利用三棱锥的体积公式直接求解.
==·AB=××1×1×1=.
任务解析/教师点评/设计意图:
方法总结
学习任务三:数学建模、直观想象——与多面体体积相关的实际应用问题
学习评价:解决实际问题
教学过程:
学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6
cm,AA1=4
cm.3D打印所用原料密度为0.9
g/cm3.不考虑打印损耗,制作该模型所需原料的质量
为 g.?
解析 由题知挖去的四棱锥的底面是一个菱形,对角线长分别为6
cm和4
cm,
故V挖去的四棱锥=××4×6×3=12(cm3).
又V长方体=6×6×4=144(cm3),
所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),
所以制作该模型所需原料的质量为132×0.9=118.8(g).
【巩固训练】
如图,平行四边形形状的纸片是由六个边长为3cm的正三角形构成的,将它沿虚线折起来,可以得到如图所示的粽子形状的六面体,在该六面体内挖去一个最大体积的小球,则六面体剩下部分的体积是多少?(取π=3.14,≈1.73,≈1.41,结果精确到0.01)
解析 每个三角形的面积是×(3)2,六面体体积是正四面体的2倍,所以六面体体积是2×××(3)2×=54.
由于图形的对称性,内部的小球体积要最大,则球要和六个面相切,连接球心和六面体的五个顶点(图略),把六面体分成了六个三棱锥.设球的半径为R,
所以54=6×××(3)2R,解得R=2,
所以球的体积V=R3=.
所以六面体剩下部分的体积为ΔV=54-π≈59.93(cm3).
任务解析/教师点评/设计意图:
方法总结
本题牵涉到的是3D打印新时代背景下的几何体质量,读懂题意,找出关系,明确3D打印的几何体是解题关键.
【当堂检测】
1.已知各面均为等边三角形的四面体的棱长为2,则它的表面积是( ).
A.2 B.4 C.4 D.6
解析 S表=4××22=4.故选B.
2.棱长都是1的三棱锥的侧面积为( ).
A.
B.2
C.3
D.4
解析 因为侧面是全等的正三角形,所以S=3×=.
已知一个正四棱锥的底面边长为2,高为,则该正四棱锥的表面积为 .?
解析 如图,四棱锥P-ABCD为正四棱锥,高OP=,底面边长AB=2.
过O作OG⊥BC,垂足为G,连接PG,则斜高PG==2.
故正四棱锥的表面积S=2×2+4××2×2=12.
课堂小结
本节课主要内容:
棱锥、棱柱、棱台的表面积和体积求法
课后作业
课堂反思
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
