人教版数学七年级上册 第3章 一元一次方程 复习教案
文档属性
| 名称 | 人教版数学七年级上册 第3章 一元一次方程 复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 23:56:11 | ||
图片预览

文档简介
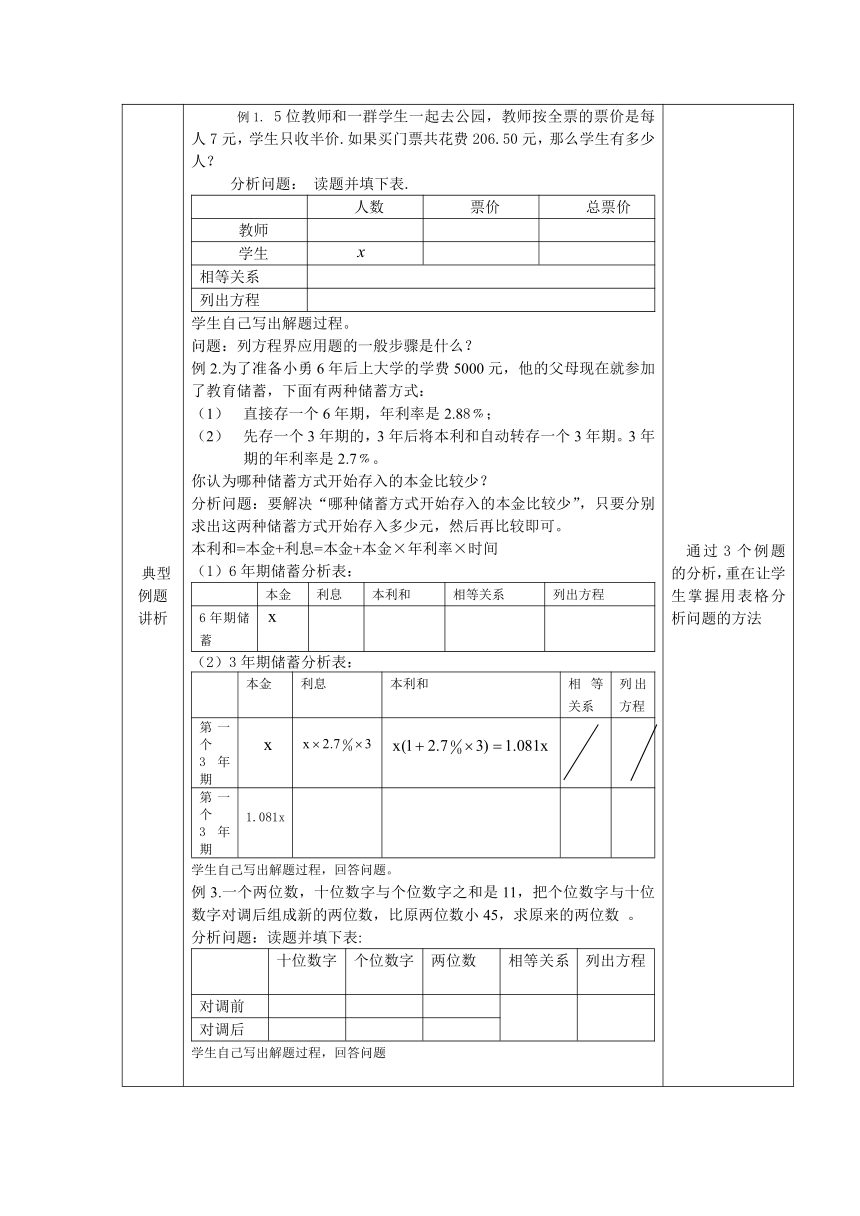
一元一次方程复习(二)
————
一元一次方程的应用
教学设计(特色班)
【课题】:
一元一次方程复习(二)——-
一元一次方程应用
【设计与执教者】:广州开发区中学
【学情分析】:学生已经复习了解一元一次方程的有关知识,并自己复习了列方程解应用题的一般步骤,而对于找相等关系列方程仍是一大难点。
【教学目标】:
1.使学生能借助图表整体把握和分析题意,恰当的转化和分析量与量之间的关系找出等量关系,进一步提高学生运用方程解决实际问题的能力;
2.通过观察、实践、讨论等活动,让学生经历从实际问题中抽象数学模型的过程,体会数学的应用价值;
3.通过学习,使学生更加关注生活,增强用数学的意识。
重点:找相等关系,学会用方程解决实际问题
难点:寻找等量关系,间接设元。.
【教学突破点】:通过表格直观、形象的分析问题,突破难点。
【教法、学法设计】:建立分析问题的思路,使学生举一反三,最后形成能力
。
【课前准备】:课本、
【教学过程设计】:
教学环节
活动设计
设计意图
知识框架图
回顾用一元一次方程解决实际问题的一般环节,用红色强调本节的难点
典型例题讲析
例1.
5位教师和一群学生一起去公园,教师按全票的票价是每人7元,学生只收半价.如果买门票共花费206.50元,那么学生有多少人?分析问题:
读题并填下表.人数票价总票价教师学生相等关系列出方程学生自己写出解题过程。问题:列方程界应用题的一般步骤是什么?例2.为了准备小勇6年后上大学的学费5000元,他的父母现在就参加了教育储蓄,下面有两种储蓄方式:直接存一个6年期,年利率是2.88﹪;先存一个3年期的,3年后将本利和自动转存一个3年期。3年期的年利率是2.7﹪。你认为哪种储蓄方式开始存入的本金比较少?分析问题:要解决“哪种储蓄方式开始存入的本金比较少”,只要分别求出这两种储蓄方式开始存入多少元,然后再比较即可。本利和=本金+利息=本金+本金×年利率×时间(1)6年期储蓄分析表:本金利息本利和相等关系列出方程
6年期储蓄(2)3年期储蓄分析表:本金利息本利和相等关系列出方程
第一个3年期第一个3年期1.081x学生自己写出解题过程,回答问题。例3.一个两位数,十位数字与个位数字之和是11,把个位数字与十位数字对调后组成新的两位数,比原两位数小45,求原来的两位数
。分析问题:读题并填下表:
十位数字个位数字两位数相等关系
列出方程对调前对调后学生自己写出解题过程,回答问题
通过3个例题的分析,重在让学生掌握用表格分析问题的方法
综合应用巩固提高
(天津市中考题)甲上午6时
步行从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发于下午3时到达B地,问乙在什么时间追上甲?
学以致用,把知识转化为能力
拓展与创新
1.你能用一元一次方程解决下面的问题吗?在3时和4时之间的那个时刻,钟的时针与分针:重合;(2)成平角;(3)成直角.(提示:分针转动的速度是时针的12倍,3:00分针与时针成直角)2.教材114页第9题.
用知识解决问题,培养学生的“转化”问题的能力
课堂小结知识梳理
谈谈本节课你的收获
锻炼学生归纳总结的能力
布置作业自我评价
1.必做题:教材第113页第4、5、6题2.选做题教材第114页第7题
巩固知识,形成能力;拓展思路,活学活用
全章复习(1)
测试与练习
班级
姓名____________
A层
1.一项工程,甲独做m天完成,乙独做比甲晚3天才能完成,甲、乙二人合作需要______天完成.
2.一个两位数,二个数位上数字之和为x,若个位上的数为2,则这个两位数为_______.
3.一件商品标价a元,打九折后,再打九折,那么现在的售价是_______.
4.下面的方程变形中:
①2x+6=-3变形为2x=-3+6;②=1变形为2x+6-3x+3=6;
③x-x=变形为6x-10x=5;④x=2(x-1)+1变形为3x=10(x-1)+1.
正确的是_________(只填代号).
5.已知等式a=b,c为任意有理数,则下列等式中,不一定成立的是(
).
A.a-c=b-c
B.a+c=b+c
C.-ac=-bc
D.
6.某数x的43%比它的一半少7,则列出求x的方程应是(
).
A.43%x-
B.43%(x-)=7
C.43%x-
D.x-7=43%x
B层
7.某校买了一批树苗,绿化校园,第一天种了全部树苗的,第二天种了50棵,两天合计种了90棵,那么剩下没有种上的树苗棵数是(
).
A.50棵
B.40棵
C.30棵
D.20棵
8.解方程:.
9.解方程:2x-(x-3)=
[x-(3x+1)].
10.某市居民生活用电基本价格为每度0.40元,若每月用电量超过a度,超过部分按基本电价的70%收费.
(1)某户5月份用电84度,共交电费30.72元,求a的值.
(2)若该户6月份的电费平均每度为0.36元,求6月份共用电多少度?应该交电费多少元?
C层
11.一人从家走到汽车站,第一小时走了3千米,他看了一下表,估计按这个速度要迟到40分钟,因此,他以每小时4千米的速度走剩下的路,结果反而提前45分到达,求此人的家到汽车站的距离.
12.一件工程,甲、乙、丙单独做各需10天、12天、15天才能完成,现在计划开工7天完成,乙、丙先合做3天后,乙队因事离去,由甲队代替,在各队工作效率都不变的情况下,能否按计划完成此工程?
全章复习(1)解答
1.
2.10(x-2)+2
3.0.81a元
4.③
5.D
6.D
7.C
8.x=-19
9.x=-
10.(1)a=60,0.40a+(84-a)×0.40×70%=30.72,a=60
(2)90度,32.40元,设该户六月份共用电x度,
则0.40×60+(x-60)×0.40×70%=0.36x,
x=90,0.36x=0.36×90=32.40(元).
11.20千米,设此人的家到汽车站的距离为x千米,则+1.
12.设甲、丙两队还需x天才能完成这工程,则=1,x=3.3,
因为3+3.3<7,所以能在计划规定的时间内完成.
合理
验证
求出
分析
实际问题
数学问题
已知量、未知量、等量关系
列方程
抽象
方程的解
解的合理性
解释
————
一元一次方程的应用
教学设计(特色班)
【课题】:
一元一次方程复习(二)——-
一元一次方程应用
【设计与执教者】:广州开发区中学
【学情分析】:学生已经复习了解一元一次方程的有关知识,并自己复习了列方程解应用题的一般步骤,而对于找相等关系列方程仍是一大难点。
【教学目标】:
1.使学生能借助图表整体把握和分析题意,恰当的转化和分析量与量之间的关系找出等量关系,进一步提高学生运用方程解决实际问题的能力;
2.通过观察、实践、讨论等活动,让学生经历从实际问题中抽象数学模型的过程,体会数学的应用价值;
3.通过学习,使学生更加关注生活,增强用数学的意识。
重点:找相等关系,学会用方程解决实际问题
难点:寻找等量关系,间接设元。.
【教学突破点】:通过表格直观、形象的分析问题,突破难点。
【教法、学法设计】:建立分析问题的思路,使学生举一反三,最后形成能力
。
【课前准备】:课本、
【教学过程设计】:
教学环节
活动设计
设计意图
知识框架图
回顾用一元一次方程解决实际问题的一般环节,用红色强调本节的难点
典型例题讲析
例1.
5位教师和一群学生一起去公园,教师按全票的票价是每人7元,学生只收半价.如果买门票共花费206.50元,那么学生有多少人?分析问题:
读题并填下表.人数票价总票价教师学生相等关系列出方程学生自己写出解题过程。问题:列方程界应用题的一般步骤是什么?例2.为了准备小勇6年后上大学的学费5000元,他的父母现在就参加了教育储蓄,下面有两种储蓄方式:直接存一个6年期,年利率是2.88﹪;先存一个3年期的,3年后将本利和自动转存一个3年期。3年期的年利率是2.7﹪。你认为哪种储蓄方式开始存入的本金比较少?分析问题:要解决“哪种储蓄方式开始存入的本金比较少”,只要分别求出这两种储蓄方式开始存入多少元,然后再比较即可。本利和=本金+利息=本金+本金×年利率×时间(1)6年期储蓄分析表:本金利息本利和相等关系列出方程
6年期储蓄(2)3年期储蓄分析表:本金利息本利和相等关系列出方程
第一个3年期第一个3年期1.081x学生自己写出解题过程,回答问题。例3.一个两位数,十位数字与个位数字之和是11,把个位数字与十位数字对调后组成新的两位数,比原两位数小45,求原来的两位数
。分析问题:读题并填下表:
十位数字个位数字两位数相等关系
列出方程对调前对调后学生自己写出解题过程,回答问题
通过3个例题的分析,重在让学生掌握用表格分析问题的方法
综合应用巩固提高
(天津市中考题)甲上午6时
步行从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发于下午3时到达B地,问乙在什么时间追上甲?
学以致用,把知识转化为能力
拓展与创新
1.你能用一元一次方程解决下面的问题吗?在3时和4时之间的那个时刻,钟的时针与分针:重合;(2)成平角;(3)成直角.(提示:分针转动的速度是时针的12倍,3:00分针与时针成直角)2.教材114页第9题.
用知识解决问题,培养学生的“转化”问题的能力
课堂小结知识梳理
谈谈本节课你的收获
锻炼学生归纳总结的能力
布置作业自我评价
1.必做题:教材第113页第4、5、6题2.选做题教材第114页第7题
巩固知识,形成能力;拓展思路,活学活用
全章复习(1)
测试与练习
班级
姓名____________
A层
1.一项工程,甲独做m天完成,乙独做比甲晚3天才能完成,甲、乙二人合作需要______天完成.
2.一个两位数,二个数位上数字之和为x,若个位上的数为2,则这个两位数为_______.
3.一件商品标价a元,打九折后,再打九折,那么现在的售价是_______.
4.下面的方程变形中:
①2x+6=-3变形为2x=-3+6;②=1变形为2x+6-3x+3=6;
③x-x=变形为6x-10x=5;④x=2(x-1)+1变形为3x=10(x-1)+1.
正确的是_________(只填代号).
5.已知等式a=b,c为任意有理数,则下列等式中,不一定成立的是(
).
A.a-c=b-c
B.a+c=b+c
C.-ac=-bc
D.
6.某数x的43%比它的一半少7,则列出求x的方程应是(
).
A.43%x-
B.43%(x-)=7
C.43%x-
D.x-7=43%x
B层
7.某校买了一批树苗,绿化校园,第一天种了全部树苗的,第二天种了50棵,两天合计种了90棵,那么剩下没有种上的树苗棵数是(
).
A.50棵
B.40棵
C.30棵
D.20棵
8.解方程:.
9.解方程:2x-(x-3)=
[x-(3x+1)].
10.某市居民生活用电基本价格为每度0.40元,若每月用电量超过a度,超过部分按基本电价的70%收费.
(1)某户5月份用电84度,共交电费30.72元,求a的值.
(2)若该户6月份的电费平均每度为0.36元,求6月份共用电多少度?应该交电费多少元?
C层
11.一人从家走到汽车站,第一小时走了3千米,他看了一下表,估计按这个速度要迟到40分钟,因此,他以每小时4千米的速度走剩下的路,结果反而提前45分到达,求此人的家到汽车站的距离.
12.一件工程,甲、乙、丙单独做各需10天、12天、15天才能完成,现在计划开工7天完成,乙、丙先合做3天后,乙队因事离去,由甲队代替,在各队工作效率都不变的情况下,能否按计划完成此工程?
全章复习(1)解答
1.
2.10(x-2)+2
3.0.81a元
4.③
5.D
6.D
7.C
8.x=-19
9.x=-
10.(1)a=60,0.40a+(84-a)×0.40×70%=30.72,a=60
(2)90度,32.40元,设该户六月份共用电x度,
则0.40×60+(x-60)×0.40×70%=0.36x,
x=90,0.36x=0.36×90=32.40(元).
11.20千米,设此人的家到汽车站的距离为x千米,则+1.
12.设甲、丙两队还需x天才能完成这工程,则=1,x=3.3,
因为3+3.3<7,所以能在计划规定的时间内完成.
合理
验证
求出
分析
实际问题
数学问题
已知量、未知量、等量关系
列方程
抽象
方程的解
解的合理性
解释
