苏科版数学九年级上册 4.3等可能条件下的概率(二) 课件1(17张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 4.3等可能条件下的概率(二) 课件1(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 882.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 06:28:29 | ||
图片预览






文档简介
(共17张PPT)
4.3
等可能条件下的概率(二)
用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩余的3支签中任意抽出1支签.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求抽出的两支签中,1支为甲签、1支为丁签的概率.
课前作业
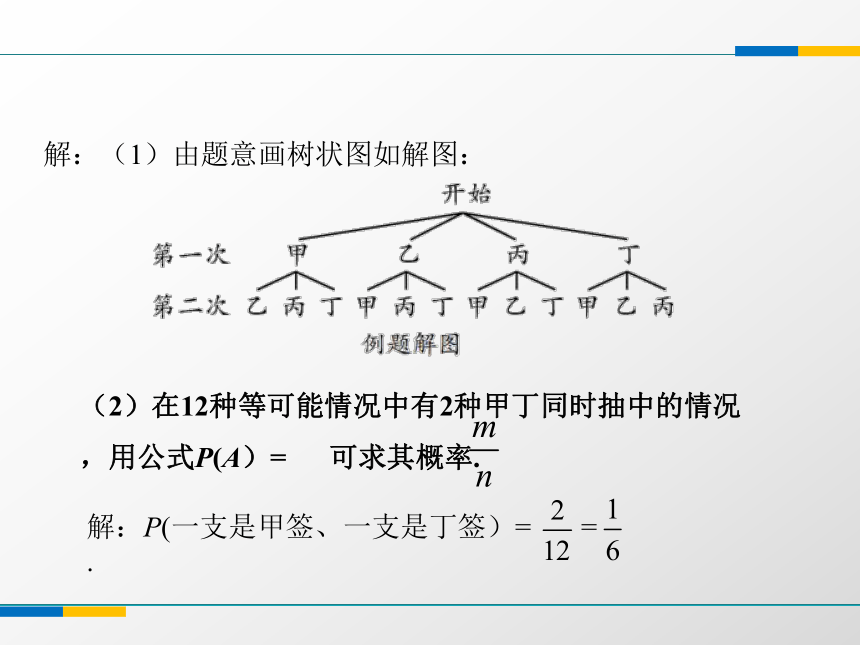
解:(1)由题意画树状图如解图:
(2)在12种等可能情况中有2种甲丁同时抽中的情况,用公式P(A)=
可求其概率.
解:P(一支是甲签、一支是丁签)=
=
.
如图是一个带指针的转盘,任意转动这个转盘,如果在某个时刻观察指针的位置.
问题1:这时所有可能结果有多少个?为什么?
问题2:每次观察有几个结果?有无第二个结果?
问题3:每个结果出现的机会是均等的吗?
情境问题
等可能条件下的概率(二)的两个特点:
1、试验结果有无限个.
2、每一个试验结果出现的等可能性.
总结:
如图是一个带指针的转盘,这个转盘被分成8个面积相等的扇形,并标上1、2、3……8,若每个扇形面积为单位1,转动转盘,转盘的指针的位置在不断的改变.
问题1:在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗?那么指针指向每一个扇形区域是等可能性吗?
问题2:怎样求指针指向每一个扇形区域的概率?它们的概率分别是多少?
问题3:在转动的过程中,当正好转了两周时呢?当正好转了n周呢?当无限周呢?
求概率的方法:
指针指向某个区域面积/整个转盘面积
概率与指针经过的区域面积大小和整个转盘区域面积大小有关.但由于转盘区域面积一定.所以只与指针的指向区域面积有关,指针指向区域越大则概率越大.
不论转多少周,指针指向每个不同号码的扇形区域的概率是相等的,且概率大小与转的周数无关,这样可把无限周问题转化为一周来解决,把无限事件转化为有限事件来处理,进而把这种类型的几何概型转化为古典概型的问题.
如图是2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
问题1:第一个转盘转一周时,试验结果有几个,其中有几个结果指向红色区域?概率是多少?
问题2:用同样的方法研究第二个转盘,则第二个转盘指向红色区域的概率是多少?
探究思考
问题3:哪一个转盘指向红色区域概率大?你认为概率大小与什么
因素有直接关系?
问题4:根据前面求概率的方法若要改变这两个转盘指针指向红色区域的概率,需要改变什么?
问题5:若把转盘变成正方形其余不变,结果是一样吗?若每个转盘中红色扇形的个数不变,但位置变化一下,结果还是一样吗?
如图是2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
概率的大小是由事件发生的区域面积大小决定的.
几何概型的概率大小与随机事件所在的区域形状、位置无关.
例
时代超市为了吸引顾客,开展有奖销售活动,设立了一个可以自由转动的转盘,转盘等分为16份,其中红色1份、蓝色2份、黄色4份、白色9份.
商场规定:顾客每购满1000元的商品,就可获得一次转动转盘的机会,转盘停止时,指针指向红、蓝、黄区域,顾客可分别获得1000元、200元、100元的礼品.
某顾客购物1400元,他获得礼品的概率是多少?他分别获得1000元、200元、100元礼品的概率是多少?
例题探究
1、这位顾客有无获得一次转动转盘的机会?为什么?
2、这个问题把几何概型转化为古典概型后在试验过程中共有多少个结果?获得礼品的结果有几次?怎样求获得礼品的概率?
3、延伸:若某顾客购满2100元的商品,求获得礼品的概率是多少?
两次同时获得1000元礼品的概率是多少?
在4m远外向地毯扔沙包,地毯中每一块小正方形除颜色外完全相同,假定沙包击中每一块小正方形是等可能的,扔沙包1次,击中红色区域的概率多大?
动手设计
设计一个转盘,使得指针指向红色区域的概率为1/2,指针指向黄色区域的概率为1/4,指针指向白色区域的概率为1/4.
若指针指向某颜色区域的概率为n/m,那么该颜色区域面积占整个转盘面积的n/m.
课后作业
2.一只不透明的袋子中装有两个完全相同的小球,上面分别标有1,2两个数字,若随机地从中摸出一个小球,记下号码后放回,再随机地摸出一个小球,则两次摸出小球的号码之积为偶数的概率是_________
1.在一只不透明的布袋中有红球、黄球各若干个,这些球除颜色外都相同,充分摇匀.
(2)若布袋中有3个红球,x个黄球.请写出一个x的值________.使得事件“从袋中一次摸出4个球,都是黄球”是不可能事件;
(3)若布袋中有3个红球,4个黄球.我们知道:“从袋中一次摸出4个球,至少有一个黄球”为必然事件.请你仿照这个表述,设计一个必然事件:_______________.
4.3
等可能条件下的概率(二)
用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩余的3支签中任意抽出1支签.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求抽出的两支签中,1支为甲签、1支为丁签的概率.
课前作业
解:(1)由题意画树状图如解图:
(2)在12种等可能情况中有2种甲丁同时抽中的情况,用公式P(A)=
可求其概率.
解:P(一支是甲签、一支是丁签)=
=
.
如图是一个带指针的转盘,任意转动这个转盘,如果在某个时刻观察指针的位置.
问题1:这时所有可能结果有多少个?为什么?
问题2:每次观察有几个结果?有无第二个结果?
问题3:每个结果出现的机会是均等的吗?
情境问题
等可能条件下的概率(二)的两个特点:
1、试验结果有无限个.
2、每一个试验结果出现的等可能性.
总结:
如图是一个带指针的转盘,这个转盘被分成8个面积相等的扇形,并标上1、2、3……8,若每个扇形面积为单位1,转动转盘,转盘的指针的位置在不断的改变.
问题1:在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗?那么指针指向每一个扇形区域是等可能性吗?
问题2:怎样求指针指向每一个扇形区域的概率?它们的概率分别是多少?
问题3:在转动的过程中,当正好转了两周时呢?当正好转了n周呢?当无限周呢?
求概率的方法:
指针指向某个区域面积/整个转盘面积
概率与指针经过的区域面积大小和整个转盘区域面积大小有关.但由于转盘区域面积一定.所以只与指针的指向区域面积有关,指针指向区域越大则概率越大.
不论转多少周,指针指向每个不同号码的扇形区域的概率是相等的,且概率大小与转的周数无关,这样可把无限周问题转化为一周来解决,把无限事件转化为有限事件来处理,进而把这种类型的几何概型转化为古典概型的问题.
如图是2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
问题1:第一个转盘转一周时,试验结果有几个,其中有几个结果指向红色区域?概率是多少?
问题2:用同样的方法研究第二个转盘,则第二个转盘指向红色区域的概率是多少?
探究思考
问题3:哪一个转盘指向红色区域概率大?你认为概率大小与什么
因素有直接关系?
问题4:根据前面求概率的方法若要改变这两个转盘指针指向红色区域的概率,需要改变什么?
问题5:若把转盘变成正方形其余不变,结果是一样吗?若每个转盘中红色扇形的个数不变,但位置变化一下,结果还是一样吗?
如图是2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
概率的大小是由事件发生的区域面积大小决定的.
几何概型的概率大小与随机事件所在的区域形状、位置无关.
例
时代超市为了吸引顾客,开展有奖销售活动,设立了一个可以自由转动的转盘,转盘等分为16份,其中红色1份、蓝色2份、黄色4份、白色9份.
商场规定:顾客每购满1000元的商品,就可获得一次转动转盘的机会,转盘停止时,指针指向红、蓝、黄区域,顾客可分别获得1000元、200元、100元的礼品.
某顾客购物1400元,他获得礼品的概率是多少?他分别获得1000元、200元、100元礼品的概率是多少?
例题探究
1、这位顾客有无获得一次转动转盘的机会?为什么?
2、这个问题把几何概型转化为古典概型后在试验过程中共有多少个结果?获得礼品的结果有几次?怎样求获得礼品的概率?
3、延伸:若某顾客购满2100元的商品,求获得礼品的概率是多少?
两次同时获得1000元礼品的概率是多少?
在4m远外向地毯扔沙包,地毯中每一块小正方形除颜色外完全相同,假定沙包击中每一块小正方形是等可能的,扔沙包1次,击中红色区域的概率多大?
动手设计
设计一个转盘,使得指针指向红色区域的概率为1/2,指针指向黄色区域的概率为1/4,指针指向白色区域的概率为1/4.
若指针指向某颜色区域的概率为n/m,那么该颜色区域面积占整个转盘面积的n/m.
课后作业
2.一只不透明的袋子中装有两个完全相同的小球,上面分别标有1,2两个数字,若随机地从中摸出一个小球,记下号码后放回,再随机地摸出一个小球,则两次摸出小球的号码之积为偶数的概率是_________
1.在一只不透明的布袋中有红球、黄球各若干个,这些球除颜色外都相同,充分摇匀.
(2)若布袋中有3个红球,x个黄球.请写出一个x的值________.使得事件“从袋中一次摸出4个球,都是黄球”是不可能事件;
(3)若布袋中有3个红球,4个黄球.我们知道:“从袋中一次摸出4个球,至少有一个黄球”为必然事件.请你仿照这个表述,设计一个必然事件:_______________.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
