《第1章三角形》同步能力达标测评(附解析)2021-2022学年鲁教版(五四制)七年级数学上册
文档属性
| 名称 | 《第1章三角形》同步能力达标测评(附解析)2021-2022学年鲁教版(五四制)七年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 15:52:40 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学上册《第1章三角形》同步能力达标测评(附答案)
一.选择题(共10小题,每小题3分,共计30分)
1.已知三角形的两边长分别为2和3,第三边长是奇数,则第三边长可以是( )
A.1 B.3 C.5 D.9
2.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠3=60° C.∠2=∠3 D.∠1=∠4
3.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1 B.2 C.2.5 D.3
4.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
5.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
6.已知一个三角形三边长为a、b、c,则|a﹣b﹣c|﹣|a+b﹣c|=( )
A.﹣2a+2c B.﹣2b+2c C.2a D.﹣2c
7.如图,已知∠ABC=∠DCB,AC与DB相交于点O.若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( )
A.∠A=∠D B.AB=CD C.∠ACB=∠DBC D.AC=BD
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
9.一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
10.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.则在下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④∠AMD=144°.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
二.填空题(共10小题,每小题3分,共计30分)
11.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有 对.
12.如图,已知∠ACB=90°,OA平分∠BAC,OB平分∠ABC,则∠AOB= °.
13.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
14.若三角形两条边的长分别是3,5,第三条边的长是整数,则第三条边的长的最大值是 .
15.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
16.如图,∠ADC=∠DCF=120°,AD=DC=2CF,若AE=24,则线段CE长为 .
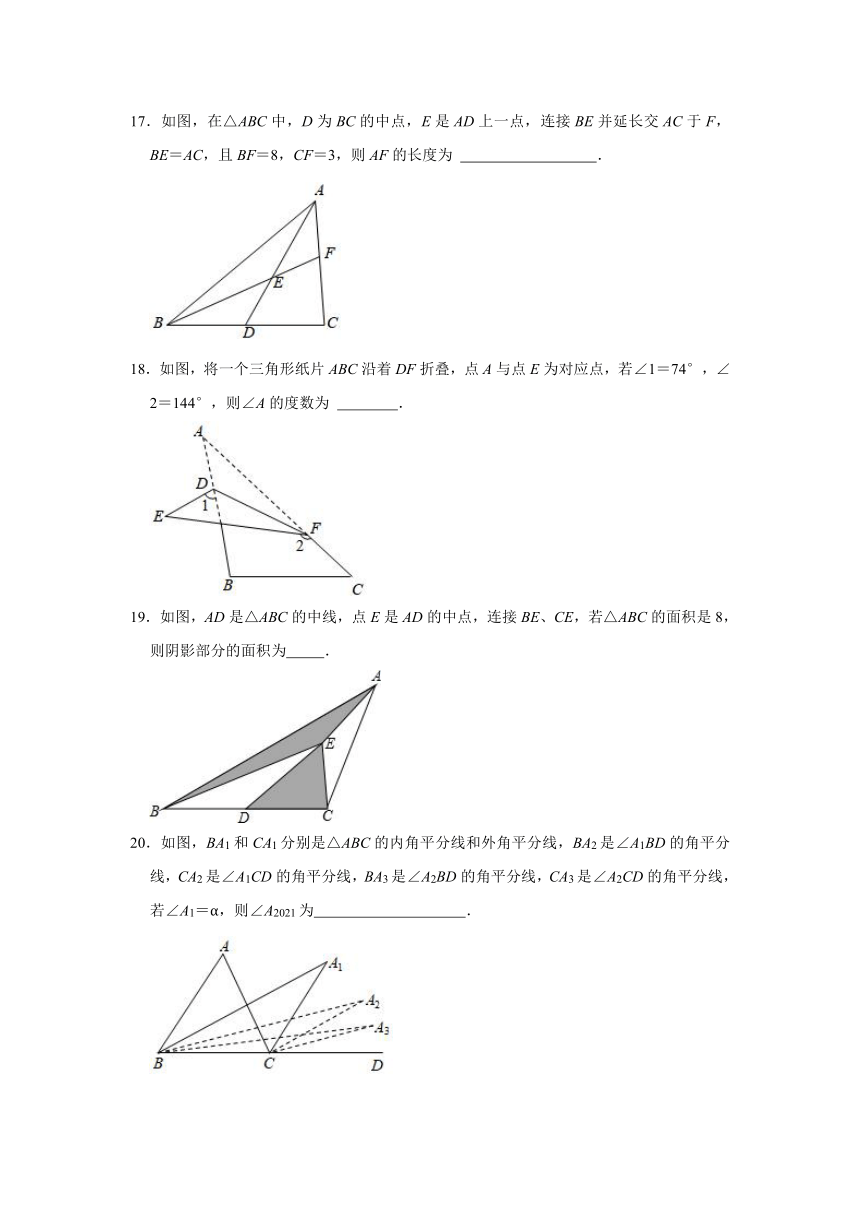
17.如图,在△ABC中,D为BC的中点,E是AD上一点,连接BE并延长交AC于F,BE=AC,且BF=8,CF=3,则AF的长度为 .
18.如图,将一个三角形纸片ABC沿着DF折叠,点A与点E为对应点,若∠1=74°,∠2=144°,则∠A的度数为 .
19.如图,AD是△ABC的中线,点E是AD的中点,连接BE、CE,若△ABC的面积是8,则阴影部分的面积为 .
20.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2021为 .
三.解答题(共6小题,每小题10分,共计60分)
21.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
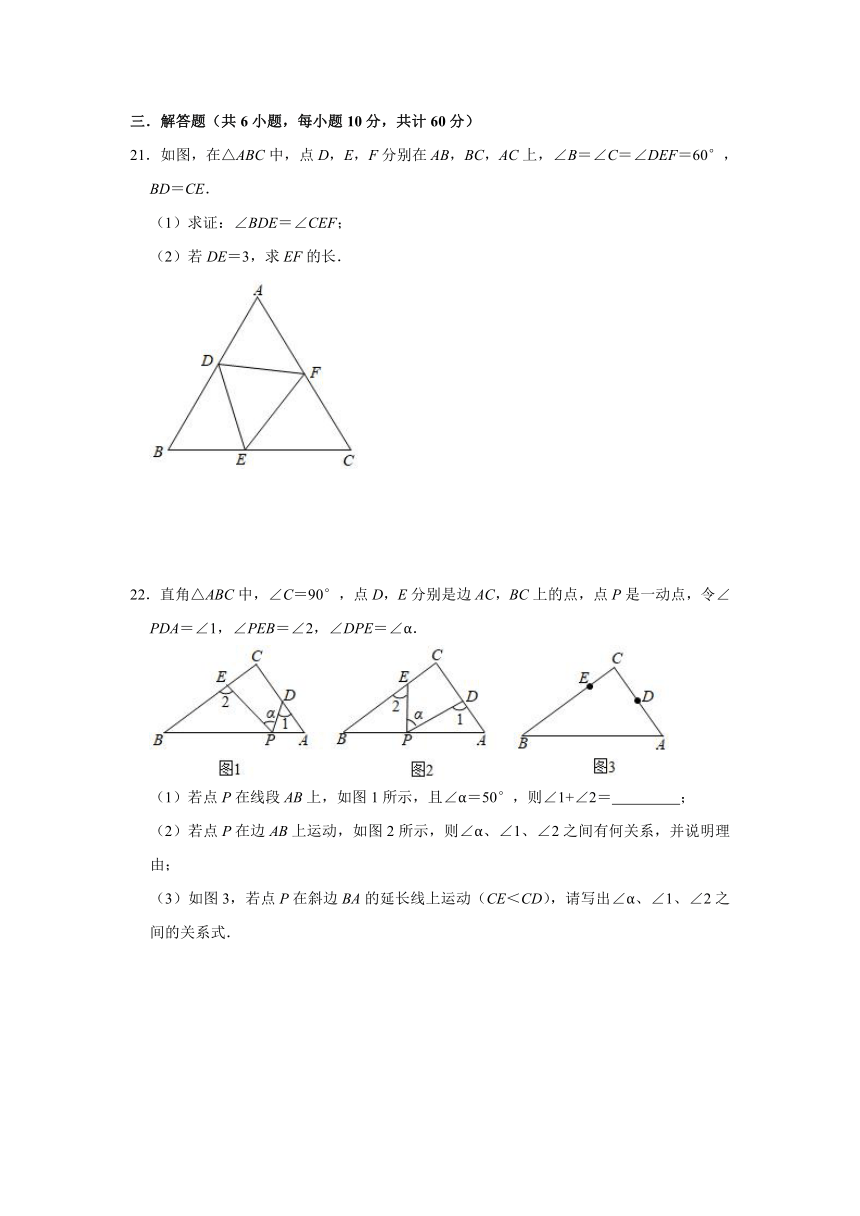
22.直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
23.如图,四边形ABCD中,点E、点F分别在AB、CD上,且AE=CF,分别过点A、C向EF作垂线,垂足分别为点G、点H,且AG=CH.求证:AB∥CD.
24.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
25.如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
26.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.
(1)求证:BD=CD.
(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.
(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:设第三边的长为x,根据三角形的三边关系,
得3﹣2<x<3+2,即1<x<5,
又∵第三边长是奇数,
∴x=3.
故选:B.
2.解:Rt△ABC中,
∵∠ACB=90°,
∴∠1+∠2=90°,故A正确;
∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,故C正确;
∵∠3+∠4=90°,
∴∠1=∠4,故D正确;
故选:B.
3.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
4.解:如图,
∵∠2=90°﹣30°=60°,
∴∠3=180°﹣45°﹣60°=75°,
∵a∥b,
∴∠1=∠3=75°,
故选:B.
5.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
6.解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a﹣b﹣c|﹣|a+b﹣c|
=﹣(a﹣b﹣c)﹣(a+b﹣c)
=﹣a+b+c﹣a﹣b+c
=﹣2a+2c,
故选:A.
7.解:A、∵∠A=∠D,∠ABC=∠DCB,BC=CB,利用AAS能判定△ABC≌△DCB,不符合题意;
B、∵AB=CD,∠ABC=∠DCB,BC=CB,利用SAS能判定△ABC≌△DCB,不符合题意;
C、∵∠ACB=∠DBC,∠ABC=∠DCB,BC=CB,利用AAS能判定△ABC≌△DCB,不符合题意;
D、∵∠ABC=∠DCB,BC=CB,AC=BD,有两边且其中一边的对角对应相等的两个三角形不一定全等,符合题意;
故选:D.
8.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)==2×55°=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
9.解:如图,∠5=90°﹣30°=60°,∠3=∠1﹣45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,
故选:B.
10.解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠BOC+∠COD,
即∠AOC=∠BOD,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠OAC=∠OBD,AC=BD,所以②正确;
∵∠AOB+∠OAC+∠1=∠AMB+∠OBD+∠2,
而∠1=∠2,
∴∠AMB=∠AOB=36°,所以①正确;
∴∠AMD=180°﹣∠AMB=180°﹣36°=144°,所以④正确;
过O点作OE⊥AC于E,OF⊥BD于F,如图,
∵△OAC≌△OBD,
∴OE=OF,
∴MO平分∠AMD,
而∠OAM≠ODM,
∴∠AOM≠∠DOM,所以③错误.
故选:B.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
12.解:∵OA平分∠BAC,OB平分∠ABC,
∴∠OAB=CAB,∠OBA=∠CBA.
∵∠AOB=180°﹣∠OAB﹣∠OBA
=180°﹣∠CAB﹣∠CBA
=180°﹣(∠CAB+∠CBA)
=180°﹣(180°﹣∠C)
=90°+∠C.
当∠ACB=90°时,
∠AOB=90°+×90°
=135°.
故答案为:135.
13.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
14.解:∵5﹣3<第三边<3+5,
即:2<第三边<8;
所以最大整数是7,
故答案为:7.
15.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
16.解:如图,过点D作DH⊥AC于H,
∵∠ADC=∠DCF=120°,AD=DC,DH⊥AC,
∴AH=HC,∠DAC=∠DCA=30°,
∴∠ACF=90°,AD=2DH,
∵AD=2CF,
∴DH=CF,
在△DHE和△FCE中,
,
∴△DHE≌△FCE(AAS)
∴EH=EC,
∴EC=EH=CH=AH,
∵AE=24,
∴EH=EC=8.
故答案为8.
17.解:如图,延长AD到G使DG=AD,连接BG,
∵D为BC的中点,
∴BD=CD,
在△ACD与△GBD中,
,
∴△ACD≌△GBD(SAS),
∴∠CAD=∠G,AC=BG,
∵BE=AC,
∴BE=BG,
∴∠G=∠BEG,
∵∠BEG=∠AEF,
∴∠AEF=∠EAF.
∴EF=AF,
∴AF+CF=BF﹣AF,
即AF+3=8﹣AF,
∴AF=,
故答案为.
18.解:延长DF
由折叠得,△ADF≌△EDF,
∴∠AFD=∠EFD,∠A=∠E,
∴∠AFE=150°﹣∠2=36°,
∴AFD=∠EFD=18°,
∵∠CFG和∠DFE为对顶角,
∵∠FDB是△ADF的外角,
∴∠E+∠EDF=∠EFG,
∴∠A+∠1+∠FDB=∠2+∠CFG,
∴∠A+∠1+∠A+∠AFD=∠2+∠CFG,
∴2∠2+74°+18°=144°+18°,
∴∠A=35°.
故答案为:35°.
19.解:∵AD是△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵点E是AD的中点,
∴S△ABE=S△ADE=S△ABD,
S△EDC=S△CAE=S△ACD,
∴S△ABE=S△ABC,S△CDE=S△ABC,
∴S△ABE+S△CDE=S△ABC+S△ABC=S△ABC==4,
故答案为:4.
20.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A1=.
故答案为:.
三.解答题(共6小题,每小题10分,共计60分)
21.(1)证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
(2)解:在△BDE和△CEF中,
,
∴△BDE≌△CEF( ASA),
∴DE=EF,
∵DE=3,
∴EF=3.
22.解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:在BA延长线上取点P,连接EP、DP,
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
23.证明:∵AG⊥GH,CH⊥GH,
∴∠G=∠H=90°,
在Rt△AGE和Rt△CHF中,
,
∴Rt△AGE≌Rt△CHF(HL),
∴∠AEG=∠CFH,
∵∠AEG=∠BEF,
∴∠BEF=∠CFH,
∴AB∥CD.
24.(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
25.(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
26.(1)证明:∵∠A=120°,∠C=20°,
∴∠ABC=180°﹣120°﹣20°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=ABC=20°,
∴∠DBC=∠C=20°,
∴BD=CD;
(2)证明:如图2,过点E作EF∥BD交AC于点F,
∴∠FEC=∠DBC=20°,
∴∠FEC=∠C=20°,
∴∠AFE=40°,FE=FC,
∴∠AFE=∠ABC,
∵AE是∠BAC的平分线,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∴BE=EF=FC,
∴AB+BE=AF+FC=AC;
(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:
如图3,过点A作AF∥BD交BE于点F,
∴∠AFC=∠DBC=20°,
∴∠AFC=∠C=20°,
∴AF=AC,
∵AE是∠BAC的外角平分线,
∴∠EAB=(180°﹣∠ABC)=30°,
∵∠ABC=40°,
∴∠E=∠ABC﹣∠EAB=10°,
∴∠E=∠FAE=10°,
∴FE=AF,
∴FE=AF=AC,
∴BE﹣AB=BE﹣BF=EF=AC.
一.选择题(共10小题,每小题3分,共计30分)
1.已知三角形的两边长分别为2和3,第三边长是奇数,则第三边长可以是( )
A.1 B.3 C.5 D.9
2.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠3=60° C.∠2=∠3 D.∠1=∠4
3.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1 B.2 C.2.5 D.3
4.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
5.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
6.已知一个三角形三边长为a、b、c,则|a﹣b﹣c|﹣|a+b﹣c|=( )
A.﹣2a+2c B.﹣2b+2c C.2a D.﹣2c
7.如图,已知∠ABC=∠DCB,AC与DB相交于点O.若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( )
A.∠A=∠D B.AB=CD C.∠ACB=∠DBC D.AC=BD
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
9.一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
10.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.则在下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④∠AMD=144°.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
二.填空题(共10小题,每小题3分,共计30分)
11.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有 对.
12.如图,已知∠ACB=90°,OA平分∠BAC,OB平分∠ABC,则∠AOB= °.
13.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
14.若三角形两条边的长分别是3,5,第三条边的长是整数,则第三条边的长的最大值是 .
15.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
16.如图,∠ADC=∠DCF=120°,AD=DC=2CF,若AE=24,则线段CE长为 .
17.如图,在△ABC中,D为BC的中点,E是AD上一点,连接BE并延长交AC于F,BE=AC,且BF=8,CF=3,则AF的长度为 .
18.如图,将一个三角形纸片ABC沿着DF折叠,点A与点E为对应点,若∠1=74°,∠2=144°,则∠A的度数为 .
19.如图,AD是△ABC的中线,点E是AD的中点,连接BE、CE,若△ABC的面积是8,则阴影部分的面积为 .
20.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2021为 .
三.解答题(共6小题,每小题10分,共计60分)
21.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
22.直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
23.如图,四边形ABCD中,点E、点F分别在AB、CD上,且AE=CF,分别过点A、C向EF作垂线,垂足分别为点G、点H,且AG=CH.求证:AB∥CD.
24.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
25.如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
26.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.
(1)求证:BD=CD.
(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.
(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:设第三边的长为x,根据三角形的三边关系,
得3﹣2<x<3+2,即1<x<5,
又∵第三边长是奇数,
∴x=3.
故选:B.
2.解:Rt△ABC中,
∵∠ACB=90°,
∴∠1+∠2=90°,故A正确;
∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,故C正确;
∵∠3+∠4=90°,
∴∠1=∠4,故D正确;
故选:B.
3.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
4.解:如图,
∵∠2=90°﹣30°=60°,
∴∠3=180°﹣45°﹣60°=75°,
∵a∥b,
∴∠1=∠3=75°,
故选:B.
5.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
6.解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a﹣b﹣c|﹣|a+b﹣c|
=﹣(a﹣b﹣c)﹣(a+b﹣c)
=﹣a+b+c﹣a﹣b+c
=﹣2a+2c,
故选:A.
7.解:A、∵∠A=∠D,∠ABC=∠DCB,BC=CB,利用AAS能判定△ABC≌△DCB,不符合题意;
B、∵AB=CD,∠ABC=∠DCB,BC=CB,利用SAS能判定△ABC≌△DCB,不符合题意;
C、∵∠ACB=∠DBC,∠ABC=∠DCB,BC=CB,利用AAS能判定△ABC≌△DCB,不符合题意;
D、∵∠ABC=∠DCB,BC=CB,AC=BD,有两边且其中一边的对角对应相等的两个三角形不一定全等,符合题意;
故选:D.
8.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)==2×55°=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
9.解:如图,∠5=90°﹣30°=60°,∠3=∠1﹣45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,
故选:B.
10.解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠BOC+∠COD,
即∠AOC=∠BOD,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠OAC=∠OBD,AC=BD,所以②正确;
∵∠AOB+∠OAC+∠1=∠AMB+∠OBD+∠2,
而∠1=∠2,
∴∠AMB=∠AOB=36°,所以①正确;
∴∠AMD=180°﹣∠AMB=180°﹣36°=144°,所以④正确;
过O点作OE⊥AC于E,OF⊥BD于F,如图,
∵△OAC≌△OBD,
∴OE=OF,
∴MO平分∠AMD,
而∠OAM≠ODM,
∴∠AOM≠∠DOM,所以③错误.
故选:B.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
12.解:∵OA平分∠BAC,OB平分∠ABC,
∴∠OAB=CAB,∠OBA=∠CBA.
∵∠AOB=180°﹣∠OAB﹣∠OBA
=180°﹣∠CAB﹣∠CBA
=180°﹣(∠CAB+∠CBA)
=180°﹣(180°﹣∠C)
=90°+∠C.
当∠ACB=90°时,
∠AOB=90°+×90°
=135°.
故答案为:135.
13.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
14.解:∵5﹣3<第三边<3+5,
即:2<第三边<8;
所以最大整数是7,
故答案为:7.
15.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
16.解:如图,过点D作DH⊥AC于H,
∵∠ADC=∠DCF=120°,AD=DC,DH⊥AC,
∴AH=HC,∠DAC=∠DCA=30°,
∴∠ACF=90°,AD=2DH,
∵AD=2CF,
∴DH=CF,
在△DHE和△FCE中,
,
∴△DHE≌△FCE(AAS)
∴EH=EC,
∴EC=EH=CH=AH,
∵AE=24,
∴EH=EC=8.
故答案为8.
17.解:如图,延长AD到G使DG=AD,连接BG,
∵D为BC的中点,
∴BD=CD,
在△ACD与△GBD中,
,
∴△ACD≌△GBD(SAS),
∴∠CAD=∠G,AC=BG,
∵BE=AC,
∴BE=BG,
∴∠G=∠BEG,
∵∠BEG=∠AEF,
∴∠AEF=∠EAF.
∴EF=AF,
∴AF+CF=BF﹣AF,
即AF+3=8﹣AF,
∴AF=,
故答案为.
18.解:延长DF
由折叠得,△ADF≌△EDF,
∴∠AFD=∠EFD,∠A=∠E,
∴∠AFE=150°﹣∠2=36°,
∴AFD=∠EFD=18°,
∵∠CFG和∠DFE为对顶角,
∵∠FDB是△ADF的外角,
∴∠E+∠EDF=∠EFG,
∴∠A+∠1+∠FDB=∠2+∠CFG,
∴∠A+∠1+∠A+∠AFD=∠2+∠CFG,
∴2∠2+74°+18°=144°+18°,
∴∠A=35°.
故答案为:35°.
19.解:∵AD是△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵点E是AD的中点,
∴S△ABE=S△ADE=S△ABD,
S△EDC=S△CAE=S△ACD,
∴S△ABE=S△ABC,S△CDE=S△ABC,
∴S△ABE+S△CDE=S△ABC+S△ABC=S△ABC==4,
故答案为:4.
20.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A1=.
故答案为:.
三.解答题(共6小题,每小题10分,共计60分)
21.(1)证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
(2)解:在△BDE和△CEF中,
,
∴△BDE≌△CEF( ASA),
∴DE=EF,
∵DE=3,
∴EF=3.
22.解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:在BA延长线上取点P,连接EP、DP,
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
23.证明:∵AG⊥GH,CH⊥GH,
∴∠G=∠H=90°,
在Rt△AGE和Rt△CHF中,
,
∴Rt△AGE≌Rt△CHF(HL),
∴∠AEG=∠CFH,
∵∠AEG=∠BEF,
∴∠BEF=∠CFH,
∴AB∥CD.
24.(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
25.(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
26.(1)证明:∵∠A=120°,∠C=20°,
∴∠ABC=180°﹣120°﹣20°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=ABC=20°,
∴∠DBC=∠C=20°,
∴BD=CD;
(2)证明:如图2,过点E作EF∥BD交AC于点F,
∴∠FEC=∠DBC=20°,
∴∠FEC=∠C=20°,
∴∠AFE=40°,FE=FC,
∴∠AFE=∠ABC,
∵AE是∠BAC的平分线,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∴BE=EF=FC,
∴AB+BE=AF+FC=AC;
(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:
如图3,过点A作AF∥BD交BE于点F,
∴∠AFC=∠DBC=20°,
∴∠AFC=∠C=20°,
∴AF=AC,
∵AE是∠BAC的外角平分线,
∴∠EAB=(180°﹣∠ABC)=30°,
∵∠ABC=40°,
∴∠E=∠ABC﹣∠EAB=10°,
∴∠E=∠FAE=10°,
∴FE=AF,
∴FE=AF=AC,
∴BE﹣AB=BE﹣BF=EF=AC.
