《12.2全等三角形的判定》同步能力达标训练 2021-2022学年人教版八年级数学上册(Word版 含解析)
文档属性
| 名称 | 《12.2全等三角形的判定》同步能力达标训练 2021-2022学年人教版八年级数学上册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学上册《12.2全等三角形的判定》
同步能力达标训练(附答案)
一.选择题(共7小题)
1.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
2.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20° B.40° C.60° D.70°
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
4.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B′C′ B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
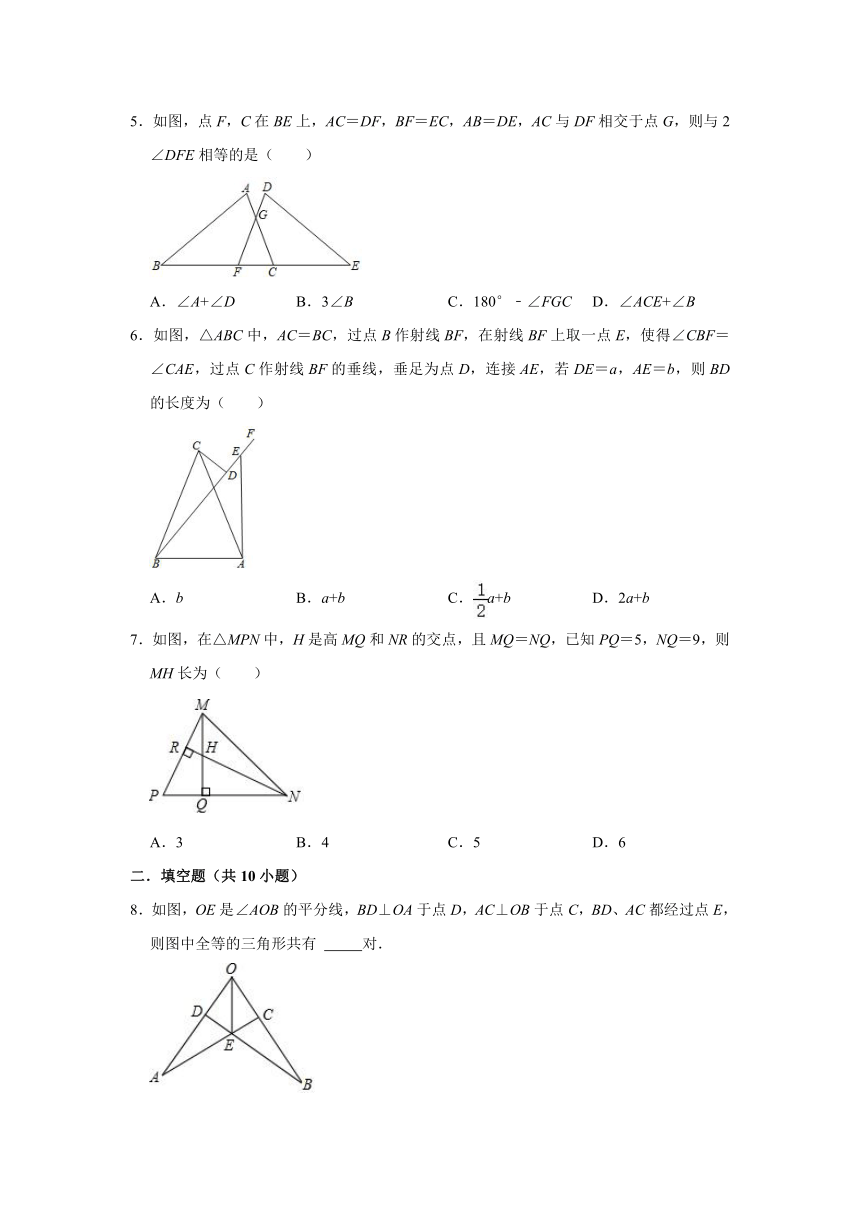
5.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是( )
A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B
6.如图,△ABC中,AC=BC,过点B作射线BF,在射线BF上取一点E,使得∠CBF=∠CAE,过点C作射线BF的垂线,垂足为点D,连接AE,若DE=a,AE=b,则BD的长度为( )
A.b B.a+b C.a+b D.2a+b
7.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH长为( )
A.3 B.4 C.5 D.6
二.填空题(共10小题)
8.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有 对.
9.如图,在△ABC中,∠ABC=2∠C,BQ和AP分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为 .
10.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是 秒.
11.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
12.一个三角形的两边长分别为2和4,则第三边上面的中线a的范围是 .
13.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
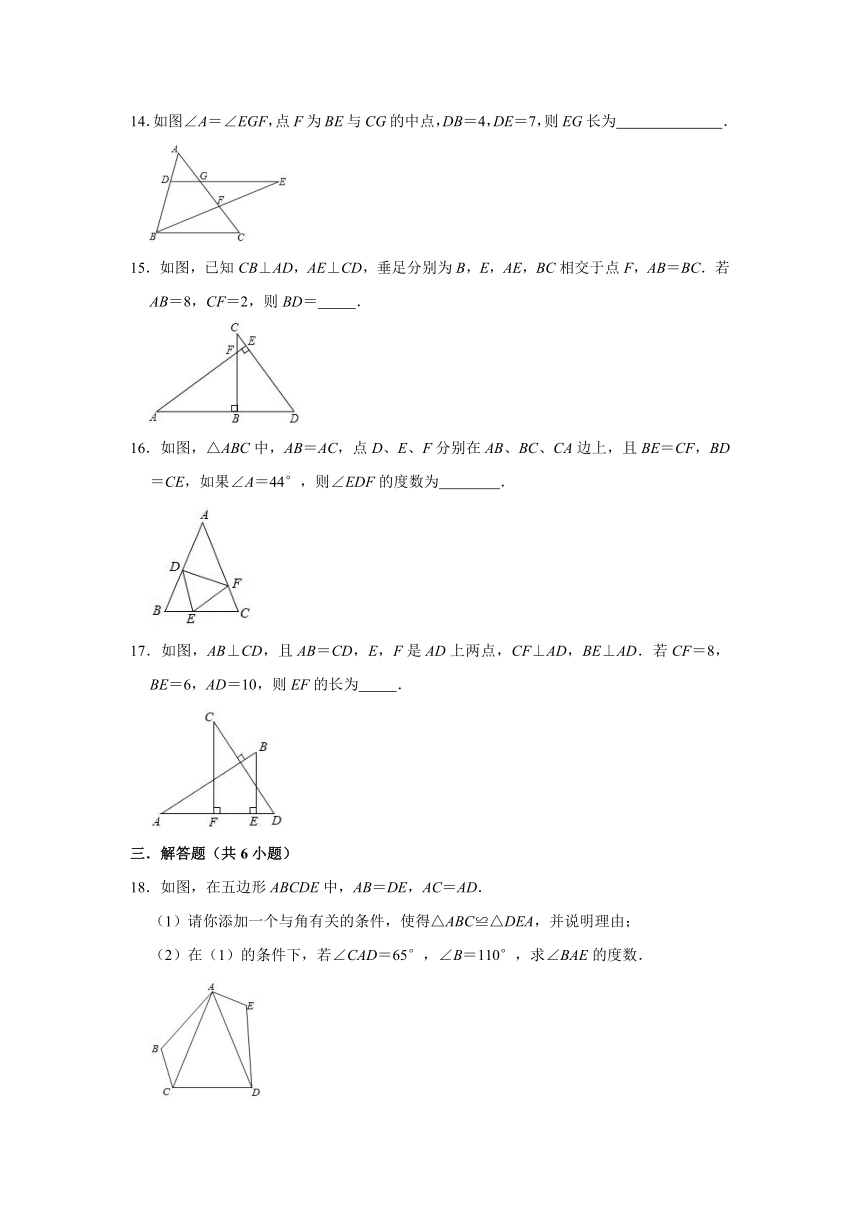
14.如图∠A=∠EGF,点F为BE与CG的中点,DB=4,DE=7,则EG长为 .
15.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD= .
16.如图,△ABC中,AB=AC,点D、E、F分别在AB、BC、CA边上,且BE=CF,BD=CE,如果∠A=44°,则∠EDF的度数为 .
17.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CF⊥AD,BE⊥AD.若CF=8,BE=6,AD=10,则EF的长为 .
三.解答题(共6小题)
18.如图,在五边形ABCDE中,AB=DE,AC=AD.
(1)请你添加一个与角有关的条件,使得△ABC≌△DEA,并说明理由;
(2)在(1)的条件下,若∠CAD=65°,∠B=110°,求∠BAE的度数.
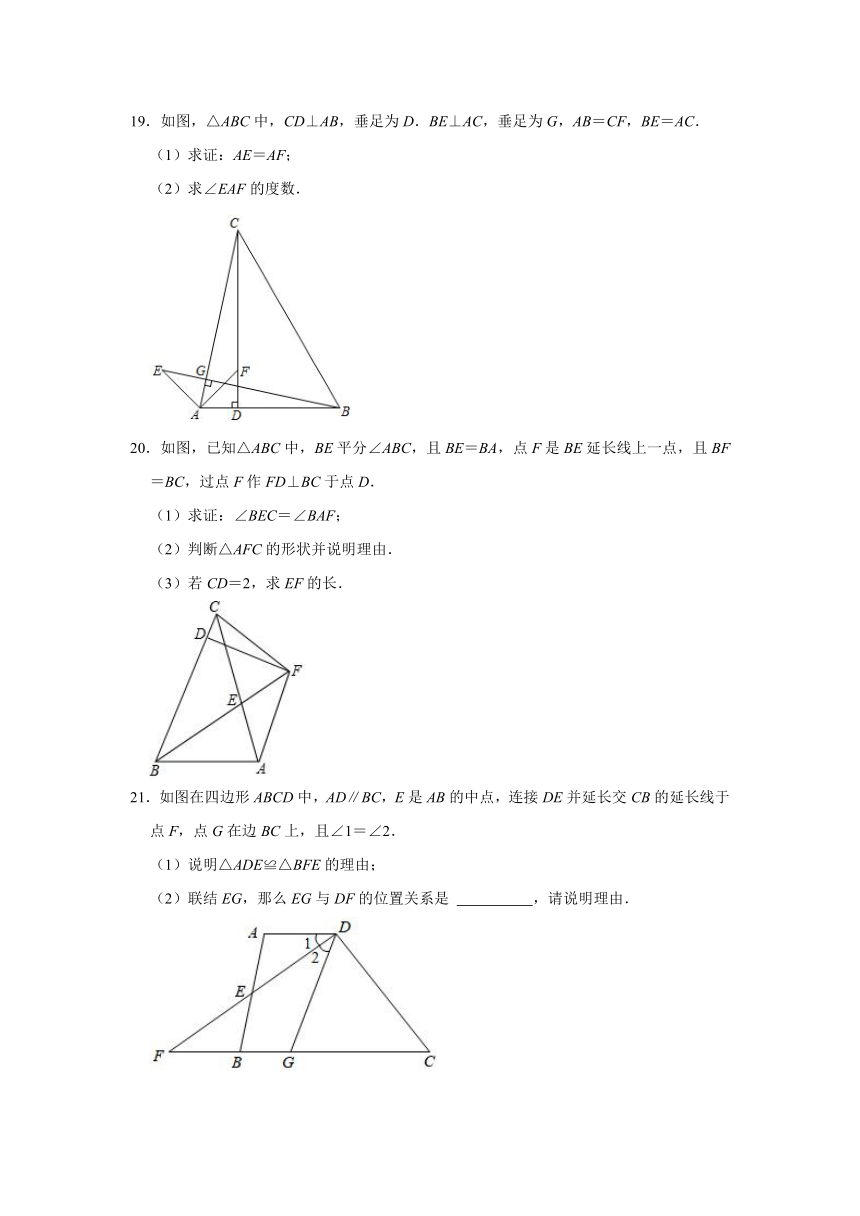
19.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
20.如图,已知△ABC中,BE平分∠ABC,且BE=BA,点F是BE延长线上一点,且BF=BC,过点F作FD⊥BC于点D.
(1)求证:∠BEC=∠BAF;
(2)判断△AFC的形状并说明理由.
(3)若CD=2,求EF的长.
21.如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 ,请说明理由.
22.已知:DF∥BC,∠FDC=∠AEC.
(1)如图1,已知CD⊥AB,CB平分∠NCE.求∠ABC的度数;
(2)如图2,若∠ABC=∠ACF,AC=FC,DM=BE.求证:BC=MC.
23.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
参考答案
一.选择题(共7小题)
1.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
2.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
3.解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
4.解:A、由AB=A′B′,AC=A′C′,BC=B′C′可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故选:C.
5.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴2∠DFE=180°﹣∠FGC,
故选:C.
6.解:如图,连接CE,过点C作CM⊥AE交AE于M.
∵CD⊥BF,CM⊥AM,
∴∠CDB=∠M=90°,
在△CDB△CMA中,
,
∴△CDB≌△CMA(AAS),
∴CM=CD,BD=AM,
在Rt△CED和Rt△CEM,
,
∴Rt△CED≌Rt△CEM(HL),
∴DE=EM=a,
∴BD=AM=AE+EM=AE+DE=a+b,
故选:B.
7.解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
故选:B.
二.填空题(共10小题)
8.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
9.解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC①,
过点P作PD∥BQ交CQ于点D,如图,
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
∵AP=AP,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC②,
由①②得BQ+AQ=AB+BP,
∵△ABQ的周长为18,BP=4,
∴AB+BQ+AQ=AB+BP+AB=2AB+4=18,
∴AB=7.
10.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
11.解:①在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.
∴①正确;
没有条件可以证明CD=DN,
∴②错误;
∵△ABE≌△ACF,
∴AB=AC,
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),
∴③正确;
∵△ABE≌△ACF,
∴BE=CF,
∴④正确.
∴其中正确的结论有①③④.
故答案为:①③④.
12.解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵三角形两边长为2,4,第三边上的中线为a,
∴4﹣2<2a<4+2,即2<2a<6,
∴1<a<3.
故答案为:1<a<3.
13.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
14.解:∵∠A=∠EGF,∠AGD=∠EGF,
∴∠A=∠AGD,
∴AD=DG,
设AD=x,则DG=x,
在△EGF和△BCF中,
∵,
∴△EGF≌△BCF(SAS),
∴BC=EG,∠E=∠EBC,
∴EG∥BC,
∴∠AGD=∠C=∠A,
∴BC=AB=x+4=EG,
∵DE=7,
∴x+x+4=7,
x=,
∴EG=x+4=,
故答案为:.
15.证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
16.解:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=(180°﹣44°)=68°
∴∠1+∠2=180°﹣68°
∴∠3+∠2=180°﹣68°
∴∠DEF=68°,
∴∠EDF=.
故答案为:56°.
17.解:∵AB⊥CD,CF⊥AD,BE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,∠AEB=∠CFD=90°,
∴∠A=∠C,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF=6,AE=CF=8,
∵AF=AD﹣DF=10﹣6=4,
∴EF=AE﹣AF=8﹣4=4,
故答案为:4.
三.解答题(共6小题)
18.解:(1)添加一个角方面的条件为:∠BAC=∠EDA,使得△ABC≌△DEA,理由如下:
在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
(2)在(1)的条件下,
∵△ABC≌△DEA,
∴∠ACB=∠DAE,
∵∠CAD=65°,∠B=110°,
∴∠ACB+∠BAC=180°﹣∠B=70°,
∴∠DAE+∠BAC=∠ACB+∠BAC=70°,
∴∠BAE=∠DAE+∠BAC+∠CAD=70°+65°=135°.
19.(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
20.解:(1)∵BE平分∠ABC,
∴∠EBC=∠ABF,
在△BEC和△BAF中,
,
∴△BEC≌△BAF(SAS),
∴∠BEC=∠BAF;
(2)△AFC是等腰三角形.
证明:过F作FG⊥BA,与BA的延长线交于点G,如图,
∵BA=BE,BC=BF,∠ABF=∠CBF,
∴∠AEB=∠BCF,
∵∠BEC=∠BAF,
∴∠GAF=∠AEB=∠BCF,
∵BF平分∠ABC,FD⊥BC,FG⊥BA,
∴FD=FG,
在△CDF和△AGF中,
,
∴△CDF≌△AGF(AAS),
∴FC=FA,
∵△ACF是等腰三角形;
(3)设AB=BE=x,
∵△CDF≌△AGF,CD=2,
∴CD=AG=2,
∴BG=BA+AG=x+2,
在Rt△BFD和Rt△BFG中,
,
∴△BFD≌△BFG(HL),
∴BD=BG=x+2,
∴BF=BC=BD+CD=x+4,
∴EF=BF﹣BE=x+4﹣x=4.
21.解:(1)∵AD∥BC,
∴∠1=∠F,
∵E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
(2)如图,EG⊥DF,
∵∠1=∠F,∠1=∠2,
∴∠2=∠F,
∴DG=FG,
由(1)知:△ADE≌△BFE,
∴DE=EF,
∴EG⊥DF.
22.解:(1)∵DF∥BC,
∴∠FDC=∠NCB,
∵CB平分∠NCE,
∴∠NCB=∠BCE,
∵∠FDC=∠AEC,
∴∠FDC=∠NCB=∠BCE=∠AEC,
∵CD⊥AB,
∴∠ENC=90°,
∴∠AEC+∠NCE=∠AEC+∠BCE+∠NCB=3∠NCB=90°,
∴∠NCB=30°,
∴∠ABC=90°﹣∠NCB=60°;
(2)∵DF∥BC,
∴∠FMC=∠ACB,
∵∠ABC=∠ACF,
∴180°﹣∠FMC﹣∠ACF=180°﹣∠ACB﹣∠ABC,
即∠F=∠BAC,
在△DFC和△EAC中,
,
∴△DFC≌△EAC(AAS),
∴CD=CE,
在△MDC和△BEC中,
,
∴△MDC≌△BEC(SAS),
∴MC=BC.
23.解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
同步能力达标训练(附答案)
一.选择题(共7小题)
1.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
2.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20° B.40° C.60° D.70°
3.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS B.ASA C.SAS D.HL
4.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B′C′ B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
5.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是( )
A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B
6.如图,△ABC中,AC=BC,过点B作射线BF,在射线BF上取一点E,使得∠CBF=∠CAE,过点C作射线BF的垂线,垂足为点D,连接AE,若DE=a,AE=b,则BD的长度为( )
A.b B.a+b C.a+b D.2a+b
7.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH长为( )
A.3 B.4 C.5 D.6
二.填空题(共10小题)
8.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有 对.
9.如图,在△ABC中,∠ABC=2∠C,BQ和AP分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为 .
10.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是 秒.
11.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
12.一个三角形的两边长分别为2和4,则第三边上面的中线a的范围是 .
13.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
14.如图∠A=∠EGF,点F为BE与CG的中点,DB=4,DE=7,则EG长为 .
15.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD= .
16.如图,△ABC中,AB=AC,点D、E、F分别在AB、BC、CA边上,且BE=CF,BD=CE,如果∠A=44°,则∠EDF的度数为 .
17.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CF⊥AD,BE⊥AD.若CF=8,BE=6,AD=10,则EF的长为 .
三.解答题(共6小题)
18.如图,在五边形ABCDE中,AB=DE,AC=AD.
(1)请你添加一个与角有关的条件,使得△ABC≌△DEA,并说明理由;
(2)在(1)的条件下,若∠CAD=65°,∠B=110°,求∠BAE的度数.
19.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
20.如图,已知△ABC中,BE平分∠ABC,且BE=BA,点F是BE延长线上一点,且BF=BC,过点F作FD⊥BC于点D.
(1)求证:∠BEC=∠BAF;
(2)判断△AFC的形状并说明理由.
(3)若CD=2,求EF的长.
21.如图在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
(1)说明△ADE≌△BFE的理由;
(2)联结EG,那么EG与DF的位置关系是 ,请说明理由.
22.已知:DF∥BC,∠FDC=∠AEC.
(1)如图1,已知CD⊥AB,CB平分∠NCE.求∠ABC的度数;
(2)如图2,若∠ABC=∠ACF,AC=FC,DM=BE.求证:BC=MC.
23.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
参考答案
一.选择题(共7小题)
1.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
2.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
3.解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
4.解:A、由AB=A′B′,AC=A′C′,BC=B′C′可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故选:C.
5.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴2∠DFE=180°﹣∠FGC,
故选:C.
6.解:如图,连接CE,过点C作CM⊥AE交AE于M.
∵CD⊥BF,CM⊥AM,
∴∠CDB=∠M=90°,
在△CDB△CMA中,
,
∴△CDB≌△CMA(AAS),
∴CM=CD,BD=AM,
在Rt△CED和Rt△CEM,
,
∴Rt△CED≌Rt△CEM(HL),
∴DE=EM=a,
∴BD=AM=AE+EM=AE+DE=a+b,
故选:B.
7.解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
故选:B.
二.填空题(共10小题)
8.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
9.解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC①,
过点P作PD∥BQ交CQ于点D,如图,
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
∵AP=AP,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC②,
由①②得BQ+AQ=AB+BP,
∵△ABQ的周长为18,BP=4,
∴AB+BQ+AQ=AB+BP+AB=2AB+4=18,
∴AB=7.
10.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
11.解:①在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.
∴①正确;
没有条件可以证明CD=DN,
∴②错误;
∵△ABE≌△ACF,
∴AB=AC,
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),
∴③正确;
∵△ABE≌△ACF,
∴BE=CF,
∴④正确.
∴其中正确的结论有①③④.
故答案为:①③④.
12.解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵三角形两边长为2,4,第三边上的中线为a,
∴4﹣2<2a<4+2,即2<2a<6,
∴1<a<3.
故答案为:1<a<3.
13.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
14.解:∵∠A=∠EGF,∠AGD=∠EGF,
∴∠A=∠AGD,
∴AD=DG,
设AD=x,则DG=x,
在△EGF和△BCF中,
∵,
∴△EGF≌△BCF(SAS),
∴BC=EG,∠E=∠EBC,
∴EG∥BC,
∴∠AGD=∠C=∠A,
∴BC=AB=x+4=EG,
∵DE=7,
∴x+x+4=7,
x=,
∴EG=x+4=,
故答案为:.
15.证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
16.解:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=(180°﹣44°)=68°
∴∠1+∠2=180°﹣68°
∴∠3+∠2=180°﹣68°
∴∠DEF=68°,
∴∠EDF=.
故答案为:56°.
17.解:∵AB⊥CD,CF⊥AD,BE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,∠AEB=∠CFD=90°,
∴∠A=∠C,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF=6,AE=CF=8,
∵AF=AD﹣DF=10﹣6=4,
∴EF=AE﹣AF=8﹣4=4,
故答案为:4.
三.解答题(共6小题)
18.解:(1)添加一个角方面的条件为:∠BAC=∠EDA,使得△ABC≌△DEA,理由如下:
在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
(2)在(1)的条件下,
∵△ABC≌△DEA,
∴∠ACB=∠DAE,
∵∠CAD=65°,∠B=110°,
∴∠ACB+∠BAC=180°﹣∠B=70°,
∴∠DAE+∠BAC=∠ACB+∠BAC=70°,
∴∠BAE=∠DAE+∠BAC+∠CAD=70°+65°=135°.
19.(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
20.解:(1)∵BE平分∠ABC,
∴∠EBC=∠ABF,
在△BEC和△BAF中,
,
∴△BEC≌△BAF(SAS),
∴∠BEC=∠BAF;
(2)△AFC是等腰三角形.
证明:过F作FG⊥BA,与BA的延长线交于点G,如图,
∵BA=BE,BC=BF,∠ABF=∠CBF,
∴∠AEB=∠BCF,
∵∠BEC=∠BAF,
∴∠GAF=∠AEB=∠BCF,
∵BF平分∠ABC,FD⊥BC,FG⊥BA,
∴FD=FG,
在△CDF和△AGF中,
,
∴△CDF≌△AGF(AAS),
∴FC=FA,
∵△ACF是等腰三角形;
(3)设AB=BE=x,
∵△CDF≌△AGF,CD=2,
∴CD=AG=2,
∴BG=BA+AG=x+2,
在Rt△BFD和Rt△BFG中,
,
∴△BFD≌△BFG(HL),
∴BD=BG=x+2,
∴BF=BC=BD+CD=x+4,
∴EF=BF﹣BE=x+4﹣x=4.
21.解:(1)∵AD∥BC,
∴∠1=∠F,
∵E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
(2)如图,EG⊥DF,
∵∠1=∠F,∠1=∠2,
∴∠2=∠F,
∴DG=FG,
由(1)知:△ADE≌△BFE,
∴DE=EF,
∴EG⊥DF.
22.解:(1)∵DF∥BC,
∴∠FDC=∠NCB,
∵CB平分∠NCE,
∴∠NCB=∠BCE,
∵∠FDC=∠AEC,
∴∠FDC=∠NCB=∠BCE=∠AEC,
∵CD⊥AB,
∴∠ENC=90°,
∴∠AEC+∠NCE=∠AEC+∠BCE+∠NCB=3∠NCB=90°,
∴∠NCB=30°,
∴∠ABC=90°﹣∠NCB=60°;
(2)∵DF∥BC,
∴∠FMC=∠ACB,
∵∠ABC=∠ACF,
∴180°﹣∠FMC﹣∠ACF=180°﹣∠ACB﹣∠ABC,
即∠F=∠BAC,
在△DFC和△EAC中,
,
∴△DFC≌△EAC(AAS),
∴CD=CE,
在△MDC和△BEC中,
,
∴△MDC≌△BEC(SAS),
∴MC=BC.
23.解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
