人教版八年级 上册 第十二章 全等三角形的证明方法(AAS ASA HL)同步【教案】
文档属性
| 名称 | 人教版八年级 上册 第十二章 全等三角形的证明方法(AAS ASA HL)同步【教案】 |

|
|
| 格式 | zip | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览


文档简介
教案
学生姓名
性别
年级
八年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课共(
)次课
课时:
课时
教学课题
八年级
第十三章
全等三角形的证明方法(AAS
ASA
HL)
同步教案
教学目标
知识目标:掌握两个全等三角形的对应边、对应角的寻找规律。能力目标:全等三角形的证明方法(角角边、角边角、斜边直角边)。情感态度价值观:通过观察,想象图形的运动变化状况,确定对应关系。
教学重点与难点
证明直角三角形全等除了HL,还可把直角当一般角,用一般三角形全等的判定方法
教学过程知识梳理1、两个三角形全等的条件(3)全等三角形的判定3——角边角公理
两角和它们的夹边对应相等的两个三角形全等.简写为“角边角”或“ASA”.
(4)全等三角形的判定4——角角边推论 两角和其中一角的对边对应相等的两个三角形全等.简称“角角边”“AAS”.
(5)直角三角形全等的判定——斜边直角边公理 斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边直角边”或“HL”.
判定直角三角形全等的方法:
①一般三角形全等的判定方法都适用;②斜边-直角边公理2、寻找对应元素的方法(1)根据对应顶点找如果两个三角形全等,那么,以对应顶点为顶点的角是对应角;以对应顶点为端点的边是对应边。通常情况下,两个三角形全等时,对应顶点的字母都写在对应的位置上,因此,由全等三角形的记法便可写出对应的元素。(2)根据已知的对应元素寻找全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(3)通过观察,想象图形的运动变化状况,确定对应关系。通过对两个全等三角形各种不同位置关系的观察和分析,可以看出其中一个是由另一个经过下列各种运动而形成的。3、注意问题:(1)在判定两个三角形全等时,至少有一边对应相等;(2)不能证明两个三角形全等的是,a:
三个角对应相等,即AAA;b
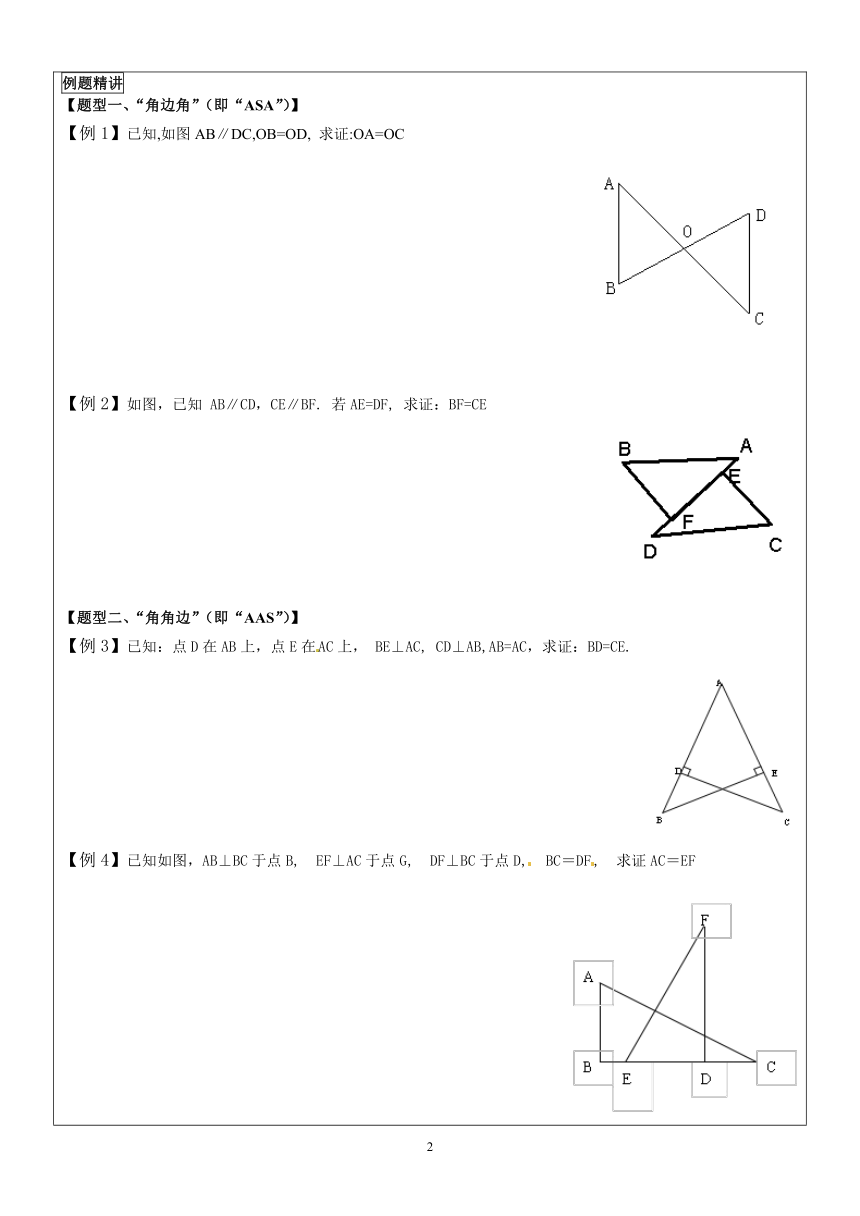
:有两边和其中一角对应相等,即SSA。例题精讲【题型一、“角边角”(即“ASA”)】【例1】已知,如图AB∥DC,OB=OD,
求证:OA=OC
【例2】如图,已知
AB∥CD,CE∥BF.
若AE=DF,
求证:BF=CE
【题型二、“角角边”(即“AAS”)】【例3】已知:点D在AB上,点E在AC上,
BE⊥AC,
CD⊥AB,AB=AC,求证:BD=CE.
【例4】已知如图,AB⊥BC于点B,
EF⊥AC于点G,
DF⊥BC于点D,
BC=DF,
求证AC=EF
【题型三、“直角三角形全等”的判定(即“HL”)】【例5】如图,AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.求证:(1)△BFD≌△ACD;(2)BE⊥AC.
【例6】如图,CD⊥AB,BE⊥AC,OB=OC.求证:∠1=∠2.
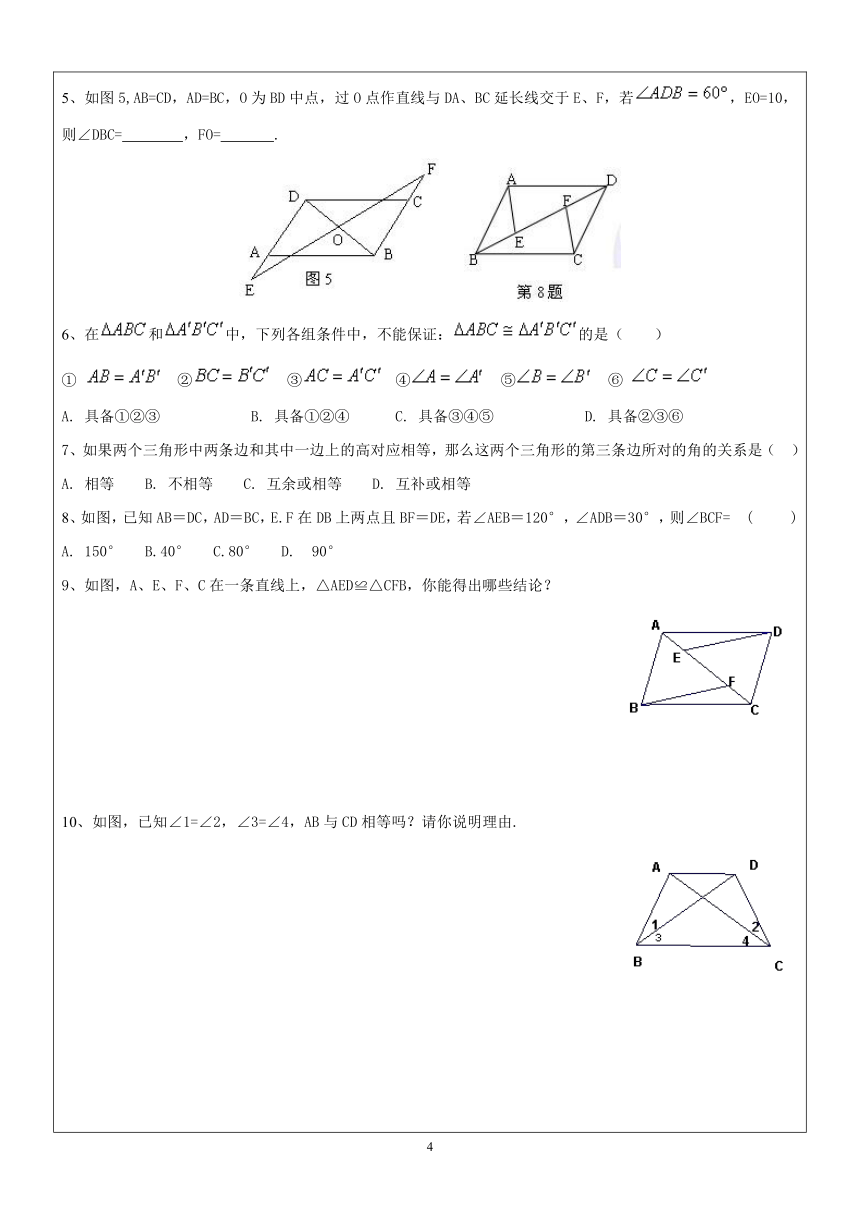
巩固练习1、如图1,若△ABC≌△ADE,∠EAC=35°,则∠BAD=_________度.2、如图2,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.3、已知:如图3,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“SAS”为依据,还须添加的一个条件为________________.(2)若以“ASA”为依据,还须添加的一个条件为________________.(3)若以“AAS”为依据,还须添加的一个条件为________________.4、如图4,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则△______≌△_______.5、如图5,AB=CD,AD=BC,O为BD中点,过O点作直线与DA、BC延长线交于E、F,若,EO=10,则∠DBC=
,FO=
.
6、在和中,下列各组条件中,不能保证:的是(
)①
②
③
④
⑤
⑥
A.
具备①②③
B.
具备①②④
C.
具备③④⑤
D.
具备②③⑥7、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是(
)A.
相等
B.
不相等
C.
互余或相等
D.
互补或相等8、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=
(
)A.
150°
B.40°
C.80°
D.
90°9、如图,A、E、F、C在一条直线上,△AED≌△CFB,你能得出哪些结论?
10、如图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
11、如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?
12、已知如图,E,F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分.
课后作业【基础巩固】1、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是(
)A.相等
B.不相等
C.互余或相等
D.互补或相等2、如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=(
)A.25°
B.27°
C.30°
D.45°
3、如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(
)A.
SSS
B.
SAS
C.
AAS
D.
ASA
4、将一张长方形纸片按如图所示的方式折叠,为折痕,则的度数为(
)A.60°
B.75°
C.90° D.95°5、如图,已知∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是________度;6、△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
;7.如图:将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A=
度;8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,CD=2
cm,则点D到BA的距离为________cm.9、已知:
BE⊥CD,DF⊥BC,BC=DA,求证:△BEC≌△DAE10、如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.11、如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.12、如图,点A、C、B、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.【能力提升】13、如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF.交AB于E,交BC于F,若AE=4,FC=3,求EF的长.14、已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.(1)求证:△ABC是等腰三角形;(2)判断点O是否在∠BAC的角平分线上,并说明理由.15、如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE。求证:△ACD≌△CBE.
B
C
D
E
F
A
学生姓名
性别
年级
八年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课共(
)次课
课时:
课时
教学课题
八年级
第十三章
全等三角形的证明方法(AAS
ASA
HL)
同步教案
教学目标
知识目标:掌握两个全等三角形的对应边、对应角的寻找规律。能力目标:全等三角形的证明方法(角角边、角边角、斜边直角边)。情感态度价值观:通过观察,想象图形的运动变化状况,确定对应关系。
教学重点与难点
证明直角三角形全等除了HL,还可把直角当一般角,用一般三角形全等的判定方法
教学过程知识梳理1、两个三角形全等的条件(3)全等三角形的判定3——角边角公理
两角和它们的夹边对应相等的两个三角形全等.简写为“角边角”或“ASA”.
(4)全等三角形的判定4——角角边推论 两角和其中一角的对边对应相等的两个三角形全等.简称“角角边”“AAS”.
(5)直角三角形全等的判定——斜边直角边公理 斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边直角边”或“HL”.
判定直角三角形全等的方法:
①一般三角形全等的判定方法都适用;②斜边-直角边公理2、寻找对应元素的方法(1)根据对应顶点找如果两个三角形全等,那么,以对应顶点为顶点的角是对应角;以对应顶点为端点的边是对应边。通常情况下,两个三角形全等时,对应顶点的字母都写在对应的位置上,因此,由全等三角形的记法便可写出对应的元素。(2)根据已知的对应元素寻找全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(3)通过观察,想象图形的运动变化状况,确定对应关系。通过对两个全等三角形各种不同位置关系的观察和分析,可以看出其中一个是由另一个经过下列各种运动而形成的。3、注意问题:(1)在判定两个三角形全等时,至少有一边对应相等;(2)不能证明两个三角形全等的是,a:
三个角对应相等,即AAA;b
:有两边和其中一角对应相等,即SSA。例题精讲【题型一、“角边角”(即“ASA”)】【例1】已知,如图AB∥DC,OB=OD,
求证:OA=OC
【例2】如图,已知
AB∥CD,CE∥BF.
若AE=DF,
求证:BF=CE
【题型二、“角角边”(即“AAS”)】【例3】已知:点D在AB上,点E在AC上,
BE⊥AC,
CD⊥AB,AB=AC,求证:BD=CE.
【例4】已知如图,AB⊥BC于点B,
EF⊥AC于点G,
DF⊥BC于点D,
BC=DF,
求证AC=EF
【题型三、“直角三角形全等”的判定(即“HL”)】【例5】如图,AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.求证:(1)△BFD≌△ACD;(2)BE⊥AC.
【例6】如图,CD⊥AB,BE⊥AC,OB=OC.求证:∠1=∠2.
巩固练习1、如图1,若△ABC≌△ADE,∠EAC=35°,则∠BAD=_________度.2、如图2,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.3、已知:如图3,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“SAS”为依据,还须添加的一个条件为________________.(2)若以“ASA”为依据,还须添加的一个条件为________________.(3)若以“AAS”为依据,还须添加的一个条件为________________.4、如图4,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则△______≌△_______.5、如图5,AB=CD,AD=BC,O为BD中点,过O点作直线与DA、BC延长线交于E、F,若,EO=10,则∠DBC=
,FO=
.
6、在和中,下列各组条件中,不能保证:的是(
)①
②
③
④
⑤
⑥
A.
具备①②③
B.
具备①②④
C.
具备③④⑤
D.
具备②③⑥7、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是(
)A.
相等
B.
不相等
C.
互余或相等
D.
互补或相等8、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=
(
)A.
150°
B.40°
C.80°
D.
90°9、如图,A、E、F、C在一条直线上,△AED≌△CFB,你能得出哪些结论?
10、如图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
11、如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?
12、已知如图,E,F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分.
课后作业【基础巩固】1、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是(
)A.相等
B.不相等
C.互余或相等
D.互补或相等2、如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=(
)A.25°
B.27°
C.30°
D.45°
3、如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(
)A.
SSS
B.
SAS
C.
AAS
D.
ASA
4、将一张长方形纸片按如图所示的方式折叠,为折痕,则的度数为(
)A.60°
B.75°
C.90° D.95°5、如图,已知∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是________度;6、△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
;7.如图:将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A=
度;8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,CD=2
cm,则点D到BA的距离为________cm.9、已知:
BE⊥CD,DF⊥BC,BC=DA,求证:△BEC≌△DAE10、如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.11、如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.12、如图,点A、C、B、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.【能力提升】13、如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF.交AB于E,交BC于F,若AE=4,FC=3,求EF的长.14、已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.(1)求证:△ABC是等腰三角形;(2)判断点O是否在∠BAC的角平分线上,并说明理由.15、如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE。求证:△ACD≌△CBE.
B
C
D
E
F
A
