2020-2021学年河北省唐山市滦南县七年级(下)期末数学试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年河北省唐山市滦南县七年级(下)期末数学试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览



文档简介
2020-2021学年河北省唐山市滦南县七年级(下)期末数学试卷
一、选择题(本大题共有16个小题,共42分。1~10小题各3分,11~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.按语句画图:点P在直线a上,也在直线b上,但不在直线c上,直线a,b,c两两相交.正确的是( )
A. B.
C. D.
2.给出下列等式,其中正确的是( )
A.a3?a2=a6 B.a3÷a﹣2=a
C.a﹣5=(a3)﹣2 D.1a3b3=(ab)﹣3
3.已知三角形的两边长分别是4和9,则此三角形第三边的长可以是( )
A.4 B.5 C.10 D.15
4.2020年11月24日22时6分,嫦娥5号实现了飞行过程中第一次轨道修正后继续飞向月球.截至当时,嫦娥5号距离地球约16000公里,其中160000用科学记数法表示为( )
A.0.16×106 B.1.6×105 C.1.6×104 D.16×104
5.若x|a|﹣1+(a﹣2)y=1是关于x,y的二元一次方程,则a=( )
A.2 B.﹣2 C.2或﹣2 D.0
6.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2;
②∠1=∠3;
③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°
A.①②③ B.①②④ C.①④⑤ D.②③⑤
7.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.1﹣2a>1﹣2b D.a﹣3>b﹣3
8.若方程mx+ny=6有两个解x=-2y=3和x=3y=-2,则m+n的值为( )
A.12 B.﹣12 C.6 D.﹣6
9.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示.已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.42° B.39° C.38° D.36°
10.下列多项式:①x2+y2;
②﹣x2﹣4y2;
③﹣1+a2;
④b2﹣a2.其中能用平方差公式分解因式的多项式有( )
A.1个 B.2个 C.3个 D.4个
11.不等式2x﹣3≤1得解集在以下数轴表示中,正确的是( )
A. B.
C. D.
12.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线.若△ABD的周长为30,则△BCD的周长是( )
A.20 B.24 C.26 D.28
13.若多项式x2﹣mx+n可因式分解为(x+3)(x﹣4).其中m,n均为整数,则m﹣n的值是( )
A.13 B.11 C.9 D.7
14.如图,平移△ABC得到△DEF,其中点A的对应点是点D,则下列结论中不成立的是( )
A.AD∥BE B.∠BAC=∠DFE C.AC=DF D.∠ABC=∠DEF
15.如果不等式组x+2a≥42x-b3<1的解集是0≤x<1,那么a+b的值为( )
A.﹣1 B.0 C.1 D.2
16.已知a,b,c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
二、填空题(本大题共有4个小题,共14分17~18小题3分,19~20小题每空2分)
17.因式分解:ab3﹣4ab2+4ab= .
18.已知:m+2n﹣3=0,则2m?4n的值为 .
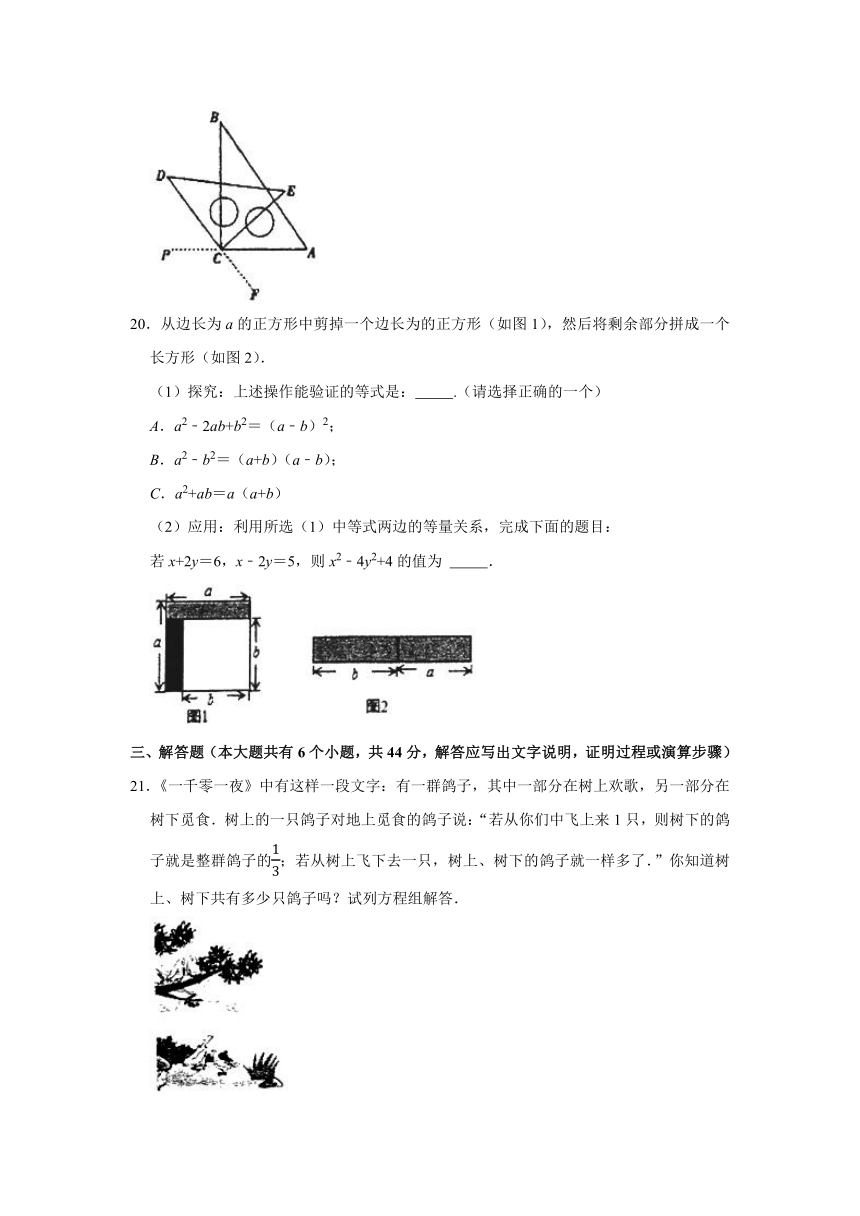
19.小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示.延长DC至点F,∠PCD与∠ACF就是一组对顶角.
(1)若∠ACF=30°,则∠PCD= ;
(2)若重叠所成的∠BCE=n°(0<n<90),则∠PCF的度数 .
20.从边长为a的正方形中剪掉一个边长为的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是: .(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2;
B.a2﹣b2=(a+b)(a﹣b);
C.a2+ab=a(a+b)
(2)应用:利用所选(1)中等式两边的等量关系,完成下面的题目:
若x+2y=6,x﹣2y=5,则x2﹣4y2+4的值为 .
三、解答题(本大题共有6个小题,共44分,解答应写出文字说明,证明过程或演算步骤)
21.《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在树下觅食.树上的一只鸽子对地上觅食的鸽子说:“若从你们中飞上来1只,则树下的鸽子就是整群鸽子的13;若从树上飞下去一只,树上、树下的鸽子就一样多了.”你知道树上、树下共有多少只鸽子吗?试列方程组解答.
22.结合下面命题的说理过程填写依据.
已知:如图,AB∥DN,∠ABC=∠DEF.
则BC∥ME.试说明理由.
理由:因为AB∥DN( )
所以∠ABC=∠DNC,( )
又因为∠ABC=∠DEF(已知)
所以∠DNC=∠DEF( )
所以BC∥MF( ).
23.解不等式组,并把它的解集在数轴上表示出来.
x-2(x-1)≥1①1+x2>x-1②.
24.利用分解因式,有时能进行简便计算.
例1 98×12=(100﹣2)×12=1200﹣24=1176;
例2﹣16×233+17×233=(﹣16+17)×233=233.
请你参考黑板中老师的讲解,用因式分解进行简便计算:
(1)999×(﹣15);
(2)999×11845+999×(-15)﹣999×1835.
25.随着一代人的老去,社会消费结构也将改变,新生代年轻人正在不断抬升消费倾向.他们追求住房、交通通信、教育、文娱,尤其是网游、运动等服务消费和新型消费,必将使消费结构出现新的变化.比如:年轻人几乎都有学车、购车、驾车旅游的消费需求,因此汽车租赁就为这种消费升级创造了条件.已知一青年欲租用一辆汽车,现有甲、乙两家出租公司,甲公司的出租条件为汽车每行驶1km需付租车费1.10元;乙公司的出租条件为每月付3000元租车费另外,汽车每行驶1km,租车人需再付0.10元汽车磨损费.那么这个年轻人怎样租车比较合算?
26.冀教版义务教育七下第14页有这样一个问题:如图1,在△ABC中,∠A=40°,外角平分线BN和CN相交于点N,求∠BNC的度数.
请你先完成这个问题的解答.
嘉琪在完成以上问题的解答后,作如下变式探究:
(2)如图2,在△ABC中,∠A=80°,若∠CBN=38∠CBE,∠BCM=38∠BCD,BN与CM交于点O,则∠BOC的度数是 .
(3)如图3,在△ABC中,∠A=n°,若∠CBN=34∠CBE,∠BCM=34∠BCD,当射线CM与BN相交时,n的取值范围是什么?试说明理由.
七年级数学参考答案及评分标准
一、选择题(本大题共有16个小题,共42分.1~10小题各3分,11~16小题各2分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
A
D
C
B
B
D
C
A
D
B
C
B
A
B
C
A
二、填空题(本大题共有4个小题,共14分,17~18小题3分,19~20小题每空2分)
17.ab(b-2)2 18.8 19.(1)30°;(2)180°-n°
20.(1)B;(2)34
三、解答题(本大题共有6个小题,共44分,解答应写出文字说明,证明过程或演算步骤)
21.(6分)
解:设树上有x只鸽子,树下有y只鸽子.则树上、树下共有(x+y)只鸽子.……1分
依题意可得 ………………………………………………………3分
解得 …………………………………………………………………………4分
所以树上、树下共有12只鸽子.……………………………………………………5分
答:树上、树下共有12只鸽子.…………………………………………………………6分
22.(6分)
解:已知 ……………………………………………………………………………………1分
两直线平行,同位角相等 ……………………………………………………………3分
等量代换 ………………………………………………………………………………4分
同位角相等,两直线平行………………………………………………………………6分
23.(7分)
解:由①得 x-2x+2≥1, 解得:x≤1, …………………………………………2分
由②得 1+x>2x-2, 解得:x<3, …………………………………………4分
所以不等式组的解集为x≤1. …………………………………6分
其解集在数轴上的表示如下:
………………………………………………7分
24.(7分)
解:(1)原式 ……………………………………………………2分
. ……………………………………………………………3分
(2)原式 …………………………………………5分
. ………………………………………………………………7分
25.(8分)
解:设汽车行驶的路程为xkm. …………………………………………………………1分
则甲公司所需费用为1.1x元,乙公司所需费用为(3000+0.1x)元.………… 2分
(1)当1.1x<(3000+0.1x)时,解得:x<3000; ……………………………3分
(2)当1.1x=(3000+0.1x)时,解得:x=3000; ……………………………4分
(3)当1.1x>(3000+0.1x)时,解得:x>3000. ……………………………5分
所以汽车每月的行驶里程小于3000km时,租甲公司的车合算; ………………6分
汽车每月的行驶里程等于3000km时,租甲、乙公司的车费用一样; ……7分
汽车每月的行驶里程大于3000km时,租乙公司的车合算. ………………8分
26.(10分)
解:(1)由于△ABC外角平分线BN和CN相交于点N,
所以∠BCN=(∠A+∠ABC),∠CBN=(∠A+∠ACB)…………2分
所以∠BCN+∠CBN=(∠A+∠ABC+∠ACB)+∠A
=90°+20°=110°. …………………………………………3分
所以∠BOC=180°-(∠BCN+∠CBN)=70°. …………………………4分
(2)82.5° ………………………………………………………………………………6分
因为∠CBN=∠CBE,∠BCM=∠BCD,
所以∠CBN+∠BCM=(∠A+∠ABC+∠ACB)+∠A
=×180°+×80°=×260°
所以∠BOC=180°-×260°=82.5°
(3)因为∠CBN=∠CBE,∠BCM=∠BCD,
所以∠CBN+∠BCM=(∠A+∠ABC+∠ACB)+∠A
=135°+n° ………………………………………………7分
所以∠BOC=45°-n°, ……………………………………………………8分
当射线CM与BN相交时,45°-n°>0°,解得n<60. …………………9分
所以n的取值范围是0<n<60. ……………………………………………10分
一、选择题(本大题共有16个小题,共42分。1~10小题各3分,11~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.按语句画图:点P在直线a上,也在直线b上,但不在直线c上,直线a,b,c两两相交.正确的是( )
A. B.
C. D.
2.给出下列等式,其中正确的是( )
A.a3?a2=a6 B.a3÷a﹣2=a
C.a﹣5=(a3)﹣2 D.1a3b3=(ab)﹣3
3.已知三角形的两边长分别是4和9,则此三角形第三边的长可以是( )
A.4 B.5 C.10 D.15
4.2020年11月24日22时6分,嫦娥5号实现了飞行过程中第一次轨道修正后继续飞向月球.截至当时,嫦娥5号距离地球约16000公里,其中160000用科学记数法表示为( )
A.0.16×106 B.1.6×105 C.1.6×104 D.16×104
5.若x|a|﹣1+(a﹣2)y=1是关于x,y的二元一次方程,则a=( )
A.2 B.﹣2 C.2或﹣2 D.0
6.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2;
②∠1=∠3;
③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°
A.①②③ B.①②④ C.①④⑤ D.②③⑤
7.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.1﹣2a>1﹣2b D.a﹣3>b﹣3
8.若方程mx+ny=6有两个解x=-2y=3和x=3y=-2,则m+n的值为( )
A.12 B.﹣12 C.6 D.﹣6
9.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示.已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.42° B.39° C.38° D.36°
10.下列多项式:①x2+y2;
②﹣x2﹣4y2;
③﹣1+a2;
④b2﹣a2.其中能用平方差公式分解因式的多项式有( )
A.1个 B.2个 C.3个 D.4个
11.不等式2x﹣3≤1得解集在以下数轴表示中,正确的是( )
A. B.
C. D.
12.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线.若△ABD的周长为30,则△BCD的周长是( )
A.20 B.24 C.26 D.28
13.若多项式x2﹣mx+n可因式分解为(x+3)(x﹣4).其中m,n均为整数,则m﹣n的值是( )
A.13 B.11 C.9 D.7
14.如图,平移△ABC得到△DEF,其中点A的对应点是点D,则下列结论中不成立的是( )
A.AD∥BE B.∠BAC=∠DFE C.AC=DF D.∠ABC=∠DEF
15.如果不等式组x+2a≥42x-b3<1的解集是0≤x<1,那么a+b的值为( )
A.﹣1 B.0 C.1 D.2
16.已知a,b,c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
二、填空题(本大题共有4个小题,共14分17~18小题3分,19~20小题每空2分)
17.因式分解:ab3﹣4ab2+4ab= .
18.已知:m+2n﹣3=0,则2m?4n的值为 .
19.小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示.延长DC至点F,∠PCD与∠ACF就是一组对顶角.
(1)若∠ACF=30°,则∠PCD= ;
(2)若重叠所成的∠BCE=n°(0<n<90),则∠PCF的度数 .
20.从边长为a的正方形中剪掉一个边长为的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是: .(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2;
B.a2﹣b2=(a+b)(a﹣b);
C.a2+ab=a(a+b)
(2)应用:利用所选(1)中等式两边的等量关系,完成下面的题目:
若x+2y=6,x﹣2y=5,则x2﹣4y2+4的值为 .
三、解答题(本大题共有6个小题,共44分,解答应写出文字说明,证明过程或演算步骤)
21.《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在树下觅食.树上的一只鸽子对地上觅食的鸽子说:“若从你们中飞上来1只,则树下的鸽子就是整群鸽子的13;若从树上飞下去一只,树上、树下的鸽子就一样多了.”你知道树上、树下共有多少只鸽子吗?试列方程组解答.
22.结合下面命题的说理过程填写依据.
已知:如图,AB∥DN,∠ABC=∠DEF.
则BC∥ME.试说明理由.
理由:因为AB∥DN( )
所以∠ABC=∠DNC,( )
又因为∠ABC=∠DEF(已知)
所以∠DNC=∠DEF( )
所以BC∥MF( ).
23.解不等式组,并把它的解集在数轴上表示出来.
x-2(x-1)≥1①1+x2>x-1②.
24.利用分解因式,有时能进行简便计算.
例1 98×12=(100﹣2)×12=1200﹣24=1176;
例2﹣16×233+17×233=(﹣16+17)×233=233.
请你参考黑板中老师的讲解,用因式分解进行简便计算:
(1)999×(﹣15);
(2)999×11845+999×(-15)﹣999×1835.
25.随着一代人的老去,社会消费结构也将改变,新生代年轻人正在不断抬升消费倾向.他们追求住房、交通通信、教育、文娱,尤其是网游、运动等服务消费和新型消费,必将使消费结构出现新的变化.比如:年轻人几乎都有学车、购车、驾车旅游的消费需求,因此汽车租赁就为这种消费升级创造了条件.已知一青年欲租用一辆汽车,现有甲、乙两家出租公司,甲公司的出租条件为汽车每行驶1km需付租车费1.10元;乙公司的出租条件为每月付3000元租车费另外,汽车每行驶1km,租车人需再付0.10元汽车磨损费.那么这个年轻人怎样租车比较合算?
26.冀教版义务教育七下第14页有这样一个问题:如图1,在△ABC中,∠A=40°,外角平分线BN和CN相交于点N,求∠BNC的度数.
请你先完成这个问题的解答.
嘉琪在完成以上问题的解答后,作如下变式探究:
(2)如图2,在△ABC中,∠A=80°,若∠CBN=38∠CBE,∠BCM=38∠BCD,BN与CM交于点O,则∠BOC的度数是 .
(3)如图3,在△ABC中,∠A=n°,若∠CBN=34∠CBE,∠BCM=34∠BCD,当射线CM与BN相交时,n的取值范围是什么?试说明理由.
七年级数学参考答案及评分标准
一、选择题(本大题共有16个小题,共42分.1~10小题各3分,11~16小题各2分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
A
D
C
B
B
D
C
A
D
B
C
B
A
B
C
A
二、填空题(本大题共有4个小题,共14分,17~18小题3分,19~20小题每空2分)
17.ab(b-2)2 18.8 19.(1)30°;(2)180°-n°
20.(1)B;(2)34
三、解答题(本大题共有6个小题,共44分,解答应写出文字说明,证明过程或演算步骤)
21.(6分)
解:设树上有x只鸽子,树下有y只鸽子.则树上、树下共有(x+y)只鸽子.……1分
依题意可得 ………………………………………………………3分
解得 …………………………………………………………………………4分
所以树上、树下共有12只鸽子.……………………………………………………5分
答:树上、树下共有12只鸽子.…………………………………………………………6分
22.(6分)
解:已知 ……………………………………………………………………………………1分
两直线平行,同位角相等 ……………………………………………………………3分
等量代换 ………………………………………………………………………………4分
同位角相等,两直线平行………………………………………………………………6分
23.(7分)
解:由①得 x-2x+2≥1, 解得:x≤1, …………………………………………2分
由②得 1+x>2x-2, 解得:x<3, …………………………………………4分
所以不等式组的解集为x≤1. …………………………………6分
其解集在数轴上的表示如下:
………………………………………………7分
24.(7分)
解:(1)原式 ……………………………………………………2分
. ……………………………………………………………3分
(2)原式 …………………………………………5分
. ………………………………………………………………7分
25.(8分)
解:设汽车行驶的路程为xkm. …………………………………………………………1分
则甲公司所需费用为1.1x元,乙公司所需费用为(3000+0.1x)元.………… 2分
(1)当1.1x<(3000+0.1x)时,解得:x<3000; ……………………………3分
(2)当1.1x=(3000+0.1x)时,解得:x=3000; ……………………………4分
(3)当1.1x>(3000+0.1x)时,解得:x>3000. ……………………………5分
所以汽车每月的行驶里程小于3000km时,租甲公司的车合算; ………………6分
汽车每月的行驶里程等于3000km时,租甲、乙公司的车费用一样; ……7分
汽车每月的行驶里程大于3000km时,租乙公司的车合算. ………………8分
26.(10分)
解:(1)由于△ABC外角平分线BN和CN相交于点N,
所以∠BCN=(∠A+∠ABC),∠CBN=(∠A+∠ACB)…………2分
所以∠BCN+∠CBN=(∠A+∠ABC+∠ACB)+∠A
=90°+20°=110°. …………………………………………3分
所以∠BOC=180°-(∠BCN+∠CBN)=70°. …………………………4分
(2)82.5° ………………………………………………………………………………6分
因为∠CBN=∠CBE,∠BCM=∠BCD,
所以∠CBN+∠BCM=(∠A+∠ABC+∠ACB)+∠A
=×180°+×80°=×260°
所以∠BOC=180°-×260°=82.5°
(3)因为∠CBN=∠CBE,∠BCM=∠BCD,
所以∠CBN+∠BCM=(∠A+∠ABC+∠ACB)+∠A
=135°+n° ………………………………………………7分
所以∠BOC=45°-n°, ……………………………………………………8分
当射线CM与BN相交时,45°-n°>0°,解得n<60. …………………9分
所以n的取值范围是0<n<60. ……………………………………………10分
同课章节目录
