4.3.1空间直角坐标系
图片预览



文档简介
(共17张PPT)
4.3.1 空间直角坐标系
问题引入
1.数轴Ox上的点M,用代数的方法怎样表示呢?
2.直角坐标平面上的点M,怎样表示呢?
数轴Ox上的点M,可用与它对应的实数x表示;
直角坐标平面上的点M,可用一对有序实数(x,y)表示.
x
O
y
A
O
x
x
M
(x,y)
x
y
问题引入
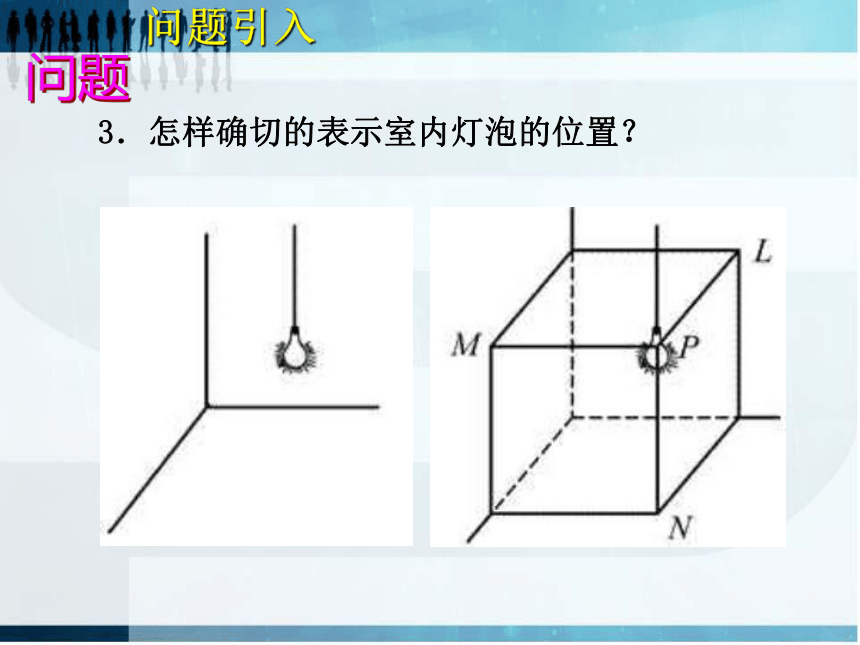
3.怎样确切的表示室内灯泡的位置?
问题引入
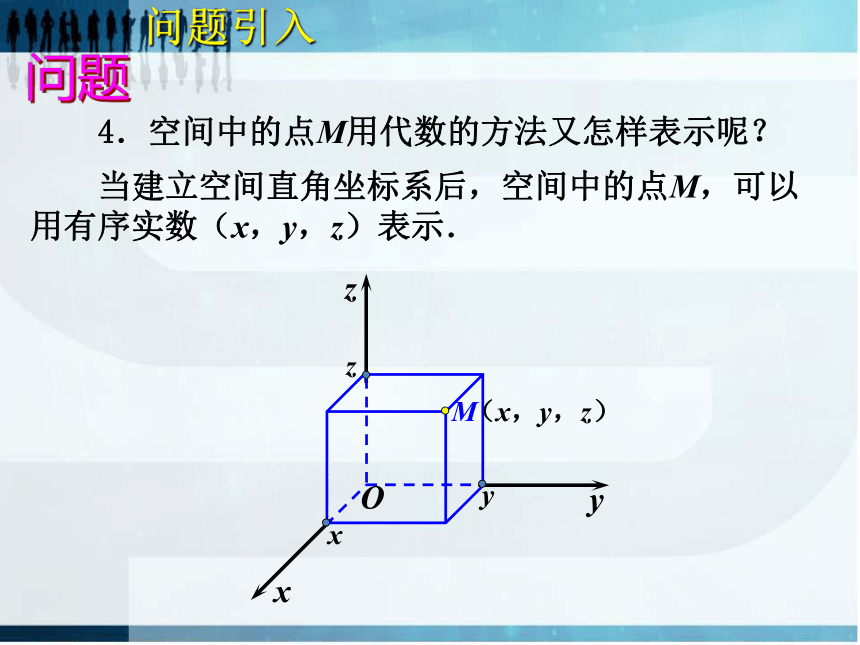
4.空间中的点M用代数的方法又怎样表示呢?
当建立空间直角坐标系后,空间中的点M,可以用有序实数(x,y,z)表示.
O
y
x
z
M
x
y
z
(x,y,z)
y
x
z
如图, 是单位正方体.以O为原点,分别以射线OA,OC, 的方向为正方向,以线段OA,OC,
的长为单位长,建立三条数轴:x轴、y 轴、z 轴.这时我们说建立了一个空间直角坐标系 ,其中点O 叫做坐标原点, x轴、y 轴、z 轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
空间直角坐标系
A
B
C
O
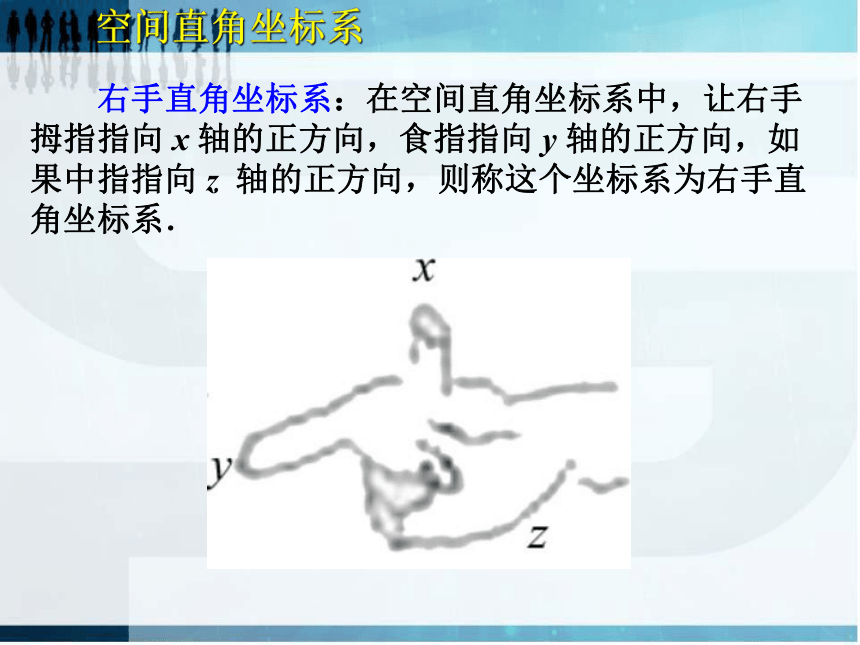
右手直角坐标系:在空间直角坐标系中,让右手拇指指向 x 轴的正方向,食指指向 y 轴的正方向,如果中指指向 z 轴的正方向,则称这个坐标系为右手直角坐标系.
空间直角坐标系
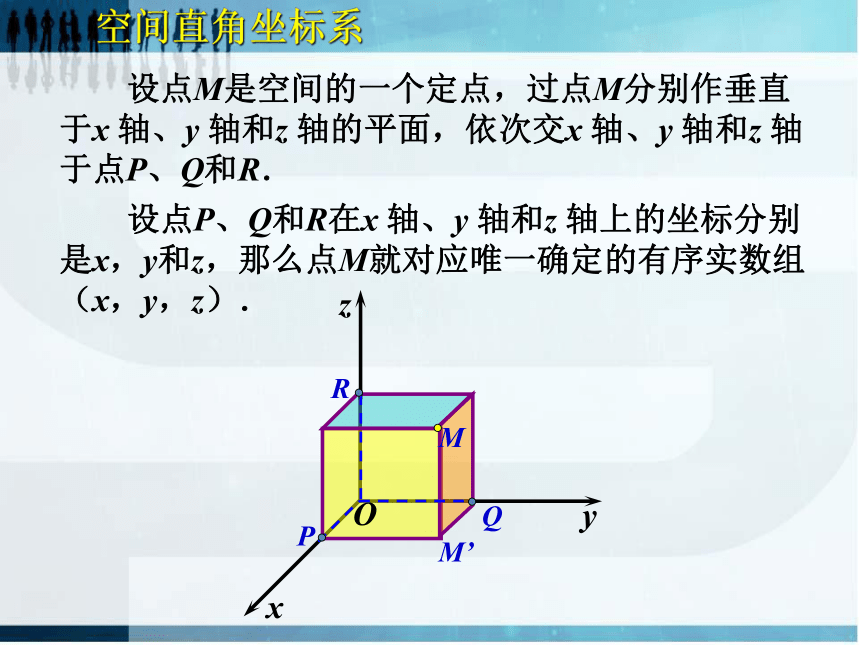
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
空间直角坐标系
y
x
z
M’
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
M
R
Q
P
反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
空间直角坐标系
y
x
z
M’
O
M
R
Q
P
空间直角坐标系
y
x
z
P
M’
Q
O
M
R
这样空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.
y
x
z
A
B
C
O
OABC—A’B’C’D’是单位正方体.以O为原点,分别以射线OA,OC, OD’的方向为正方向,以线段OA,OC, OD’的长为单位长,建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标.并指出哪些点在坐标轴上,哪些点在坐标平面上.
空间直角坐标系
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
例1 如下图,在长方体 中, , , 写出四点D’,C,A’,B’的坐标.
解: 在z 轴上,且 ,它的竖坐标是2;它的横坐标x与纵坐标y都是零,所以点 的坐标是(0,0,2).
点C 在y 轴上,且 ,它的纵坐标是4;它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).
同理,点 的坐标是(3,0,2).
O
y
x
z
A
C
B
典型例题
例1 如下图,在长方体 中, , , 写出四点D’,C,A’,B’的坐标.
O
y
x
z
A
C
B
典型例题
解:点B’在平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y 相同.在xOy平面上,点B 横坐标x=3,纵坐标y=4;点B’在z轴上的射影是D’,它的竖坐标与点D’的竖坐标相同,点D’的竖坐标z=2.
所以点B’的坐标是(3,4,2).
例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
典型例题
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
典型例题
如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.
x
y
z
O
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1).
中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );
典型例题
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0),
( , ,0).
x
y
z
O
知识小结
空间直角坐标系
点在空间直角坐标系中的坐标
4.3.1 空间直角坐标系
问题引入
1.数轴Ox上的点M,用代数的方法怎样表示呢?
2.直角坐标平面上的点M,怎样表示呢?
数轴Ox上的点M,可用与它对应的实数x表示;
直角坐标平面上的点M,可用一对有序实数(x,y)表示.
x
O
y
A
O
x
x
M
(x,y)
x
y
问题引入
3.怎样确切的表示室内灯泡的位置?
问题引入
4.空间中的点M用代数的方法又怎样表示呢?
当建立空间直角坐标系后,空间中的点M,可以用有序实数(x,y,z)表示.
O
y
x
z
M
x
y
z
(x,y,z)
y
x
z
如图, 是单位正方体.以O为原点,分别以射线OA,OC, 的方向为正方向,以线段OA,OC,
的长为单位长,建立三条数轴:x轴、y 轴、z 轴.这时我们说建立了一个空间直角坐标系 ,其中点O 叫做坐标原点, x轴、y 轴、z 轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
空间直角坐标系
A
B
C
O
右手直角坐标系:在空间直角坐标系中,让右手拇指指向 x 轴的正方向,食指指向 y 轴的正方向,如果中指指向 z 轴的正方向,则称这个坐标系为右手直角坐标系.
空间直角坐标系
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
空间直角坐标系
y
x
z
M’
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
M
R
Q
P
反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
空间直角坐标系
y
x
z
M’
O
M
R
Q
P
空间直角坐标系
y
x
z
P
M’
Q
O
M
R
这样空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.
y
x
z
A
B
C
O
OABC—A’B’C’D’是单位正方体.以O为原点,分别以射线OA,OC, OD’的方向为正方向,以线段OA,OC, OD’的长为单位长,建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标.并指出哪些点在坐标轴上,哪些点在坐标平面上.
空间直角坐标系
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
例1 如下图,在长方体 中, , , 写出四点D’,C,A’,B’的坐标.
解: 在z 轴上,且 ,它的竖坐标是2;它的横坐标x与纵坐标y都是零,所以点 的坐标是(0,0,2).
点C 在y 轴上,且 ,它的纵坐标是4;它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).
同理,点 的坐标是(3,0,2).
O
y
x
z
A
C
B
典型例题
例1 如下图,在长方体 中, , , 写出四点D’,C,A’,B’的坐标.
O
y
x
z
A
C
B
典型例题
解:点B’在平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y 相同.在xOy平面上,点B 横坐标x=3,纵坐标y=4;点B’在z轴上的射影是D’,它的竖坐标与点D’的竖坐标相同,点D’的竖坐标z=2.
所以点B’的坐标是(3,4,2).
例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
典型例题
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.
典型例题
如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.
x
y
z
O
上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1).
中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );
典型例题
下层的原子全部在平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0),
( , ,0).
x
y
z
O
知识小结
空间直角坐标系
点在空间直角坐标系中的坐标
