9.2.4 总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(含解析)
文档属性
| 名称 | 9.2.4 总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 287.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览



文档简介
9.2.4 总体离散程度的估计-【新教材】人教A版(2019)高中数学必修第二册同步练习(含解析)
学校:___________姓名:___________班级:___________学号:___________
一.选择题
小明5天上学途中所花的时间(单位:分钟)分别为12,8,10,9,11,则这组数据的方差为(? ? ? ?)
A. 4 B. 2 C. 9 D. 3
在某次测量中得到的A样本数据如下:22,23,25,26,31,30;若B样本数据恰好是A样本数据每个数都减
去10后所得的数据,则A,B两样本的下列数字特征相同的是(????)
A. 方差 B. 平均数 C. 众数 D. 中位数
某农科所种植的甲、乙两种水稻,连续六年在面积相等的两块稻田中作对比试验,试验得出平均产量是x甲=x乙=415㎏,方差是s甲2=794,s乙2=958,那么这两个水稻品种中产量比较稳定的是(????)
A. 甲 B. 乙
C. 甲、乙一样稳定 D. 无法确定
已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是13,那么另一组数3x1?2,3x2?2,3x3?2,3x4?2,3x5?2的平均数,方差分别是(????)
A. 2,13 B. 2,1 C. 4,3 D. 4,23
高一学生王猛在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x?y|的值为(???)
A. 15 B. 16 C. 17 D. 18
某市教育局为了了解学生近视的情况,对四个非毕业年级各班的近视学生人数做了统计,每个年级都有10个班,如果某个年级的每个班的近视人数都不超过5人,则认定该年级为“学生视力保护达标年级”,这四个年级各班近视学生人数情况统计如下表:
初一年级????????????? 平均值为2,方差为2
初二年级????????????? 平均值为1,方差大于0
高一年级?????????????? 中位数为3,众数为4
高二年级?????????????? 平均值为3,中位数为4
从表中数据可知:一定是“学生视力保护达标年级”的是(??? )
A. 初一年级 B. 初二年级 C. 高一年级 D. 高二年级
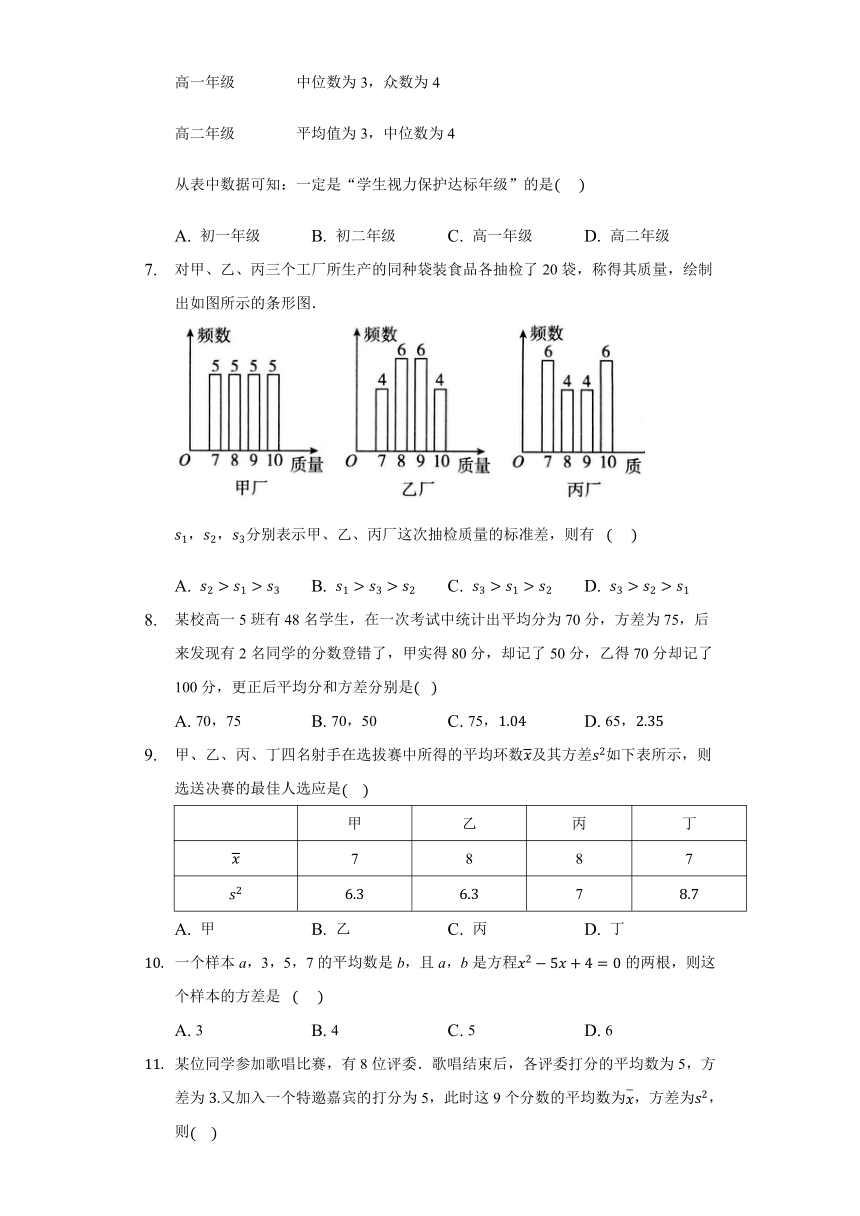
对甲、乙、丙三个工厂所生产的同种袋装食品各抽检了20袋,称得其质量,绘制出如图所示的条形图.
s1,s2,s3分别表示甲、乙、丙厂这次抽检质量的标准差,则有? (??? )
A. s2>s1>s3 B. s1>s3>s2 C. s3>s1>s2 D. s3>s2>s1
某校高一5班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的分数登错了,甲实得80分,却记了50分,乙得70分却记了100分,更正后平均分和方差分别是(? )
A. 70,75 B. 70,50 C. 75,1.04 D. 65,2.35
甲、乙、丙、丁四名射手在选拔赛中所得的平均环数x及其方差s2如下表所示,则选送决赛的最佳人选应是(????)
甲
乙
丙
丁
x
7
8
8
7
s2
6.3
6.3
7
8.7
A. 甲 B. 乙 C. 丙 D. 丁
一个样本a,3,5,7的平均数是b,且a,b是方程x2?5x+4=0的两根,则这个样本的方差是? (??? )
A. 3 B. 4 C. 5 D. 6
某位同学参加歌唱比赛,有8位评委.歌唱结束后,各评委打分的平均数为5,方差为3.又加入一个特邀嘉宾的打分为5,此时这9个分数的平均数为x?,方差为s2,则(????)
A. x?=5,s2>3 B. x?=5,s2<3
C. x?>5,s2<3 D. x?>5,s2>3
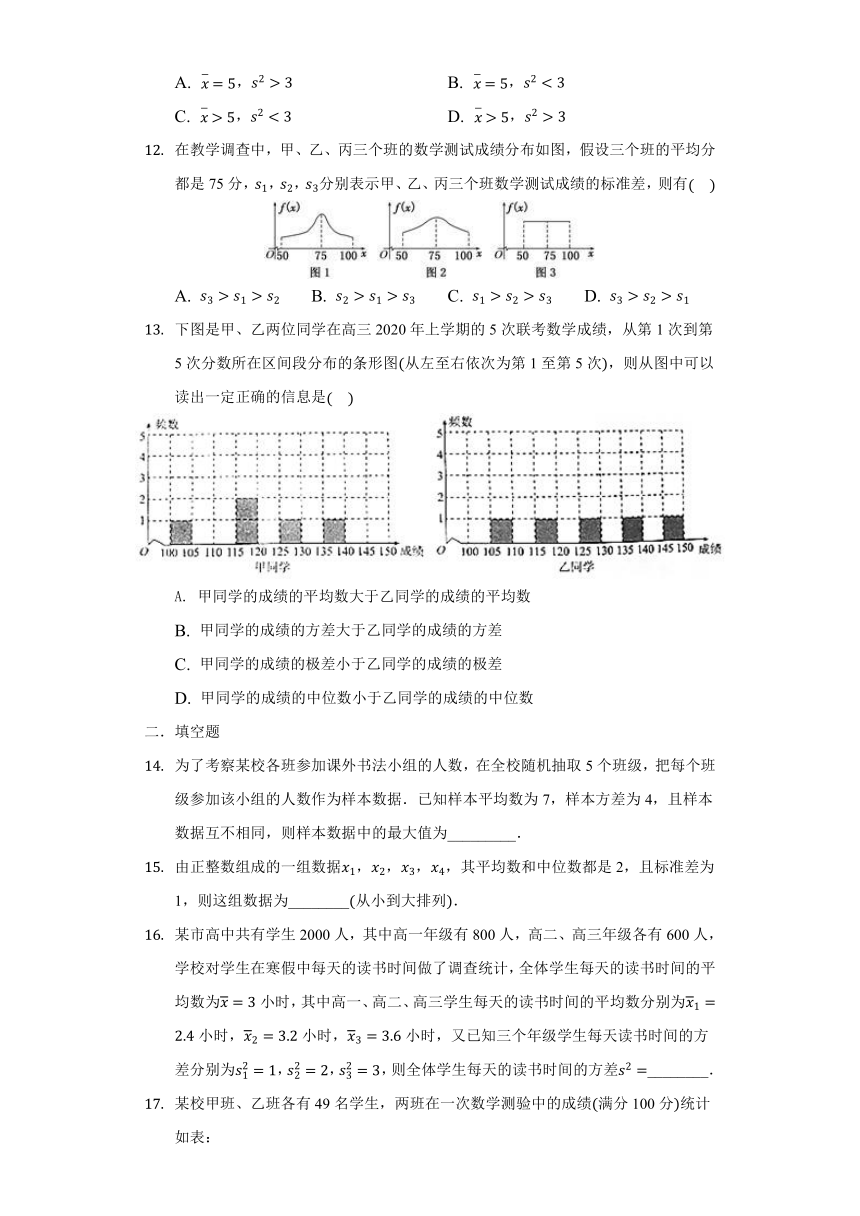
在教学调查中,甲、乙、丙三个班的数学测试成绩分布如图,假设三个班的平均分都是75分,s1,s2,s3分别表示甲、乙、丙三个班数学测试成绩的标准差,则有(????)
A. s3>s1>s2 B. s2>s1>s3 C. s1>s2>s3 D. s3>s2>s1
下图是甲、乙两位同学在高三2020年上学期的5次联考数学成绩,从第1次到第5次分数所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是(????)
甲同学的成绩的平均数大于乙同学的成绩的平均数
B. 甲同学的成绩的方差大于乙同学的成绩的方差
C. 甲同学的成绩的极差小于乙同学的成绩的极差
D. 甲同学的成绩的中位数小于乙同学的成绩的中位数
二.填空题
为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互不相同,则样本数据中的最大值为_________.
由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差为1,则这组数据为________(从小到大排列).
某市高中共有学生2000人,其中高一年级有800人,高二、高三年级各有600人,学校对学生在寒假中每天的读书时间做了调查统计,全体学生每天的读书时间的平均数为x=3小时,其中高一、高二、高三学生每天的读书时间的平均数分别为x1=2.4小时,x2=3.2小时,x3=3.6小时,又已知三个年级学生每天读书时间的方差分别为s12=1,s22=2,s32=3,则全体学生每天的读书时间的方差s2=________.
某校甲班、乙班各有49名学生,两班在一次数学测验中的成绩(满分100分)统计如表:
班级
平均分
众数
中位数
标准差
甲班
79
70
87
19.8
乙班
79
70
79
5.2
根据表格,对比甲、乙两班的成绩,对甲班提出的教学建议是??????????,对乙班提出的教学建议是??????????.
三.解答题
甲、乙二人参加某体育项目训练,近期的五次测试成绩如图所示.
(1)分别求出两人成绩的平均数与方差;
(2)根据统计图和(1)中算得的结果,对两人的训练成绩作出评价.
某学校餐厅有大米500袋,其中甲厂的产品有320袋,乙厂的产品有180袋.餐厅监管员为了得到这500袋大米的重量信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:kg),计算得出甲厂样本数据的平均数为100?kg,方差为20;乙厂样本数据的平均数是100?kg,方差是30.
(1)根据以上信息,能够计算出总的样本数据的平均数和方差吗?为什么?
(2)如果已知甲、乙两厂的样本量按比例分配,你能计算出总的样本数据的平均数和方差各为多少吗?
(3)如果已知甲、乙两厂的样本量都是30,你能计算出总的样本数据的平均数和方差各为多少吗?它们分别作为总体的平均数和方差的估计值合适吗?为什么?
某工厂36名工人的年龄数据如表.
工人编号? 年龄
工人编号? 年龄
工人编号? 年龄
工人编号? 年龄
1?40
10?36
19?27
28?34
2?44
11?31
20?43
29?39
3?40
12?38
21?41
30?43
4?41
13?39
22?37
31?38
5?33
14?43
23?34
32?42
6?40
15?45
24?42
33?53
7?45
16?39
25?37
34?37
8?42
17?38
26?44
35?49
9?43
18?36
27?42
36?39
采用随机抽样的方法抽出9名工人的年龄分别为44,40,36,43,36,37,44,43,37.
(1)计算抽出样本的均值x和方差s2;
(2)36名工人中年龄在x?s与x+s之间有多少人?所占的百分比是多少(精确到0.01%)?
答案和解析
1.【答案】B
【解析】
【分析】
本题给出五个数,通过已知情况求出平均数,并且进一步求它们的方差,着重考查了平均数和方差的计算公式,属于基础题.
根据题意,五个数据的平均数为10,然后可以用方差的计算公式,求出这五个数的方差,即可得到正确答案.
【解答】
解:∵五个数12,8,9,10,11的平均数为10,
所以五个数的方差为:s2=15[(12?10)2+(8?10)2+(9?10)2+(10?10)2+(11?10)2]=2
故答案为2,
故答案选B.
2.【答案】A
【解析】解:在某次测量中得到的A样本数据如下:22,23,25,26,31,30,
若B样本数据恰好是A样本数据每个数都减去10后所得的数据,
则A,B两样本的下列数字特征相同的是方差.
故选:A.
利用方差、平均数、众数、中位数的性质直接求解.
本题考查数字特征的判断,考查方差、平均数、众数、中位数的性质等基础知识,考查运算求解能力,是基础题.
3.【答案】A
【解析】
【分析】
根据方差的统计意义判断.方差越小数据越稳定.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【解答】
解:因为s甲2∴产量比较稳定的是甲.
故选A.
4.【答案】C
【解析】
【分析】
本题可将平均数和方差公式中的x换成3x?2,再化简进行计算.
本题考查的是方差和平均数的性质.
【解答】
解:∵x1,x2,…,x5的平均数是2,则x1+x2+…+x5=2×5=10.
∴数据3x1?2,3x2?2,3x3?2,3x4?2,3x5?2的平均数是:x?'=15[(3x1?2)+(3x2?2)+(3x3?2)+(3x4?2)+(3x5?2)]=15[3×(x1+x2+…+x5)?10]=4,
S'2=15×[(3x1?2?4)2+(3x2?2?4)2+…+(3x5?2?4)2],
=15×[(3x1?6)2+…+(3x5?6)2]=9×15[(x1?2)2+(x2?2)2+…+(x5?2)2]=3.
故选:C.
5.【答案】D
【解析】
【分析】根据平均数和方差的公式求解即可的结果.
【解答】
解:由题意得x+y+105+109+1105=108,①
(x?108)2+(y?108)2+9+1+45=35.2,②
由①②解得x=99,y=117或x=117,y=99,
所以|x?y|=18.
故选D.
6.【答案】A
【解析】
【分析】
本题考查了基本概念的掌握,需要学生掌握众数、中位数、平均数的优缺点,属于基础题.
根据平均值、方差、中位数以及众数的实际意义作出选择.
【解答】
解:能反应“学生视力保护达标年级”的是平均值和方差:
高一年级,知道中位数与众数,不能判断出是否达标,高二年级知道平均数与中位数,也不能判断是否达标;故排除CD;
初二年级,方差大于0,但不确定具体取值,因此初二年级也不能判断是否达标;
初一年级,平均数和方差均为2,满足题意,因为若有一个数据大于5,方差必然大于2.
故选:A.
7.【答案】C
【解析】
【分析】
本题考查数据的均值、方差、标准差,比较容易.分别计算三个厂的数据的均值、方差、标准差,再比较即可.
【解答】
解:根据题意,甲厂的平均数x1=120×(5×7+5×8+5×9+5×10)=8.5,
方差s12=120×5×(7?8.5)2+5×(8?8.5)2+5×(9?8.5)2+5×(10?8.5)2=1.25,标准差s1=1.25;?
乙厂的平均数x2=120×(4×7+6×8+6×9+4×10)=8.5,???
方差s22=120×4×(7?8.5)2+6×(8?8.5)2+6×(9?8.5)2+4×(10?8.5)2=1.05,标准差s2=1.05;??
? 丙厂的平均数x3=120×(6×7+4×8+4×9+6×10)=8.5,方差s32=120×6×(7?8.5)2+4×(8?8.5)2+4×(9?8.5)2+6×(10?8.5)2=1.45,标准差s3=1.45.???
所以s3>s1>s2.
故选C.
8.【答案】B
【解析】
【分析】
本题考查平均数和方差的计算,属于基础题.
因甲少记了30分,乙多记了30分,故平均分不变;设更正后的方差为s2,再根据方差公式,分别计算更正前后的方差,化简整理得到s2=50.
【解答】
解:因甲少记了30分,乙多记了30分,故平均分不变.
设更正后的方差为s2,
则由题意可得:s2=148[(x1?70)2+(x2?70)2+?+(80?70)2+(70?70)2+?+(x48?70)2],
而更正前有:75=148[(x1?70)2+(x2?70)2+?+(50?70)2+(100?70)2+?+?(x48?70)2],
化简整理得s2=50.
故选B.
9.【答案】B
【解析】
【分析】
本题考查了平均数和方差的有关知识,方差越小成绩越稳定.
【解答】
解:由题意得乙和丙的平均环数最大,但是乙的成绩更加稳定.故最佳人选是乙.
故选B.
10.【答案】C
【解析】
【分析】本题将解方程和求方差进行综合考查,解题时重点是要考虑a、b的取值情况.
先解方程求出a、b的值,然后根据方差的计算公式去求方差.方差s2=1n[(x1?x)2+(x2?x)2+?+(xn?x)2].
【解答】解:由根与系数的关系及平均数计算公式得a+b=5,a+3+5+7=4b,解得a=1,b=4,
则s2=14[(4?1)2+(4?3)2+(4?5)2+(4?7)2]=5.
11.【答案】B
【解析】解:x?=5,s2=19(02+8×3)=83<3.
故选:B.
由平均数和方差的性质得x?=5,s2=19(02+8×3)=83<3.
本题考查平均数、方差的求法,考查平均数、方差的性质等基础知识,考查运算求解能力,是基础题.
12.【答案】D
【解析】
【分析】
本题考查样本的数字特征,利用标准差的意义判断.属于基础题.
【解答】
解:所给图是成绩分布图,平均分是75分,
在图1中,集中在75分附近的数据最多,
图3中从50分到100分均匀分布,所有成绩不集中在任何一个数据附近,
图2介于两者之间.由标准差的意义可得s3>s2>s1.
故选D.
13.【答案】D
【解析】解:对于A,甲同学的平均成绩有一个100~105内的数,两个115~120内的数,没有145~150内的数,
他的成绩低于乙同学的平均数,A错误;
对于B,甲同学的成绩更集中些,他的成绩方差小于乙同学成绩的方差,B错误;
对于C,由频数分布表知甲的极差可以为140?110=40,乙的极差可以为145?110=35,
所以甲的极差也可能大于乙的极差,C错误;
对于D,甲同学的中位数在115~120,乙同学的中位数在125~130,
所以甲的中位数小于乙的中位数,D正确.
故选:D.
根据频数分布表中的数据,对选项中的命题进行分析,判断正误即可.
本题考查了频数分布与应用问题,是基础题.
14.【答案】10
【解析】设5个班级的人数分别为x1,x2,x3,x4,x5,则x1+x2+x3+x4+x55=7,
(x1?7)2+(x2?7)2+(x3?7)2+(x4?7)2+(x5?7)25
=4,
即5个整数平方和为20,最大的数比7大不能超过3,否则方差超过4,故最大值为10,最小值为4.
15.【答案】1,1,3,3
【解析】
【分析】本题考查中位数,平均数,标准差,解题的关键是利用相关公式建立方程,作了正确判断.由题意,可设x1≤x2≤x3≤x4,x1,x2,x3,x4∈N?,根据题设条件得出x1+x2+x3+x4=8,14x1?22+x2?22+x3?22+x4?22=1,再结合中位数是2,即可得出这组数据的值.
【解答】解:设x1≤x2≤x3≤x4,根据已知条件得到x1+x2+x3+x4=8,
且x2+x3=4,所以x1+x4=4,
又因为14x1?22+x2?22+x3?22+x4?22=1,
所以x1?2)2+x2?22=2,
又因为x1,x2,x3,x4是正整数,
所以x1?2)2=x2?22=1,
所以x1=1,x2=1,x3=3,x4=3.
16.【答案】2.164
【解析】
【分析】
本题考查方差的计算,属于基础题.
结合题意先计算各年级人数占全校的比率,再应用方差计算公式得到本题方差计算式直接计算即可.
【解答】
解:由题知:高一,高二,高三各年级学生人数占全效总数的比率依次为:8002000,6002000,6002000,
又因为全体学生每天的读书时间的平均数为x=3小时,
高一、高二、高三学生每天的读书时间的平均数分别为x1=2.4小时,x2=3.2小时,x3=3.6小时,
三个年级学生每天读书时间的方差分别为s12=1,s22=2,s32=3,
全体学生每天的读书时间的方差s2=8002000×[1+(2.4?3)2]+6002000×[2+(3.2?3)2]+6002000×[3+(3.6?3)2]=2.164.
故答案为2.164.
17.【答案】对学习有困难的同学多一些帮助??
采取措施提高优秀率
【解析】
【分析】
本题考查样本的数据特征,属于基础题.
利用已知数据,从中位数、平均分和标准差的角度可对甲、乙班提出建议.
【解答】
解:甲班学生成绩的中位数为87分.说明高于或等于87分的学生占一半以上,
而平均分为79分,标准差很大,说明低分也多,两极分化严重,建议对学习有困难的同学多给一些帮助;
乙班学生成绩的中位数和平均分均为79分,标准差小,说明学生成绩之间差别较小,成绩很差的学生少,
但成绩优异的学生也很少,建议采取措施提高优秀率.
故答案为对学习有困难的同学多一些帮助? ;采取措施提高优秀率.
18.【答案】解:(1)由题图可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.
?x甲=10+13+12+14+165=13,
?x乙=13+14+12+12+145=13,
?s甲2=15(10?13)2+(13?13)2+(12?13)2+(14?13)2+(16?13)2=4,
?s乙2=15(13?13)2+(14?13)2+(12?13)2+(12?13)2+(14?13)2=0.8.
(2)由s甲2>s乙2可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,
可知甲的成绩在不断提高,而乙的成绩则无明显提高.
【解析】本题主要考查平均数,方差的计算,以及折线图.属于基础题
(1)根据题目数据,利用平均数与方差的公式,即可得;
(2)根据(1)的结论,通过比较方差,即可得.
19.【答案】解:(1)根据题设条件可以得到甲、乙两厂样本数据的平均数都是100?kg,可以得到总的样本数据的平均数是100?kg,但是不能计算方差,因为本题中没有给出甲、乙两个厂的样本量,或者甲、乙样本量的比例,故无法计算出总的样本数据的方差;
(2)能;总的样本数据平均数为:320500×100+180500×100=100(kg),
总的样本数据方差为:320500×20+100?1002+180500×30+100?1002=23.6;
(3)能;总的样本数据的平均数为:3060×100+3060×100=100(kg),
总的样本数据的方差为:3060×20+100?1002+3060×30+100+1002=25,
甲、乙两厂样本数据的平均数都是100?kg,总的样本数据的平均数也为100?kg,?用100?kg作为总体的平均数合适,但用25作为总体的方差不合适,因为分层抽样中未按照比例抽样,总体中每个个体被抽到的可能性不完全相同,因而样本的代表性差.
【解析】本题考查用样本估计总体,属于拔高题.
(1)本题考查了分层抽样以及用样本估计总体,根据用样本估计总体的要求判断即可;
(2)本题考查了用样本估计总体,根据甲、乙两厂按比例抽取样本,再具体计算平均数和方差即可;
(3)本题考查了用样本估计总体,已知甲、乙两厂样本量,再具体计算平均数和方差,然后根据抽样分析中用样本估计总体每个个体被抽到的可能性相同判断即可。
20.【答案】解:(1)样本的平均值为x=44+40+36+43+36+37+44+43+379=40,
方差为:s2=19[(44?40)2+(40?40)2+(36?40)2+(43?40)2+(36?40)2+(37?40)2+?(44?40)2+(43?40)2+(37?40)2]
=19[42+02+(?4)2+32+(?4)2+(?3)2+42+32+(?3)2]=1009.
(2)由(1)知s=103,
所以x?s=1103,x+s=1303,
所以年龄在x?s与x+s之间的共有23人,所占的百分比为:2336×100%≈63.89%.
【解析】本题考查平均数、方差的计算,属于基础题.
(1)根据所给数据结合平均数、方差计算公式即可求得;
(2)由(1)中的平均值、方差可得x?s,x+s,即可得年龄在x?s与x+s之间的人数,从而可得所占的百分比.
学校:___________姓名:___________班级:___________学号:___________
一.选择题
小明5天上学途中所花的时间(单位:分钟)分别为12,8,10,9,11,则这组数据的方差为(? ? ? ?)
A. 4 B. 2 C. 9 D. 3
在某次测量中得到的A样本数据如下:22,23,25,26,31,30;若B样本数据恰好是A样本数据每个数都减
去10后所得的数据,则A,B两样本的下列数字特征相同的是(????)
A. 方差 B. 平均数 C. 众数 D. 中位数
某农科所种植的甲、乙两种水稻,连续六年在面积相等的两块稻田中作对比试验,试验得出平均产量是x甲=x乙=415㎏,方差是s甲2=794,s乙2=958,那么这两个水稻品种中产量比较稳定的是(????)
A. 甲 B. 乙
C. 甲、乙一样稳定 D. 无法确定
已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是13,那么另一组数3x1?2,3x2?2,3x3?2,3x4?2,3x5?2的平均数,方差分别是(????)
A. 2,13 B. 2,1 C. 4,3 D. 4,23
高一学生王猛在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x?y|的值为(???)
A. 15 B. 16 C. 17 D. 18
某市教育局为了了解学生近视的情况,对四个非毕业年级各班的近视学生人数做了统计,每个年级都有10个班,如果某个年级的每个班的近视人数都不超过5人,则认定该年级为“学生视力保护达标年级”,这四个年级各班近视学生人数情况统计如下表:
初一年级????????????? 平均值为2,方差为2
初二年级????????????? 平均值为1,方差大于0
高一年级?????????????? 中位数为3,众数为4
高二年级?????????????? 平均值为3,中位数为4
从表中数据可知:一定是“学生视力保护达标年级”的是(??? )
A. 初一年级 B. 初二年级 C. 高一年级 D. 高二年级
对甲、乙、丙三个工厂所生产的同种袋装食品各抽检了20袋,称得其质量,绘制出如图所示的条形图.
s1,s2,s3分别表示甲、乙、丙厂这次抽检质量的标准差,则有? (??? )
A. s2>s1>s3 B. s1>s3>s2 C. s3>s1>s2 D. s3>s2>s1
某校高一5班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的分数登错了,甲实得80分,却记了50分,乙得70分却记了100分,更正后平均分和方差分别是(? )
A. 70,75 B. 70,50 C. 75,1.04 D. 65,2.35
甲、乙、丙、丁四名射手在选拔赛中所得的平均环数x及其方差s2如下表所示,则选送决赛的最佳人选应是(????)
甲
乙
丙
丁
x
7
8
8
7
s2
6.3
6.3
7
8.7
A. 甲 B. 乙 C. 丙 D. 丁
一个样本a,3,5,7的平均数是b,且a,b是方程x2?5x+4=0的两根,则这个样本的方差是? (??? )
A. 3 B. 4 C. 5 D. 6
某位同学参加歌唱比赛,有8位评委.歌唱结束后,各评委打分的平均数为5,方差为3.又加入一个特邀嘉宾的打分为5,此时这9个分数的平均数为x?,方差为s2,则(????)
A. x?=5,s2>3 B. x?=5,s2<3
C. x?>5,s2<3 D. x?>5,s2>3
在教学调查中,甲、乙、丙三个班的数学测试成绩分布如图,假设三个班的平均分都是75分,s1,s2,s3分别表示甲、乙、丙三个班数学测试成绩的标准差,则有(????)
A. s3>s1>s2 B. s2>s1>s3 C. s1>s2>s3 D. s3>s2>s1
下图是甲、乙两位同学在高三2020年上学期的5次联考数学成绩,从第1次到第5次分数所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是(????)
甲同学的成绩的平均数大于乙同学的成绩的平均数
B. 甲同学的成绩的方差大于乙同学的成绩的方差
C. 甲同学的成绩的极差小于乙同学的成绩的极差
D. 甲同学的成绩的中位数小于乙同学的成绩的中位数
二.填空题
为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互不相同,则样本数据中的最大值为_________.
由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差为1,则这组数据为________(从小到大排列).
某市高中共有学生2000人,其中高一年级有800人,高二、高三年级各有600人,学校对学生在寒假中每天的读书时间做了调查统计,全体学生每天的读书时间的平均数为x=3小时,其中高一、高二、高三学生每天的读书时间的平均数分别为x1=2.4小时,x2=3.2小时,x3=3.6小时,又已知三个年级学生每天读书时间的方差分别为s12=1,s22=2,s32=3,则全体学生每天的读书时间的方差s2=________.
某校甲班、乙班各有49名学生,两班在一次数学测验中的成绩(满分100分)统计如表:
班级
平均分
众数
中位数
标准差
甲班
79
70
87
19.8
乙班
79
70
79
5.2
根据表格,对比甲、乙两班的成绩,对甲班提出的教学建议是??????????,对乙班提出的教学建议是??????????.
三.解答题
甲、乙二人参加某体育项目训练,近期的五次测试成绩如图所示.
(1)分别求出两人成绩的平均数与方差;
(2)根据统计图和(1)中算得的结果,对两人的训练成绩作出评价.
某学校餐厅有大米500袋,其中甲厂的产品有320袋,乙厂的产品有180袋.餐厅监管员为了得到这500袋大米的重量信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:kg),计算得出甲厂样本数据的平均数为100?kg,方差为20;乙厂样本数据的平均数是100?kg,方差是30.
(1)根据以上信息,能够计算出总的样本数据的平均数和方差吗?为什么?
(2)如果已知甲、乙两厂的样本量按比例分配,你能计算出总的样本数据的平均数和方差各为多少吗?
(3)如果已知甲、乙两厂的样本量都是30,你能计算出总的样本数据的平均数和方差各为多少吗?它们分别作为总体的平均数和方差的估计值合适吗?为什么?
某工厂36名工人的年龄数据如表.
工人编号? 年龄
工人编号? 年龄
工人编号? 年龄
工人编号? 年龄
1?40
10?36
19?27
28?34
2?44
11?31
20?43
29?39
3?40
12?38
21?41
30?43
4?41
13?39
22?37
31?38
5?33
14?43
23?34
32?42
6?40
15?45
24?42
33?53
7?45
16?39
25?37
34?37
8?42
17?38
26?44
35?49
9?43
18?36
27?42
36?39
采用随机抽样的方法抽出9名工人的年龄分别为44,40,36,43,36,37,44,43,37.
(1)计算抽出样本的均值x和方差s2;
(2)36名工人中年龄在x?s与x+s之间有多少人?所占的百分比是多少(精确到0.01%)?
答案和解析
1.【答案】B
【解析】
【分析】
本题给出五个数,通过已知情况求出平均数,并且进一步求它们的方差,着重考查了平均数和方差的计算公式,属于基础题.
根据题意,五个数据的平均数为10,然后可以用方差的计算公式,求出这五个数的方差,即可得到正确答案.
【解答】
解:∵五个数12,8,9,10,11的平均数为10,
所以五个数的方差为:s2=15[(12?10)2+(8?10)2+(9?10)2+(10?10)2+(11?10)2]=2
故答案为2,
故答案选B.
2.【答案】A
【解析】解:在某次测量中得到的A样本数据如下:22,23,25,26,31,30,
若B样本数据恰好是A样本数据每个数都减去10后所得的数据,
则A,B两样本的下列数字特征相同的是方差.
故选:A.
利用方差、平均数、众数、中位数的性质直接求解.
本题考查数字特征的判断,考查方差、平均数、众数、中位数的性质等基础知识,考查运算求解能力,是基础题.
3.【答案】A
【解析】
【分析】
根据方差的统计意义判断.方差越小数据越稳定.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【解答】
解:因为s甲2
故选A.
4.【答案】C
【解析】
【分析】
本题可将平均数和方差公式中的x换成3x?2,再化简进行计算.
本题考查的是方差和平均数的性质.
【解答】
解:∵x1,x2,…,x5的平均数是2,则x1+x2+…+x5=2×5=10.
∴数据3x1?2,3x2?2,3x3?2,3x4?2,3x5?2的平均数是:x?'=15[(3x1?2)+(3x2?2)+(3x3?2)+(3x4?2)+(3x5?2)]=15[3×(x1+x2+…+x5)?10]=4,
S'2=15×[(3x1?2?4)2+(3x2?2?4)2+…+(3x5?2?4)2],
=15×[(3x1?6)2+…+(3x5?6)2]=9×15[(x1?2)2+(x2?2)2+…+(x5?2)2]=3.
故选:C.
5.【答案】D
【解析】
【分析】根据平均数和方差的公式求解即可的结果.
【解答】
解:由题意得x+y+105+109+1105=108,①
(x?108)2+(y?108)2+9+1+45=35.2,②
由①②解得x=99,y=117或x=117,y=99,
所以|x?y|=18.
故选D.
6.【答案】A
【解析】
【分析】
本题考查了基本概念的掌握,需要学生掌握众数、中位数、平均数的优缺点,属于基础题.
根据平均值、方差、中位数以及众数的实际意义作出选择.
【解答】
解:能反应“学生视力保护达标年级”的是平均值和方差:
高一年级,知道中位数与众数,不能判断出是否达标,高二年级知道平均数与中位数,也不能判断是否达标;故排除CD;
初二年级,方差大于0,但不确定具体取值,因此初二年级也不能判断是否达标;
初一年级,平均数和方差均为2,满足题意,因为若有一个数据大于5,方差必然大于2.
故选:A.
7.【答案】C
【解析】
【分析】
本题考查数据的均值、方差、标准差,比较容易.分别计算三个厂的数据的均值、方差、标准差,再比较即可.
【解答】
解:根据题意,甲厂的平均数x1=120×(5×7+5×8+5×9+5×10)=8.5,
方差s12=120×5×(7?8.5)2+5×(8?8.5)2+5×(9?8.5)2+5×(10?8.5)2=1.25,标准差s1=1.25;?
乙厂的平均数x2=120×(4×7+6×8+6×9+4×10)=8.5,???
方差s22=120×4×(7?8.5)2+6×(8?8.5)2+6×(9?8.5)2+4×(10?8.5)2=1.05,标准差s2=1.05;??
? 丙厂的平均数x3=120×(6×7+4×8+4×9+6×10)=8.5,方差s32=120×6×(7?8.5)2+4×(8?8.5)2+4×(9?8.5)2+6×(10?8.5)2=1.45,标准差s3=1.45.???
所以s3>s1>s2.
故选C.
8.【答案】B
【解析】
【分析】
本题考查平均数和方差的计算,属于基础题.
因甲少记了30分,乙多记了30分,故平均分不变;设更正后的方差为s2,再根据方差公式,分别计算更正前后的方差,化简整理得到s2=50.
【解答】
解:因甲少记了30分,乙多记了30分,故平均分不变.
设更正后的方差为s2,
则由题意可得:s2=148[(x1?70)2+(x2?70)2+?+(80?70)2+(70?70)2+?+(x48?70)2],
而更正前有:75=148[(x1?70)2+(x2?70)2+?+(50?70)2+(100?70)2+?+?(x48?70)2],
化简整理得s2=50.
故选B.
9.【答案】B
【解析】
【分析】
本题考查了平均数和方差的有关知识,方差越小成绩越稳定.
【解答】
解:由题意得乙和丙的平均环数最大,但是乙的成绩更加稳定.故最佳人选是乙.
故选B.
10.【答案】C
【解析】
【分析】本题将解方程和求方差进行综合考查,解题时重点是要考虑a、b的取值情况.
先解方程求出a、b的值,然后根据方差的计算公式去求方差.方差s2=1n[(x1?x)2+(x2?x)2+?+(xn?x)2].
【解答】解:由根与系数的关系及平均数计算公式得a+b=5,a+3+5+7=4b,解得a=1,b=4,
则s2=14[(4?1)2+(4?3)2+(4?5)2+(4?7)2]=5.
11.【答案】B
【解析】解:x?=5,s2=19(02+8×3)=83<3.
故选:B.
由平均数和方差的性质得x?=5,s2=19(02+8×3)=83<3.
本题考查平均数、方差的求法,考查平均数、方差的性质等基础知识,考查运算求解能力,是基础题.
12.【答案】D
【解析】
【分析】
本题考查样本的数字特征,利用标准差的意义判断.属于基础题.
【解答】
解:所给图是成绩分布图,平均分是75分,
在图1中,集中在75分附近的数据最多,
图3中从50分到100分均匀分布,所有成绩不集中在任何一个数据附近,
图2介于两者之间.由标准差的意义可得s3>s2>s1.
故选D.
13.【答案】D
【解析】解:对于A,甲同学的平均成绩有一个100~105内的数,两个115~120内的数,没有145~150内的数,
他的成绩低于乙同学的平均数,A错误;
对于B,甲同学的成绩更集中些,他的成绩方差小于乙同学成绩的方差,B错误;
对于C,由频数分布表知甲的极差可以为140?110=40,乙的极差可以为145?110=35,
所以甲的极差也可能大于乙的极差,C错误;
对于D,甲同学的中位数在115~120,乙同学的中位数在125~130,
所以甲的中位数小于乙的中位数,D正确.
故选:D.
根据频数分布表中的数据,对选项中的命题进行分析,判断正误即可.
本题考查了频数分布与应用问题,是基础题.
14.【答案】10
【解析】设5个班级的人数分别为x1,x2,x3,x4,x5,则x1+x2+x3+x4+x55=7,
(x1?7)2+(x2?7)2+(x3?7)2+(x4?7)2+(x5?7)25
=4,
即5个整数平方和为20,最大的数比7大不能超过3,否则方差超过4,故最大值为10,最小值为4.
15.【答案】1,1,3,3
【解析】
【分析】本题考查中位数,平均数,标准差,解题的关键是利用相关公式建立方程,作了正确判断.由题意,可设x1≤x2≤x3≤x4,x1,x2,x3,x4∈N?,根据题设条件得出x1+x2+x3+x4=8,14x1?22+x2?22+x3?22+x4?22=1,再结合中位数是2,即可得出这组数据的值.
【解答】解:设x1≤x2≤x3≤x4,根据已知条件得到x1+x2+x3+x4=8,
且x2+x3=4,所以x1+x4=4,
又因为14x1?22+x2?22+x3?22+x4?22=1,
所以x1?2)2+x2?22=2,
又因为x1,x2,x3,x4是正整数,
所以x1?2)2=x2?22=1,
所以x1=1,x2=1,x3=3,x4=3.
16.【答案】2.164
【解析】
【分析】
本题考查方差的计算,属于基础题.
结合题意先计算各年级人数占全校的比率,再应用方差计算公式得到本题方差计算式直接计算即可.
【解答】
解:由题知:高一,高二,高三各年级学生人数占全效总数的比率依次为:8002000,6002000,6002000,
又因为全体学生每天的读书时间的平均数为x=3小时,
高一、高二、高三学生每天的读书时间的平均数分别为x1=2.4小时,x2=3.2小时,x3=3.6小时,
三个年级学生每天读书时间的方差分别为s12=1,s22=2,s32=3,
全体学生每天的读书时间的方差s2=8002000×[1+(2.4?3)2]+6002000×[2+(3.2?3)2]+6002000×[3+(3.6?3)2]=2.164.
故答案为2.164.
17.【答案】对学习有困难的同学多一些帮助??
采取措施提高优秀率
【解析】
【分析】
本题考查样本的数据特征,属于基础题.
利用已知数据,从中位数、平均分和标准差的角度可对甲、乙班提出建议.
【解答】
解:甲班学生成绩的中位数为87分.说明高于或等于87分的学生占一半以上,
而平均分为79分,标准差很大,说明低分也多,两极分化严重,建议对学习有困难的同学多给一些帮助;
乙班学生成绩的中位数和平均分均为79分,标准差小,说明学生成绩之间差别较小,成绩很差的学生少,
但成绩优异的学生也很少,建议采取措施提高优秀率.
故答案为对学习有困难的同学多一些帮助? ;采取措施提高优秀率.
18.【答案】解:(1)由题图可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.
?x甲=10+13+12+14+165=13,
?x乙=13+14+12+12+145=13,
?s甲2=15(10?13)2+(13?13)2+(12?13)2+(14?13)2+(16?13)2=4,
?s乙2=15(13?13)2+(14?13)2+(12?13)2+(12?13)2+(14?13)2=0.8.
(2)由s甲2>s乙2可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,
可知甲的成绩在不断提高,而乙的成绩则无明显提高.
【解析】本题主要考查平均数,方差的计算,以及折线图.属于基础题
(1)根据题目数据,利用平均数与方差的公式,即可得;
(2)根据(1)的结论,通过比较方差,即可得.
19.【答案】解:(1)根据题设条件可以得到甲、乙两厂样本数据的平均数都是100?kg,可以得到总的样本数据的平均数是100?kg,但是不能计算方差,因为本题中没有给出甲、乙两个厂的样本量,或者甲、乙样本量的比例,故无法计算出总的样本数据的方差;
(2)能;总的样本数据平均数为:320500×100+180500×100=100(kg),
总的样本数据方差为:320500×20+100?1002+180500×30+100?1002=23.6;
(3)能;总的样本数据的平均数为:3060×100+3060×100=100(kg),
总的样本数据的方差为:3060×20+100?1002+3060×30+100+1002=25,
甲、乙两厂样本数据的平均数都是100?kg,总的样本数据的平均数也为100?kg,?用100?kg作为总体的平均数合适,但用25作为总体的方差不合适,因为分层抽样中未按照比例抽样,总体中每个个体被抽到的可能性不完全相同,因而样本的代表性差.
【解析】本题考查用样本估计总体,属于拔高题.
(1)本题考查了分层抽样以及用样本估计总体,根据用样本估计总体的要求判断即可;
(2)本题考查了用样本估计总体,根据甲、乙两厂按比例抽取样本,再具体计算平均数和方差即可;
(3)本题考查了用样本估计总体,已知甲、乙两厂样本量,再具体计算平均数和方差,然后根据抽样分析中用样本估计总体每个个体被抽到的可能性相同判断即可。
20.【答案】解:(1)样本的平均值为x=44+40+36+43+36+37+44+43+379=40,
方差为:s2=19[(44?40)2+(40?40)2+(36?40)2+(43?40)2+(36?40)2+(37?40)2+?(44?40)2+(43?40)2+(37?40)2]
=19[42+02+(?4)2+32+(?4)2+(?3)2+42+32+(?3)2]=1009.
(2)由(1)知s=103,
所以x?s=1103,x+s=1303,
所以年龄在x?s与x+s之间的共有23人,所占的百分比为:2336×100%≈63.89%.
【解析】本题考查平均数、方差的计算,属于基础题.
(1)根据所给数据结合平均数、方差计算公式即可求得;
(2)由(1)中的平均值、方差可得x?s,x+s,即可得年龄在x?s与x+s之间的人数,从而可得所占的百分比.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
