8.6.2.2直线与平面垂直的性质-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(含解析)
文档属性
| 名称 | 8.6.2.2直线与平面垂直的性质-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 14:59:50 | ||
图片预览



文档简介
8.6.2.2 直线与平面垂直的性质-【新教材】人教A版(2019)高中数学必修第二册同步练习(含解析)
学校:___________姓名:___________班级:___________学号:___________
一.选择题
设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是(????)
A. 若m⊥α,n⊥α,则m//n
B. 若m//n,m//α,则n//α
C. 若m?α,n?β,则m,n是异面直线
D. 若α//β,m?α,n?β,则m//n
如图,在三棱锥P?ABC中,△ABC为直角三角形,∠ACB=90°,M为AB的中点,PM⊥平面ABC,直线l过点P,且直线l?//平面ABC,如果直线l到平面ABC的距离为d,那么(????)
A. PA=PB>PC=d
B. PA=PBC. PA=PB=PC>d
D. PA=PB=PC如图,在三棱锥P?ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,则下列结论不正确的是(????)
A. BC⊥平面PAB B. AD⊥PC
C. AD⊥平面PBC D. PB⊥平面ADC
如图,在直三棱柱ABC?A1B1C1中,AA1=4,AC=BC=2,∠ACB=90°,点D是A1B1的中点,F是侧面AA1B1B(含边界)上的动点.要使AB1⊥平面C1DF,则线段C1F的长的最大值为? (??? )
A. 5 B. 22
C. 13 D. 25
线段AB在平面α的同侧,A,B到α的距离分别为3和5,则AB的中点到α的距离为(????)
A. 4 B. 3 C. 2 D. 1
如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B,D,如果增加一个条件,就能推出BD⊥EF,则这个条件可能是(????)
A. AC⊥β B. AC⊥CD
C. AC//BD D. AC与α,β所成的角相等
如图所示,正方体ABCD?A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下说法中,正确的是? (??? )
A. 点H是△A1BD的垂心
B. AH垂直于平面CB1D1
C. AH的延长线经过点C1
D. 直线AH和BB1所成角为45°
如图所示,PA垂直于以AB为直径的圆O所在的平面,C为圆上异于A,B的任一点,则下列关系正确的是(????)
A. PA⊥BC B. BC⊥平面PAC
C. AC⊥PB D. PC⊥BC
如图所示,在正四棱锥(底面为正方形,顶点在底面的射影为底面的中心)S?ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为(????)
(1)EP⊥AC;(2)EP?//?BD;(3)EP?//平面SBD;(4)EP⊥平面SAC.
A. 1 B. 2 C. 3 D. 4
已知直线a,b和平面α,β,γ,可以使α//β的条件是(????)
A. a?α,b?β,a//b B. a?α,b?α,a//β,b//β
C. α⊥γ,β⊥γ D. a⊥α,a⊥β
地面上有两根相距a米的旗杆,它们的高分别是b米和c米(b>c),则它们上端的距离为(????)
a2+b2 B. b2+c2 C. a2+b2?c2 D. a2+(b?c)2
二.填空题
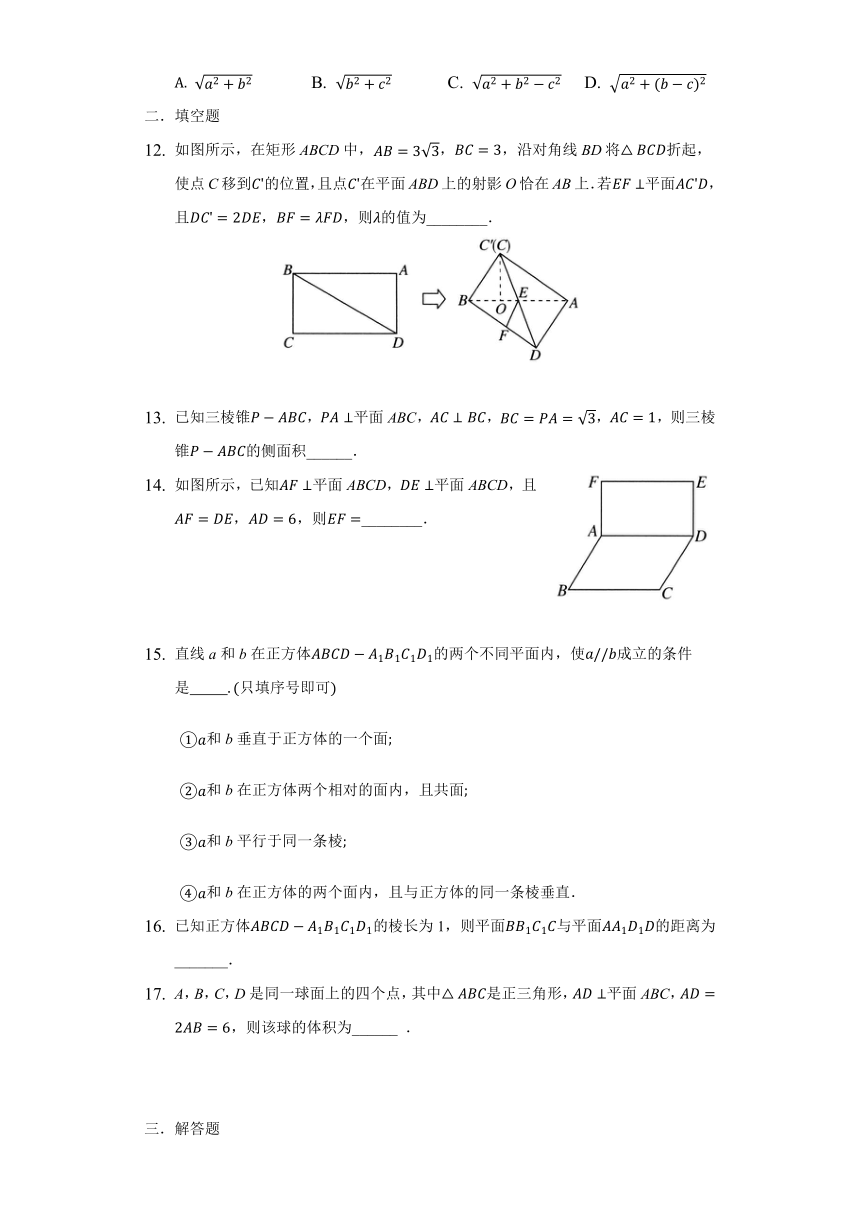
如图所示,在矩形ABCD中,AB=33,BC=3,沿对角线BD将△BCD折起,使点C移到C'的位置,且点C'在平面ABD上的射影O恰在AB上.若EF⊥平面AC'D,且DC'=2DE,BF=λFD,则λ的值为________.
已知三棱锥P?ABC,PA⊥平面ABC,AC⊥BC,BC=PA=3,AC=1,则三棱锥P?ABC的侧面积______.
如图所示,已知AF⊥平面ABCD,DE⊥平面ABCD,且AF=DE,AD=6,则EF=________.
直线a和b在正方体ABCD?A1B1C1D1的两个不同平面内,使a//b成立的条件是??????????.(只填序号即可)
?①a和b垂直于正方体的一个面;
?②a和b在正方体两个相对的面内,且共面;
?③a和b平行于同一条棱;
?④a和b在正方体的两个面内,且与正方体的同一条棱垂直.
已知正方体ABCD?A1B1C1D1的棱长为1,则平面BB1C1C与平面AA1D1D的距离为_______.
A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的体积为______ .
三.解答题
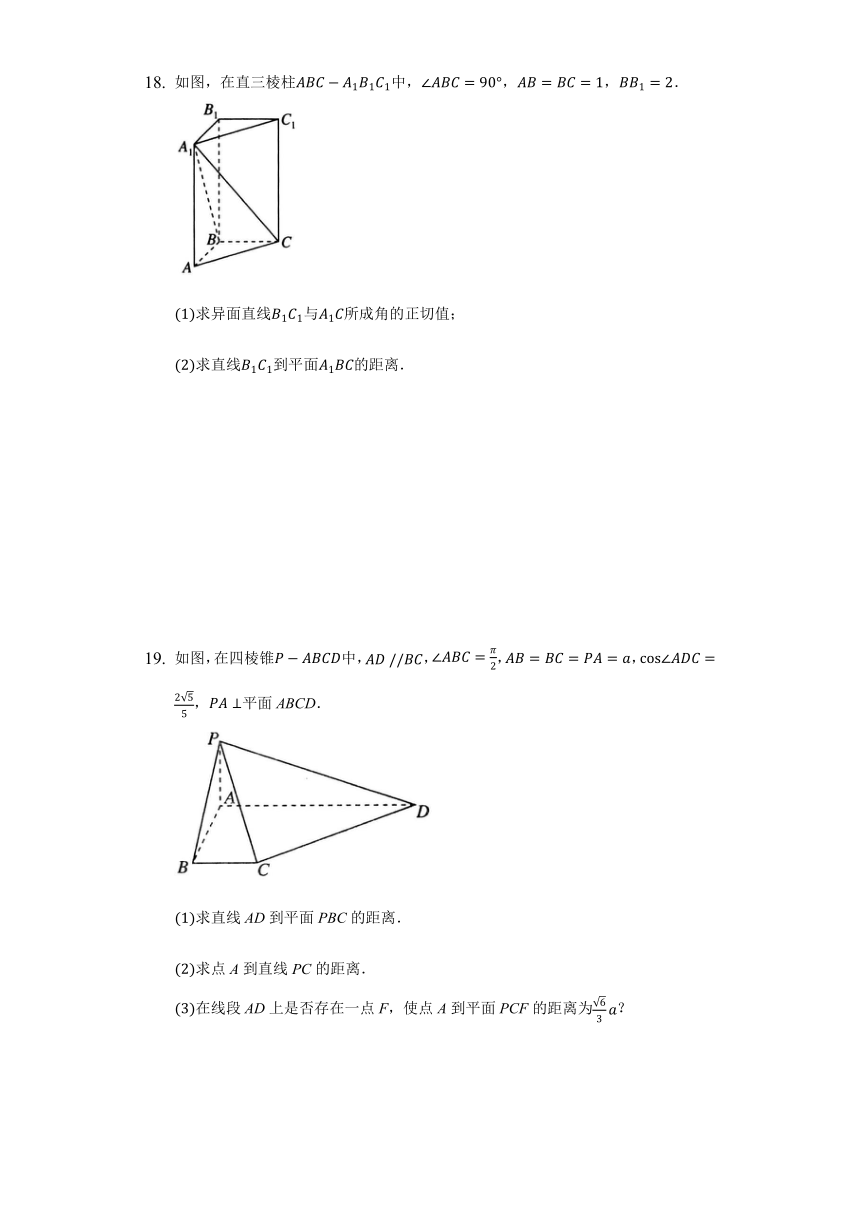
如图,在直三棱柱ABC?A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2.
(1)求异面直线B1C1与A1C所成角的正切值;
(2)求直线B1C1到平面A1BC的距离.
如图,在四棱锥P?ABCD中,AD?//BC,∠ABC=π2,AB=BC=PA=a,cos∠ADC=255,PA⊥平面ABCD.
(1)求直线AD到平面PBC的距离.
(2)求点A到直线PC的距离.
(3)在线段AD上是否存在一点F,使点A到平面PCF的距离为63a?
如图,四面体P?ABC中,PA⊥平面ABC,PA=1,AB=BC=1,AC=2.
(1)证明BC⊥平面PAB;
(2)在线段PC上是否存在点D,使得AC⊥BD,若存在,求PD的值,若不存在,请说明理由.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查空间中两直线的位置关系,线面平行的性质,面面平行的性质,属于基础题.
由空间中两直线的位置关系,线面平行的性质,面面平行的性质,逐个进行判断.
【解答】
解:对于A,垂直于同一个平面的两条直线互相平行,故A正确;
对于B,若m?//?n,m?//?α,则n?//?α或n?α,故B错误;
对于C,若m?α,n?β,则m,n的位置关系不确定,故C错误;
对于D,若α?//?β,m?α,n?β,则m,n的位置关系为平行或异面,故D错误.
故选A.
2.【答案】C
【解析】
【分析】
本题考查线面垂直的性质,属于基础题.
由线面垂直的性质得PM⊥MC,PM⊥AB,由M为AB的中点,得MA=MB=MC,则所以PA=PB=PC>d.
【解答】
解:由题意知d=PM.连接MC,
因为PM⊥平面ABC,AB,MC?平面ABC,
所以PM⊥MC,PM⊥AB.
因为M为AB的中点,∠ACB=90°,
所以MA=MB=MC,
所以PA=PB=PC>d.
故选C.
3.【答案】D
【解析】
【分析】
本题考查线面垂直的判定定理以及线面垂直的性质是应用,属于基础题.
由线面垂直的判定定理以及线面垂直的性质逐个进行判断.
【解答】
解:∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
又AB⊥BC,PA∩AB=A,
PA?面PAB,AB?面PAB
∴BC⊥平面PAB,故A中结论正确;
由BC⊥平面PAB,AD?平面PAB,得BC⊥AD,
∵PA=AB,D为PB的中点,
∴AD⊥PB,又PB∩BC=B,
PB?面PBC,BC?面PBC
∴AD⊥平面PBC,
又PC?平面PBC,
∴AD⊥PC,故B,C中结论正确;
在平面PBC中,∵PB⊥BC,∴PB与CD不垂直,故PB不垂直平面ADC,故D中结论错误.
故选D.
4.【答案】A
【解析】
【分析】
本题考查线面垂直,考查空间想象能力,属于中档题.
作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点F即为所求,由C1D⊥平面AA1BB,AB1?平面AA1B1B,则C1D⊥AB1,AB1⊥DF,DF∩C1D=D,满足线面垂直的判定定理,则AB1⊥平面C1DF.
【解答】
解:作DE⊥AB1交AB1于E,延长DE交BB1于F,
连接C1F,则AB1⊥平面C1DF,点F即为所求.
若AB1⊥平面C1DF,则AB1⊥DF,
故F在边界BB1上时,C1F的长取到最大值,
此时因为AB1⊥DF,
故∠FDB1+∠AB1A1=∠B1AA1+∠AB1A1=90°,
故∠FDB1=∠B1AA1,
故tan∠FDB1=tan∠B1AA1,即FB1DB1=A1B1AA1,
故FB1=A1B1?DB1AA1=22+22×22+2224=1此时C1F=FB12+C1B12=1+4=5,
故选A.
5.【答案】A
【解析】
【分析】本题考查空间中的距离.因为A,B两点在α同侧,根据中点坐标公式求解.
【解答】如图,设AB的中点为M,分别过A,M,B向α作垂线,垂足分别为A1,M1,B1,则由线面垂直的性质定理可知AA1?//?MM1?//?BB1.结合题意知,四边形AA1B1B为直角梯形,AA1=3,BB1=5,MM1为其中位线,∴MM1=4.故选A.
6.【答案】A
【解析】
【分析】
本题考查空间直线和直线垂直的判定,考查线面垂直的判定与性质,属于中档题,A条件加入,可判断出AC与EF垂直,这样EF和平面ABDC内两条相交线垂直,得到EF与平面ABDC垂直的结论,从而证出结论,条件BC只能得到ABDC为矩形,得不到所要结论,条件D而举反例说明错误.
【解答】
解:AB⊥α,CD⊥α,则AB和CD平行,AB和CD确定平面为平面ABDC,
增加条件A,由AB⊥α,CD⊥α,EF?α,得AB⊥EF,
AC⊥β,EF在平面β内,故 AC⊥EF,则EF与平面ABDC内两条相交直线AC,AB都垂直,
由线面垂直的判这定定理,EF⊥平面ABDC,BD在平面ABDC内,?
所以BD⊥EF,A正确;
增加条件B,C只能得到ABDC为矩形的结论,BD和EF同在平面α内,
BD和EF平行,相交或重合的可能性都有,也包括垂直,
BD⊥EF不一定成立,故 B,C错误;
不妨设ABCD是一个矩形,且BD和EF平行,此时AC和BD平行,
AC与EF与平行,AC与两平面α,β成等角,但BD⊥EF不成立,故D错误,
故选A.
7.【答案】ABC
【解析】
【分析】
本题考查面面平行的判定与性质,线面垂直的判定,涉及正方体的结构特征,属基础题.
根据AB=AA1=AD,可以得到A到△A1BD各顶点的距离相等,可得A正确;利用面面平行的判定定理平面CB1D1//平面A1BD,于是得到AH⊥平面CB1D1,判定B;连接AC1,利用线面垂直的判定定理可得AC1⊥平面A1BD,从而判定C;利用异面直线所成角的定义可得直线AH和BB1所成角为∠A1AC1,判定不是45°,从而判定D.
【解答】
解:∵△A1BD为等边三角形,∴其四心合一,
又∵AB=AA1=AD,
∴A到△A1BD各顶点的距离相等,∴A正确.
∵CD1//BA1,CB1//DA1,CD1∩CB1=C,BA1∩DA1=A1,
CD1、CB1?平面CB1D1,BA1、DA1?平面A1BD,
∴平面CB1D1//平面A1BD,
∴AH⊥平面CB1D1,∴B正确.
连接AC1,则AC1⊥BD,AC1⊥BA1,又BD∩BA1=B,
BD、BA1?平面A1BD,
∴AC1⊥平面A1BD,∴A,H,C1三点共线,
∴C正确.
∵直线AH和BB1所成角为∠A1AC1,而AA1≠A1C1,∴∠A1AC1≠45°,故D错误,
故选ABC.
8.【答案】ABD
【解析】
【分析】
本题考查线面垂直的判定与性质,属于基础题.
根据线面垂直的判定与性质逐项判断,即可得到答案.
【解答】
解:由PA⊥平面ABC,BC?平面ABC,
得PA⊥BC,所以A正确;
又BC⊥AC,PA∩AC=A,PA,AC?平面PAC,
∴BC⊥平面PAC,
又PC?平面PAC,
∴BC⊥PC,所以B,D均正确.
若AC⊥PB,又因为BC⊥AC,PB∩BC=B,PB,BC?平面PBC,
所以AC⊥平面PBC,
又PC?平面PBC,
则AC⊥PC,
又PA⊥平面ABC,AC?平面ABC,则PA⊥AC,产生矛盾,故C不正确.
故选ABD.
9.【答案】B
【解析】
【分析】
本题考查线线、线面、面面的位置关系及线面平行、线面垂直的判定定理.
连接AC、BD相交于点O,连接EM,EN,SO.(1)先证明AC⊥平面SBD,再利用三角形的中位线可得EM//BD,MN//SD,于是平面EMN//平面SBD,进而得到AC⊥平面EMN,AC⊥EP;(2)当点P与点M不重合时,由异面直线的定义可知:EP与BD是异面直线,因此不可能EP//BD;(3)由(1)可知:平面EMN//平面SBD,可得EP//平面SBD;(4)由(1)同理可得:EM⊥平面SAC,可用反证法证明:当P与M不重合时,EP与平面SAC不垂直.
【解答】
解:如图所示,连接AC、BD相交于点O,连接EM,EN,SO.
(1)由正四棱锥S?ABCD,可得SO⊥底面ABCD,AC⊥BD,
又AC?底面ABCD,
∴SO⊥AC.
∵SO∩BD=O,SO、BD?平面SBD,
∴AC⊥平面SBD,
∵E,M,N分别是BC,CD,SC的中点,
∴EM//BD,MN//SD,
∵MN,EM?平面SBD,SD,BD?平面SBD,
∴EM//平面SBD,MN//平面SBD,
而EM∩MN=M,EM、MN?平面EMN,
∴平面EMN//平面SBD,∴AC⊥平面EMN,
又EP?平面EMN,
∴AC⊥EP.故正确.
(2)当点P与点M重合时,有EP//BD;
当点P与点M不重合时,由异面直线的定义可知:EP与BD是异面直线,不可能EP//BD,
因此EP//BD不恒成立;
(3)由(1)可知:平面EMN//平面SBD,又EP?平面EMN,∴EP//平面SBD,因此正确.
(4)由(1)可得:SO⊥底面ABCD,又BD?底面ABCD,∴SO⊥BD.
又AC⊥BD,AC∩SO=O,SO、AC?平面SAC,
∴BD⊥平面SAC,又EM//BD,∴EM⊥平面SAC,
当点P与点M重合时,满足EP⊥面SAC;
当点P与点M不重合时,
若EP⊥平面SAC,则EP//EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.
因此EP⊥面SAC不恒成立.
综上可知:只有(1)(3)正确.即四个结论中恒成立的个数是2.
故选:B.
10.【答案】D
【解析】
【分析】
本题考查空间两平面平行的判定,属于基础题.
根据两平面平行的判定定理和推论,可得结论.
【解答】
解:两条平行直线分别在两个平面内,这两个平面有可能相交,排除A;
一个平面的两条直线都平行于另一个平面,这两个平面有可能相交,排除B;
两个平面都垂直于同一个平面,这两个平面有可能相交,排除C;
垂直于同一条直线的两个平面平行,D正确。
故选D
11.【答案】D
【解析】
【分析】
本题考查空间距离有计算,涉及线面垂直的性质的应用,属于基础题.
由已知两根旗杆所在的直线平行,由已知构造直角三角形求解即可.
【解答】
解:设AB,CD分别为两根旗杆所在的线段,
如图,由线面垂直的性质定理可知AB?//?CD,作AE⊥CD于E,则DE=b?c,
故AD=a2+(b?c)2.
故选D.
12.【答案】1
【解析】
【分析】
本题主要考查了线面垂直的判定,注意空间思维能力的培养.
证明BC'⊥平面AC'D,结合EF⊥平面AC'D,由线面垂直的性质得到EF?//?BC',即可求得λ的值.
【解答】
解:∵点C'在平面ABD上的射影O在AB上,∴C'O⊥平面ABD.
∵DA?平面ABD,∴C'O⊥DA.又∵AD⊥AB,AB∩C'O=O,
∴DA⊥平面ABC'.
又BC'?平面ABC',∴DA⊥BC'.
又∵BC'⊥C'D,DA∩C'D=D,∴BC'⊥平面AC'D.
又∵EF⊥平面AC'D,∴EF?//?BC'.∵DC'=2DE,即E为C'D的中点,∴F为BD的中点,
∴BF=FD,即λ=1.
13.【答案】532
【解析】解:如图所示,
三棱锥P?ABC中,PA⊥平面ABC,
∴PA⊥AB,PA⊥AC,PA⊥BC;
又AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥PC;
∴三棱锥P?ABC的各个面都是直角三角形;
又BC=PA=3,AC=1,
∴三棱锥P?ABC的侧面积为
S侧面积=S△PAB+S△PAC+S△PBC
=12×3×(3)2+12+12×3×1+12×3×(3)2+12
=532.
故答案为:532.
根据题意画出图形,证明三棱锥P?ABC的各个面都是直角三角形,再求三棱锥的侧面面积.
本题考查了三棱锥的结构特征与空间中的垂直关系应用问题,是基础题.
14.【答案】6
【解析】
【分析】
本题考查的是直线与平面垂直关系的应用,解题的关键是熟练掌握直线与平面垂直的性质;经审题,根据直线和平面垂直的性质定理知AF//DE,结合已知条件可判断出四边形AFED的形状;四边形AFED为平行四边形,根据平行四边形的性质即可得到本题答案.
【解答】
解:∵AF⊥平面ABCD,DE⊥平面ABCD,∴AF//DE,又∵AF=DE,∴四边形AFED是平行四边形,
∴EF=AD=6,
故答案为6.
15.【答案】?①?②?③
【解析】
【分析】
本题考查线面垂直的性质定理、面面平行的性质定理、平行公理以及空间两条直线的位置关系,属于基础题.
对于?①,利用线面垂直的性质即可判断为正确;
对于?②,利用面面平行的性质即可判断为正确;
对于?③,应用平行公理即可判断为正确;
对于?④,a,b可能平行、异面和垂直三种情况,?④错误.
【解答】
解:对于?①,利用线面垂直的性质可知?①正确;对于?②,由于a,b共面,利用面面平行的性质即可判断a//b,故?②正确;对于?③,应用平行公理可知?③正确;对于?④,当a和b在正方体的两个平行面内,且与正方体的同一条棱垂直时,a,b可能平行、异面和垂直三种情况,故?④错误.
故答案为:?①?②?③
16.【答案】1
【解析】
【分析】
本题考查平面到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
根据正方体的结构特征可知AB⊥平面BB1C1C,且AB⊥平面AA1D1D,即可得知棱AB的长即为所求.
【解答】
解:因为正方体的对面互相平行,
AB⊥平面BB1C1C,且AB⊥平面AA1D1D,
所以棱AB的长即为平面BB1C1C与平面AA1D1D的距离,且距离为1.
故答案为:1.
17.【答案】323π
【解析】
【分析】
本题考查球内接多面体,考查球的体积,考查学生的计算能力,比较基础.
由题意把A、B、C、D扩展为三棱柱如图,求出上下底面中心连线的中点与A的距离为球的半径,然后求出球的体积.
【解答】
解:由题意画出几何体的图形如图,
把A、B、C、D扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
AD=2AB=6,OE=3,△ABC是正三角形,
所以AE=23AB2?(12AB)2=3.
R=AO=32+3=23,可得球的体积为4πR33=323π.
故答案为:323π.
18.【答案】解:(1)由题意可得BC//B1C1,
∴∠A1CB(或其补角)即为异面直线B1C1与A1C所成的角,
由题意可知BB1⊥平面ABC,BC?平面ABC,
∴BB1⊥BC,
又AB⊥BC,AB∩BB1=B,AB?平面ABB1A1,BB1?平面ABB1A1,
∴BC⊥平面ABB1A1,
∵A1B?平面ABB1A1,∴BC⊥A1B,
∴△A1BC为直角三角形,
∴tan∠A1CB=A1BBC=AB2+BB12BC=5,
∴异面直线B1C1与A1C所成的角的正切值为5;
(2)∵BC//B1C1,BC?平面A1BC,B1C1?平面A1BC,
∴B1C1//平面A1BC,
∴直线B1C1上任意一点到平面A1BC的距离均为直线B1C1到平面A1BC的距离,
不妨取B1,且设B1到平面A1BC的距离为h,
由等体积法可得VB1?A1BC=VC?A1BB1,即13S△A1BC×?=13S△ABB1×BC,
代入数据可得13×12×1×5×?=13×12×2×1×1,解得?=255,
∴直线B1C1到平面A1BC的距离为255.
【解析】本题考查异面直线所成的角,涉及直线到平面的距离,等体积是解决问题的关键,属中档题.
(1)由题意可得∠A1CB(或其补角)即为异面直线B1C1与A1C所成的角,解三角形可得;
(2)可证B1C1//平面A1BC,则B1到平面A1BC的距离h即为所求,由等体积法可得VB1?A1BC=VC?A1BB1,代入数据计算可得.
19.【答案】解:(1)∵AD?//?BC,AD?平面PBC,BC?平面PBC,
∴AD?//平面PBC,
∴AD到平面PBC的距离等于点A到平面PBC的距离,
过点A作AH⊥PB,交PB于H,如图所示,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵BC⊥AB,PA∩AB=A,PA,AB?平面PAB,
∴BC⊥平面PAB,?
又AH?平面PAB,
∴BC⊥AH,?
又AH⊥PB,PB∩BC=B,PB,BC?平面PBC,
∴AH⊥平面PBC,
∴AH的长即为点A到平面PBC的距离,也即直线AD到平面PBC的距离,
在等腰直角三角形PAB中,易得AH=22a,
所以直线AD到平面PBC的距离为22a.
(2)过点A作AE⊥PC,交PC于E,则AE的长即为点A到PC的距离.连接AC,
在Rt△PAC中,PA=a,AC=2a,PC=3a,
∵AE·PC=PA·AC,
∴AE=PA?ACPC=63a,即点A到直线PC的距离为63a.
(3)假设在线段AD上存在一点F,使点A到平面PCF的距离为63a,
过点C作CM⊥AD,交AD于M,
在Rt△CMD中,CM=a,cos∠MDC=255,可得CD=5a,DM=2a,
所以AD=3a.? 由(2)知AE=63a,
若存在满足题意的F,则只需AE⊥平面PCF,
由条件可知,只需AC⊥CF,
设DF=x,则AF=3a?x,?
在△CDF中,由余弦定理可得CF2=x2+5a2?4ax,
若AC⊥CF,则在Rt△ACF中,AF2=CF2+AC2,?
即(3a?x)2=2a2+x2+5a2?4ax,解得x=a,?
即在AD上存在一点F,当AF=2a时,AC⊥CF,
又PA⊥CF,PA∩AC=A,
∴CF⊥平面PAC,
∴CF⊥AE,又AE⊥PC,PC∩CF=C,
∴AE⊥平面PCF,即点A到平面PCF的距离为AE=63a.
【解析】本题主要考查空间距离,属于中档题.
(1)由线面垂直的判断得AH⊥平面PBC,在三角形中求AH,得答案;
(2)过点A作AE⊥PC,交PC于E,则AE的长即为点A到PC的距离.在Rt△PAC中,由AE·PC=PA·AC,求解AE得答案;
(3)假设在线段AD上存在一点F,使点A到平面PCF的距离为63a,过点C作CM⊥AD,交AD于M,若存在满足题意的F,则只需AE⊥平面PCF,由线面垂直得点A到平面PCF的距离.
20.【答案】证明:(1)由题设知AB=BC=1,AC=2,
∴AB2+BC2=AC2,∴AB⊥BC,
∵PA⊥平面ABC,∴PA⊥BC,PA⊥AB,
∵PA∩AB=A,∴BC⊥平面PAB.
解:(2)点D为PC的中点,且PD=32,使得AC⊥BD.
理由如下:
在平面ABC内,过点B作BE⊥AC,垂足为E,
在平面PAC内,过点E作DE//PA,交PC于点D,连结BD,
由PA⊥平面ABC,知PA⊥AC,∴DE⊥AC,
∴AC⊥平面DBE,
∵BD?平面DBE,∴AC⊥BD,
在△ABC中,AB=BC=1,点E为AC的中点,则点D为PC的中点,
在Rt△APC中,AP=1,AC=2,∴PC=3,
∴PD=32.
【解析】(1)推导出AB⊥BC,PA⊥BC,PA⊥AB,由此能证明BC⊥平面PAB.
(2)过点B作BE⊥AC,垂足为E,过点E作DE//PA,交PC于点D,连结BD,推导出PA⊥AC,DE⊥AC,从而AC⊥平面DBE,进而AC⊥BD,由此能求出点D为PC的中点,且PD=32,使得AC⊥BD.
本题考查线面垂直的证明,考查满足线线垂直的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
学校:___________姓名:___________班级:___________学号:___________
一.选择题
设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是(????)
A. 若m⊥α,n⊥α,则m//n
B. 若m//n,m//α,则n//α
C. 若m?α,n?β,则m,n是异面直线
D. 若α//β,m?α,n?β,则m//n
如图,在三棱锥P?ABC中,△ABC为直角三角形,∠ACB=90°,M为AB的中点,PM⊥平面ABC,直线l过点P,且直线l?//平面ABC,如果直线l到平面ABC的距离为d,那么(????)
A. PA=PB>PC=d
B. PA=PB
D. PA=PB=PC
A. BC⊥平面PAB B. AD⊥PC
C. AD⊥平面PBC D. PB⊥平面ADC
如图,在直三棱柱ABC?A1B1C1中,AA1=4,AC=BC=2,∠ACB=90°,点D是A1B1的中点,F是侧面AA1B1B(含边界)上的动点.要使AB1⊥平面C1DF,则线段C1F的长的最大值为? (??? )
A. 5 B. 22
C. 13 D. 25
线段AB在平面α的同侧,A,B到α的距离分别为3和5,则AB的中点到α的距离为(????)
A. 4 B. 3 C. 2 D. 1
如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B,D,如果增加一个条件,就能推出BD⊥EF,则这个条件可能是(????)
A. AC⊥β B. AC⊥CD
C. AC//BD D. AC与α,β所成的角相等
如图所示,正方体ABCD?A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下说法中,正确的是? (??? )
A. 点H是△A1BD的垂心
B. AH垂直于平面CB1D1
C. AH的延长线经过点C1
D. 直线AH和BB1所成角为45°
如图所示,PA垂直于以AB为直径的圆O所在的平面,C为圆上异于A,B的任一点,则下列关系正确的是(????)
A. PA⊥BC B. BC⊥平面PAC
C. AC⊥PB D. PC⊥BC
如图所示,在正四棱锥(底面为正方形,顶点在底面的射影为底面的中心)S?ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为(????)
(1)EP⊥AC;(2)EP?//?BD;(3)EP?//平面SBD;(4)EP⊥平面SAC.
A. 1 B. 2 C. 3 D. 4
已知直线a,b和平面α,β,γ,可以使α//β的条件是(????)
A. a?α,b?β,a//b B. a?α,b?α,a//β,b//β
C. α⊥γ,β⊥γ D. a⊥α,a⊥β
地面上有两根相距a米的旗杆,它们的高分别是b米和c米(b>c),则它们上端的距离为(????)
a2+b2 B. b2+c2 C. a2+b2?c2 D. a2+(b?c)2
二.填空题
如图所示,在矩形ABCD中,AB=33,BC=3,沿对角线BD将△BCD折起,使点C移到C'的位置,且点C'在平面ABD上的射影O恰在AB上.若EF⊥平面AC'D,且DC'=2DE,BF=λFD,则λ的值为________.
已知三棱锥P?ABC,PA⊥平面ABC,AC⊥BC,BC=PA=3,AC=1,则三棱锥P?ABC的侧面积______.
如图所示,已知AF⊥平面ABCD,DE⊥平面ABCD,且AF=DE,AD=6,则EF=________.
直线a和b在正方体ABCD?A1B1C1D1的两个不同平面内,使a//b成立的条件是??????????.(只填序号即可)
?①a和b垂直于正方体的一个面;
?②a和b在正方体两个相对的面内,且共面;
?③a和b平行于同一条棱;
?④a和b在正方体的两个面内,且与正方体的同一条棱垂直.
已知正方体ABCD?A1B1C1D1的棱长为1,则平面BB1C1C与平面AA1D1D的距离为_______.
A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的体积为______ .
三.解答题
如图,在直三棱柱ABC?A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2.
(1)求异面直线B1C1与A1C所成角的正切值;
(2)求直线B1C1到平面A1BC的距离.
如图,在四棱锥P?ABCD中,AD?//BC,∠ABC=π2,AB=BC=PA=a,cos∠ADC=255,PA⊥平面ABCD.
(1)求直线AD到平面PBC的距离.
(2)求点A到直线PC的距离.
(3)在线段AD上是否存在一点F,使点A到平面PCF的距离为63a?
如图,四面体P?ABC中,PA⊥平面ABC,PA=1,AB=BC=1,AC=2.
(1)证明BC⊥平面PAB;
(2)在线段PC上是否存在点D,使得AC⊥BD,若存在,求PD的值,若不存在,请说明理由.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查空间中两直线的位置关系,线面平行的性质,面面平行的性质,属于基础题.
由空间中两直线的位置关系,线面平行的性质,面面平行的性质,逐个进行判断.
【解答】
解:对于A,垂直于同一个平面的两条直线互相平行,故A正确;
对于B,若m?//?n,m?//?α,则n?//?α或n?α,故B错误;
对于C,若m?α,n?β,则m,n的位置关系不确定,故C错误;
对于D,若α?//?β,m?α,n?β,则m,n的位置关系为平行或异面,故D错误.
故选A.
2.【答案】C
【解析】
【分析】
本题考查线面垂直的性质,属于基础题.
由线面垂直的性质得PM⊥MC,PM⊥AB,由M为AB的中点,得MA=MB=MC,则所以PA=PB=PC>d.
【解答】
解:由题意知d=PM.连接MC,
因为PM⊥平面ABC,AB,MC?平面ABC,
所以PM⊥MC,PM⊥AB.
因为M为AB的中点,∠ACB=90°,
所以MA=MB=MC,
所以PA=PB=PC>d.
故选C.
3.【答案】D
【解析】
【分析】
本题考查线面垂直的判定定理以及线面垂直的性质是应用,属于基础题.
由线面垂直的判定定理以及线面垂直的性质逐个进行判断.
【解答】
解:∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
又AB⊥BC,PA∩AB=A,
PA?面PAB,AB?面PAB
∴BC⊥平面PAB,故A中结论正确;
由BC⊥平面PAB,AD?平面PAB,得BC⊥AD,
∵PA=AB,D为PB的中点,
∴AD⊥PB,又PB∩BC=B,
PB?面PBC,BC?面PBC
∴AD⊥平面PBC,
又PC?平面PBC,
∴AD⊥PC,故B,C中结论正确;
在平面PBC中,∵PB⊥BC,∴PB与CD不垂直,故PB不垂直平面ADC,故D中结论错误.
故选D.
4.【答案】A
【解析】
【分析】
本题考查线面垂直,考查空间想象能力,属于中档题.
作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点F即为所求,由C1D⊥平面AA1BB,AB1?平面AA1B1B,则C1D⊥AB1,AB1⊥DF,DF∩C1D=D,满足线面垂直的判定定理,则AB1⊥平面C1DF.
【解答】
解:作DE⊥AB1交AB1于E,延长DE交BB1于F,
连接C1F,则AB1⊥平面C1DF,点F即为所求.
若AB1⊥平面C1DF,则AB1⊥DF,
故F在边界BB1上时,C1F的长取到最大值,
此时因为AB1⊥DF,
故∠FDB1+∠AB1A1=∠B1AA1+∠AB1A1=90°,
故∠FDB1=∠B1AA1,
故tan∠FDB1=tan∠B1AA1,即FB1DB1=A1B1AA1,
故FB1=A1B1?DB1AA1=22+22×22+2224=1
故选A.
5.【答案】A
【解析】
【分析】本题考查空间中的距离.因为A,B两点在α同侧,根据中点坐标公式求解.
【解答】如图,设AB的中点为M,分别过A,M,B向α作垂线,垂足分别为A1,M1,B1,则由线面垂直的性质定理可知AA1?//?MM1?//?BB1.结合题意知,四边形AA1B1B为直角梯形,AA1=3,BB1=5,MM1为其中位线,∴MM1=4.故选A.
6.【答案】A
【解析】
【分析】
本题考查空间直线和直线垂直的判定,考查线面垂直的判定与性质,属于中档题,A条件加入,可判断出AC与EF垂直,这样EF和平面ABDC内两条相交线垂直,得到EF与平面ABDC垂直的结论,从而证出结论,条件BC只能得到ABDC为矩形,得不到所要结论,条件D而举反例说明错误.
【解答】
解:AB⊥α,CD⊥α,则AB和CD平行,AB和CD确定平面为平面ABDC,
增加条件A,由AB⊥α,CD⊥α,EF?α,得AB⊥EF,
AC⊥β,EF在平面β内,故 AC⊥EF,则EF与平面ABDC内两条相交直线AC,AB都垂直,
由线面垂直的判这定定理,EF⊥平面ABDC,BD在平面ABDC内,?
所以BD⊥EF,A正确;
增加条件B,C只能得到ABDC为矩形的结论,BD和EF同在平面α内,
BD和EF平行,相交或重合的可能性都有,也包括垂直,
BD⊥EF不一定成立,故 B,C错误;
不妨设ABCD是一个矩形,且BD和EF平行,此时AC和BD平行,
AC与EF与平行,AC与两平面α,β成等角,但BD⊥EF不成立,故D错误,
故选A.
7.【答案】ABC
【解析】
【分析】
本题考查面面平行的判定与性质,线面垂直的判定,涉及正方体的结构特征,属基础题.
根据AB=AA1=AD,可以得到A到△A1BD各顶点的距离相等,可得A正确;利用面面平行的判定定理平面CB1D1//平面A1BD,于是得到AH⊥平面CB1D1,判定B;连接AC1,利用线面垂直的判定定理可得AC1⊥平面A1BD,从而判定C;利用异面直线所成角的定义可得直线AH和BB1所成角为∠A1AC1,判定不是45°,从而判定D.
【解答】
解:∵△A1BD为等边三角形,∴其四心合一,
又∵AB=AA1=AD,
∴A到△A1BD各顶点的距离相等,∴A正确.
∵CD1//BA1,CB1//DA1,CD1∩CB1=C,BA1∩DA1=A1,
CD1、CB1?平面CB1D1,BA1、DA1?平面A1BD,
∴平面CB1D1//平面A1BD,
∴AH⊥平面CB1D1,∴B正确.
连接AC1,则AC1⊥BD,AC1⊥BA1,又BD∩BA1=B,
BD、BA1?平面A1BD,
∴AC1⊥平面A1BD,∴A,H,C1三点共线,
∴C正确.
∵直线AH和BB1所成角为∠A1AC1,而AA1≠A1C1,∴∠A1AC1≠45°,故D错误,
故选ABC.
8.【答案】ABD
【解析】
【分析】
本题考查线面垂直的判定与性质,属于基础题.
根据线面垂直的判定与性质逐项判断,即可得到答案.
【解答】
解:由PA⊥平面ABC,BC?平面ABC,
得PA⊥BC,所以A正确;
又BC⊥AC,PA∩AC=A,PA,AC?平面PAC,
∴BC⊥平面PAC,
又PC?平面PAC,
∴BC⊥PC,所以B,D均正确.
若AC⊥PB,又因为BC⊥AC,PB∩BC=B,PB,BC?平面PBC,
所以AC⊥平面PBC,
又PC?平面PBC,
则AC⊥PC,
又PA⊥平面ABC,AC?平面ABC,则PA⊥AC,产生矛盾,故C不正确.
故选ABD.
9.【答案】B
【解析】
【分析】
本题考查线线、线面、面面的位置关系及线面平行、线面垂直的判定定理.
连接AC、BD相交于点O,连接EM,EN,SO.(1)先证明AC⊥平面SBD,再利用三角形的中位线可得EM//BD,MN//SD,于是平面EMN//平面SBD,进而得到AC⊥平面EMN,AC⊥EP;(2)当点P与点M不重合时,由异面直线的定义可知:EP与BD是异面直线,因此不可能EP//BD;(3)由(1)可知:平面EMN//平面SBD,可得EP//平面SBD;(4)由(1)同理可得:EM⊥平面SAC,可用反证法证明:当P与M不重合时,EP与平面SAC不垂直.
【解答】
解:如图所示,连接AC、BD相交于点O,连接EM,EN,SO.
(1)由正四棱锥S?ABCD,可得SO⊥底面ABCD,AC⊥BD,
又AC?底面ABCD,
∴SO⊥AC.
∵SO∩BD=O,SO、BD?平面SBD,
∴AC⊥平面SBD,
∵E,M,N分别是BC,CD,SC的中点,
∴EM//BD,MN//SD,
∵MN,EM?平面SBD,SD,BD?平面SBD,
∴EM//平面SBD,MN//平面SBD,
而EM∩MN=M,EM、MN?平面EMN,
∴平面EMN//平面SBD,∴AC⊥平面EMN,
又EP?平面EMN,
∴AC⊥EP.故正确.
(2)当点P与点M重合时,有EP//BD;
当点P与点M不重合时,由异面直线的定义可知:EP与BD是异面直线,不可能EP//BD,
因此EP//BD不恒成立;
(3)由(1)可知:平面EMN//平面SBD,又EP?平面EMN,∴EP//平面SBD,因此正确.
(4)由(1)可得:SO⊥底面ABCD,又BD?底面ABCD,∴SO⊥BD.
又AC⊥BD,AC∩SO=O,SO、AC?平面SAC,
∴BD⊥平面SAC,又EM//BD,∴EM⊥平面SAC,
当点P与点M重合时,满足EP⊥面SAC;
当点P与点M不重合时,
若EP⊥平面SAC,则EP//EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.
因此EP⊥面SAC不恒成立.
综上可知:只有(1)(3)正确.即四个结论中恒成立的个数是2.
故选:B.
10.【答案】D
【解析】
【分析】
本题考查空间两平面平行的判定,属于基础题.
根据两平面平行的判定定理和推论,可得结论.
【解答】
解:两条平行直线分别在两个平面内,这两个平面有可能相交,排除A;
一个平面的两条直线都平行于另一个平面,这两个平面有可能相交,排除B;
两个平面都垂直于同一个平面,这两个平面有可能相交,排除C;
垂直于同一条直线的两个平面平行,D正确。
故选D
11.【答案】D
【解析】
【分析】
本题考查空间距离有计算,涉及线面垂直的性质的应用,属于基础题.
由已知两根旗杆所在的直线平行,由已知构造直角三角形求解即可.
【解答】
解:设AB,CD分别为两根旗杆所在的线段,
如图,由线面垂直的性质定理可知AB?//?CD,作AE⊥CD于E,则DE=b?c,
故AD=a2+(b?c)2.
故选D.
12.【答案】1
【解析】
【分析】
本题主要考查了线面垂直的判定,注意空间思维能力的培养.
证明BC'⊥平面AC'D,结合EF⊥平面AC'D,由线面垂直的性质得到EF?//?BC',即可求得λ的值.
【解答】
解:∵点C'在平面ABD上的射影O在AB上,∴C'O⊥平面ABD.
∵DA?平面ABD,∴C'O⊥DA.又∵AD⊥AB,AB∩C'O=O,
∴DA⊥平面ABC'.
又BC'?平面ABC',∴DA⊥BC'.
又∵BC'⊥C'D,DA∩C'D=D,∴BC'⊥平面AC'D.
又∵EF⊥平面AC'D,∴EF?//?BC'.∵DC'=2DE,即E为C'D的中点,∴F为BD的中点,
∴BF=FD,即λ=1.
13.【答案】532
【解析】解:如图所示,
三棱锥P?ABC中,PA⊥平面ABC,
∴PA⊥AB,PA⊥AC,PA⊥BC;
又AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥PC;
∴三棱锥P?ABC的各个面都是直角三角形;
又BC=PA=3,AC=1,
∴三棱锥P?ABC的侧面积为
S侧面积=S△PAB+S△PAC+S△PBC
=12×3×(3)2+12+12×3×1+12×3×(3)2+12
=532.
故答案为:532.
根据题意画出图形,证明三棱锥P?ABC的各个面都是直角三角形,再求三棱锥的侧面面积.
本题考查了三棱锥的结构特征与空间中的垂直关系应用问题,是基础题.
14.【答案】6
【解析】
【分析】
本题考查的是直线与平面垂直关系的应用,解题的关键是熟练掌握直线与平面垂直的性质;经审题,根据直线和平面垂直的性质定理知AF//DE,结合已知条件可判断出四边形AFED的形状;四边形AFED为平行四边形,根据平行四边形的性质即可得到本题答案.
【解答】
解:∵AF⊥平面ABCD,DE⊥平面ABCD,∴AF//DE,又∵AF=DE,∴四边形AFED是平行四边形,
∴EF=AD=6,
故答案为6.
15.【答案】?①?②?③
【解析】
【分析】
本题考查线面垂直的性质定理、面面平行的性质定理、平行公理以及空间两条直线的位置关系,属于基础题.
对于?①,利用线面垂直的性质即可判断为正确;
对于?②,利用面面平行的性质即可判断为正确;
对于?③,应用平行公理即可判断为正确;
对于?④,a,b可能平行、异面和垂直三种情况,?④错误.
【解答】
解:对于?①,利用线面垂直的性质可知?①正确;对于?②,由于a,b共面,利用面面平行的性质即可判断a//b,故?②正确;对于?③,应用平行公理可知?③正确;对于?④,当a和b在正方体的两个平行面内,且与正方体的同一条棱垂直时,a,b可能平行、异面和垂直三种情况,故?④错误.
故答案为:?①?②?③
16.【答案】1
【解析】
【分析】
本题考查平面到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
根据正方体的结构特征可知AB⊥平面BB1C1C,且AB⊥平面AA1D1D,即可得知棱AB的长即为所求.
【解答】
解:因为正方体的对面互相平行,
AB⊥平面BB1C1C,且AB⊥平面AA1D1D,
所以棱AB的长即为平面BB1C1C与平面AA1D1D的距离,且距离为1.
故答案为:1.
17.【答案】323π
【解析】
【分析】
本题考查球内接多面体,考查球的体积,考查学生的计算能力,比较基础.
由题意把A、B、C、D扩展为三棱柱如图,求出上下底面中心连线的中点与A的距离为球的半径,然后求出球的体积.
【解答】
解:由题意画出几何体的图形如图,
把A、B、C、D扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
AD=2AB=6,OE=3,△ABC是正三角形,
所以AE=23AB2?(12AB)2=3.
R=AO=32+3=23,可得球的体积为4πR33=323π.
故答案为:323π.
18.【答案】解:(1)由题意可得BC//B1C1,
∴∠A1CB(或其补角)即为异面直线B1C1与A1C所成的角,
由题意可知BB1⊥平面ABC,BC?平面ABC,
∴BB1⊥BC,
又AB⊥BC,AB∩BB1=B,AB?平面ABB1A1,BB1?平面ABB1A1,
∴BC⊥平面ABB1A1,
∵A1B?平面ABB1A1,∴BC⊥A1B,
∴△A1BC为直角三角形,
∴tan∠A1CB=A1BBC=AB2+BB12BC=5,
∴异面直线B1C1与A1C所成的角的正切值为5;
(2)∵BC//B1C1,BC?平面A1BC,B1C1?平面A1BC,
∴B1C1//平面A1BC,
∴直线B1C1上任意一点到平面A1BC的距离均为直线B1C1到平面A1BC的距离,
不妨取B1,且设B1到平面A1BC的距离为h,
由等体积法可得VB1?A1BC=VC?A1BB1,即13S△A1BC×?=13S△ABB1×BC,
代入数据可得13×12×1×5×?=13×12×2×1×1,解得?=255,
∴直线B1C1到平面A1BC的距离为255.
【解析】本题考查异面直线所成的角,涉及直线到平面的距离,等体积是解决问题的关键,属中档题.
(1)由题意可得∠A1CB(或其补角)即为异面直线B1C1与A1C所成的角,解三角形可得;
(2)可证B1C1//平面A1BC,则B1到平面A1BC的距离h即为所求,由等体积法可得VB1?A1BC=VC?A1BB1,代入数据计算可得.
19.【答案】解:(1)∵AD?//?BC,AD?平面PBC,BC?平面PBC,
∴AD?//平面PBC,
∴AD到平面PBC的距离等于点A到平面PBC的距离,
过点A作AH⊥PB,交PB于H,如图所示,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵BC⊥AB,PA∩AB=A,PA,AB?平面PAB,
∴BC⊥平面PAB,?
又AH?平面PAB,
∴BC⊥AH,?
又AH⊥PB,PB∩BC=B,PB,BC?平面PBC,
∴AH⊥平面PBC,
∴AH的长即为点A到平面PBC的距离,也即直线AD到平面PBC的距离,
在等腰直角三角形PAB中,易得AH=22a,
所以直线AD到平面PBC的距离为22a.
(2)过点A作AE⊥PC,交PC于E,则AE的长即为点A到PC的距离.连接AC,
在Rt△PAC中,PA=a,AC=2a,PC=3a,
∵AE·PC=PA·AC,
∴AE=PA?ACPC=63a,即点A到直线PC的距离为63a.
(3)假设在线段AD上存在一点F,使点A到平面PCF的距离为63a,
过点C作CM⊥AD,交AD于M,
在Rt△CMD中,CM=a,cos∠MDC=255,可得CD=5a,DM=2a,
所以AD=3a.? 由(2)知AE=63a,
若存在满足题意的F,则只需AE⊥平面PCF,
由条件可知,只需AC⊥CF,
设DF=x,则AF=3a?x,?
在△CDF中,由余弦定理可得CF2=x2+5a2?4ax,
若AC⊥CF,则在Rt△ACF中,AF2=CF2+AC2,?
即(3a?x)2=2a2+x2+5a2?4ax,解得x=a,?
即在AD上存在一点F,当AF=2a时,AC⊥CF,
又PA⊥CF,PA∩AC=A,
∴CF⊥平面PAC,
∴CF⊥AE,又AE⊥PC,PC∩CF=C,
∴AE⊥平面PCF,即点A到平面PCF的距离为AE=63a.
【解析】本题主要考查空间距离,属于中档题.
(1)由线面垂直的判断得AH⊥平面PBC,在三角形中求AH,得答案;
(2)过点A作AE⊥PC,交PC于E,则AE的长即为点A到PC的距离.在Rt△PAC中,由AE·PC=PA·AC,求解AE得答案;
(3)假设在线段AD上存在一点F,使点A到平面PCF的距离为63a,过点C作CM⊥AD,交AD于M,若存在满足题意的F,则只需AE⊥平面PCF,由线面垂直得点A到平面PCF的距离.
20.【答案】证明:(1)由题设知AB=BC=1,AC=2,
∴AB2+BC2=AC2,∴AB⊥BC,
∵PA⊥平面ABC,∴PA⊥BC,PA⊥AB,
∵PA∩AB=A,∴BC⊥平面PAB.
解:(2)点D为PC的中点,且PD=32,使得AC⊥BD.
理由如下:
在平面ABC内,过点B作BE⊥AC,垂足为E,
在平面PAC内,过点E作DE//PA,交PC于点D,连结BD,
由PA⊥平面ABC,知PA⊥AC,∴DE⊥AC,
∴AC⊥平面DBE,
∵BD?平面DBE,∴AC⊥BD,
在△ABC中,AB=BC=1,点E为AC的中点,则点D为PC的中点,
在Rt△APC中,AP=1,AC=2,∴PC=3,
∴PD=32.
【解析】(1)推导出AB⊥BC,PA⊥BC,PA⊥AB,由此能证明BC⊥平面PAB.
(2)过点B作BE⊥AC,垂足为E,过点E作DE//PA,交PC于点D,连结BD,推导出PA⊥AC,DE⊥AC,从而AC⊥平面DBE,进而AC⊥BD,由此能求出点D为PC的中点,且PD=32,使得AC⊥BD.
本题考查线面垂直的证明,考查满足线线垂直的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
