6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案)
文档属性
| 名称 | 6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 238.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 15:11:53 | ||
图片预览


文档简介
6.1平面向量的概念同步练习
选择题
1.下列说法中正确的个数是( )
①身高是一个向量;
②∠AOB的两条边都是向量;
③温度含零上温度和零下温度,所以温度是向量;
④物理学中的加速度是向量.
A.0 B.1 C.2 D.3
2.下列说法正确的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
3.已知点O固定,且,则点A的轨迹是( )
A.一个点 B.一条直线 C.一个圆 D.不能确定
4.如图,在⊙O中,向量,,是( )
A.有相同起点的向量 B.共线向量
C.模相等的向量 D.相等的向量
5.如图,四边形ABCD中,=,则相等的向量是( )
A.与 B.与 C.与 D.与
6.下列说法正确的是( )
A.两个有共同起点而且相等的向量,其终点必相同
B.长度相等的向量叫作相等向量
C.共线向量是在一条直线上的向量
D.向量与向量平行,则与的方向相同或相反
7.下列说法正确的是( )
A.长度相等的向量叫相等向量
B.零向量的长度为零
C.共线向量是在一条直线上的向量
D.平行向量就是向量所在的直线平行的向量
8.设是两个单位向量,则下列结论中正确的是( )
A. B. C. D.
9.下列结论中,不正确的是( )
A.向量,共线与向量∥意义是相同的
B.若向量=,则∥
C.若向量,满足||=||,就有=
D.若向量=,则向量=
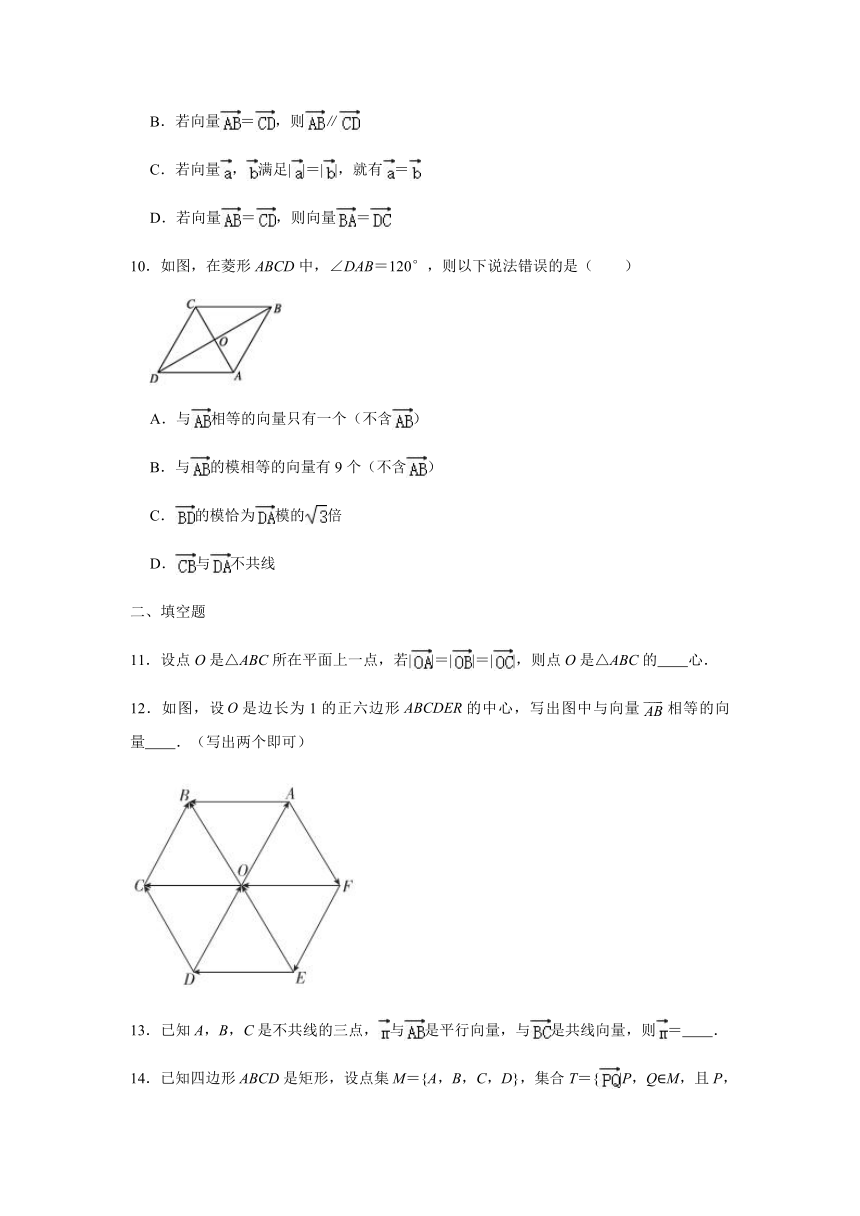
10.如图,在菱形ABCD中,∠DAB=120°,则以下说法错误的是( )
A.与相等的向量只有一个(不含)
B.与的模相等的向量有9个(不含)
C.的模恰为模的倍
D.与不共线
填空题
11.设点O是△ABC所在平面上一点,若||=||=||,则点O是△ABC的 心.
12.如图,设是边长为1的正六边形的中心,写出图中与向量相等的向量 .(写出两个即可)
13.已知A,B,C是不共线的三点,与是平行向量,与是共线向量,则= .
14.已知四边形ABCD是矩形,设点集M={A,B,C,D},集合T={|P,Q∈M,且P,Q不重合},用列举法表示集合T= .
解答题
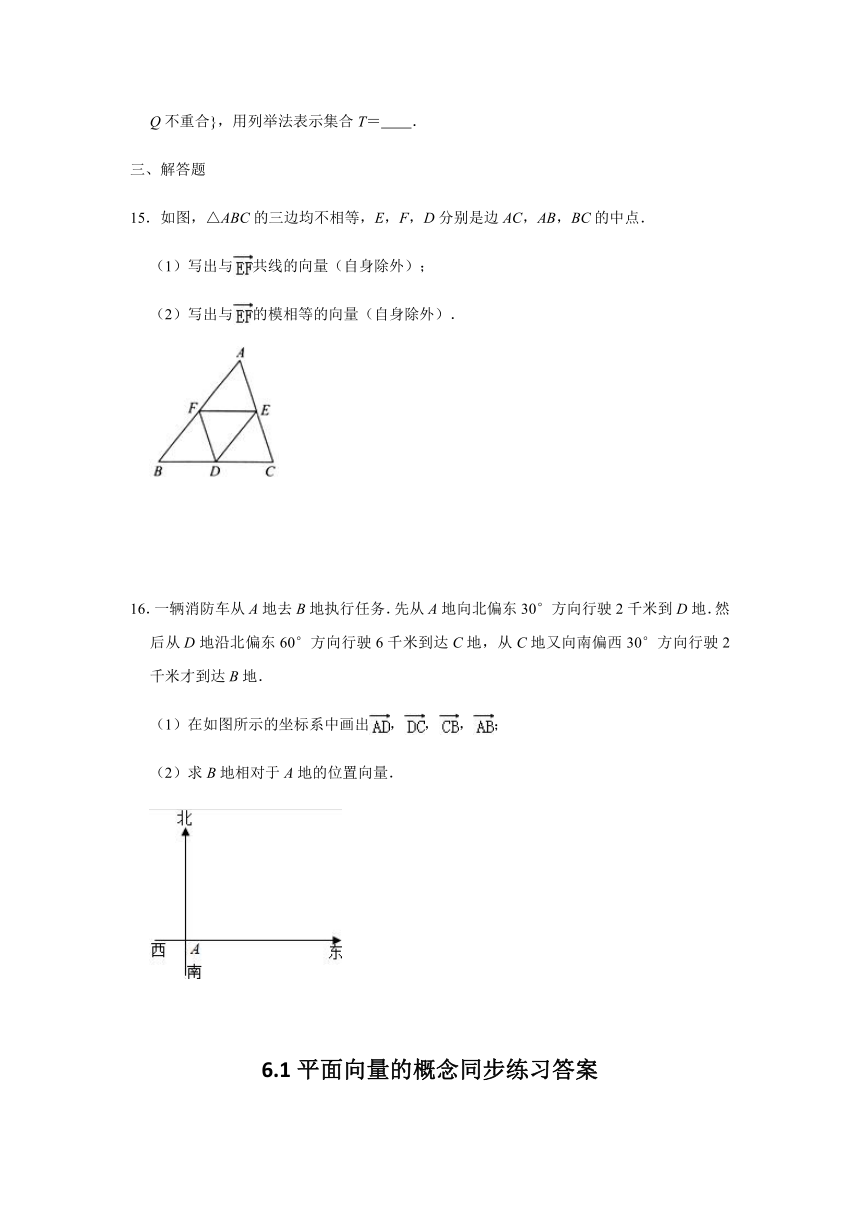
15.如图,△ABC的三边均不相等,E,F,D分别是边AC,AB,BC的中点.
(1)写出与共线的向量(自身除外);
(2)写出与的模相等的向量(自身除外).
16.一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
(1)在如图所示的坐标系中画出,,,;
(2)求B地相对于A地的位置向量.
6.1平面向量的概念同步练习答案
1.解:对于①身高只有大小,没有方向,所以不是向量;
②温度的零上和零下表示温度的大小,温度没有方向,所以温度不是向量;
③角的边是没有大小和方向的,角是计算角度的,所以∠AOB的两条边都不是向量;
④物理学中的加速度既有大小又有方向是向量.
综上可得④正确,
故选:B.
2.解:对于A,数量可以比较大小,向量是矢量,不能比较大小,A错误;
对于B,向量是矢量,不能比较大小,∴B错误;
对于C,向量的大小与方向无关,∴C错误;
对于D,向量的模长是数量,可以比较大小,∴D正确.
故选:D.
3.解:∵,∴|OA|=2,
∴点A的轨迹是以O为圆心,以2为半径的圆,
故选:C.
4.解:对于A:根据图形,可得向量,,不是相同起点的向量;∴A不对;
对于B:共线向量知识点方向相同或者相反的向量,∴B不对;
对于C:因为O是圆心,那么向量,,的模长的一样的,∴C对;
对于D:相等的向量指的是大小相等,方向相同的向量,∴D不对;
故选:C.
5.解:∵四边形ABCD中,=,∴四边形ABCD是平行四边形,
∴.
故选:D.
6.解:对于A:两个有共同起点而且相等的向量,其终点必相同,A正确;
对于B:长度相等,方向相同的向量叫作相等向量,B错误;
对于C:共线向量是方向相同或方向相反的向量,C错误;
对于D:向量与向量平行,则与的方向相同或相反,也可能是0向量,错误;
故选:A.
7.解:大小相等、方向相同的向量叫相等向量,∴A错误;
零向量的长度为0,∴B正确;
方向相同或相反的向量叫共线向量,它们不一定在同一条直线上,∴C错误;
平行向量就是向量所在的直线平行的向量,也可以共线,∴D错误;
故选:B.
8.解:∵是两个单位向量,∴,
故选:D.
9.解:选项A,由向量共线的定义可得向量,共线与向量∥意义是相同的,故正确;
选项B,当向量=,则一定有∥,故正确;
选项C,向量,满足||=||,但方向不定,故不一定有=,故错误;
选项D,由向量=和相反向量可得向量=,故正确.
故选:C.
10.解:A.与相等的向量只有一个(不含)是,正确;
B.在菱形ABCD中,∠DAB=120°,∴∠ADC=60°,因此△ADC和△ABC都是等边三角形.
∴与的模相等的向量有9个(不含):,,,,,,,,.因此正确.
C.由等边三角形的性质可得:,∴.
因此的模恰为模的倍,故正确.
D.∵,∴与共线,故D不正确.
综上可知:只有D不正确.
故选:D.
11.解:∵点O是△ABC所在平面上一点,
||=||=||,
∴点O在△ABC所在平面内,且点O到△ABC的三个顶点的距离相等,
∴点O是△ABC的外心.
故答案为:外.
12.解:由题可得:与相等的向量是:,,;
故答案为:,,.
13.解:A,B,C是不共线的三点,
则与不共线,
与是平行向量,与是共线向量,则=.
故答案为:.
14.解:∵点集M={A,B,C,D},集合T={|P,Q∈M,且P,Q不重合},
∴T={,,,,,,,},
故答案为:{,,,,,,,}.
15.解:(1)与共线的向量有:,,,,,,;
(2)与的模相等的向量有:,,,,.
16.解:(1)作出向量如图所示:
(2)∵D在A北偏东30°方向上,B在C南偏西30方向上,∴AD∥BC,
∵AD=BC=2,∴四边形ABCD是平行四边形,∴AB=DC=6,
∵C在D北偏东60°方向上,∴B在A北偏东60°方向6千米处.
∴的方向为北偏东60°,||=6.
选择题
1.下列说法中正确的个数是( )
①身高是一个向量;
②∠AOB的两条边都是向量;
③温度含零上温度和零下温度,所以温度是向量;
④物理学中的加速度是向量.
A.0 B.1 C.2 D.3
2.下列说法正确的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
3.已知点O固定,且,则点A的轨迹是( )
A.一个点 B.一条直线 C.一个圆 D.不能确定
4.如图,在⊙O中,向量,,是( )
A.有相同起点的向量 B.共线向量
C.模相等的向量 D.相等的向量
5.如图,四边形ABCD中,=,则相等的向量是( )
A.与 B.与 C.与 D.与
6.下列说法正确的是( )
A.两个有共同起点而且相等的向量,其终点必相同
B.长度相等的向量叫作相等向量
C.共线向量是在一条直线上的向量
D.向量与向量平行,则与的方向相同或相反
7.下列说法正确的是( )
A.长度相等的向量叫相等向量
B.零向量的长度为零
C.共线向量是在一条直线上的向量
D.平行向量就是向量所在的直线平行的向量
8.设是两个单位向量,则下列结论中正确的是( )
A. B. C. D.
9.下列结论中,不正确的是( )
A.向量,共线与向量∥意义是相同的
B.若向量=,则∥
C.若向量,满足||=||,就有=
D.若向量=,则向量=
10.如图,在菱形ABCD中,∠DAB=120°,则以下说法错误的是( )
A.与相等的向量只有一个(不含)
B.与的模相等的向量有9个(不含)
C.的模恰为模的倍
D.与不共线
填空题
11.设点O是△ABC所在平面上一点,若||=||=||,则点O是△ABC的 心.
12.如图,设是边长为1的正六边形的中心,写出图中与向量相等的向量 .(写出两个即可)
13.已知A,B,C是不共线的三点,与是平行向量,与是共线向量,则= .
14.已知四边形ABCD是矩形,设点集M={A,B,C,D},集合T={|P,Q∈M,且P,Q不重合},用列举法表示集合T= .
解答题
15.如图,△ABC的三边均不相等,E,F,D分别是边AC,AB,BC的中点.
(1)写出与共线的向量(自身除外);
(2)写出与的模相等的向量(自身除外).
16.一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
(1)在如图所示的坐标系中画出,,,;
(2)求B地相对于A地的位置向量.
6.1平面向量的概念同步练习答案
1.解:对于①身高只有大小,没有方向,所以不是向量;
②温度的零上和零下表示温度的大小,温度没有方向,所以温度不是向量;
③角的边是没有大小和方向的,角是计算角度的,所以∠AOB的两条边都不是向量;
④物理学中的加速度既有大小又有方向是向量.
综上可得④正确,
故选:B.
2.解:对于A,数量可以比较大小,向量是矢量,不能比较大小,A错误;
对于B,向量是矢量,不能比较大小,∴B错误;
对于C,向量的大小与方向无关,∴C错误;
对于D,向量的模长是数量,可以比较大小,∴D正确.
故选:D.
3.解:∵,∴|OA|=2,
∴点A的轨迹是以O为圆心,以2为半径的圆,
故选:C.
4.解:对于A:根据图形,可得向量,,不是相同起点的向量;∴A不对;
对于B:共线向量知识点方向相同或者相反的向量,∴B不对;
对于C:因为O是圆心,那么向量,,的模长的一样的,∴C对;
对于D:相等的向量指的是大小相等,方向相同的向量,∴D不对;
故选:C.
5.解:∵四边形ABCD中,=,∴四边形ABCD是平行四边形,
∴.
故选:D.
6.解:对于A:两个有共同起点而且相等的向量,其终点必相同,A正确;
对于B:长度相等,方向相同的向量叫作相等向量,B错误;
对于C:共线向量是方向相同或方向相反的向量,C错误;
对于D:向量与向量平行,则与的方向相同或相反,也可能是0向量,错误;
故选:A.
7.解:大小相等、方向相同的向量叫相等向量,∴A错误;
零向量的长度为0,∴B正确;
方向相同或相反的向量叫共线向量,它们不一定在同一条直线上,∴C错误;
平行向量就是向量所在的直线平行的向量,也可以共线,∴D错误;
故选:B.
8.解:∵是两个单位向量,∴,
故选:D.
9.解:选项A,由向量共线的定义可得向量,共线与向量∥意义是相同的,故正确;
选项B,当向量=,则一定有∥,故正确;
选项C,向量,满足||=||,但方向不定,故不一定有=,故错误;
选项D,由向量=和相反向量可得向量=,故正确.
故选:C.
10.解:A.与相等的向量只有一个(不含)是,正确;
B.在菱形ABCD中,∠DAB=120°,∴∠ADC=60°,因此△ADC和△ABC都是等边三角形.
∴与的模相等的向量有9个(不含):,,,,,,,,.因此正确.
C.由等边三角形的性质可得:,∴.
因此的模恰为模的倍,故正确.
D.∵,∴与共线,故D不正确.
综上可知:只有D不正确.
故选:D.
11.解:∵点O是△ABC所在平面上一点,
||=||=||,
∴点O在△ABC所在平面内,且点O到△ABC的三个顶点的距离相等,
∴点O是△ABC的外心.
故答案为:外.
12.解:由题可得:与相等的向量是:,,;
故答案为:,,.
13.解:A,B,C是不共线的三点,
则与不共线,
与是平行向量,与是共线向量,则=.
故答案为:.
14.解:∵点集M={A,B,C,D},集合T={|P,Q∈M,且P,Q不重合},
∴T={,,,,,,,},
故答案为:{,,,,,,,}.
15.解:(1)与共线的向量有:,,,,,,;
(2)与的模相等的向量有:,,,,.
16.解:(1)作出向量如图所示:
(2)∵D在A北偏东30°方向上,B在C南偏西30方向上,∴AD∥BC,
∵AD=BC=2,∴四边形ABCD是平行四边形,∴AB=DC=6,
∵C在D北偏东60°方向上,∴B在A北偏东60°方向6千米处.
∴的方向为北偏东60°,||=6.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
