2020-2021学年河北省邢台市临西县七年级(下)期末数学试卷 (word版含解析)
文档属性
| 名称 | 2020-2021学年河北省邢台市临西县七年级(下)期末数学试卷 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 08:19:03 | ||
图片预览




文档简介
2020-2021学年河北省邢台市临西县七年级(下)期末数学试卷
一、选择题(共14个小题,每小题3分,共42分.)
1.实数是( )
A.分数 B.无理数 C.有理数 D.整数
2.如图,在一张透明的纸上画一条直线l,在l外任取一点Q并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
3.在平面直角坐标系中,点A(0,﹣2)在( )
A.x轴的负半轴上 B.y轴的负半轴上
C.x轴的正半轴上 D.y轴的正半轴上
4.用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
5.为了了解邢台市老年人的健康状况,在以下的抽样调查中,你认为样本选择较合适的是( )
A.在达活泉晨练的100位老人
B.到邢台人民医院随机抽查的100位住院老人
C.到某养老院随机抽查的100位老人
D.从全市户籍管理系统任意抽取100位老人
6.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
7.将一块体积为64cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )
A.2cm B.3cm C.4cm D.5cm
8.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
9.如图,表示实数(1﹣)的点落在( )
A.段① B.段② C.段③ D.段④
10.下列调查:①了解夏季冷饮市场上冰淇淋的质量;②了解李红同学60道英语选择题的通过率;③了解一批导弹的杀伤范围;④了解全世界网迷少年的性格情况.不适合普查而适合做抽样调查的是( )
A.①②④ B.①③④ C.②③④ D.①②③
11.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(大于等于60)的有12人
12.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将(1)×2+(2)×3
B.要消去x,可以将(1)×3+(2)×(﹣5)
C.要消去y,可以将(1)×5+(2)×3
D.要消去x,可以将(1)×(﹣5)+(2)×3
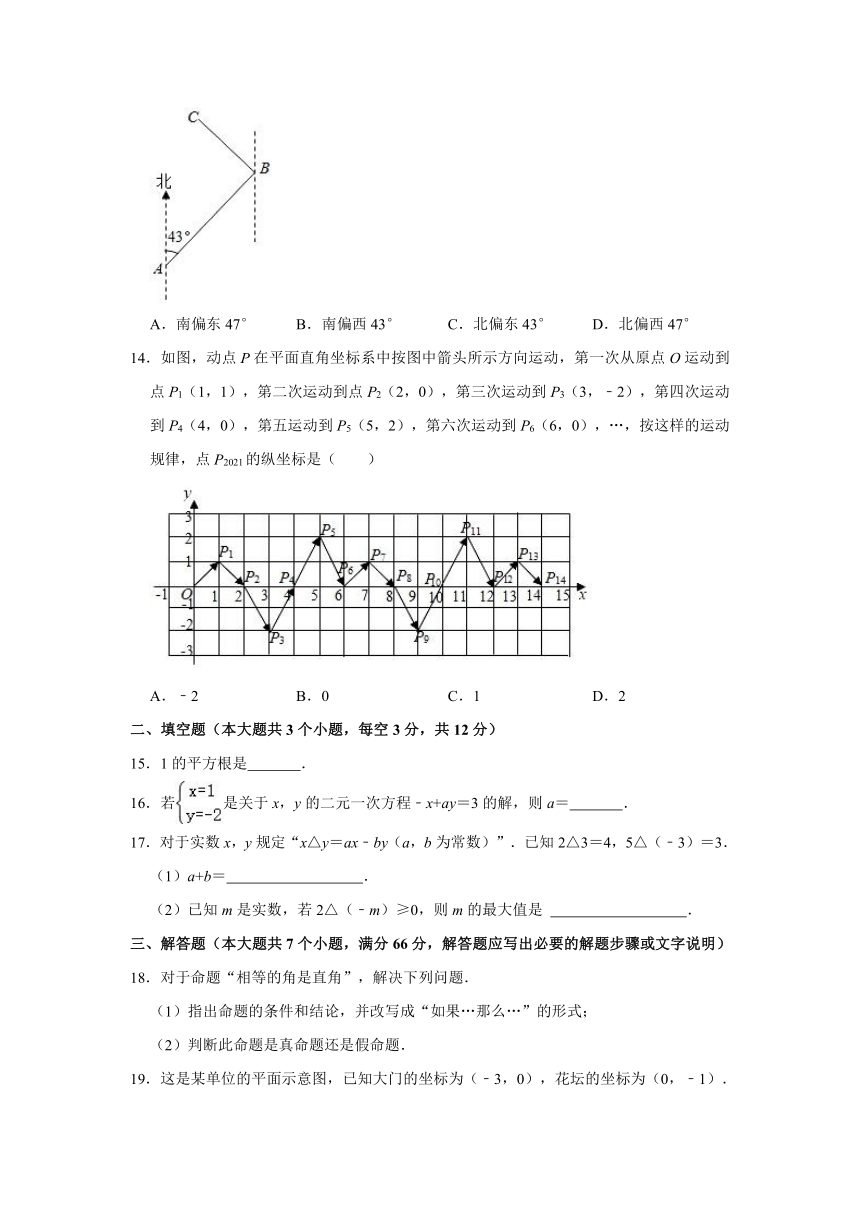
13.如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地的方位角是北偏东43°,那么从C地测B地的方位角是( )
A.南偏东47° B.南偏西43° C.北偏东43° D.北偏西47°
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
二、填空题(本大题共3个小题,每空3分,共12分)
15.1的平方根是 .
16.若是关于x,y的二元一次方程﹣x+ay=3的解,则a= .
17.对于实数x,y规定“x△y=ax﹣by(a,b为常数)”.已知2△3=4,5△(﹣3)=3.
(1)a+b= .
(2)已知m是实数,若2△(﹣m)≥0,则m的最大值是 .
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的解题步骤或文字说明)
18.对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果…那么…”的形式;
(2)判断此命题是真命题还是假命题.
19.这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系.
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
20.新冠肺炎疫情爆发以来,党中央高度重视,带领全国人民众志成城,严防严控,以惊人的速度取得了阶段性胜利.某市教育主管部门响应上级号召,在初中生中开展了“新冠病毒预防知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(均为整数,总分100分),绘制了如图尚不完的统计图表.
调查结果统计表:
组别 成绩分组(单位:分) 频数
A 80≤x<85 50
B 85≤x<90 75
C 90≤x<95 150
D 95≤x≤100 a
合计
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量是 .
(2)统计表中,a= .
(3)扇形统计图中,m的值为 ,“C”所对应的圆心角的度数为 ;
(4)若参加本次知识竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
21.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m2的正方形场地改建成300m2的长方形场地,且其长、宽的比为5:3.
(1)求原来正方形场地的周长.
(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.
22.在平面直角坐标系中,点P的坐标为(a﹣7,3﹣2a),将点P向上平移4个单位,再向右平移5个单位后得到点Q.
(1)若点Q位于第一象限,求a的取值范围.
(2)若a为整数,求出P、Q两点坐标.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.
(1)求毛笔和宣纸的单价;
(2)某超市给出以下两种优惠方案:
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折.
学校准备购买毛笔50支,宣纸若干张(超过200张).选择哪种方案更划算?请说明理由.
参考答案
一、选择题(本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.实数是( )
A.分数 B.无理数 C.有理数 D.整数
【分析】根据无理数的定义即可判断.
解:∵是无限不循环小数,
∴是无理数,
∴是无理数,
故选:B.
2.如图,在一张透明的纸上画一条直线l,在l外任取一点Q并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
【分析】根据垂线的基本性质:过直线上或直线外的一点,有且只有一条直线和已知直线垂直,容易判断.
解:根据垂线的性质,这样的直线只能作一条,
故选:B.
3.在平面直角坐标系中,点A(0,﹣2)在( )
A.x轴的负半轴上 B.y轴的负半轴上
C.x轴的正半轴上 D.y轴的正半轴上
【分析】根据y轴上的横坐标等于零,y轴上纵坐标小于零的点在y轴的负半轴上,可得答案.
解:在平面直角坐标系中,点A(0,﹣2)在y轴的负半轴上,
故选:B.
4.用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
【分析】不等式的解集在数轴上表示出来的方法:“>”空心圆点向右画折线,“≥”实心圆点向右画折线,“<”空心圆点向左画折线,“≤”实心圆点向左画折线.
解:本题可观察数轴向右画又是实心圆,因此是x≥﹣2.
故选:C.
5.为了了解邢台市老年人的健康状况,在以下的抽样调查中,你认为样本选择较合适的是( )
A.在达活泉晨练的100位老人
B.到邢台人民医院随机抽查的100位住院老人
C.到某养老院随机抽查的100位老人
D.从全市户籍管理系统任意抽取100位老人
【分析】根据抽取样本的代表性、可靠性,结合具体的情景进行判断即可.
解:A.在达活泉晨练的100位老人,不具有代表性,所得结果的可靠性不高,因此选项A不符合题意;
B.到邢台人民医院随机抽查的100位住院老人,这样所得的结果具有片面性,可靠性不高,因此选项B不符合题意;
C.到某养老院随机抽查的100位老人,不具有代表性,所得结果的可靠性不高,因此选项C不符合题意;
D.从全市户籍管理系统任意抽取100位老人,这样取样具有代表性,广泛性,可靠性较强,因此选项D符合题意;
故选:D.
6.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是C.
解:观察图形可知图案C通过平移后可以得到.
故选:C.
7.将一块体积为64cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )
A.2cm B.3cm C.4cm D.5cm
【分析】利用立方根定义求出棱长即可.
解:根据题意知,每个小正方体木块的棱长为==2(cm),
故选:A.
8.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
【分析】根据各选项的表述列出个不等式,与选项中所表示的比对即可得出答案.
【解答】A、a不是负数,可表示成a≥0,故本选项错误;
B、x不大于3,可表示成x≤3,故本选项错误;
C、m与4的差是负数,可表示成m﹣4<0,故本选项正确;
D、x与2的和是非负数,可表示成x+2≥0,故本选项错误.
故选:C.
9.如图,表示实数(1﹣)的点落在( )
A.段① B.段② C.段③ D.段④
【分析】先确定的近似值,然后求出1﹣的值,再对应数轴上的每一段范围即可确定答案.
解:∵≈1.732…,
∴1﹣≈﹣0.732…,
∵段③的范围是﹣1~0,
∴表示(1﹣)的点落在段③.
故选:C.
10.下列调查:①了解夏季冷饮市场上冰淇淋的质量;②了解李红同学60道英语选择题的通过率;③了解一批导弹的杀伤范围;④了解全世界网迷少年的性格情况.不适合普查而适合做抽样调查的是( )
A.①②④ B.①③④ C.②③④ D.①②③
【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
解:①④中个体数量多,范围广,工作量大,不宜采用普查,只能采用抽样调查.③了解一批导弹的杀伤范围具有破坏性不宜普查.②个体数量少,可采用普查方式进行调查,故选B.
11.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(大于等于60)的有12人
【分析】根据频数分布直方图提供的信息,逐项进行判断即可.
解:由频数分布直方图可知:
A.得分在70~80分的人数最多,因此选项A正确;
B.该班的总人数为4+12+14+8+2=40(人),因此选项B正确;
C.人数最少的得分段的频数为2,因此选项C正确;
D.得分及格(≥60)的有12+14+8+2=36人,因此选项D错误;
故选:D.
12.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将(1)×2+(2)×3
B.要消去x,可以将(1)×3+(2)×(﹣5)
C.要消去y,可以将(1)×5+(2)×3
D.要消去x,可以将(1)×(﹣5)+(2)×3
【分析】观察方程组中x与y的系数特点,利用加减消元法判断即可.
解:利用加减消元法解方程组,做法正确的是要消去x,可以将(1)×(﹣5)+(2)×3,
故选:D.
13.如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地的方位角是北偏东43°,那么从C地测B地的方位角是( )
A.南偏东47° B.南偏西43° C.北偏东43° D.北偏西47°
【分析】根据方向角的概念和平行线的性质求解,即可得出从C地测B地的方位角.
解:∵AF∥DE,
∴∠ABE=∠FAB=43°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠CBD=47°,
∵BD∥CG,
∴∠BCG=47°,
∴从C地测B地的方位角是南偏东47°.
故选:A.
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
【分析】观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,分别得出点P运动的纵坐标的规律,再根据循环规律可得答案.
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
二、填空题(本大题共3个小题,每空3分,共12分)
15.1的平方根是 ±1 .
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:∵(±1)2=1,
∴1的平方根是±1.
故填±1.
16.若是关于x,y的二元一次方程﹣x+ay=3的解,则a= ﹣2 .
【分析】将代入二元一次方程﹣x+ay=3即可求得a的值.
解:将代入二元一次方程﹣x+ay=3得:
﹣1+a×(﹣2)=3.
∴a=﹣2.
故答案为:﹣2.
17.对于实数x,y规定“x△y=ax﹣by(a,b为常数)”.已知2△3=4,5△(﹣3)=3.
(1)a+b= .
(2)已知m是实数,若2△(﹣m)≥0,则m的最大值是 3 .
【分析】(1)根据已知条件得出关于a、b的方程组,求出方程组的解集即可;
(2)根据已知新运算得出2﹣m≥0,再解不等式即可.
解:(1)∵2△3=4,5△(﹣3)=3,
∴,
解得:,
∴a+b=,
故答案为;
(2)∵2△(﹣m)≥0,
∴2﹣m≥0,
∴m≤3,
∴m的最大值是3,
故答案为3.
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的解题步骤或文字说明)
18.对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果…那么…”的形式;
(2)判断此命题是真命题还是假命题.
【分析】(1)区分开条件和结论,改写成“如果…那么…”的形式即可;
(2)根据直角的定义进行判断即可.
解:(1)命题“相等的角是直角”的条件是两个角是相等;结论是这两个角是直角,
改写成“如果…那么…”的形式为:如果两个角相等,那么这两个角都是直角;
(2)“相等的角是直角”是假命题.
19.这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系.
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
【分析】(1)根据大门和花坛的坐标可建立平面直角坐标系;
(2)根据点A(3,1)即可确定A的位置.
解:(1)建立的平面直角坐标系如图所示,
(2)如图所示,点A即为所求.
20.新冠肺炎疫情爆发以来,党中央高度重视,带领全国人民众志成城,严防严控,以惊人的速度取得了阶段性胜利.某市教育主管部门响应上级号召,在初中生中开展了“新冠病毒预防知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(均为整数,总分100分),绘制了如图尚不完的统计图表.
调查结果统计表:
组别 成绩分组(单位:分) 频数
A 80≤x<85 50
B 85≤x<90 75
C 90≤x<95 150
D 95≤x≤100 a
合计
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量是 500 .
(2)统计表中,a= 225 .
(3)扇形统计图中,m的值为 45 ,“C”所对应的圆心角的度数为 108° ;
(4)若参加本次知识竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
【分析】(1)由A组频数及所占百分比即可求得样本容量
(2)根据各组频数之和等于总数求得a;
(3)D组人数除以总人数得出其百分比即可得m的值,再用360°乘C组所占百分比可得“C”所对应的圆心角的度数;
(4)总人数乘以样本中D组所占百分比即可.
解:(1)50÷0.1=500,
即样本容量是500.
故答案为:500;
(2)a=500﹣(50+75+150)=225.
故答案为:225;
(3)m%=×100%=45%,
∴m=45,
“C”所对应的圆心角的度数是360°×=108°,
故答案为:45,108°;
(4)5000×45%=2250(人),
答:估计成绩在95分及以上的学生大约有2250人.
21.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m2的正方形场地改建成300m2的长方形场地,且其长、宽的比为5:3.
(1)求原来正方形场地的周长.
(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.
【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;
(2)长、宽的比为5:3,设这个长方形场地宽为3am,则长为5am,计算出长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.
解:(1)(m),4×20=80(m),
答:原来正方形场地的周长为80m.
(2)设这个长方形场地宽为3am,则长为5am.
由题意有:3a×5a=300,
解得:,
∵3a表示长度,
∴a>0,
∴,
∴这个长方形场地的周长为 (m),
∵,
∴这些铁栅栏够用.
答:这些铁栅栏够用.
22.在平面直角坐标系中,点P的坐标为(a﹣7,3﹣2a),将点P向上平移4个单位,再向右平移5个单位后得到点Q.
(1)若点Q位于第一象限,求a的取值范围.
(2)若a为整数,求出P、Q两点坐标.
【分析】(1)依据点P向上平移4个单位,再向右平移5个单位后得到点Q(a﹣2,7﹣2a),点Q位于第一象限,即可得出a的取值范围.
(2)依据a为整数,2<a<3.5,即可得到a=3,进而得出P、Q两点坐标.
解:(1)∵点P的坐标为(a﹣7,3﹣2a),
∴将点P向上平移4个单位,再向右平移5个单位后得到点Q(a﹣2,7﹣2a),
∵点Q位于第一象限,
∴,
解得2<a<3.5.
(2)∵a为整数,2<a<3.5,
∴a=3,
∴P(﹣4,﹣3),Q(1,1).
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
【分析】(1)依据同位角相等两直线平行,得CE∥GF,由CE∥GF得∠C=∠FGD,再由∠C=∠EFG,得到∠FGD=∠EFG从而得到两直线平行;
(2)依据已知条件求得∠CGF的度数,根据平行线的性质可得角C的度数,进而得角AEC的度数,最后根据邻补角可得结论.
【解答】(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD;
(2)解:∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=∠GHD+∠D=80°+30°=110°,
又∵CE∥GF,
∴∠C+∠CGF=180°,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
24.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.
(1)求毛笔和宣纸的单价;
(2)某超市给出以下两种优惠方案:
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折.
学校准备购买毛笔50支,宣纸若干张(超过200张).选择哪种方案更划算?请说明理由.
【分析】(1)设毛笔的单价为x元,宣纸的单价为y元,根据“购买40支毛笔和100张宣纸需要28元;购买30支毛笔和200张宣纸需要260元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买宣纸m(m>200)张,利用总价=单价×数量,可找出选择方案A和选择方案B所需费用,分0.4m+280<0.32m+316,0.4m+280=0.32m+316和0.4m+280>0.32m+316三种情况,求出m的取值范围(或m的值)即可得出结论.
解:(1)设毛笔的单价为x元,宣纸的单价为y元,
依题意得:,
解得:.
答:毛笔的单价为6元,宣纸的单价为0.4元.
(2)设购买宣纸m(m>200)张.
选择方案A所需费用为50×6+0.4×(m﹣50)=0.4m+280(元);
选择方案B所需费用为50×6+0.4×200+0.4×0.8×(m﹣200)=0.32m+316.
当0.4m+280<0.32m+316时,解得:m<450,
∴当200<m<450时,选择方案A更划算;
当0.4m+280=0.32m+316时,解得:m=450,
∴当m=450时,选择方案A和方案B所需费用一样;
当0.4m+280>0.32m+316时,解得:m>450,
∴当m>450时,选择方案B更划算.
答:当购买的宣纸数量超过200张不足450张时,选择方案A更划算;当购买的宣纸数量等于450张时,选择两方案所需费用相同;当购买的宣纸数量超过450张时,选择方案B更划算.
一、选择题(共14个小题,每小题3分,共42分.)
1.实数是( )
A.分数 B.无理数 C.有理数 D.整数
2.如图,在一张透明的纸上画一条直线l,在l外任取一点Q并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
3.在平面直角坐标系中,点A(0,﹣2)在( )
A.x轴的负半轴上 B.y轴的负半轴上
C.x轴的正半轴上 D.y轴的正半轴上
4.用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
5.为了了解邢台市老年人的健康状况,在以下的抽样调查中,你认为样本选择较合适的是( )
A.在达活泉晨练的100位老人
B.到邢台人民医院随机抽查的100位住院老人
C.到某养老院随机抽查的100位老人
D.从全市户籍管理系统任意抽取100位老人
6.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
7.将一块体积为64cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )
A.2cm B.3cm C.4cm D.5cm
8.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
9.如图,表示实数(1﹣)的点落在( )
A.段① B.段② C.段③ D.段④
10.下列调查:①了解夏季冷饮市场上冰淇淋的质量;②了解李红同学60道英语选择题的通过率;③了解一批导弹的杀伤范围;④了解全世界网迷少年的性格情况.不适合普查而适合做抽样调查的是( )
A.①②④ B.①③④ C.②③④ D.①②③
11.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(大于等于60)的有12人
12.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将(1)×2+(2)×3
B.要消去x,可以将(1)×3+(2)×(﹣5)
C.要消去y,可以将(1)×5+(2)×3
D.要消去x,可以将(1)×(﹣5)+(2)×3
13.如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地的方位角是北偏东43°,那么从C地测B地的方位角是( )
A.南偏东47° B.南偏西43° C.北偏东43° D.北偏西47°
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
二、填空题(本大题共3个小题,每空3分,共12分)
15.1的平方根是 .
16.若是关于x,y的二元一次方程﹣x+ay=3的解,则a= .
17.对于实数x,y规定“x△y=ax﹣by(a,b为常数)”.已知2△3=4,5△(﹣3)=3.
(1)a+b= .
(2)已知m是实数,若2△(﹣m)≥0,则m的最大值是 .
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的解题步骤或文字说明)
18.对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果…那么…”的形式;
(2)判断此命题是真命题还是假命题.
19.这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系.
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
20.新冠肺炎疫情爆发以来,党中央高度重视,带领全国人民众志成城,严防严控,以惊人的速度取得了阶段性胜利.某市教育主管部门响应上级号召,在初中生中开展了“新冠病毒预防知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(均为整数,总分100分),绘制了如图尚不完的统计图表.
调查结果统计表:
组别 成绩分组(单位:分) 频数
A 80≤x<85 50
B 85≤x<90 75
C 90≤x<95 150
D 95≤x≤100 a
合计
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量是 .
(2)统计表中,a= .
(3)扇形统计图中,m的值为 ,“C”所对应的圆心角的度数为 ;
(4)若参加本次知识竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
21.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m2的正方形场地改建成300m2的长方形场地,且其长、宽的比为5:3.
(1)求原来正方形场地的周长.
(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.
22.在平面直角坐标系中,点P的坐标为(a﹣7,3﹣2a),将点P向上平移4个单位,再向右平移5个单位后得到点Q.
(1)若点Q位于第一象限,求a的取值范围.
(2)若a为整数,求出P、Q两点坐标.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.
(1)求毛笔和宣纸的单价;
(2)某超市给出以下两种优惠方案:
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折.
学校准备购买毛笔50支,宣纸若干张(超过200张).选择哪种方案更划算?请说明理由.
参考答案
一、选择题(本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.实数是( )
A.分数 B.无理数 C.有理数 D.整数
【分析】根据无理数的定义即可判断.
解:∵是无限不循环小数,
∴是无理数,
∴是无理数,
故选:B.
2.如图,在一张透明的纸上画一条直线l,在l外任取一点Q并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
【分析】根据垂线的基本性质:过直线上或直线外的一点,有且只有一条直线和已知直线垂直,容易判断.
解:根据垂线的性质,这样的直线只能作一条,
故选:B.
3.在平面直角坐标系中,点A(0,﹣2)在( )
A.x轴的负半轴上 B.y轴的负半轴上
C.x轴的正半轴上 D.y轴的正半轴上
【分析】根据y轴上的横坐标等于零,y轴上纵坐标小于零的点在y轴的负半轴上,可得答案.
解:在平面直角坐标系中,点A(0,﹣2)在y轴的负半轴上,
故选:B.
4.用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
【分析】不等式的解集在数轴上表示出来的方法:“>”空心圆点向右画折线,“≥”实心圆点向右画折线,“<”空心圆点向左画折线,“≤”实心圆点向左画折线.
解:本题可观察数轴向右画又是实心圆,因此是x≥﹣2.
故选:C.
5.为了了解邢台市老年人的健康状况,在以下的抽样调查中,你认为样本选择较合适的是( )
A.在达活泉晨练的100位老人
B.到邢台人民医院随机抽查的100位住院老人
C.到某养老院随机抽查的100位老人
D.从全市户籍管理系统任意抽取100位老人
【分析】根据抽取样本的代表性、可靠性,结合具体的情景进行判断即可.
解:A.在达活泉晨练的100位老人,不具有代表性,所得结果的可靠性不高,因此选项A不符合题意;
B.到邢台人民医院随机抽查的100位住院老人,这样所得的结果具有片面性,可靠性不高,因此选项B不符合题意;
C.到某养老院随机抽查的100位老人,不具有代表性,所得结果的可靠性不高,因此选项C不符合题意;
D.从全市户籍管理系统任意抽取100位老人,这样取样具有代表性,广泛性,可靠性较强,因此选项D符合题意;
故选:D.
6.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是C.
解:观察图形可知图案C通过平移后可以得到.
故选:C.
7.将一块体积为64cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )
A.2cm B.3cm C.4cm D.5cm
【分析】利用立方根定义求出棱长即可.
解:根据题意知,每个小正方体木块的棱长为==2(cm),
故选:A.
8.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
【分析】根据各选项的表述列出个不等式,与选项中所表示的比对即可得出答案.
【解答】A、a不是负数,可表示成a≥0,故本选项错误;
B、x不大于3,可表示成x≤3,故本选项错误;
C、m与4的差是负数,可表示成m﹣4<0,故本选项正确;
D、x与2的和是非负数,可表示成x+2≥0,故本选项错误.
故选:C.
9.如图,表示实数(1﹣)的点落在( )
A.段① B.段② C.段③ D.段④
【分析】先确定的近似值,然后求出1﹣的值,再对应数轴上的每一段范围即可确定答案.
解:∵≈1.732…,
∴1﹣≈﹣0.732…,
∵段③的范围是﹣1~0,
∴表示(1﹣)的点落在段③.
故选:C.
10.下列调查:①了解夏季冷饮市场上冰淇淋的质量;②了解李红同学60道英语选择题的通过率;③了解一批导弹的杀伤范围;④了解全世界网迷少年的性格情况.不适合普查而适合做抽样调查的是( )
A.①②④ B.①③④ C.②③④ D.①②③
【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
解:①④中个体数量多,范围广,工作量大,不宜采用普查,只能采用抽样调查.③了解一批导弹的杀伤范围具有破坏性不宜普查.②个体数量少,可采用普查方式进行调查,故选B.
11.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(大于等于60)的有12人
【分析】根据频数分布直方图提供的信息,逐项进行判断即可.
解:由频数分布直方图可知:
A.得分在70~80分的人数最多,因此选项A正确;
B.该班的总人数为4+12+14+8+2=40(人),因此选项B正确;
C.人数最少的得分段的频数为2,因此选项C正确;
D.得分及格(≥60)的有12+14+8+2=36人,因此选项D错误;
故选:D.
12.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将(1)×2+(2)×3
B.要消去x,可以将(1)×3+(2)×(﹣5)
C.要消去y,可以将(1)×5+(2)×3
D.要消去x,可以将(1)×(﹣5)+(2)×3
【分析】观察方程组中x与y的系数特点,利用加减消元法判断即可.
解:利用加减消元法解方程组,做法正确的是要消去x,可以将(1)×(﹣5)+(2)×3,
故选:D.
13.如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地的方位角是北偏东43°,那么从C地测B地的方位角是( )
A.南偏东47° B.南偏西43° C.北偏东43° D.北偏西47°
【分析】根据方向角的概念和平行线的性质求解,即可得出从C地测B地的方位角.
解:∵AF∥DE,
∴∠ABE=∠FAB=43°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠CBD=47°,
∵BD∥CG,
∴∠BCG=47°,
∴从C地测B地的方位角是南偏东47°.
故选:A.
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
【分析】观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,分别得出点P运动的纵坐标的规律,再根据循环规律可得答案.
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
二、填空题(本大题共3个小题,每空3分,共12分)
15.1的平方根是 ±1 .
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:∵(±1)2=1,
∴1的平方根是±1.
故填±1.
16.若是关于x,y的二元一次方程﹣x+ay=3的解,则a= ﹣2 .
【分析】将代入二元一次方程﹣x+ay=3即可求得a的值.
解:将代入二元一次方程﹣x+ay=3得:
﹣1+a×(﹣2)=3.
∴a=﹣2.
故答案为:﹣2.
17.对于实数x,y规定“x△y=ax﹣by(a,b为常数)”.已知2△3=4,5△(﹣3)=3.
(1)a+b= .
(2)已知m是实数,若2△(﹣m)≥0,则m的最大值是 3 .
【分析】(1)根据已知条件得出关于a、b的方程组,求出方程组的解集即可;
(2)根据已知新运算得出2﹣m≥0,再解不等式即可.
解:(1)∵2△3=4,5△(﹣3)=3,
∴,
解得:,
∴a+b=,
故答案为;
(2)∵2△(﹣m)≥0,
∴2﹣m≥0,
∴m≤3,
∴m的最大值是3,
故答案为3.
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的解题步骤或文字说明)
18.对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果…那么…”的形式;
(2)判断此命题是真命题还是假命题.
【分析】(1)区分开条件和结论,改写成“如果…那么…”的形式即可;
(2)根据直角的定义进行判断即可.
解:(1)命题“相等的角是直角”的条件是两个角是相等;结论是这两个角是直角,
改写成“如果…那么…”的形式为:如果两个角相等,那么这两个角都是直角;
(2)“相等的角是直角”是假命题.
19.这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系.
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
【分析】(1)根据大门和花坛的坐标可建立平面直角坐标系;
(2)根据点A(3,1)即可确定A的位置.
解:(1)建立的平面直角坐标系如图所示,
(2)如图所示,点A即为所求.
20.新冠肺炎疫情爆发以来,党中央高度重视,带领全国人民众志成城,严防严控,以惊人的速度取得了阶段性胜利.某市教育主管部门响应上级号召,在初中生中开展了“新冠病毒预防知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(均为整数,总分100分),绘制了如图尚不完的统计图表.
调查结果统计表:
组别 成绩分组(单位:分) 频数
A 80≤x<85 50
B 85≤x<90 75
C 90≤x<95 150
D 95≤x≤100 a
合计
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量是 500 .
(2)统计表中,a= 225 .
(3)扇形统计图中,m的值为 45 ,“C”所对应的圆心角的度数为 108° ;
(4)若参加本次知识竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
【分析】(1)由A组频数及所占百分比即可求得样本容量
(2)根据各组频数之和等于总数求得a;
(3)D组人数除以总人数得出其百分比即可得m的值,再用360°乘C组所占百分比可得“C”所对应的圆心角的度数;
(4)总人数乘以样本中D组所占百分比即可.
解:(1)50÷0.1=500,
即样本容量是500.
故答案为:500;
(2)a=500﹣(50+75+150)=225.
故答案为:225;
(3)m%=×100%=45%,
∴m=45,
“C”所对应的圆心角的度数是360°×=108°,
故答案为:45,108°;
(4)5000×45%=2250(人),
答:估计成绩在95分及以上的学生大约有2250人.
21.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m2的正方形场地改建成300m2的长方形场地,且其长、宽的比为5:3.
(1)求原来正方形场地的周长.
(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.
【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;
(2)长、宽的比为5:3,设这个长方形场地宽为3am,则长为5am,计算出长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.
解:(1)(m),4×20=80(m),
答:原来正方形场地的周长为80m.
(2)设这个长方形场地宽为3am,则长为5am.
由题意有:3a×5a=300,
解得:,
∵3a表示长度,
∴a>0,
∴,
∴这个长方形场地的周长为 (m),
∵,
∴这些铁栅栏够用.
答:这些铁栅栏够用.
22.在平面直角坐标系中,点P的坐标为(a﹣7,3﹣2a),将点P向上平移4个单位,再向右平移5个单位后得到点Q.
(1)若点Q位于第一象限,求a的取值范围.
(2)若a为整数,求出P、Q两点坐标.
【分析】(1)依据点P向上平移4个单位,再向右平移5个单位后得到点Q(a﹣2,7﹣2a),点Q位于第一象限,即可得出a的取值范围.
(2)依据a为整数,2<a<3.5,即可得到a=3,进而得出P、Q两点坐标.
解:(1)∵点P的坐标为(a﹣7,3﹣2a),
∴将点P向上平移4个单位,再向右平移5个单位后得到点Q(a﹣2,7﹣2a),
∵点Q位于第一象限,
∴,
解得2<a<3.5.
(2)∵a为整数,2<a<3.5,
∴a=3,
∴P(﹣4,﹣3),Q(1,1).
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
【分析】(1)依据同位角相等两直线平行,得CE∥GF,由CE∥GF得∠C=∠FGD,再由∠C=∠EFG,得到∠FGD=∠EFG从而得到两直线平行;
(2)依据已知条件求得∠CGF的度数,根据平行线的性质可得角C的度数,进而得角AEC的度数,最后根据邻补角可得结论.
【解答】(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD;
(2)解:∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=∠GHD+∠D=80°+30°=110°,
又∵CE∥GF,
∴∠C+∠CGF=180°,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
24.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.
(1)求毛笔和宣纸的单价;
(2)某超市给出以下两种优惠方案:
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折.
学校准备购买毛笔50支,宣纸若干张(超过200张).选择哪种方案更划算?请说明理由.
【分析】(1)设毛笔的单价为x元,宣纸的单价为y元,根据“购买40支毛笔和100张宣纸需要28元;购买30支毛笔和200张宣纸需要260元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买宣纸m(m>200)张,利用总价=单价×数量,可找出选择方案A和选择方案B所需费用,分0.4m+280<0.32m+316,0.4m+280=0.32m+316和0.4m+280>0.32m+316三种情况,求出m的取值范围(或m的值)即可得出结论.
解:(1)设毛笔的单价为x元,宣纸的单价为y元,
依题意得:,
解得:.
答:毛笔的单价为6元,宣纸的单价为0.4元.
(2)设购买宣纸m(m>200)张.
选择方案A所需费用为50×6+0.4×(m﹣50)=0.4m+280(元);
选择方案B所需费用为50×6+0.4×200+0.4×0.8×(m﹣200)=0.32m+316.
当0.4m+280<0.32m+316时,解得:m<450,
∴当200<m<450时,选择方案A更划算;
当0.4m+280=0.32m+316时,解得:m=450,
∴当m=450时,选择方案A和方案B所需费用一样;
当0.4m+280>0.32m+316时,解得:m>450,
∴当m>450时,选择方案B更划算.
答:当购买的宣纸数量超过200张不足450张时,选择方案A更划算;当购买的宣纸数量等于450张时,选择两方案所需费用相同;当购买的宣纸数量超过450张时,选择方案B更划算.
同课章节目录
