8.2.2 条件概率教案-湘教版数学选修2-3(Word版)
文档属性
| 名称 | 8.2.2 条件概率教案-湘教版数学选修2-3(Word版) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:00:57 | ||
图片预览


文档简介
条 件 概 率
一、教材分析
概率一章自成体系,是数学中一个较独立的学科分支,与以往所学的数学知识有很大区别,但与人们的日常生活密切相关,而且对思维能力有较高要求,在高考中占有重要地位。本节内容在教材中起着承前启后的作用,一可以巩固古典概型的概率计算方法,二为研究相互独立事件打下良好基础。
二、学情分析
为了体现以生为本,遵循学生的认知规律,坚持以教师为主导,学生为主体的教学思想,体现循序渐进的教学原则,我采用引导发现法、分析讨论法的教学方法,通过提问、启发、设问、归纳、讲练结合、适时点拨的方法,让学生的思维活动在老师的引导下层层展开让学生大胆参与课堂教学。
课时分配
1课时
三、教学目标
1.知识与技能
通过对具体情境的分析,了解条件概率的定义,掌握简单的条件概率的计算.
2.过程与方法
发展抽象、概括能力,提高解决实际问题的能力.
3.情感、态度与价值观
使学生了解数学来源于实际,应用于实际的唯物主义思想.
四、教学重点、难点
教学重点:条件概率定义的理解.
教学难点:概率计算公式的应用.
五、教学过程
1.复习引入:
事件概率加法公式:
注:
1.事件A与B至少有一个发生的事件叫做A与B的
和事件,记为false(或false);
2.事件A与B都发生的事件叫做A与B的积事件,记为false (或false );
3.若 false为不可能事件,则说事件A与B互斥.
2. 创设情境,引出定义:
探究: 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两名同学小。(由学生分组讨论,得出正确答案)
问题1:如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到奖券的概率又是多少?
问题2:已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
设计意图:让学生感受由浅到深,从感性到理性的发生过程,进而引出条件概率定义。
引出定义:对于任何两个事件A和B,在已知事件A发生的条件下,事件B发生的概率叫条件概率。
用false表示三名同学可能抽取的结果全体,则它由三个基本事件组成,即false={Yfalsefalse, falseYfalse,falsefalseY}。既然已知事件A必然发生,那么只需在A={falseYfalse, falsefalseY}的范围内考虑问题,即只有两个基本事件falseYfalse和falsefalseY.在事件 A 发生的情况下事件B发生,等价于事件 A 和事件 B 同时发生,即 AB 发生。而事件 AB 中仅含一个基本事件falsefalseY,因此false=false=false 。其中n ( A)和 n ( AB)分别表示事件 A 和事件 AB 所包含的基本事件个数。另一方面,根据古典概型的计算公式, false
其中 n(false)表示false中包含的基本事件个数。所以,false=false。
因此,可以通过事件A和事件AB的概率来表示P(B| A ) 。false 。
由这个定义可知,对任意两个事件A、B,若false,则有false。
并称上式为概率的乘法公式。
一般地,在已知另一事件A发生的前提下,事件B发生的可能性大小不一定再是P(B).即
false条件的附加意味着对样本空间进行压缩.
引例:
掷红、蓝两颗骰子,设事件A=“蓝色骰子的点数为3或6”
事件B=“两颗骰子点数之和大于8”
求(1)P(A),P(B),P(AB)
(2)在“事件A已发生”的附加条件下事件B发生的概率?
(3)比较(2)中结果与P(AB)的大小及三者概率之间关系
(这个例题可让学生模仿上个例题,自己写步骤,可让学生到黑板上去写)
设计意图:进一步使学生加深对条件概率定义的理解和条件概率公式计算的运用。
思 考
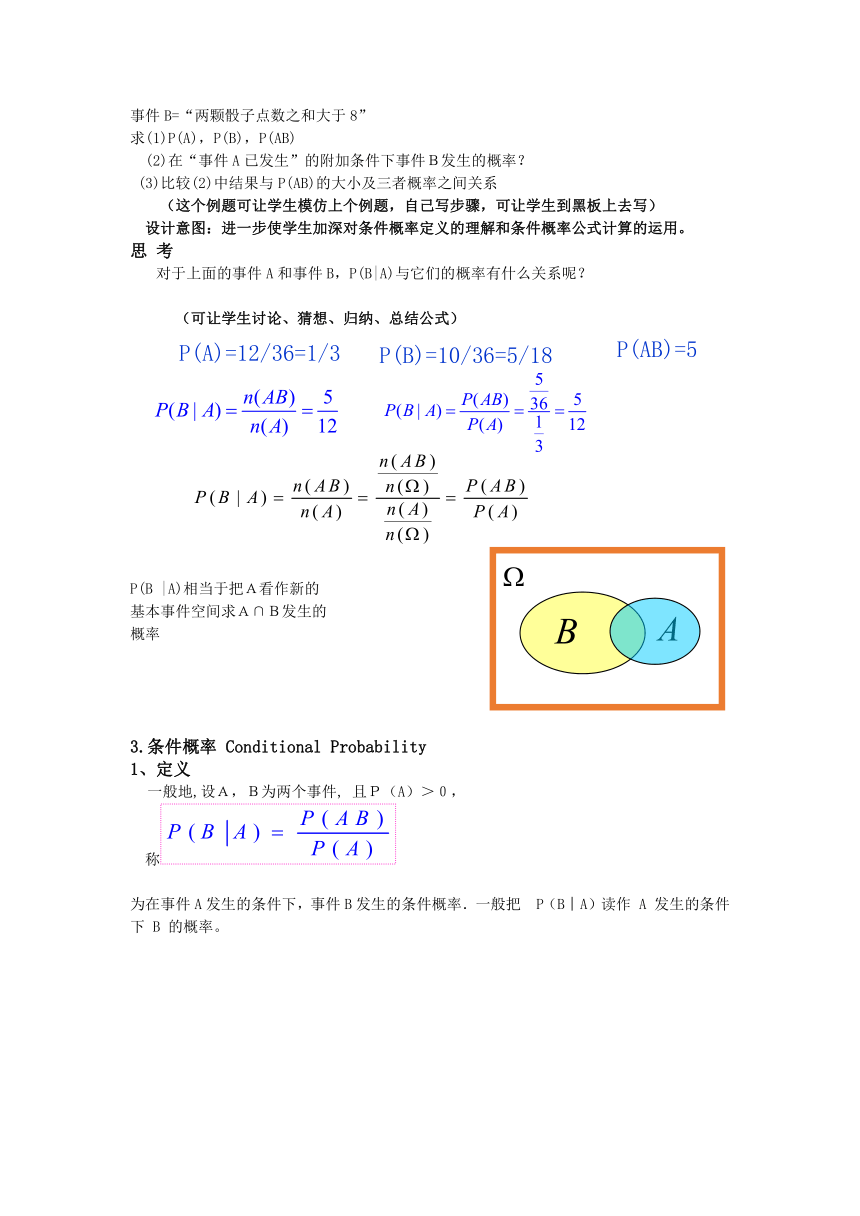
对于上面的事件A和事件B,P(B|A)与它们的概率有什么关系呢?
-10160155575P(A)=12/36=1/3
P(A)=12/36=1/3
3914775121920P(AB)=5/36
P(AB)=5/36
1731010174625P(B)=10/36=5/18
P(B)=10/36=5/18
(可让学生讨论、猜想、归纳、总结公式)
2210435137160
18859585090
3190240951865 false
324612049530
42202101854203429000131445P(B |A)相当于把A看作新的
458787572390369062083820基本事件空间求A∩B发生的
概率
3.条件概率 Conditional Probability
1、定义
一般地,设A,B为两个事件, 且P(A)>0,
称false
为在事件A发生的条件下,事件B发生的条件概率.一般把 P(B︱A)读作 A 发生的条件下 B 的概率。
4.例题1:在某次外交谈判中,中外双方都为了自身的利益而互不相让,这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理,否则按中方的决议处理,假如你在现场,你会如何抉择?
解1:设A={出现的点数不超过3}={1,2,3}
B={出现的点数是奇数} ={1,3,5}
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
313690163195
41148031750106680089535
996315679451
3
1
3
3822701174751928495149860
419100552455
5
17932401771652
2
4178303562354,6
4,6
条件概率计算中注意的问题
1、条件概率的判断:
(1)当题目中出现“在……前提(条件)下”等字眼,一般为条件概率。
(2)当已知事件的发生影响所求事件的概率,一般也认为是条件概率。
2、相应事件的判断:
首先用相应的字母A、B表示出相应的事件,然后分析清楚在哪个事件发生的条件下求哪个事件的概率。false
5.反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
(3)利用条件概率公式求
19050769620练一练
练一练
false
设计意图:通过练习,让学生进一步巩固,掌握条件概率的求法。
1.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则falsefalse
254952553022544767505505450.7
0.7
27222455346702476500438150所求概率为 false
31432501371600.56false
0.56false
320675066040
4873625153670
2601595266705
5
2.全年级100名学生中,有男生(以事件A表示)80人,女生20人; 来自北京的(以事件B表示)有20人,其中男生12人,女生8人;免修英语的(以事件C表示)40人中,有32名男生,8名女生。求
false
false false false false false
false
false false false false
3.一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求 (1) 第一次取得白球的概率; (2) 第一、第二次都取得白球的概率; (3) 第一次取得黑球而第二次取得白球的概率.
解
设A表示第一次取得白球, B表示第二次取得白球, 则
-167005153670(1)
(1)
671195163830
-171450165735(2)
(2)
2682875161290
61912597155126492040640
9461585090(3)
(3)
2893695102870
61595012700
4.设n件产品中含有m件废品,今从中任取两件,在已知其中一件是废品的前提下,求另一件也是废品的概率。
6.课堂小结
1. 条件概率的定义.
2. 条件概率的计算.
公式:
false
2.概率P(B|A)与P(AB)的区别与联系:
P(AB)表示在样本空间Ω中,计算AB发生的概率,而P(B|A)表示在缩小的样本空间ΩA中,计算B发生的概率.用古典概率公式,则P(B|A)=,P(AB)=.
六、【作业】
1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为n(Ω)=A=20.
根据分步乘法计数原理,n(A)=A×A=12.于是P(A)===.
(2)因为n(AB)=A=6,所以P(AB)===.
(3)解法1:由(1)(2)可得,在“第1次抽到理科题的条件下,第2次抽到理科题”的概率为P(B|A)===.
解法2:因为n(AB)=6,n(A)=12,所以P(B|A)===.
2.一个袋中装有2个黑球和3个白球,如果不放回地抽取两个球,记事件“第一次抽到白球”为A;事件“第二次抽到白球”为B.
(1)分别求事件A、B、AB发生的概率;
(2)求P(B|A).
解:同2.
七、板书设计:
条件概率
引入:
探究性题目:
问题1
问题2
二、定义:
题组练习:
问题3
三、公式推导:
四、典型例题:
例1
例2
五、课堂练习:
(1)
(2)
(3)
六、小结:
七、布置作业:
八、教学反思与自我评价
好的教学情境的创设,等于成功的一半.因而,以一个轻松愉快的抽奖券游戏把学生带进一个轻松愉快的课堂环境中.从游戏开始,诱思深入,把老师在堂上讲、学生在堂下听的教学过程变为师生共同探索,共同研究的过程.学生围绕老师提出的一系列具有趣味性和启发性的层层深入的问题,展开讨论,使问题得到解决,从而突出本节重点,突破本节难点.
6370955113665P(AB)=5/36
P(AB)=5/36
一、教材分析
概率一章自成体系,是数学中一个较独立的学科分支,与以往所学的数学知识有很大区别,但与人们的日常生活密切相关,而且对思维能力有较高要求,在高考中占有重要地位。本节内容在教材中起着承前启后的作用,一可以巩固古典概型的概率计算方法,二为研究相互独立事件打下良好基础。
二、学情分析
为了体现以生为本,遵循学生的认知规律,坚持以教师为主导,学生为主体的教学思想,体现循序渐进的教学原则,我采用引导发现法、分析讨论法的教学方法,通过提问、启发、设问、归纳、讲练结合、适时点拨的方法,让学生的思维活动在老师的引导下层层展开让学生大胆参与课堂教学。
课时分配
1课时
三、教学目标
1.知识与技能
通过对具体情境的分析,了解条件概率的定义,掌握简单的条件概率的计算.
2.过程与方法
发展抽象、概括能力,提高解决实际问题的能力.
3.情感、态度与价值观
使学生了解数学来源于实际,应用于实际的唯物主义思想.
四、教学重点、难点
教学重点:条件概率定义的理解.
教学难点:概率计算公式的应用.
五、教学过程
1.复习引入:
事件概率加法公式:
注:
1.事件A与B至少有一个发生的事件叫做A与B的
和事件,记为false(或false);
2.事件A与B都发生的事件叫做A与B的积事件,记为false (或false );
3.若 false为不可能事件,则说事件A与B互斥.
2. 创设情境,引出定义:
探究: 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两名同学小。(由学生分组讨论,得出正确答案)
问题1:如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到奖券的概率又是多少?
问题2:已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
设计意图:让学生感受由浅到深,从感性到理性的发生过程,进而引出条件概率定义。
引出定义:对于任何两个事件A和B,在已知事件A发生的条件下,事件B发生的概率叫条件概率。
用false表示三名同学可能抽取的结果全体,则它由三个基本事件组成,即false={Yfalsefalse, falseYfalse,falsefalseY}。既然已知事件A必然发生,那么只需在A={falseYfalse, falsefalseY}的范围内考虑问题,即只有两个基本事件falseYfalse和falsefalseY.在事件 A 发生的情况下事件B发生,等价于事件 A 和事件 B 同时发生,即 AB 发生。而事件 AB 中仅含一个基本事件falsefalseY,因此false=false=false 。其中n ( A)和 n ( AB)分别表示事件 A 和事件 AB 所包含的基本事件个数。另一方面,根据古典概型的计算公式, false
其中 n(false)表示false中包含的基本事件个数。所以,false=false。
因此,可以通过事件A和事件AB的概率来表示P(B| A ) 。false 。
由这个定义可知,对任意两个事件A、B,若false,则有false。
并称上式为概率的乘法公式。
一般地,在已知另一事件A发生的前提下,事件B发生的可能性大小不一定再是P(B).即
false条件的附加意味着对样本空间进行压缩.
引例:
掷红、蓝两颗骰子,设事件A=“蓝色骰子的点数为3或6”
事件B=“两颗骰子点数之和大于8”
求(1)P(A),P(B),P(AB)
(2)在“事件A已发生”的附加条件下事件B发生的概率?
(3)比较(2)中结果与P(AB)的大小及三者概率之间关系
(这个例题可让学生模仿上个例题,自己写步骤,可让学生到黑板上去写)
设计意图:进一步使学生加深对条件概率定义的理解和条件概率公式计算的运用。
思 考
对于上面的事件A和事件B,P(B|A)与它们的概率有什么关系呢?
-10160155575P(A)=12/36=1/3
P(A)=12/36=1/3
3914775121920P(AB)=5/36
P(AB)=5/36
1731010174625P(B)=10/36=5/18
P(B)=10/36=5/18
(可让学生讨论、猜想、归纳、总结公式)
2210435137160
18859585090
3190240951865 false
324612049530
42202101854203429000131445P(B |A)相当于把A看作新的
458787572390369062083820基本事件空间求A∩B发生的
概率
3.条件概率 Conditional Probability
1、定义
一般地,设A,B为两个事件, 且P(A)>0,
称false
为在事件A发生的条件下,事件B发生的条件概率.一般把 P(B︱A)读作 A 发生的条件下 B 的概率。
4.例题1:在某次外交谈判中,中外双方都为了自身的利益而互不相让,这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理,否则按中方的决议处理,假如你在现场,你会如何抉择?
解1:设A={出现的点数不超过3}={1,2,3}
B={出现的点数是奇数} ={1,3,5}
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
313690163195
41148031750106680089535
996315679451
3
1
3
3822701174751928495149860
419100552455
5
17932401771652
2
4178303562354,6
4,6
条件概率计算中注意的问题
1、条件概率的判断:
(1)当题目中出现“在……前提(条件)下”等字眼,一般为条件概率。
(2)当已知事件的发生影响所求事件的概率,一般也认为是条件概率。
2、相应事件的判断:
首先用相应的字母A、B表示出相应的事件,然后分析清楚在哪个事件发生的条件下求哪个事件的概率。false
5.反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
(3)利用条件概率公式求
19050769620练一练
练一练
false
设计意图:通过练习,让学生进一步巩固,掌握条件概率的求法。
1.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则falsefalse
254952553022544767505505450.7
0.7
27222455346702476500438150所求概率为 false
31432501371600.56false
0.56false
320675066040
4873625153670
2601595266705
5
2.全年级100名学生中,有男生(以事件A表示)80人,女生20人; 来自北京的(以事件B表示)有20人,其中男生12人,女生8人;免修英语的(以事件C表示)40人中,有32名男生,8名女生。求
false
false false false false false
false
false false false false
3.一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求 (1) 第一次取得白球的概率; (2) 第一、第二次都取得白球的概率; (3) 第一次取得黑球而第二次取得白球的概率.
解
设A表示第一次取得白球, B表示第二次取得白球, 则
-167005153670(1)
(1)
671195163830
-171450165735(2)
(2)
2682875161290
61912597155126492040640
9461585090(3)
(3)
2893695102870
61595012700
4.设n件产品中含有m件废品,今从中任取两件,在已知其中一件是废品的前提下,求另一件也是废品的概率。
6.课堂小结
1. 条件概率的定义.
2. 条件概率的计算.
公式:
false
2.概率P(B|A)与P(AB)的区别与联系:
P(AB)表示在样本空间Ω中,计算AB发生的概率,而P(B|A)表示在缩小的样本空间ΩA中,计算B发生的概率.用古典概率公式,则P(B|A)=,P(AB)=.
六、【作业】
1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为n(Ω)=A=20.
根据分步乘法计数原理,n(A)=A×A=12.于是P(A)===.
(2)因为n(AB)=A=6,所以P(AB)===.
(3)解法1:由(1)(2)可得,在“第1次抽到理科题的条件下,第2次抽到理科题”的概率为P(B|A)===.
解法2:因为n(AB)=6,n(A)=12,所以P(B|A)===.
2.一个袋中装有2个黑球和3个白球,如果不放回地抽取两个球,记事件“第一次抽到白球”为A;事件“第二次抽到白球”为B.
(1)分别求事件A、B、AB发生的概率;
(2)求P(B|A).
解:同2.
七、板书设计:
条件概率
引入:
探究性题目:
问题1
问题2
二、定义:
题组练习:
问题3
三、公式推导:
四、典型例题:
例1
例2
五、课堂练习:
(1)
(2)
(3)
六、小结:
七、布置作业:
八、教学反思与自我评价
好的教学情境的创设,等于成功的一半.因而,以一个轻松愉快的抽奖券游戏把学生带进一个轻松愉快的课堂环境中.从游戏开始,诱思深入,把老师在堂上讲、学生在堂下听的教学过程变为师生共同探索,共同研究的过程.学生围绕老师提出的一系列具有趣味性和启发性的层层深入的问题,展开讨论,使问题得到解决,从而突出本节重点,突破本节难点.
6370955113665P(AB)=5/36
P(AB)=5/36
同课章节目录
