8.5 一元线性回归案例(1)教案-湘教版数学选修2-3(Word版)
文档属性
| 名称 | 8.5 一元线性回归案例(1)教案-湘教版数学选修2-3(Word版) |

|
|
| 格式 | doc | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:12:48 | ||
图片预览



文档简介
8.5一元线性回归案例
湘教版选修2-3 第8.5节
【教学目标】
知识与技能
了解样本、样本容量、线性回归的概念,理解变量之间的相关系数的概念、相关系数、一元线性回归直线等概念。
过程与方法
熟练利用公式求相关系数,掌握求一元线性回归直线方程 的方法,加深理解线性回归模型的意义。判断变量间是否线性相关。
情感、态度与价值观
培养学生分析问题、解决问题的能力,收集数据和处理数据的能力。
【教材分析】
教学重点:让学生了解线性回归的基本思想和方法。
教学难点:掌握建立回归模型的基本步骤。
变量间的关系:
函数关系:自变量x确定y唯一确定;(确定关系)
相关关系:当自变量一定时,因变量的取值带有一定的随机性的两个变量之间的关系称为相关关系 。
例如:在水稻产量与施肥量的关系中,施肥量是可控制变量,而水稻产量是随机变量。因此只能说明水稻产量与施肥量是相关关系。
现实生活中相关关系大量存在,从某种意义上看,函数是一种理想的关系模型,而相关关系式一种更为一般的情况,因此更有研究相关关系的必要了。
一元线性回归分析
在具有相关关系的变量中如果因变量仅与一个变量有关,相应的统计分析成为一元回归分析;若与因变量与多个自变量有关,称为多元线性回归分析。
线性相关性检验:(相关系数检验法)
当 >0时,我们称其正相关;
当 <0时,我们称其负相关;
当 =0时,我们称其不相关。
教学过程 教师活动 学生活动 设计意图
引
入
新
知
问题一:如果有两个变量X和Y,那么这两个变量之间有什么关系呢?
(联系我们之前学过的知识,哪些涉及了两个变量并着重强调两个变量之间的关系呢?)
用身高和体重这个例子引出相关关系那么什么叫做相关关系呢?函数关系与相关关系之间又有什么异同点呢?
那么这节课我们就一起来研究一下相关关系。
答:
函数:涉及了两个变量,自变量X因变量Y,
随着自变量X的变化相应的有唯一的因变量Y与之对应
函数关系
相关关系
通过对两个变量之间关系的探讨,既复习了已学的函数知识,又引出这节课所要关注的相关关系。
讲
授
新
知
在此之前,我们先一起来看一道例题。
一、首先我们先一起分析一下表中所给数据,你能得到怎样的结论呢?
这是我们从表中数据直接得到的,一般情况下对于数据的处理我们除了可以采用列表法,还可以采用图像法。那么为了更加直观的反映整体走势,下面请同学们根据表中数据在坐标系中绘出相应各点。看看能得到什么样的结论呢?
(用excel绘制散点图)
我们发现绘制出的图形呈现一个一个的散点,我们称这样的图形为散点图。
并且从数据散点图看到有随着的增加而沿某
直线增加的趋势。并且这些散点是相对较均匀的分布在这条直线的两侧。那么这条直线就被我们叫做一元线性回归直线,
答:随着施化肥量的增加,产量Y也是在逐年增加的;并且产量Y整体呈现一种上升的趋势。
通过学生对数据的观察可以大概得到两个变量间的关系,但是未来更加直观便可以借助散点图来帮助我们分析。
讲
授
新
知
那么这条直线该如何确定呢?(为了解决确定直线的问题,我们先给出一些必要的公式。)
二、下面介绍一个新的名词定义——相关系数。
当 时,…………
我们称其为相关系数、并且相关系数有如下几条性质:
1、正相关、负相关和不相关;(主要根据90至91页的图形加以说明)
2、.相关系数的取值为[-1,1]
3、相关系数的大小与相关程度的关系。
从90页的六个散点图中,我们可以发现散点图的密集程度是不一样的,并且这种密集程度与相关系数有着一定的联系,相关系数越接近1,X,Y的线性相关性越强,并随着X的增加Y也在线性增加。
讲
授
新
知
讲
授
新
知 三、既然学习了相关系数,下面我们就一起来解决例1中的3个问题。
首先我们先一起来计算一下例一中两个变量X、Y的相关系数。
要计算相关系数,就要求解哪些量呢?
(我们发现很接近1,说明钢水的含碳量x与冶炼时间y 正相关,即随着X的增加Y也是在增加的。就此我们可以预测出钢水的含碳量x增加时,冶炼时间y也会增加。)
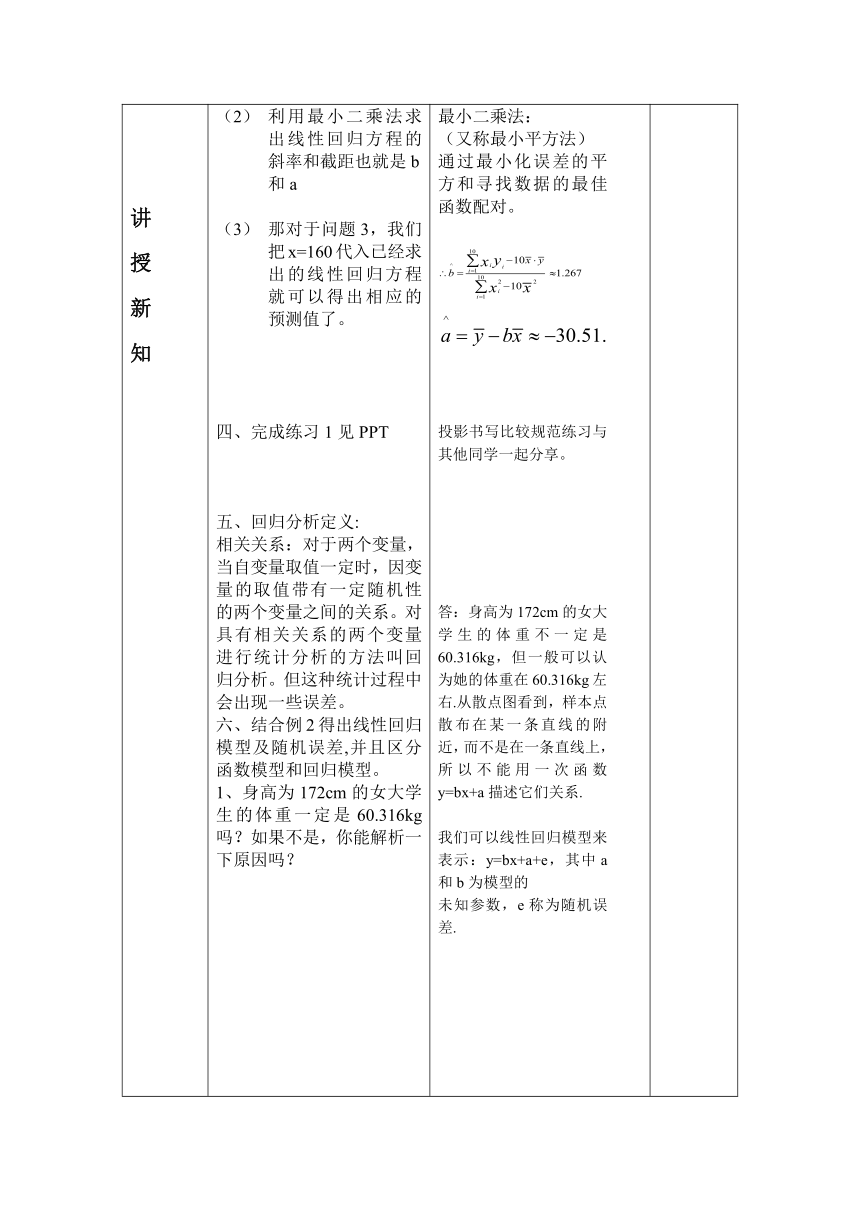
利用最小二乘法求出线性回归方程的斜率和截距也就是b和a
那对于问题3,我们把x=160代入已经求出的线性回归方程就可以得出相应的预测值了。
四、完成练习1见PPT
回归分析定义:
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。对具有相关关系的两个变量进行统计分析的方法叫回归分析。但这种统计过程中会出现一些误差。
结合例2得出线性回归模型及随机误差,并且区分函数模型和回归模型。
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
随机误差e的来源(可以推广到一般):
、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
、用线性回归模型近似真实模型所引起的误差;
、身高 y 的观测误差.
(1)答:要求解和
所以
最小二乘法:
(又称最小平方法)
通过最小化误差的平方和寻找数据的最佳函数配对。
投影书写比较规范练习与其他同学一起分享。
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重在60.316kg左右.从散点图看到,样本点散布在某一条直线的附近,而不是在一条直线上,所以不能用一次函数y=bx+a描述它们关系.
我们可以线性回归模型来表示:y=bx+a+e,其中a和b为模型的
未知参数,e称为随机误差.
以上三项误差越小,说明我们的回归方程的拟合效果越好,用
回归方程来预测就越准确。
讲 授
新
知 引入相关指数R2公式
八、讲解例题3:先求出y对x的回归直线方程,再说明拟合效果的好坏 显然,当R2的值越大,说明残差所占的比例越小,回归效果约好;反之,回归效果越差.一般的,当R2越接近于1,说明解释变量和预报变量之间的相关性越强,如果同一个问题,采用不同的回归方法分析,我们可以通过选择R2大的来作为回归模型.
结论:一般方法:
1.利用散点图观察两个变量是否线性相关
2.利用相关系数r来说明两个变量线性相关的强弱
3.利用相关指数来判断模型拟合的效果好不好。(残差分析)
考到拟合效果很少用这个公式,有时候直接用绝对值来比较.
九、建立回归模型的基本步骤:
1) 确定解释变量和预报变量;
2) 画出散点图;
3) 确定回归方程类型;
4) 求出回归方程;
5) 利用相关指数进行残差分析,检验拟合效果.
说明拟合效果较好。
其中在确定回归方程类型的时候不一定用直线,如果回归方程是直线就用必修3学过的最小二乘法求出回归直线方程的斜率和截距。如果不是直线方程要学会转化。(下节课讲解)
小
结
求回归直线方程的步骤:
写出直线方程为y=bx+a,即为所求的回归直线方程。
应用:利用回归直线方程对总体进行线性相关性的检验
板书
设计
作业 科作业纸:书P96-习题11-1
练习册:P66-67-1.2.3.4.5
P69-2.4.5.6.7
湘教版选修2-3 第8.5节
【教学目标】
知识与技能
了解样本、样本容量、线性回归的概念,理解变量之间的相关系数的概念、相关系数、一元线性回归直线等概念。
过程与方法
熟练利用公式求相关系数,掌握求一元线性回归直线方程 的方法,加深理解线性回归模型的意义。判断变量间是否线性相关。
情感、态度与价值观
培养学生分析问题、解决问题的能力,收集数据和处理数据的能力。
【教材分析】
教学重点:让学生了解线性回归的基本思想和方法。
教学难点:掌握建立回归模型的基本步骤。
变量间的关系:
函数关系:自变量x确定y唯一确定;(确定关系)
相关关系:当自变量一定时,因变量的取值带有一定的随机性的两个变量之间的关系称为相关关系 。
例如:在水稻产量与施肥量的关系中,施肥量是可控制变量,而水稻产量是随机变量。因此只能说明水稻产量与施肥量是相关关系。
现实生活中相关关系大量存在,从某种意义上看,函数是一种理想的关系模型,而相关关系式一种更为一般的情况,因此更有研究相关关系的必要了。
一元线性回归分析
在具有相关关系的变量中如果因变量仅与一个变量有关,相应的统计分析成为一元回归分析;若与因变量与多个自变量有关,称为多元线性回归分析。
线性相关性检验:(相关系数检验法)
当 >0时,我们称其正相关;
当 <0时,我们称其负相关;
当 =0时,我们称其不相关。
教学过程 教师活动 学生活动 设计意图
引
入
新
知
问题一:如果有两个变量X和Y,那么这两个变量之间有什么关系呢?
(联系我们之前学过的知识,哪些涉及了两个变量并着重强调两个变量之间的关系呢?)
用身高和体重这个例子引出相关关系那么什么叫做相关关系呢?函数关系与相关关系之间又有什么异同点呢?
那么这节课我们就一起来研究一下相关关系。
答:
函数:涉及了两个变量,自变量X因变量Y,
随着自变量X的变化相应的有唯一的因变量Y与之对应
函数关系
相关关系
通过对两个变量之间关系的探讨,既复习了已学的函数知识,又引出这节课所要关注的相关关系。
讲
授
新
知
在此之前,我们先一起来看一道例题。
一、首先我们先一起分析一下表中所给数据,你能得到怎样的结论呢?
这是我们从表中数据直接得到的,一般情况下对于数据的处理我们除了可以采用列表法,还可以采用图像法。那么为了更加直观的反映整体走势,下面请同学们根据表中数据在坐标系中绘出相应各点。看看能得到什么样的结论呢?
(用excel绘制散点图)
我们发现绘制出的图形呈现一个一个的散点,我们称这样的图形为散点图。
并且从数据散点图看到有随着的增加而沿某
直线增加的趋势。并且这些散点是相对较均匀的分布在这条直线的两侧。那么这条直线就被我们叫做一元线性回归直线,
答:随着施化肥量的增加,产量Y也是在逐年增加的;并且产量Y整体呈现一种上升的趋势。
通过学生对数据的观察可以大概得到两个变量间的关系,但是未来更加直观便可以借助散点图来帮助我们分析。
讲
授
新
知
那么这条直线该如何确定呢?(为了解决确定直线的问题,我们先给出一些必要的公式。)
二、下面介绍一个新的名词定义——相关系数。
当 时,…………
我们称其为相关系数、并且相关系数有如下几条性质:
1、正相关、负相关和不相关;(主要根据90至91页的图形加以说明)
2、.相关系数的取值为[-1,1]
3、相关系数的大小与相关程度的关系。
从90页的六个散点图中,我们可以发现散点图的密集程度是不一样的,并且这种密集程度与相关系数有着一定的联系,相关系数越接近1,X,Y的线性相关性越强,并随着X的增加Y也在线性增加。
讲
授
新
知
讲
授
新
知 三、既然学习了相关系数,下面我们就一起来解决例1中的3个问题。
首先我们先一起来计算一下例一中两个变量X、Y的相关系数。
要计算相关系数,就要求解哪些量呢?
(我们发现很接近1,说明钢水的含碳量x与冶炼时间y 正相关,即随着X的增加Y也是在增加的。就此我们可以预测出钢水的含碳量x增加时,冶炼时间y也会增加。)
利用最小二乘法求出线性回归方程的斜率和截距也就是b和a
那对于问题3,我们把x=160代入已经求出的线性回归方程就可以得出相应的预测值了。
四、完成练习1见PPT
回归分析定义:
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。对具有相关关系的两个变量进行统计分析的方法叫回归分析。但这种统计过程中会出现一些误差。
结合例2得出线性回归模型及随机误差,并且区分函数模型和回归模型。
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
随机误差e的来源(可以推广到一般):
、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
、用线性回归模型近似真实模型所引起的误差;
、身高 y 的观测误差.
(1)答:要求解和
所以
最小二乘法:
(又称最小平方法)
通过最小化误差的平方和寻找数据的最佳函数配对。
投影书写比较规范练习与其他同学一起分享。
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重在60.316kg左右.从散点图看到,样本点散布在某一条直线的附近,而不是在一条直线上,所以不能用一次函数y=bx+a描述它们关系.
我们可以线性回归模型来表示:y=bx+a+e,其中a和b为模型的
未知参数,e称为随机误差.
以上三项误差越小,说明我们的回归方程的拟合效果越好,用
回归方程来预测就越准确。
讲 授
新
知 引入相关指数R2公式
八、讲解例题3:先求出y对x的回归直线方程,再说明拟合效果的好坏 显然,当R2的值越大,说明残差所占的比例越小,回归效果约好;反之,回归效果越差.一般的,当R2越接近于1,说明解释变量和预报变量之间的相关性越强,如果同一个问题,采用不同的回归方法分析,我们可以通过选择R2大的来作为回归模型.
结论:一般方法:
1.利用散点图观察两个变量是否线性相关
2.利用相关系数r来说明两个变量线性相关的强弱
3.利用相关指数来判断模型拟合的效果好不好。(残差分析)
考到拟合效果很少用这个公式,有时候直接用绝对值来比较.
九、建立回归模型的基本步骤:
1) 确定解释变量和预报变量;
2) 画出散点图;
3) 确定回归方程类型;
4) 求出回归方程;
5) 利用相关指数进行残差分析,检验拟合效果.
说明拟合效果较好。
其中在确定回归方程类型的时候不一定用直线,如果回归方程是直线就用必修3学过的最小二乘法求出回归直线方程的斜率和截距。如果不是直线方程要学会转化。(下节课讲解)
小
结
求回归直线方程的步骤:
写出直线方程为y=bx+a,即为所求的回归直线方程。
应用:利用回归直线方程对总体进行线性相关性的检验
板书
设计
作业 科作业纸:书P96-习题11-1
练习册:P66-67-1.2.3.4.5
P69-2.4.5.6.7
同课章节目录
