7.3.2组合数的性质和应用课件-湘教版数学选修2-3(15张PPT)
文档属性
| 名称 | 7.3.2组合数的性质和应用课件-湘教版数学选修2-3(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:31:50 | ||
图片预览






文档简介
组合数的性质和应用
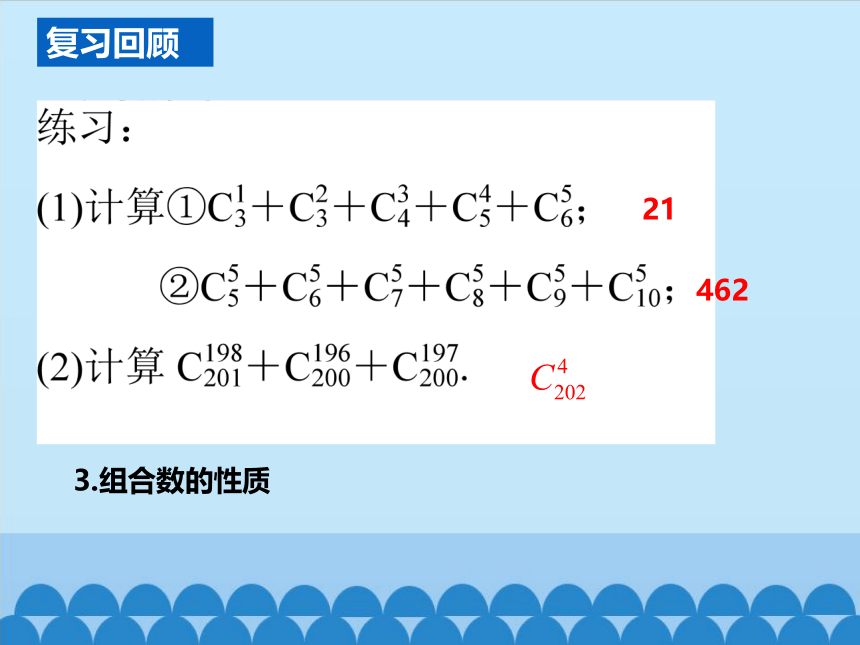
复习回顾
1.组合的概念
2.组合数的公式
3.组合数的性质
21
462
例1
直接法
间接法
题型一 有限制条件的组合问题
例2
变式:抽取的3件中至多1件是次品,抽法有多少种?(只需列出式子,不用计算结果)
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
题型二 与几何问题有关的组合问题
例3 (1)四面体的一个顶点为A,从其他顶点和各棱中点中取3个点,使它们和点A在同一平面上,有多少种不同的取法?
例3 (2)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,有多少种不同的取法.
方法点拨 利用组合知识解决与几何有关的问题时要注意:
(1)将已知条件中的元素的特征搞清,是用直接法还是用间接法;
(2)要使用分类方法,至于怎样确定分类标准,要具体问题具体分析;
(3)常用间接法解决该类问题.
思考1.在如图所示的四棱锥中,顶点为P,从其他的顶点和各棱的中点中取3个,使它们和点P在同一个平面内,不同的取法种数为___________.
谢谢!
复习回顾
1.组合的概念
2.组合数的公式
3.组合数的性质
21
462
例1
直接法
间接法
题型一 有限制条件的组合问题
例2
变式:抽取的3件中至多1件是次品,抽法有多少种?(只需列出式子,不用计算结果)
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
例2 有编号为1,2,3,4的4个盒子和4个不球,把小球全部放入盒内,问:
(1)共有多少种做法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒子不放球,有多少种放法?
题型二 与几何问题有关的组合问题
例3 (1)四面体的一个顶点为A,从其他顶点和各棱中点中取3个点,使它们和点A在同一平面上,有多少种不同的取法?
例3 (2)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,有多少种不同的取法.
方法点拨 利用组合知识解决与几何有关的问题时要注意:
(1)将已知条件中的元素的特征搞清,是用直接法还是用间接法;
(2)要使用分类方法,至于怎样确定分类标准,要具体问题具体分析;
(3)常用间接法解决该类问题.
思考1.在如图所示的四棱锥中,顶点为P,从其他的顶点和各棱的中点中取3个,使它们和点P在同一个平面内,不同的取法种数为___________.
谢谢!
同课章节目录
