7.1.2两个计数原理课件-湘教版数学选修2-3(25张PPT)
文档属性
| 名称 | 7.1.2两个计数原理课件-湘教版数学选修2-3(25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:37:40 | ||
图片预览





文档简介
7.1两个计数原理
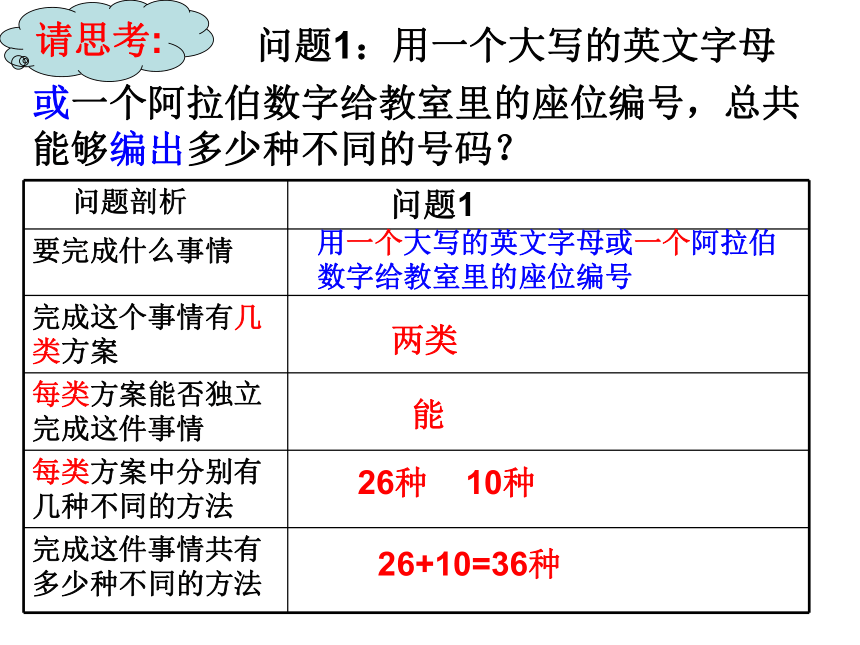
问题剖析
问题1
要完成什么事情
完成这个事情有几类方案
每类方案能否独立完成这件事情
每类方案中分别有几种不同的方法
完成这件事情共有多少种不同的方法
两类
能
26种 10种
26+10=36种
或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
请思考:
问题1:用一个大写的英文字母
用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号
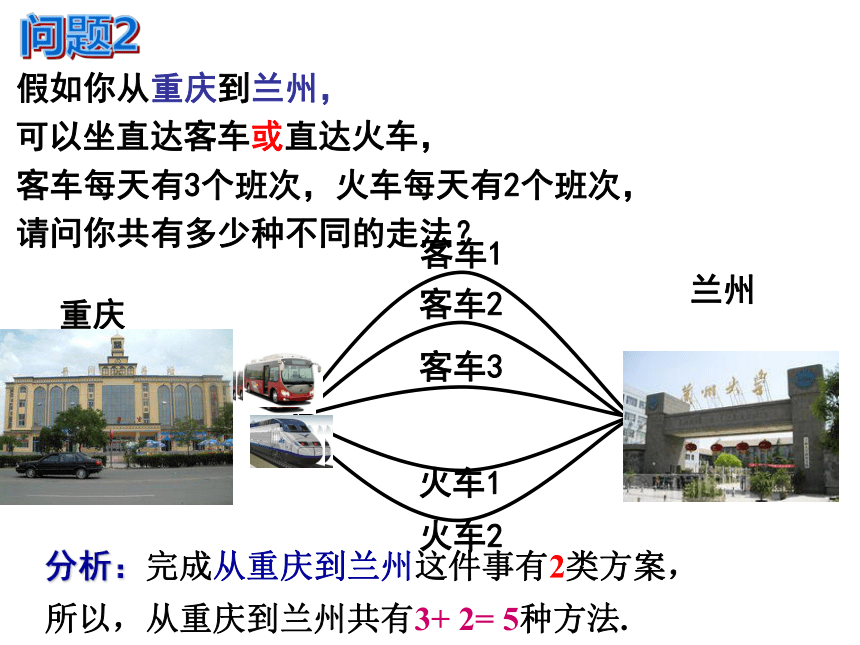
假如你从重庆到兰州,
请问你共有多少种不同的走法?
客车每天有3个班次,火车每天有2个班次,
可以坐直达客车或直达火车,
客车1
客车2
客车3
火车1
火车2
重庆
兰州
分析:完成从重庆到兰州这件事有2类方案,
所以,从重庆到兰州共有3+ 2= 5种方法.
完成一件事有两类不同的方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有
N = m + n
种不同的方法。
如果完成一件事情有n类不同方案,在每一类中都有若干种不同方法,那么应当如何计数呢?
完成一件事有 n 类不同的方案,
在第1类方案中有 m1 种不同的方法,
在第2类方案中有 m2 种不同的方法,
那么完成这件事共有
种不同的方法。
… …
在第n类方案中有mn种不同的方法,
例1.在填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
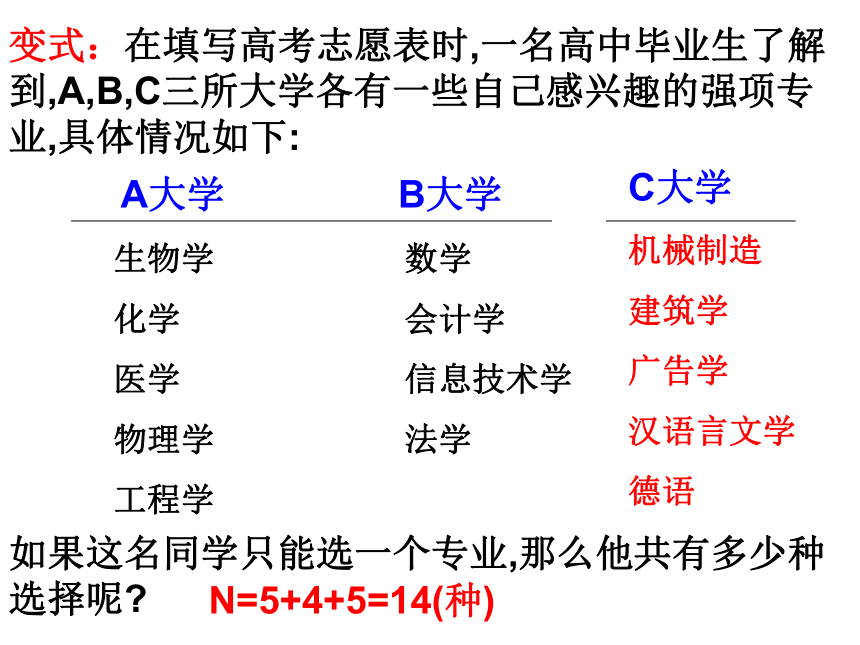
变式:在填写高考志愿表时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
C大学
机械制造
建筑学
广告学
汉语言文学
德语
N=5+4+5=14(种)
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
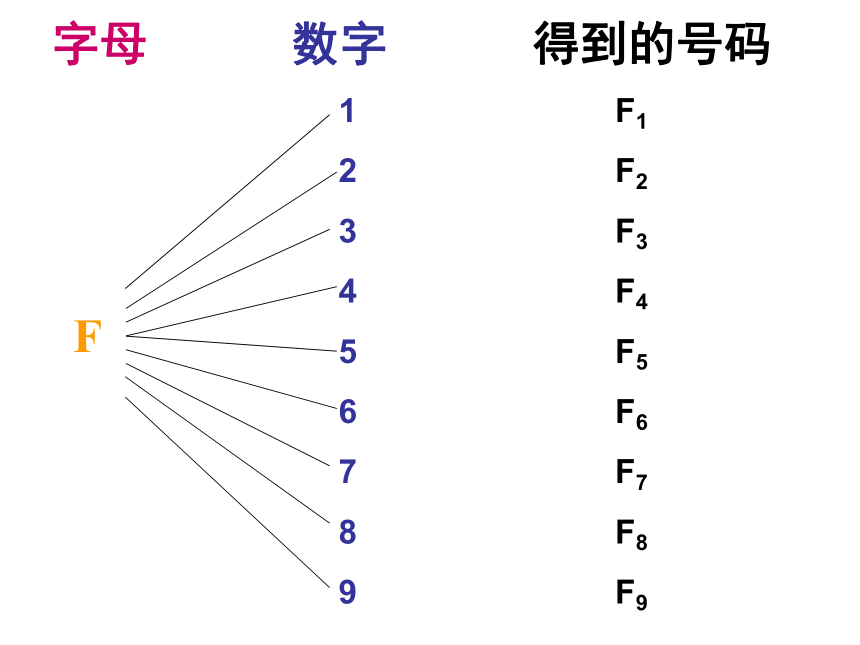
变式:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
字母 数字 得到的号码
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
A
B
B1
B2
B3
B4
B5
B6
B7
B8
B9
C
C1
C2
C3
C4
C5
C6
C7
C8
C9
D
D1
D2
D3
D4
D5
D6
D7
D8
D9
E
E1
E2
E3
E4
E5
E6
E7
E8
E9
F
F1
F2
F3
F4
F5
F6
F7
F8
F9
变式:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
分析:完成给教室里的座位编号这件事需要
两个步骤,
第1步,确定一个英文字母,有6种不同方法;
第2步,确定一个阿拉伯数字,有9种不同方法;
所以,编号共有6×9=54种方法.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有
种不同的方法.
N=m+n
分类加法计数原理:
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法.那么完成这件事共有
N=m×n
分步乘法计数原理:
种不同的方法.
例2: 在兰州读书的你欲回老家重庆过年,受雪灾影响兰州到重庆的火车全部停运.于是你决定先乘火车到宝鸡,然后第二天再乘汽车到重庆.一天中,火车有3班,汽车有2班,问你一共有多少种走法?
第二步, 由宝鸡去重庆有2种方法;
分析:
第一步, 由兰州去宝鸡有3种方法,
所以 从兰州经宝鸡到重庆共有3 ×2 = 6 种不同的方法。
汽车1
汽车2
宝鸡
兰州
重庆
火车1
火车 3
火车2
[ 变式]:如果你回家的时候需要转车后再乘飞机(如图),则共有多少种不同的走法?
汽车2
汽车1
火车 3
火车2
火车1
飞机1
飞机2
兰州
重庆
A地
B地
共有 :3×2×2=12种
那么完成这件事共有
种不同的方法。
完成一件事需要n个步骤,
做第1步有m1 种不同的方法,
做第2步有m2种不同的方法,
… …
做第n步有mn种不同的方法,
区别
分类计数原理(加法原理)
一般地,若完成一件事,有 n 类办法,在第1类办法中有 m1 种不同的方法,在第2类办法中有 m2 种不同的方法,…,在第 n 类办法中有 mn 种不同的方法,那么完成这件事共有:
种不同的方法.
分步计数原理 (乘法原理)
一般地,若完成一件事,需要分成 n 步,做第1步有 m1 种不同的方法,做第2步有 m2 种不同的方法,…,做第 n 步有 mn 种不同的方法,那么完成这件事共有:
种不同的方法.
做一件事情可以分为几类办法,每一类都可以独立完成这件事情
做一件事情要分为几步,每一步都完成了才能完成这件事情
解答计数问题的一般思维过程:
完成一件什么事
如何完成这件事
利用加法原理进行计数
方法的分类
过程的分步
利用乘法原理进行计数
解:从书架上任取1本书,
练习1 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
第1类方法是从第1层取1本计算机书,有4种方法;
第2类方法是从第2层取1本文艺书,有3种方法;
第3类方法是从第3层取1本体育书,有2种方法。
根据分类加法计数原理,不同取法的种数是:N=4+3+2=9.
(1)从书架上任取1本书,有几种不同的取法?
有三类方法:
(2)从书架上的第1、2、3层各取1本书,有几种不同的取法?
练习1 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
(1)从书架上任取1本书,有几种不同的取法?
解:从书架的第1,2,3层各取1本书,
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法。
根据分步计数原理,不同取法的种数是:N=4×3×2=24.
可以分成三个步骤完成:
练习2 要从甲、乙、丙、3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
甲
乙
丙
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从3幅画中选1幅挂在左边墙上,有3种选法;
第二步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法。
根据分步计数原理,不同挂法的种数是:N=3×2=6.
变式 要从甲、乙、丙、丁、戊5幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
甲
乙
丙
丁
戊
解:从5幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从5幅画中选1幅挂在左边墙上,有5种选法;
第二步,从剩下的4幅画中选1幅挂在右边墙上,有4种选法。
根据分步计数原理,不同挂法的种数是:N=5×4=20.
练习3:体育福利彩票的中奖号码有7位数码,每位数若是0~9这十个数字中任一个,则每次摇奖产生的号码有多少种可能?
10
=107
10
10
10
10
10
10
×
×
×
×
×
×
第一位
第二位
第三位
第四位
第五位
第六位
第七位
变1:这十个数字一共可以组成多少个7位数?
9
×
×
×
×
×
×
10
10
10
10
10
10
百万
十万
万
千
百
十
个
= 9×106
练习3:体育福利彩票的中奖号码有7位数码,每位数若是0~9这十个数字中任一个,则产生中奖号码所有可能的种数是多少?
变2: 0~9这十个数字可组成多少数字不重复的七位数?
×
×
×
×
×
×
9
9
8
7
=544320
6
5
4
百万
十万
万
千
百
十
个
1.本节课学习了哪些主要内容?
2.你如何来判别使用哪个计数原理?
共同点:
分类加法计数原理
分步乘法计数原理
①完成一件事有n类不同的方案;
②各类方案相互独立;
③每一类方案都能直接完成该事件。
完成一件事要n个不同的步骤;
每一个步骤都不能直接完成该事件,只有完成每个步骤,才能完成这件事。
各个步骤相互联系 ;
相互联系分步到达
相互独立
直达目的
都是有关“完成一件事情”的所有不同方法的种数问题。
主要不同点:
再 见
问题剖析
问题1
要完成什么事情
完成这个事情有几类方案
每类方案能否独立完成这件事情
每类方案中分别有几种不同的方法
完成这件事情共有多少种不同的方法
两类
能
26种 10种
26+10=36种
或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
请思考:
问题1:用一个大写的英文字母
用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号
假如你从重庆到兰州,
请问你共有多少种不同的走法?
客车每天有3个班次,火车每天有2个班次,
可以坐直达客车或直达火车,
客车1
客车2
客车3
火车1
火车2
重庆
兰州
分析:完成从重庆到兰州这件事有2类方案,
所以,从重庆到兰州共有3+ 2= 5种方法.
完成一件事有两类不同的方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有
N = m + n
种不同的方法。
如果完成一件事情有n类不同方案,在每一类中都有若干种不同方法,那么应当如何计数呢?
完成一件事有 n 类不同的方案,
在第1类方案中有 m1 种不同的方法,
在第2类方案中有 m2 种不同的方法,
那么完成这件事共有
种不同的方法。
… …
在第n类方案中有mn种不同的方法,
例1.在填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
变式:在填写高考志愿表时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
C大学
机械制造
建筑学
广告学
汉语言文学
德语
N=5+4+5=14(种)
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
变式:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
字母 数字 得到的号码
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
A
B
B1
B2
B3
B4
B5
B6
B7
B8
B9
C
C1
C2
C3
C4
C5
C6
C7
C8
C9
D
D1
D2
D3
D4
D5
D6
D7
D8
D9
E
E1
E2
E3
E4
E5
E6
E7
E8
E9
F
F1
F2
F3
F4
F5
F6
F7
F8
F9
变式:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
分析:完成给教室里的座位编号这件事需要
两个步骤,
第1步,确定一个英文字母,有6种不同方法;
第2步,确定一个阿拉伯数字,有9种不同方法;
所以,编号共有6×9=54种方法.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有
种不同的方法.
N=m+n
分类加法计数原理:
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法.那么完成这件事共有
N=m×n
分步乘法计数原理:
种不同的方法.
例2: 在兰州读书的你欲回老家重庆过年,受雪灾影响兰州到重庆的火车全部停运.于是你决定先乘火车到宝鸡,然后第二天再乘汽车到重庆.一天中,火车有3班,汽车有2班,问你一共有多少种走法?
第二步, 由宝鸡去重庆有2种方法;
分析:
第一步, 由兰州去宝鸡有3种方法,
所以 从兰州经宝鸡到重庆共有3 ×2 = 6 种不同的方法。
汽车1
汽车2
宝鸡
兰州
重庆
火车1
火车 3
火车2
[ 变式]:如果你回家的时候需要转车后再乘飞机(如图),则共有多少种不同的走法?
汽车2
汽车1
火车 3
火车2
火车1
飞机1
飞机2
兰州
重庆
A地
B地
共有 :3×2×2=12种
那么完成这件事共有
种不同的方法。
完成一件事需要n个步骤,
做第1步有m1 种不同的方法,
做第2步有m2种不同的方法,
… …
做第n步有mn种不同的方法,
区别
分类计数原理(加法原理)
一般地,若完成一件事,有 n 类办法,在第1类办法中有 m1 种不同的方法,在第2类办法中有 m2 种不同的方法,…,在第 n 类办法中有 mn 种不同的方法,那么完成这件事共有:
种不同的方法.
分步计数原理 (乘法原理)
一般地,若完成一件事,需要分成 n 步,做第1步有 m1 种不同的方法,做第2步有 m2 种不同的方法,…,做第 n 步有 mn 种不同的方法,那么完成这件事共有:
种不同的方法.
做一件事情可以分为几类办法,每一类都可以独立完成这件事情
做一件事情要分为几步,每一步都完成了才能完成这件事情
解答计数问题的一般思维过程:
完成一件什么事
如何完成这件事
利用加法原理进行计数
方法的分类
过程的分步
利用乘法原理进行计数
解:从书架上任取1本书,
练习1 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
第1类方法是从第1层取1本计算机书,有4种方法;
第2类方法是从第2层取1本文艺书,有3种方法;
第3类方法是从第3层取1本体育书,有2种方法。
根据分类加法计数原理,不同取法的种数是:N=4+3+2=9.
(1)从书架上任取1本书,有几种不同的取法?
有三类方法:
(2)从书架上的第1、2、3层各取1本书,有几种不同的取法?
练习1 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
(1)从书架上任取1本书,有几种不同的取法?
解:从书架的第1,2,3层各取1本书,
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法。
根据分步计数原理,不同取法的种数是:N=4×3×2=24.
可以分成三个步骤完成:
练习2 要从甲、乙、丙、3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
甲
乙
丙
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从3幅画中选1幅挂在左边墙上,有3种选法;
第二步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法。
根据分步计数原理,不同挂法的种数是:N=3×2=6.
变式 要从甲、乙、丙、丁、戊5幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?
甲
乙
丙
丁
戊
解:从5幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从5幅画中选1幅挂在左边墙上,有5种选法;
第二步,从剩下的4幅画中选1幅挂在右边墙上,有4种选法。
根据分步计数原理,不同挂法的种数是:N=5×4=20.
练习3:体育福利彩票的中奖号码有7位数码,每位数若是0~9这十个数字中任一个,则每次摇奖产生的号码有多少种可能?
10
=107
10
10
10
10
10
10
×
×
×
×
×
×
第一位
第二位
第三位
第四位
第五位
第六位
第七位
变1:这十个数字一共可以组成多少个7位数?
9
×
×
×
×
×
×
10
10
10
10
10
10
百万
十万
万
千
百
十
个
= 9×106
练习3:体育福利彩票的中奖号码有7位数码,每位数若是0~9这十个数字中任一个,则产生中奖号码所有可能的种数是多少?
变2: 0~9这十个数字可组成多少数字不重复的七位数?
×
×
×
×
×
×
9
9
8
7
=544320
6
5
4
百万
十万
万
千
百
十
个
1.本节课学习了哪些主要内容?
2.你如何来判别使用哪个计数原理?
共同点:
分类加法计数原理
分步乘法计数原理
①完成一件事有n类不同的方案;
②各类方案相互独立;
③每一类方案都能直接完成该事件。
完成一件事要n个不同的步骤;
每一个步骤都不能直接完成该事件,只有完成每个步骤,才能完成这件事。
各个步骤相互联系 ;
相互联系分步到达
相互独立
直达目的
都是有关“完成一件事情”的所有不同方法的种数问题。
主要不同点:
再 见
同课章节目录
