7.4二项式定理课件-湘教版数学选修2-3(46张PPT)
文档属性
| 名称 | 7.4二项式定理课件-湘教版数学选修2-3(46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:38:41 | ||
图片预览











文档简介
二项式定理
问题
引航
1.二项式定理是什么?通项公式又是什么?
2.二项式定理有何结构特征,二项展开式中某项的二项式系数与某项的系数有区别吗?
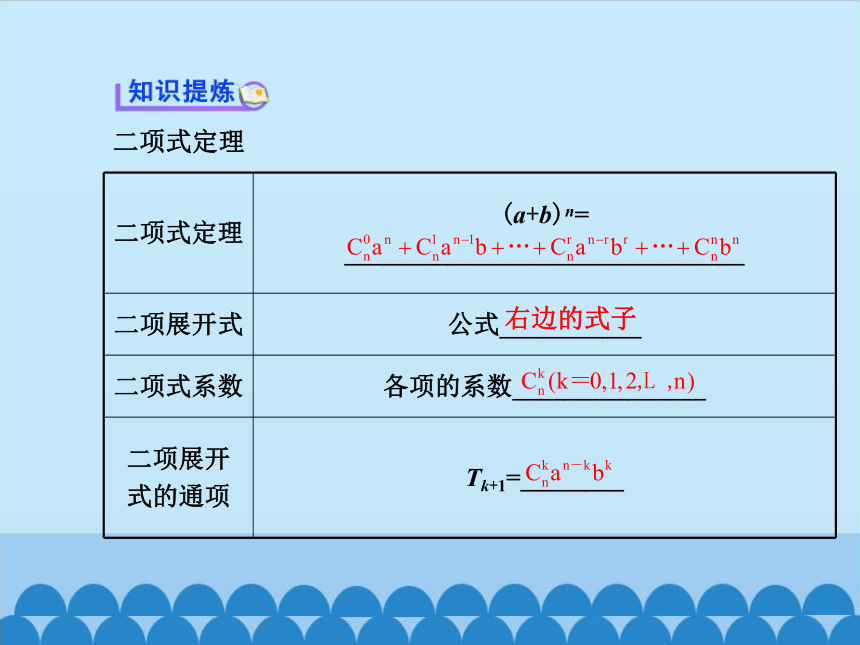
二项式定理
二项式定理
(a+b)n=
_______________________________
二项展开式
公式___________
二项式系数
各项的系数_______________
二项展开
式的通项
Tk+1=________
右边的式子
1.判一判 (正确的打“√”,错误的打“×”)
(1)(a+b)n展开式中共有n项.( )
(2)二项式(a+b)n与(b+a)n展开式中第r+1项相同.( )
(3) 是(a+b)n展开式中的第k项.( )
【解析】(1)错误.(a+b)n展开式中共有n+1项.
(2)错误.(a+b)n展开式中第r+1项为 ,而(b+a)n展开式
中第r+1项为
(3)错误. 是(a+b)n展开式中的第k+1项.
答案:(1)× (2)× (3)×
2.做一做(请把正确的答案写在横线上)
(1) 的二项展开式中第4项是________.
(2)展开 为__________.
(3)(1+x)7的展开式中x2项的系数是_________.
【解析】(1)展开式的通项公式为
所以第4项为
答案:
答案:
(3)(1+x)7展开式中
令k=2,得x2项的系数是 =21.
答案:21
【要点探究】
知识点 二项式定理及其通项公式
1.二项展开式的特点
(1)展开式共有n+1项.
(2)各项的次数和都等于二项式的幂指数n.
(3)字母a的幂指数按降幂排列,从第一项开始,次数由n逐项减1直到为0,字母b的幂指数按升幂排列,从第一项开始,次数由0逐项加1直到为n.
2.对通项公式的四点说明
(1)通项 是(a+b)n的展开式的第r+1项,这里r=0,1,
…,n.
(2)二项式(a+b)n的第r+1项 和(b+a)n的展开式的第r+1
项 是有区别的,应用二项式定理时,其中的a和b是不
能随便交换的.
(3)注意二项式系数 与展开式中对应项的系数不一定相等,
二项式系数一定为正,而项的系数有时可为负.
(4)通项公式是在(a+b)n这个标准形式下而言的,如(a-b)n的
二项展开式的通项公式是 (只需把-b看成b代
入二项式定理),这与 是不同的,在这里对应项的
二项式系数是相等的,都是 ,但项的系数一个是 ,一
个是 ,可看出二项式系数与项的系数是不同的概念.
【知识拓展】二项式定理的证明
(a+b)n是n个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或b.而且每个(a+b)中的a或b选定后才能得到展开式的一项.由分步计数原理可知展开式共有2n项(包括同类项),其中每一项都是an-kbk的形式,k=0,1,…,n;
对于每一项an-kbk,它是由n-k个(a+b)选了a,k个(a+b)选了b得到的,它出现的次数相当于从n个(a+b)中取k个b的组合数,将它们合并同类项,就得二项展开式,这就是二项式定理.
【微思考】
(1)(a+b)n展开式中各项前的系数代表着什么?
提示:各项前的系数依次为组合数 代表着这
些项在展开式中出现的次数.
(2)二项展开式中一定含有常数项吗?
提示:不一定.由 可知,也可能无常数项.
【即时练】
1.在 的二项展开式中,x5的系数为_____________.
【解析】因为
由题意知15-5r=5,解得r=2.
所以 即为所求x5的系数.
答案:40
2.(1+2x)5的展开式的第3项的系数为__________,第三项的二
项式系数为__________.
【解析】(1+2x)5的展开式的第3项的系数为 =40,第三项的
二项式系数为 =10.
答案:40 10
【题型示范】
类型一 二项式定理的正用和逆用
【典例1】
(1)计算:
(2)用二项式定理展开
【解题探究】1.题(1)中式子有什么结构特征?如何与二项式
定理联系?
2.题(2)中运用二项式定理展开二项式的关键是什么?
【探究提示】1.式子是按x-1的降幂排列的,但与二项式定理
比较可知式子中缺少(x-1)0项,进而可构造[(x-1)+1]5.
2.关键是记准展开式,根据二项式的结构特征进行必要的变形,
可使展开二项式的过程得到简化.
【自主解答】(1)原式=
答案:x5-1
(2)方法一:
方法二:
【方法技巧】运用二项式定理的解题策略
(1)正用:求形式简单的二项展开式时可直接由二项式定理展开,展开时注意二项展开式的特点:前一个字母是降幂,后一个字母是升幂.形如(a-b)n的展开式中会出现正负间隔的情况.对较繁杂的式子,先化简再用二项式定理展开.
(2)逆用:逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.
【变式训练】求二项式(a-2b)4的展开式.
【解析】根据二项式定理得
【误区警示】运用二项式定理时要注意对号入座,本题易误把-2b中的负号忽略.
【补偿训练】计算:
【解析】设
则
所以
答案:
类型二 求二项展开式的特定项
【典例2】
(1)(2014·湖南高考) 的展开式中x2y3的系数是( )
A.-20 B.-5 C.5 D.20
(2)二项式 的展开式中的常数项为______________.
【解题探究】
1.题(1)中x2y3是二项式 的展开式中的第几项?
2.题(2)中二项展开式中的常数项有什么特征?
【探究提示】1.由通项公式可知,x2y3是二项式 展开式中的第4项.
2.对于常数项,隐含条件是字母的指数为0(即0次项).
【自主解答】(1)选A.因为 所以x2y3的
系数是-20.
令6-2r=0,得r=3,
所以
答案:-20
【延伸探究】题(2)中第3项的系数为________,第3项的二项
式系数为________.
【解析】因为
所以二项展开式中第3项的系数为60,第3项的二项式系数为
答案:60 15
【方法技巧】1.求二项展开式特定项的步骤
2.求二项展开式的特定项常见题型及处理措施
(1)求第k项.
(2)求常数项.对于常数项,隐含条件是字母的指数为0(即0次项).
(3)求有理项.对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.
(4)求整式项.求二项展开式中的整式项,其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.
提醒:在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
3.正确区分二项式系数与指定某一项的系数
二项式系数与项的系数是两个不同的概念,前者仅与二项式的指数及项数有关,与二项式无关,后者与二项式、二项式的指数及项数均有关.
【变式训练】求二项式 展开式中的有理项.
【解题指南】写出展开式的通项,令通项公式中x的指数是整
数.
【解析】
令 ∈Z(0≤r≤9),得r=3或r=9,
所以当r=3时,
当r=9时,
综上:展开式中的有理项为-84x4与-x3.
【补偿训练】若 展开式的常数项为60,则常数a的值
为________.
【解析】由二项式定理可知
令6-3r=0,得r=2,所以
所以15a=60,所以a=4.
答案:4
【拓展类型】二项式定理的应用(整除问题)
【备选例题】(1)8011被9除的余数为______.
(2)证明:32n+2-8n-9(n∈N*)能被64整除.
【解析】(1)因为
=81k-1(k∈Z),
因为k∈Z,所以81k-1∈Z,所以81k-1被9除余8,即8011被9除的
余数为8.
答案:8
由于各项均能被64整除,所以32n+2-8n-9(n∈N*)能被64整除.
【方法技巧】整除性问题或求余数问题的处理方法
(1)解决这类问题,必须构造一个与题目条件有关的二项式.
(2)用二项式定理解决an+b整除(或余数)问题时,一般需要将底数写成除数m的整数倍加上或减去r(1≤r<m)的形式,利用二项展开式求解.
(3)要注意余数的范围,a=cr+b式子中b为余数,b∈[0,r),r是除数,利用二项式定理展开式变形后,若剩余部分是负数要注意转换.
(4)利用二项式定量证明有关多项式(数值)的整除问题时,关键是将所给多项式通过恒等变形变为二项式形式,使其展开后的各项均含有除式.
【易错误区】混淆二项式系数与项的系数而致误
【典例】(2014·日照高二检测)若(x- )n的展开式中第二项
与第四项的系数之比为1∶2,则展开式中第三项的二项式系数
为________.
【解析】(x- )n的展开式中第二项与第四项分别为
由题意得 ①,
即n2-3n-4=0,
解得n=4或n=-1(舍去).
所以 ②
所以第三项的二项式系数为 =6.
答案:6
【常见误区】
错解
错 因 剖 析
10
在①处错误地认为第二项的系数为 ,第四项的系数为
而得到错误的n值
12
在②处错误地认为二项式系数为项的系数
【防范措施】
1.注意概念的区分
对概念的把握和区分在解题中往往起到关键的作用.如本例易将“二项展开式中的二项式系数”与“二项展开式中项的系数”混为一谈.
2.审题细致看清条件
在解决二项式问题时,一定注意分析问题具体是哪一项,到底是什么样的系数.熟练把握二项式定理及通项公式.同时要养成良好的思维习惯.如本例条件是“第二项与第四项的系数”,一是指明第二项和第四项,二是指明是系数而不是二项式系数.
【类题试解】(1)(2014·临沂高二检测)若 的二项展
开式中x3的系数为 ,则a=____________(用数字作答).
【解析】因为 ,当12-3r=3时,r=3,
所以 ,即a=2.
答案:2
(2)已知 的展开式中第5项的二项式系数与第3项的二
项式系数的比为14∶3,则展开式中的常数项为________.
【解析】由已知条件得: =14∶3,整理得:n2-5n-50=0,
所以n=10,
所以展开式的通项为:
令 ,得k=2,
所以常数项为第三项
答案:180
谢谢
问题
引航
1.二项式定理是什么?通项公式又是什么?
2.二项式定理有何结构特征,二项展开式中某项的二项式系数与某项的系数有区别吗?
二项式定理
二项式定理
(a+b)n=
_______________________________
二项展开式
公式___________
二项式系数
各项的系数_______________
二项展开
式的通项
Tk+1=________
右边的式子
1.判一判 (正确的打“√”,错误的打“×”)
(1)(a+b)n展开式中共有n项.( )
(2)二项式(a+b)n与(b+a)n展开式中第r+1项相同.( )
(3) 是(a+b)n展开式中的第k项.( )
【解析】(1)错误.(a+b)n展开式中共有n+1项.
(2)错误.(a+b)n展开式中第r+1项为 ,而(b+a)n展开式
中第r+1项为
(3)错误. 是(a+b)n展开式中的第k+1项.
答案:(1)× (2)× (3)×
2.做一做(请把正确的答案写在横线上)
(1) 的二项展开式中第4项是________.
(2)展开 为__________.
(3)(1+x)7的展开式中x2项的系数是_________.
【解析】(1)展开式的通项公式为
所以第4项为
答案:
答案:
(3)(1+x)7展开式中
令k=2,得x2项的系数是 =21.
答案:21
【要点探究】
知识点 二项式定理及其通项公式
1.二项展开式的特点
(1)展开式共有n+1项.
(2)各项的次数和都等于二项式的幂指数n.
(3)字母a的幂指数按降幂排列,从第一项开始,次数由n逐项减1直到为0,字母b的幂指数按升幂排列,从第一项开始,次数由0逐项加1直到为n.
2.对通项公式的四点说明
(1)通项 是(a+b)n的展开式的第r+1项,这里r=0,1,
…,n.
(2)二项式(a+b)n的第r+1项 和(b+a)n的展开式的第r+1
项 是有区别的,应用二项式定理时,其中的a和b是不
能随便交换的.
(3)注意二项式系数 与展开式中对应项的系数不一定相等,
二项式系数一定为正,而项的系数有时可为负.
(4)通项公式是在(a+b)n这个标准形式下而言的,如(a-b)n的
二项展开式的通项公式是 (只需把-b看成b代
入二项式定理),这与 是不同的,在这里对应项的
二项式系数是相等的,都是 ,但项的系数一个是 ,一
个是 ,可看出二项式系数与项的系数是不同的概念.
【知识拓展】二项式定理的证明
(a+b)n是n个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或b.而且每个(a+b)中的a或b选定后才能得到展开式的一项.由分步计数原理可知展开式共有2n项(包括同类项),其中每一项都是an-kbk的形式,k=0,1,…,n;
对于每一项an-kbk,它是由n-k个(a+b)选了a,k个(a+b)选了b得到的,它出现的次数相当于从n个(a+b)中取k个b的组合数,将它们合并同类项,就得二项展开式,这就是二项式定理.
【微思考】
(1)(a+b)n展开式中各项前的系数代表着什么?
提示:各项前的系数依次为组合数 代表着这
些项在展开式中出现的次数.
(2)二项展开式中一定含有常数项吗?
提示:不一定.由 可知,也可能无常数项.
【即时练】
1.在 的二项展开式中,x5的系数为_____________.
【解析】因为
由题意知15-5r=5,解得r=2.
所以 即为所求x5的系数.
答案:40
2.(1+2x)5的展开式的第3项的系数为__________,第三项的二
项式系数为__________.
【解析】(1+2x)5的展开式的第3项的系数为 =40,第三项的
二项式系数为 =10.
答案:40 10
【题型示范】
类型一 二项式定理的正用和逆用
【典例1】
(1)计算:
(2)用二项式定理展开
【解题探究】1.题(1)中式子有什么结构特征?如何与二项式
定理联系?
2.题(2)中运用二项式定理展开二项式的关键是什么?
【探究提示】1.式子是按x-1的降幂排列的,但与二项式定理
比较可知式子中缺少(x-1)0项,进而可构造[(x-1)+1]5.
2.关键是记准展开式,根据二项式的结构特征进行必要的变形,
可使展开二项式的过程得到简化.
【自主解答】(1)原式=
答案:x5-1
(2)方法一:
方法二:
【方法技巧】运用二项式定理的解题策略
(1)正用:求形式简单的二项展开式时可直接由二项式定理展开,展开时注意二项展开式的特点:前一个字母是降幂,后一个字母是升幂.形如(a-b)n的展开式中会出现正负间隔的情况.对较繁杂的式子,先化简再用二项式定理展开.
(2)逆用:逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.
【变式训练】求二项式(a-2b)4的展开式.
【解析】根据二项式定理得
【误区警示】运用二项式定理时要注意对号入座,本题易误把-2b中的负号忽略.
【补偿训练】计算:
【解析】设
则
所以
答案:
类型二 求二项展开式的特定项
【典例2】
(1)(2014·湖南高考) 的展开式中x2y3的系数是( )
A.-20 B.-5 C.5 D.20
(2)二项式 的展开式中的常数项为______________.
【解题探究】
1.题(1)中x2y3是二项式 的展开式中的第几项?
2.题(2)中二项展开式中的常数项有什么特征?
【探究提示】1.由通项公式可知,x2y3是二项式 展开式中的第4项.
2.对于常数项,隐含条件是字母的指数为0(即0次项).
【自主解答】(1)选A.因为 所以x2y3的
系数是-20.
令6-2r=0,得r=3,
所以
答案:-20
【延伸探究】题(2)中第3项的系数为________,第3项的二项
式系数为________.
【解析】因为
所以二项展开式中第3项的系数为60,第3项的二项式系数为
答案:60 15
【方法技巧】1.求二项展开式特定项的步骤
2.求二项展开式的特定项常见题型及处理措施
(1)求第k项.
(2)求常数项.对于常数项,隐含条件是字母的指数为0(即0次项).
(3)求有理项.对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.
(4)求整式项.求二项展开式中的整式项,其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.
提醒:在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
3.正确区分二项式系数与指定某一项的系数
二项式系数与项的系数是两个不同的概念,前者仅与二项式的指数及项数有关,与二项式无关,后者与二项式、二项式的指数及项数均有关.
【变式训练】求二项式 展开式中的有理项.
【解题指南】写出展开式的通项,令通项公式中x的指数是整
数.
【解析】
令 ∈Z(0≤r≤9),得r=3或r=9,
所以当r=3时,
当r=9时,
综上:展开式中的有理项为-84x4与-x3.
【补偿训练】若 展开式的常数项为60,则常数a的值
为________.
【解析】由二项式定理可知
令6-3r=0,得r=2,所以
所以15a=60,所以a=4.
答案:4
【拓展类型】二项式定理的应用(整除问题)
【备选例题】(1)8011被9除的余数为______.
(2)证明:32n+2-8n-9(n∈N*)能被64整除.
【解析】(1)因为
=81k-1(k∈Z),
因为k∈Z,所以81k-1∈Z,所以81k-1被9除余8,即8011被9除的
余数为8.
答案:8
由于各项均能被64整除,所以32n+2-8n-9(n∈N*)能被64整除.
【方法技巧】整除性问题或求余数问题的处理方法
(1)解决这类问题,必须构造一个与题目条件有关的二项式.
(2)用二项式定理解决an+b整除(或余数)问题时,一般需要将底数写成除数m的整数倍加上或减去r(1≤r<m)的形式,利用二项展开式求解.
(3)要注意余数的范围,a=cr+b式子中b为余数,b∈[0,r),r是除数,利用二项式定理展开式变形后,若剩余部分是负数要注意转换.
(4)利用二项式定量证明有关多项式(数值)的整除问题时,关键是将所给多项式通过恒等变形变为二项式形式,使其展开后的各项均含有除式.
【易错误区】混淆二项式系数与项的系数而致误
【典例】(2014·日照高二检测)若(x- )n的展开式中第二项
与第四项的系数之比为1∶2,则展开式中第三项的二项式系数
为________.
【解析】(x- )n的展开式中第二项与第四项分别为
由题意得 ①,
即n2-3n-4=0,
解得n=4或n=-1(舍去).
所以 ②
所以第三项的二项式系数为 =6.
答案:6
【常见误区】
错解
错 因 剖 析
10
在①处错误地认为第二项的系数为 ,第四项的系数为
而得到错误的n值
12
在②处错误地认为二项式系数为项的系数
【防范措施】
1.注意概念的区分
对概念的把握和区分在解题中往往起到关键的作用.如本例易将“二项展开式中的二项式系数”与“二项展开式中项的系数”混为一谈.
2.审题细致看清条件
在解决二项式问题时,一定注意分析问题具体是哪一项,到底是什么样的系数.熟练把握二项式定理及通项公式.同时要养成良好的思维习惯.如本例条件是“第二项与第四项的系数”,一是指明第二项和第四项,二是指明是系数而不是二项式系数.
【类题试解】(1)(2014·临沂高二检测)若 的二项展
开式中x3的系数为 ,则a=____________(用数字作答).
【解析】因为 ,当12-3r=3时,r=3,
所以 ,即a=2.
答案:2
(2)已知 的展开式中第5项的二项式系数与第3项的二
项式系数的比为14∶3,则展开式中的常数项为________.
【解析】由已知条件得: =14∶3,整理得:n2-5n-50=0,
所以n=10,
所以展开式的通项为:
令 ,得k=2,
所以常数项为第三项
答案:180
谢谢
同课章节目录
