8.2.7随机变量的方差课件-湘教版数学选修2-3(28张PPT)
文档属性
| 名称 | 8.2.7随机变量的方差课件-湘教版数学选修2-3(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 583.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:42:54 | ||
图片预览








文档简介
随机变量的方差
问题
引航
1.离散型随机变量的方差及标准差的定义是什么?
2.方差具有哪些性质?两点分布与二项分布的方差分别是什么?
3.如何计算简单离散型随机变量的方差?
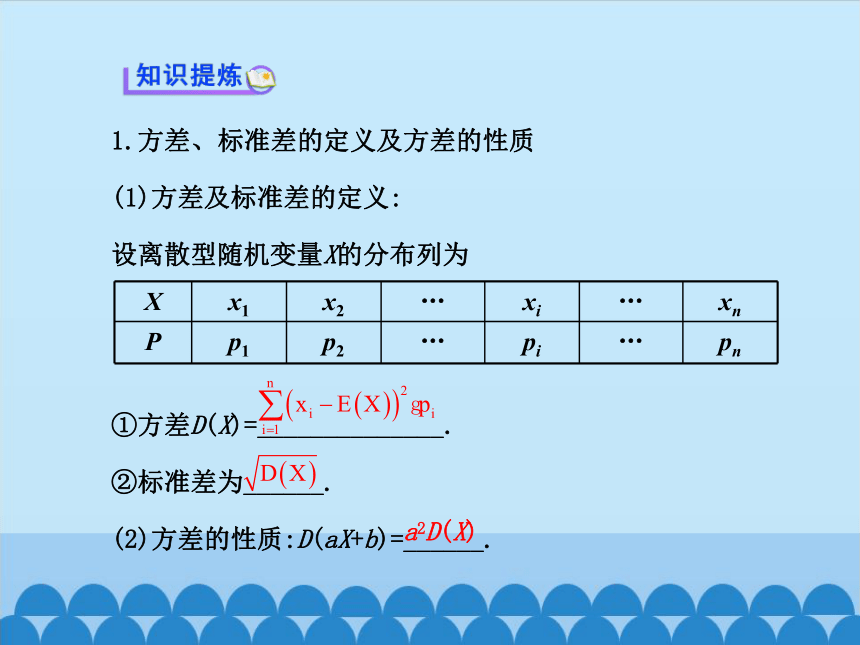
1.方差、标准差的定义及方差的性质
(1)方差及标准差的定义:
设离散型随机变量X的分布列为
①方差D(X)=______________.
②标准差为______.
(2)方差的性质:D(aX+b)=______.
X
x1
x2
…
xi
…
xn
P
p1
p2
…
pi
…
pn
a2D(X)
2.两个常见分布的方差
(1)若X服从两点分布,则D(X)=_______.
(2)若X~B(n,p),则D(X)=________.
p(1-p)
np(1-p)
1.判一判(正确的打“√”,错误的打“×”)
(1)离散型随机变量的方差越大,随机变量越稳定. ( )
(2)若a是常数,则D(a)=0. ( )
(3)离散型随机变量的方差反映了随机变量偏离于期望的平均程度. ( )
【解析】(1)错误.离散型随机变量的方差越大,随机变量越不稳定.
(2)正确.因为E(a)=a,所以D(a)=0.
(3)正确.由离散型随机变量的方差的几何意义可知,其反映了随机变量偏离于期望的平均程度.
答案:(1)× (2)√ (3)√
2.做一做(请把正确的答案写在横线上)
(1)若随机变量X服从两点分布,且成功的概率p=0.5,则E(X)和
D(X)分别为 .
(2)设随机变量ξ~B ,则D(ξ)= .
(3)如果X是离散型随机变量,Y=3X+2,那么D(Y)= D(X).
【解析】(1)因为X服从两点分布,
所以X的概率分布为
所以E(X)=0×0.5+1×0.5=0.5,
D(X)=0.52×0.5+(1-0.5)2×0.5=0.25.
答案:0.5和0.25
X
0
1
P
0.5
0.5
(2)因为随机变量ξ~B ,
所以D(ξ)=
答案:
(3)由于X是离散型随机变量,Y=3X+2呈线性关系,代入公式,则
E(Y)=3E(X)+2,D(Y)=32D(X)=9D(X).
答案:9
【要点探究】
知识点 方差、标准差的定义及方差的性质
1.对随机变量X的方差、标准差的五点说明
(1)随机变量X的方差的定义与一组数据的方差的定义是相同的.
(2)随机变量X的方差和标准差都反映了随机变量X取值的稳定性和波动、集中与离散程度.
(3)D(X)越小,随机变量X的取值就越稳定,波动就越小.
(4)标准差与随机变量本身有相同的单位,所以在实际问题中应
用更广泛.
(5)方差也可用公式D(X)=E(X2)-(E(X))2计算(可由
·pi展开整理得).
2.随机变量的方差和样本方差之间的关系
区别
随机变量的方差是常数,而样本的方差是随着样本的不同而变化的,因此样本的方差是随机变量
联系
对于简单随机样本,随着样本容量的增加,样本方差越来越接近总体方差,因此常用样本方差来估计总体方差
3.方差具有的性质
当a,b均为常数时,随机变量η=aξ+b的方差D(η)=D(aξ+b)=a2D(ξ).特别地:
(1)当a=0时,D(b)=0,即常数的方差等于0.
(2)当a=1时,D(ξ+b)=D(ξ),即随机变量与常数之和的方差等于这个随机变量的方差本身.
(3)当b=0时,D(aξ)=a2D(ξ),即随机变量与常数之积的方差,等于这个常数的平方与这个随机变量方差的乘积.
(4)当a,b均为非零常数时,随机变量η=aξ+b的方差D(η)=D(aξ+b)=a2D(ξ).
【知识拓展】证明公式D(X)=E(X2)-(E(X))2
证明:D(X)=(x1-E(X))2p1+(x2-E(X))2p2+…+(xn-E(X))2pn
=( p1+ p2+…+ pn)-2E(X)(x1p1+x2p2+…+xnpn)
+(E(X))2(p1+p2+…+pn)
=E(X2)-2(E(X))2+(E(X))2
=E(X2)-((E(X))2.
利用公式D(X)=E(X2)-(E(X))2可以简化求方差的过程.
【微思考】
(1)数学期望与方差表示的含义相同吗?
提示:不同.数学期望是概率意义下的平均值,而方差体现了随机变量偏离于期望的平均程度.
(2)两点分布的方差同二项分布的方差存在什么关系?
提示:由于两点分布是特殊的二项分布,故两点分布的方差同二项分布的方差存在特殊与一般的关系.
【即时练】
(2014·杭州高二检测)某班从4名男生、2名女生中选出3人参加志愿者服务,若选出的男生人数为ξ,则ξ的方差D(ξ)=
.
【解析】依题意得,随机变量ξ服从超几何分布,
随机变量ξ表示其中男生的人数,ξ可能取的值为1,2,3.
所以X的分布列为:
由分布列可知E(ξ)= =2,
又E(ξ2)= ,
所以D(ξ)=E(ξ2)-(E(ξ))2
= -22=0.4.
答案:0.4
ξ
1
2
3
P
【题型示范】
类型一 离散型随机变量的方差及标准差的计算
【典例1】
(1)同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)= ( )
(2)已知X的分布列为
设Y=2X+3.求E(Y),D(Y).
X
-1
0
1
P
【解题探究】1.题(1)中两枚硬币同时出现反面的次数ξ服从什么分布?
2.题(2)中,可以根据分布列直接计算出哪个量的期望与方差?
【探究提示】1.两枚硬币同时出现反面的次数ξ~B .
2.可以利用公式计算出E(X)与D(X).
【自主解答】(1)选A.两枚硬币同时出现反面的概率为
故ξ~B ,
因此D(ξ)=
(2)由条件中所给的随机变量的分布列可知
E(X)=
D(X)=
所以E(Y)=E(2X+3)=
D(Y)=D(2X+3)=
【延伸探究】在题(1)的条件不变的情况下,求“两枚硬币不
同时出现同面的次数η的方差”.
【解题指南】不同时出现同面的次数η~B .
【解析】不同时出现同面的概率为 .由题意可
知,同时抛掷两枚均匀的硬币10次,不同时出现同面的次数
η~B ,故D(η)= =2.5.
【方法技巧】
1.求离散型随机变量的方差的类型及解决方法
(1)已知分布列型(非两点分布或二项分布):直接利用定
义求解,先求均值,再求方差.
(2)已知分布列是两点分布或二项分布型:直接套用公式求解,具体如下,
①若X服从两点分布,则D(X)=p(1-p).
②若X~B(n,p),则D(X)=np(1-p).
(3)未知分布列型:求解时可先借助已知条件及概率知识先求得分布列,然后转化成(1)中的情况.
(4)对于已知D(X)求D(aX+b)型,利用方差的性质求解,即利用D(aX+b)=a2D(X)求解.
2.求离散型随机变量ξ的方差、标准差的步骤
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ), .若ξ~B(n,p),
则不必写出分布列,直接用公式计算即可.
【方法技巧】利用均值和方差的意义解决实际问题的步骤
(1)比较均值.离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等的情况下计算方差.方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论.依据均值和方差的几何意义做出结论.
谢谢!
问题
引航
1.离散型随机变量的方差及标准差的定义是什么?
2.方差具有哪些性质?两点分布与二项分布的方差分别是什么?
3.如何计算简单离散型随机变量的方差?
1.方差、标准差的定义及方差的性质
(1)方差及标准差的定义:
设离散型随机变量X的分布列为
①方差D(X)=______________.
②标准差为______.
(2)方差的性质:D(aX+b)=______.
X
x1
x2
…
xi
…
xn
P
p1
p2
…
pi
…
pn
a2D(X)
2.两个常见分布的方差
(1)若X服从两点分布,则D(X)=_______.
(2)若X~B(n,p),则D(X)=________.
p(1-p)
np(1-p)
1.判一判(正确的打“√”,错误的打“×”)
(1)离散型随机变量的方差越大,随机变量越稳定. ( )
(2)若a是常数,则D(a)=0. ( )
(3)离散型随机变量的方差反映了随机变量偏离于期望的平均程度. ( )
【解析】(1)错误.离散型随机变量的方差越大,随机变量越不稳定.
(2)正确.因为E(a)=a,所以D(a)=0.
(3)正确.由离散型随机变量的方差的几何意义可知,其反映了随机变量偏离于期望的平均程度.
答案:(1)× (2)√ (3)√
2.做一做(请把正确的答案写在横线上)
(1)若随机变量X服从两点分布,且成功的概率p=0.5,则E(X)和
D(X)分别为 .
(2)设随机变量ξ~B ,则D(ξ)= .
(3)如果X是离散型随机变量,Y=3X+2,那么D(Y)= D(X).
【解析】(1)因为X服从两点分布,
所以X的概率分布为
所以E(X)=0×0.5+1×0.5=0.5,
D(X)=0.52×0.5+(1-0.5)2×0.5=0.25.
答案:0.5和0.25
X
0
1
P
0.5
0.5
(2)因为随机变量ξ~B ,
所以D(ξ)=
答案:
(3)由于X是离散型随机变量,Y=3X+2呈线性关系,代入公式,则
E(Y)=3E(X)+2,D(Y)=32D(X)=9D(X).
答案:9
【要点探究】
知识点 方差、标准差的定义及方差的性质
1.对随机变量X的方差、标准差的五点说明
(1)随机变量X的方差的定义与一组数据的方差的定义是相同的.
(2)随机变量X的方差和标准差都反映了随机变量X取值的稳定性和波动、集中与离散程度.
(3)D(X)越小,随机变量X的取值就越稳定,波动就越小.
(4)标准差与随机变量本身有相同的单位,所以在实际问题中应
用更广泛.
(5)方差也可用公式D(X)=E(X2)-(E(X))2计算(可由
·pi展开整理得).
2.随机变量的方差和样本方差之间的关系
区别
随机变量的方差是常数,而样本的方差是随着样本的不同而变化的,因此样本的方差是随机变量
联系
对于简单随机样本,随着样本容量的增加,样本方差越来越接近总体方差,因此常用样本方差来估计总体方差
3.方差具有的性质
当a,b均为常数时,随机变量η=aξ+b的方差D(η)=D(aξ+b)=a2D(ξ).特别地:
(1)当a=0时,D(b)=0,即常数的方差等于0.
(2)当a=1时,D(ξ+b)=D(ξ),即随机变量与常数之和的方差等于这个随机变量的方差本身.
(3)当b=0时,D(aξ)=a2D(ξ),即随机变量与常数之积的方差,等于这个常数的平方与这个随机变量方差的乘积.
(4)当a,b均为非零常数时,随机变量η=aξ+b的方差D(η)=D(aξ+b)=a2D(ξ).
【知识拓展】证明公式D(X)=E(X2)-(E(X))2
证明:D(X)=(x1-E(X))2p1+(x2-E(X))2p2+…+(xn-E(X))2pn
=( p1+ p2+…+ pn)-2E(X)(x1p1+x2p2+…+xnpn)
+(E(X))2(p1+p2+…+pn)
=E(X2)-2(E(X))2+(E(X))2
=E(X2)-((E(X))2.
利用公式D(X)=E(X2)-(E(X))2可以简化求方差的过程.
【微思考】
(1)数学期望与方差表示的含义相同吗?
提示:不同.数学期望是概率意义下的平均值,而方差体现了随机变量偏离于期望的平均程度.
(2)两点分布的方差同二项分布的方差存在什么关系?
提示:由于两点分布是特殊的二项分布,故两点分布的方差同二项分布的方差存在特殊与一般的关系.
【即时练】
(2014·杭州高二检测)某班从4名男生、2名女生中选出3人参加志愿者服务,若选出的男生人数为ξ,则ξ的方差D(ξ)=
.
【解析】依题意得,随机变量ξ服从超几何分布,
随机变量ξ表示其中男生的人数,ξ可能取的值为1,2,3.
所以X的分布列为:
由分布列可知E(ξ)= =2,
又E(ξ2)= ,
所以D(ξ)=E(ξ2)-(E(ξ))2
= -22=0.4.
答案:0.4
ξ
1
2
3
P
【题型示范】
类型一 离散型随机变量的方差及标准差的计算
【典例1】
(1)同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)= ( )
(2)已知X的分布列为
设Y=2X+3.求E(Y),D(Y).
X
-1
0
1
P
【解题探究】1.题(1)中两枚硬币同时出现反面的次数ξ服从什么分布?
2.题(2)中,可以根据分布列直接计算出哪个量的期望与方差?
【探究提示】1.两枚硬币同时出现反面的次数ξ~B .
2.可以利用公式计算出E(X)与D(X).
【自主解答】(1)选A.两枚硬币同时出现反面的概率为
故ξ~B ,
因此D(ξ)=
(2)由条件中所给的随机变量的分布列可知
E(X)=
D(X)=
所以E(Y)=E(2X+3)=
D(Y)=D(2X+3)=
【延伸探究】在题(1)的条件不变的情况下,求“两枚硬币不
同时出现同面的次数η的方差”.
【解题指南】不同时出现同面的次数η~B .
【解析】不同时出现同面的概率为 .由题意可
知,同时抛掷两枚均匀的硬币10次,不同时出现同面的次数
η~B ,故D(η)= =2.5.
【方法技巧】
1.求离散型随机变量的方差的类型及解决方法
(1)已知分布列型(非两点分布或二项分布):直接利用定
义求解,先求均值,再求方差.
(2)已知分布列是两点分布或二项分布型:直接套用公式求解,具体如下,
①若X服从两点分布,则D(X)=p(1-p).
②若X~B(n,p),则D(X)=np(1-p).
(3)未知分布列型:求解时可先借助已知条件及概率知识先求得分布列,然后转化成(1)中的情况.
(4)对于已知D(X)求D(aX+b)型,利用方差的性质求解,即利用D(aX+b)=a2D(X)求解.
2.求离散型随机变量ξ的方差、标准差的步骤
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ), .若ξ~B(n,p),
则不必写出分布列,直接用公式计算即可.
【方法技巧】利用均值和方差的意义解决实际问题的步骤
(1)比较均值.离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等的情况下计算方差.方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论.依据均值和方差的几何意义做出结论.
谢谢!
同课章节目录
