8.3正态分布曲线课件-湘教版数学选修2-3(27张PPT)
文档属性
| 名称 | 8.3正态分布曲线课件-湘教版数学选修2-3(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:49:23 | ||
图片预览


文档简介
正态分布曲线
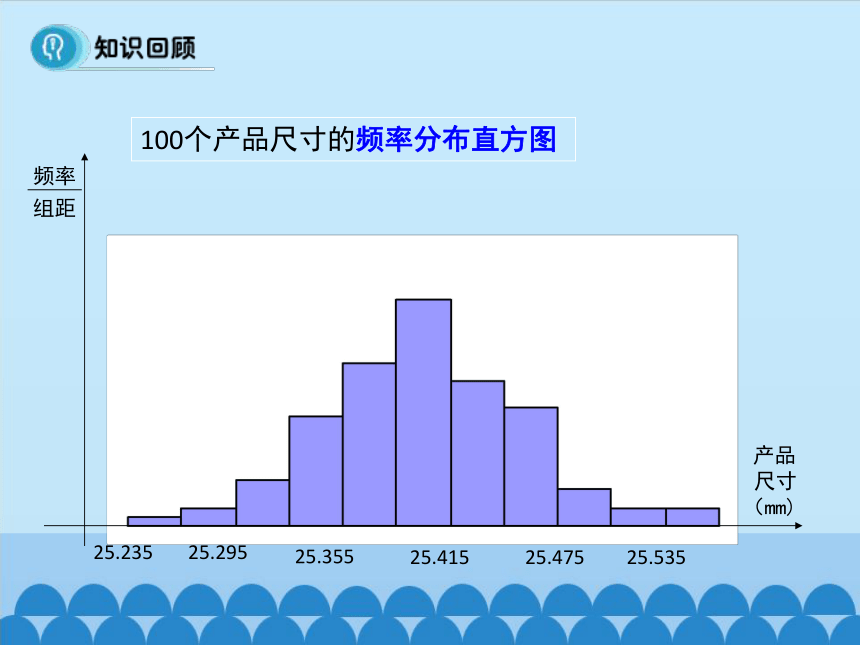
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
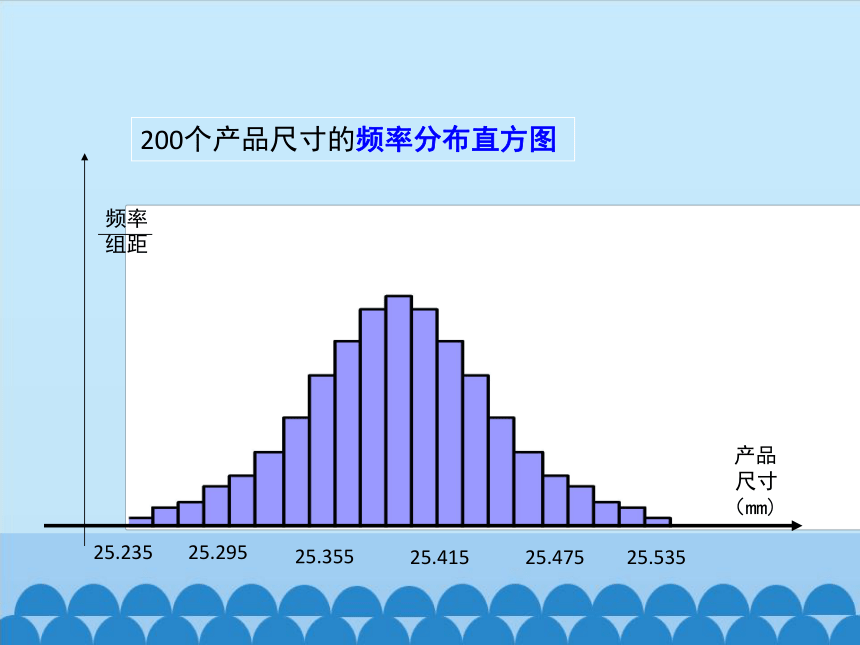
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
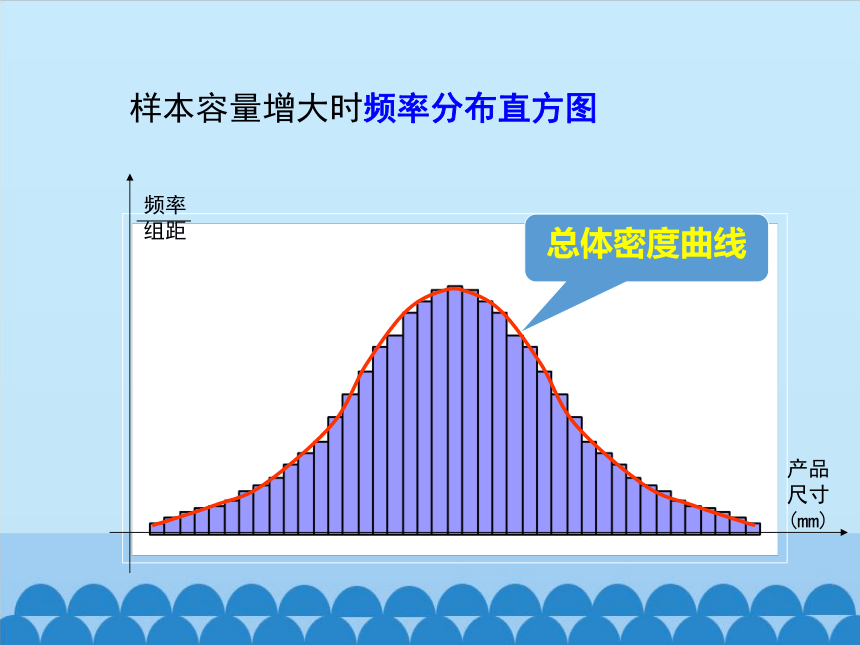
样本容量增大时频率分布直方图
频率
组距
产品
尺寸
(mm)
总体密度曲线
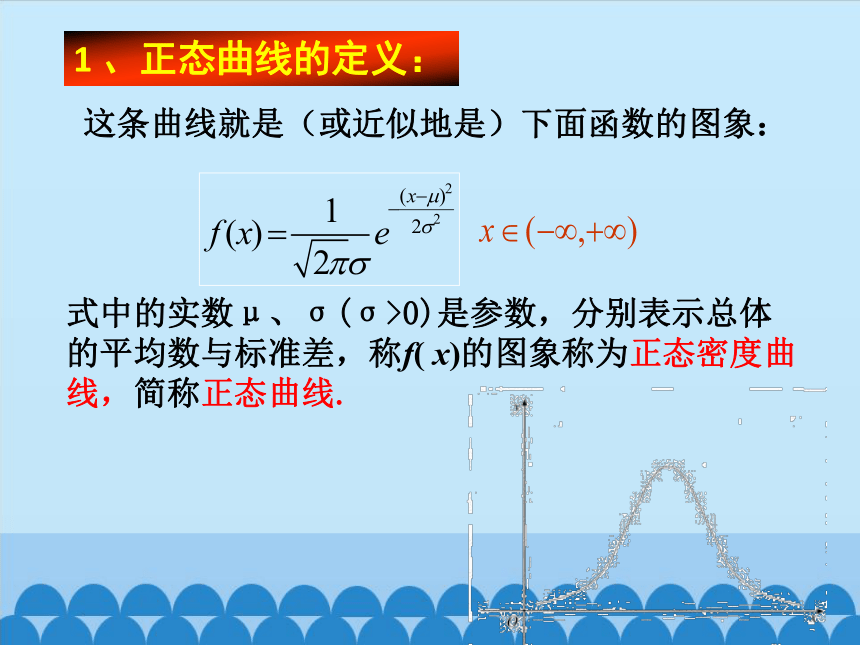
1 、正态曲线的定义:
式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差,称f( x)的图象称为正态密度曲线,简称正态曲线.
这条曲线就是(或近似地是)下面函数的图象:
组距
频率
组距
o
2
4
6
8
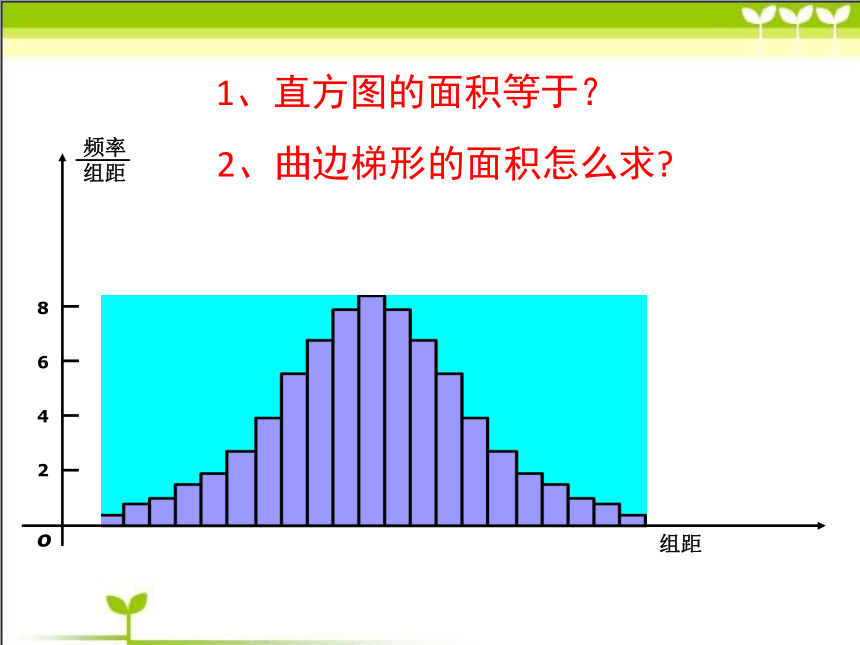
1、直方图的面积等于?
2、曲边梯形的面积怎么求?
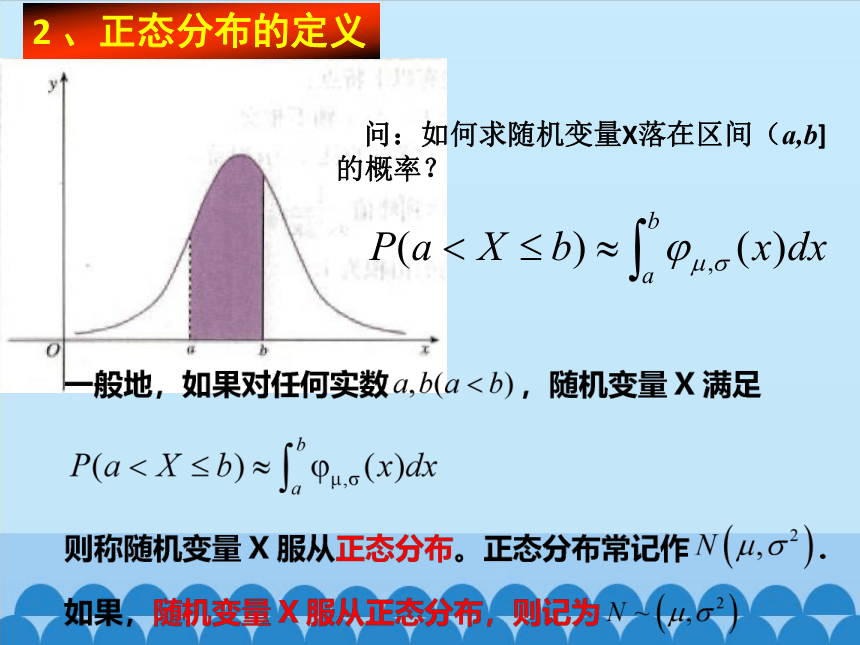
2 、正态分布的定义
问:如何求随机变量X落在区间(a,b]的概率?
正态分布存在于自然现象、生产和生活实际之中.在概率和统计中占有重要的地位.
μ
(-∞,μ]
(μ,+∞)
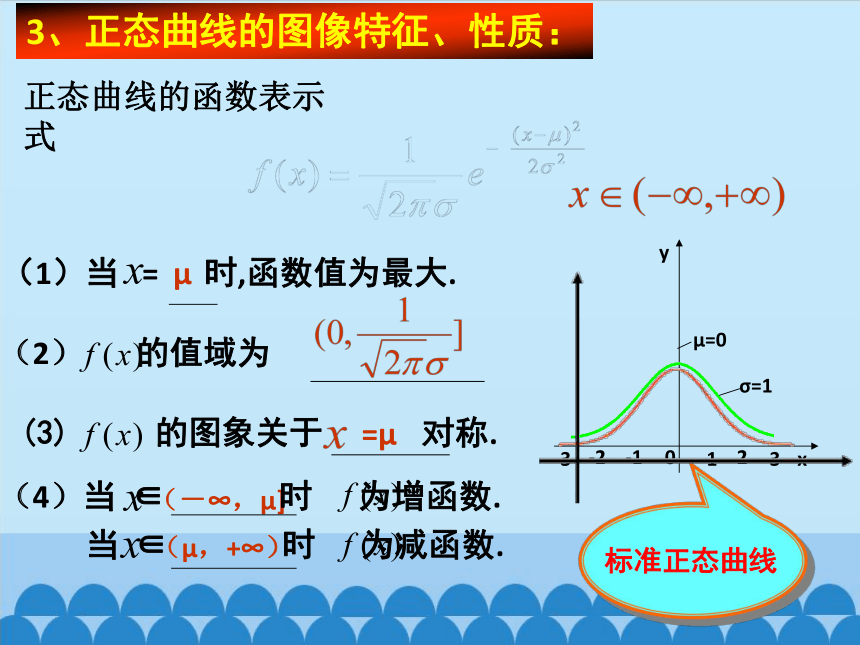
(1)当 = 时,函数值为最大.
(3) 的图象关于 对称.
(2) 的值域为
(4)当 ∈ 时 为增函数.
当 ∈ 时 为减函数.
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
=μ
3、正态曲线的图像特征、性质:
正态曲线的函数表示式
课堂练习
书本75页 A组 第1题
20
25
30
15
10
x
y
5
35
2、如图,是一个正态曲线,试根据图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差。
练习册例1
正态密度曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(3)曲线在x=μ处达到峰值(最高点)
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
x=m
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
x=m
x=m
(4)曲线与x轴之间的面积为1
?3
?1
?2
σ=0.5
μ= -1
μ=0
μ= 1
正态密度曲线的图像特征
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴移动
?
?=0.5
?=1
?=2
μ=0
正态密度曲线的图像特征
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
3、正态分布的概率计算
【解】 (1)由于X~N(2,σ2),对称轴x=2,画出示意图,
∵P(0 ∴P(0 =2×0.2=0.4
(2)P(X>4)=[1-P(0 =(1-0.4)=0.3
C
利用对称性来求概率
3、正态分布的3σ原则
正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.26%,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量只取 之间的值,并称为3σ原则.
4、正态分布的应用
2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则
= =
4、若X~N(5,1),求P(6D
0.5
0.9544
练习:1、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内?( )
(90,110] B.(95,125] C.(100,120] D.(105,115]
C
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
样本容量增大时频率分布直方图
频率
组距
产品
尺寸
(mm)
总体密度曲线
1 、正态曲线的定义:
式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差,称f( x)的图象称为正态密度曲线,简称正态曲线.
这条曲线就是(或近似地是)下面函数的图象:
组距
频率
组距
o
2
4
6
8
1、直方图的面积等于?
2、曲边梯形的面积怎么求?
2 、正态分布的定义
问:如何求随机变量X落在区间(a,b]的概率?
正态分布存在于自然现象、生产和生活实际之中.在概率和统计中占有重要的地位.
μ
(-∞,μ]
(μ,+∞)
(1)当 = 时,函数值为最大.
(3) 的图象关于 对称.
(2) 的值域为
(4)当 ∈ 时 为增函数.
当 ∈ 时 为减函数.
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
=μ
3、正态曲线的图像特征、性质:
正态曲线的函数表示式
课堂练习
书本75页 A组 第1题
20
25
30
15
10
x
y
5
35
2、如图,是一个正态曲线,试根据图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差。
练习册例1
正态密度曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(3)曲线在x=μ处达到峰值(最高点)
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
x=m
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
x=m
x=m
(4)曲线与x轴之间的面积为1
?3
?1
?2
σ=0.5
μ= -1
μ=0
μ= 1
正态密度曲线的图像特征
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴移动
?
?=0.5
?=1
?=2
μ=0
正态密度曲线的图像特征
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
3、正态分布的概率计算
【解】 (1)由于X~N(2,σ2),对称轴x=2,画出示意图,
∵P(0
(2)P(X>4)=[1-P(0
C
利用对称性来求概率
3、正态分布的3σ原则
正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.26%,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量只取 之间的值,并称为3σ原则.
4、正态分布的应用
2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则
= =
4、若X~N(5,1),求P(6
0.5
0.9544
练习:1、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内?( )
(90,110] B.(95,125] C.(100,120] D.(105,115]
C
同课章节目录
