8.4列联表独立性分析案例课件-湘教版数学选修2-3(19张PPT)
文档属性
| 名称 | 8.4列联表独立性分析案例课件-湘教版数学选修2-3(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:52:24 | ||
图片预览


文档简介
§8.4 列联表独立性分析案例
引例:甲乙二人玩掷硬币的游戏:正面向上,甲赢; 反面向上,乙赢。
他们玩了6局,结果都是甲赢。乙认为甲有作弊行为,游戏不公平。
你认为这游戏公平吗?
假设:游戏公平
“甲6局都赢”的概率为 :
(“甲6局都赢”为小概率事件,
在一次实验中几乎不发生)
所以:拒绝假设,即游戏不公平
这种判断有可能犯错误?
假设检验
§8.4 列联表独立性分析
案例
案例
这与条件“甲6局都赢”相矛盾
*
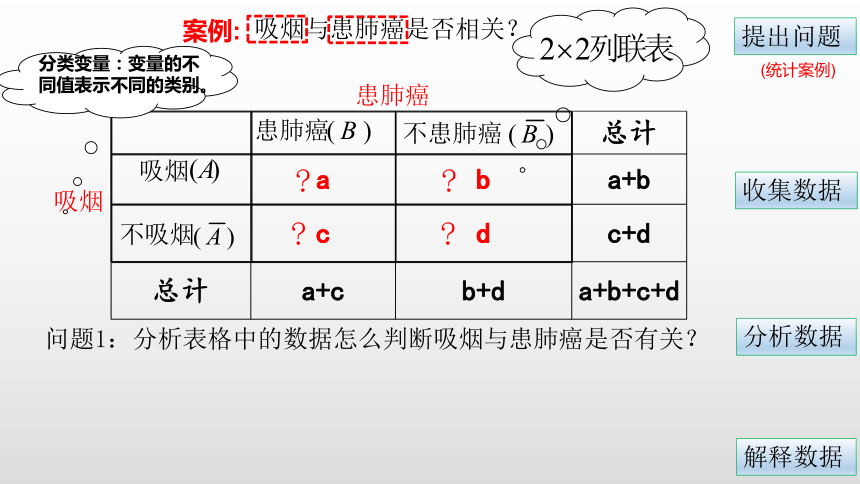
吸烟与患肺癌是否相关?
吸烟
患肺癌
吸烟
不吸烟
患肺癌
不患肺癌
?
?
?
?
提出问题
收集数据
分析数据
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
a
b
c
d
问题1:分析表格中的数据怎么判断吸烟与患肺癌是否有关?
解释数据
(统计案例)
分类变量:变量的不同值表示不同的类别。
案例:
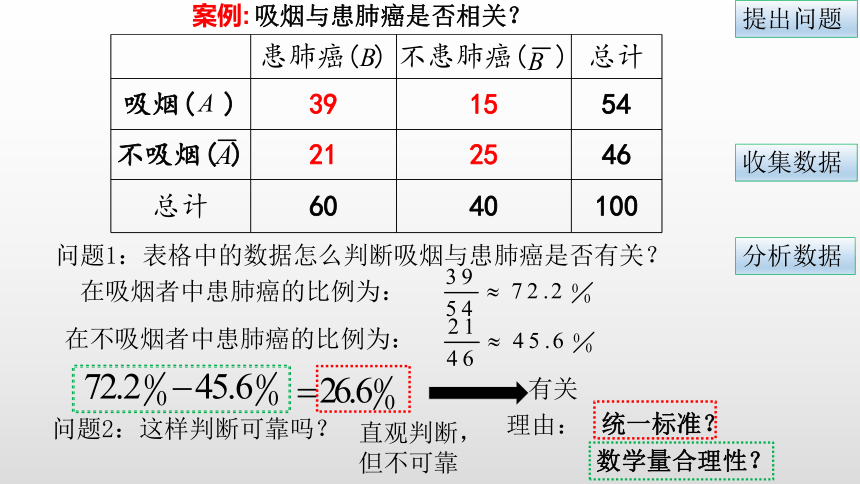
吸烟与患肺癌是否相关?
患肺癌( )
不患肺癌( )
总计
吸烟( )
39
15
54
不吸烟( )
21
25
46
总计
60
40
100
问题1:表格中的数据怎么判断吸烟与患肺癌是否有关?
在吸烟者中患肺癌的比例为:
在不吸烟者中患肺癌的比例为:
统一标准?
有关
问题2:这样判断可靠吗?
直观判断,
但不可靠
理由:
数学量合理性?
提出问题
收集数据
分析数据
案例:
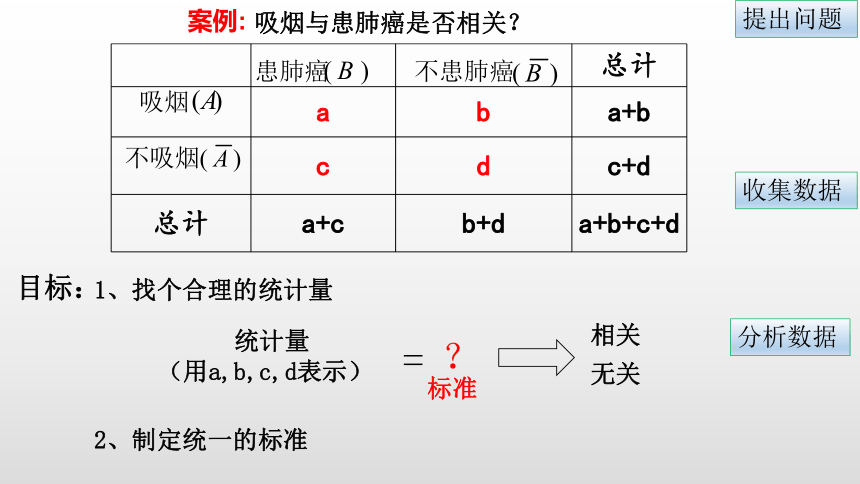
吸烟与患肺癌是否相关?
吸烟
不吸烟
患肺癌
不患肺癌
提出问题
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
统计量
(用a,b,c,d表示)
=
相关
无关
?
目标:
1、找个合理的统计量
2、制定统一的标准
标准
提出问题
收集数据
分析数据
案例:
吸烟与患肺癌是否相关?
案例:
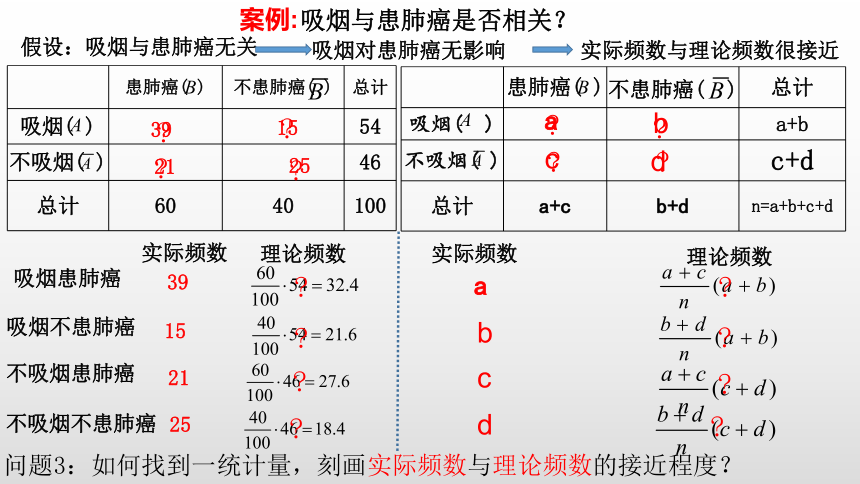
假设:吸烟与患肺癌无关
实际频数与理论频数很接近
吸烟对患肺癌无影响
患肺癌( )
不患肺癌( )
总计
吸烟( )
a+b
不吸烟( )
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
54
不吸烟( )
46
总计
60
40
100
39
21
15
25
?
?
?
?
实际频数
吸烟患肺癌
吸烟不患肺癌
理论频数
a
b
c
d
实际频数
39
15
21
25
理论频数
不吸烟患肺癌
不吸烟不患肺癌
问题3:如何找到一统计量,刻画实际频数与理论频数的接近程度?
?
?
?
?
?
?
?
?
a
b
c
d
?
?
?
?
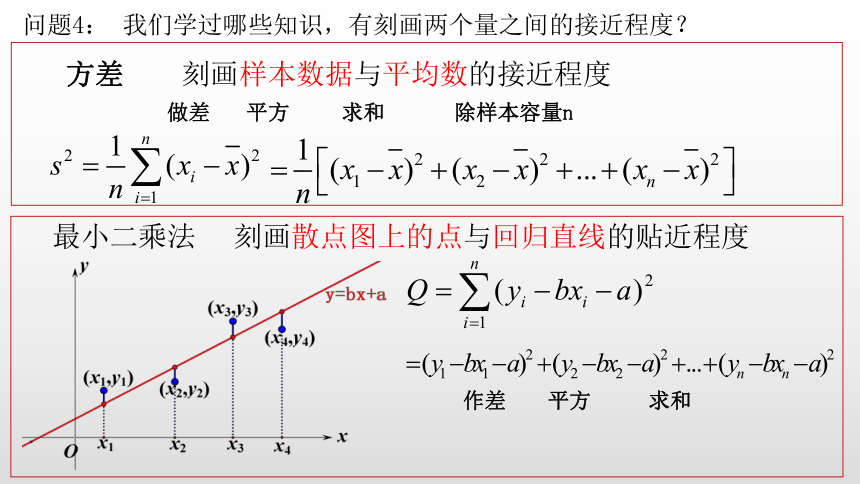
问题4: 我们学过哪些知识,有刻画两个量之间的接近程度?
方差
刻画样本数据与平均数的接近程度
做差
平方
求和
除样本容量n
最小二乘法
刻画散点图上的点与回归直线的贴近程度
作差
平方
求和
吸烟与患肺癌是否相关?
案例:
假设:吸烟与患肺癌无关
实际频数与理论频数很接近
吸烟对患肺癌无影响
患肺癌( )
不患肺癌( )
总计
吸烟( )
a+b
不吸烟( )
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
54
不吸烟( )
46
总计
60
40
100
39
21
15
25
实际频数
吸烟患肺癌
吸烟不患肺癌
理论频数
a
b
c
d
实际频数
39
15
21
25
理论频数
不吸烟患肺癌
不吸烟不患肺癌
问题3:如何找到一统计量,刻画实际频数与理论频数的接近程度?
a
b
c
d
作差
平方
求和
除以理论频数
化简后,得
卡方
患肺癌( )
不患肺癌( )
总计
吸烟( )
a
b
a+b
不吸烟( )
c
d
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
39
15
54
不吸烟( )
21
25
46
总计
60
40
100
吸烟与患肺癌是否相关?
吸烟
不吸烟
患肺癌
不患肺癌
提出问题
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
目标:
1、找个合理的统计量
2、找个统一的标准
提出问题
收集数据
分析数据
案例:
卡方
相关
无关
?
=
标准
假设:吸烟与患肺癌无关
皮尔逊(Karl Pearson,1857 —1936),
英国统计学家.现代统计学的创始
人之一,被誉为统计学之父.
问题5:如何制定统一标准,判断吸烟与患肺癌是否相关?
假设:吸烟 和患肺癌无关
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
小概率
相关
无关
所以:拒绝假设,即吸烟和患肺癌有关
在犯错为1%的前提下,吸烟和患肺癌有关
有99%把握认为吸烟和患肺癌有关
(小概率事件,拒绝假设)
没有充分的理由判断相关,
也不能判断无关
独立性检验:利用随机变量 来确定有多大程度上可以认为“两个分类变量有关系”的方法
为小概率事件,在一次实验中几乎不发生
这与假设条件下 相矛盾
( 不是小概率事件,
不能拒绝假设,也不能支持假设)
问题6:根据以上分析,你能总结出独立性检验的一般步骤吗?
假设:吸烟与患肺癌无关
在犯错为1%的前提下,吸烟和患肺癌有关
有99%把握认为吸烟和患肺癌有关
假设:两变量无关
查临界值表
下结论
案例:
案例:
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
有99.9%把握
认为A与B有关
有99%把握
认为A与B有关
有95%的把握
认为A与B有关
在犯错误5%的前提下 认为A与B有关
没有充分的依据显示A与B有关,但也不能显示A与B无关
假设:A 和B无关
小概率
在犯错误1%的前提下 认为A与B有关
在犯错误0.1%的前提下认为A与B有关
问题7:独立性检验与反证法的联系与区别?
(假设检验)
独立性检验
反证法
假设
假设
推出矛盾
推出矛盾
两分类变量无关
结论反面成立
小概率事件
与公理、定理、已知等矛盾
拒绝假设
拒绝假设
这种推断有可能犯错误
这种推断
不会犯错误
通过随机询问某校100名高中学生在购买食物时是否看营养说明,得到如下的列联表,问:“性别”与“是否看营养说明”有关吗?
看营养说明
不看营养说明
总计
男
10
20
30
女
40
30
70
总计
50
50
100
例题
解:假设“性别”与“是否看营养说明”无关
由临界值表得:
所以,在犯错为5%的前提下,认为“性别”与“是否看营养说明”有关;
有99%把握认为“性别”与“是否看营养说明”有关
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
课后作业
为了解新高考改革学生选修物理情况,试对我校高一学生选修物理课程情况进行调查,用卡方独立性检验分析,研究选修物理是否与性别有关?
有一个颠扑不破的真理,那就是当我们不能确定什么是真的时,我们就应该去探求什么是最可能的。
笛卡尔
寄语
*
引例:甲乙二人玩掷硬币的游戏:正面向上,甲赢; 反面向上,乙赢。
他们玩了6局,结果都是甲赢。乙认为甲有作弊行为,游戏不公平。
你认为这游戏公平吗?
假设:游戏公平
“甲6局都赢”的概率为 :
(“甲6局都赢”为小概率事件,
在一次实验中几乎不发生)
所以:拒绝假设,即游戏不公平
这种判断有可能犯错误?
假设检验
§8.4 列联表独立性分析
案例
案例
这与条件“甲6局都赢”相矛盾
*
吸烟与患肺癌是否相关?
吸烟
患肺癌
吸烟
不吸烟
患肺癌
不患肺癌
?
?
?
?
提出问题
收集数据
分析数据
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
a
b
c
d
问题1:分析表格中的数据怎么判断吸烟与患肺癌是否有关?
解释数据
(统计案例)
分类变量:变量的不同值表示不同的类别。
案例:
吸烟与患肺癌是否相关?
患肺癌( )
不患肺癌( )
总计
吸烟( )
39
15
54
不吸烟( )
21
25
46
总计
60
40
100
问题1:表格中的数据怎么判断吸烟与患肺癌是否有关?
在吸烟者中患肺癌的比例为:
在不吸烟者中患肺癌的比例为:
统一标准?
有关
问题2:这样判断可靠吗?
直观判断,
但不可靠
理由:
数学量合理性?
提出问题
收集数据
分析数据
案例:
吸烟与患肺癌是否相关?
吸烟
不吸烟
患肺癌
不患肺癌
提出问题
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
统计量
(用a,b,c,d表示)
=
相关
无关
?
目标:
1、找个合理的统计量
2、制定统一的标准
标准
提出问题
收集数据
分析数据
案例:
吸烟与患肺癌是否相关?
案例:
假设:吸烟与患肺癌无关
实际频数与理论频数很接近
吸烟对患肺癌无影响
患肺癌( )
不患肺癌( )
总计
吸烟( )
a+b
不吸烟( )
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
54
不吸烟( )
46
总计
60
40
100
39
21
15
25
?
?
?
?
实际频数
吸烟患肺癌
吸烟不患肺癌
理论频数
a
b
c
d
实际频数
39
15
21
25
理论频数
不吸烟患肺癌
不吸烟不患肺癌
问题3:如何找到一统计量,刻画实际频数与理论频数的接近程度?
?
?
?
?
?
?
?
?
a
b
c
d
?
?
?
?
问题4: 我们学过哪些知识,有刻画两个量之间的接近程度?
方差
刻画样本数据与平均数的接近程度
做差
平方
求和
除样本容量n
最小二乘法
刻画散点图上的点与回归直线的贴近程度
作差
平方
求和
吸烟与患肺癌是否相关?
案例:
假设:吸烟与患肺癌无关
实际频数与理论频数很接近
吸烟对患肺癌无影响
患肺癌( )
不患肺癌( )
总计
吸烟( )
a+b
不吸烟( )
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
54
不吸烟( )
46
总计
60
40
100
39
21
15
25
实际频数
吸烟患肺癌
吸烟不患肺癌
理论频数
a
b
c
d
实际频数
39
15
21
25
理论频数
不吸烟患肺癌
不吸烟不患肺癌
问题3:如何找到一统计量,刻画实际频数与理论频数的接近程度?
a
b
c
d
作差
平方
求和
除以理论频数
化简后,得
卡方
患肺癌( )
不患肺癌( )
总计
吸烟( )
a
b
a+b
不吸烟( )
c
d
c+d
总计
a+c
b+d
n=a+b+c+d
患肺癌( )
不患肺癌( )
总计
吸烟( )
39
15
54
不吸烟( )
21
25
46
总计
60
40
100
吸烟与患肺癌是否相关?
吸烟
不吸烟
患肺癌
不患肺癌
提出问题
总计
a
b
a+b
c
d
c+d
总计
a+c
b+d
a+b+c+d
目标:
1、找个合理的统计量
2、找个统一的标准
提出问题
收集数据
分析数据
案例:
卡方
相关
无关
?
=
标准
假设:吸烟与患肺癌无关
皮尔逊(Karl Pearson,1857 —1936),
英国统计学家.现代统计学的创始
人之一,被誉为统计学之父.
问题5:如何制定统一标准,判断吸烟与患肺癌是否相关?
假设:吸烟 和患肺癌无关
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
小概率
相关
无关
所以:拒绝假设,即吸烟和患肺癌有关
在犯错为1%的前提下,吸烟和患肺癌有关
有99%把握认为吸烟和患肺癌有关
(小概率事件,拒绝假设)
没有充分的理由判断相关,
也不能判断无关
独立性检验:利用随机变量 来确定有多大程度上可以认为“两个分类变量有关系”的方法
为小概率事件,在一次实验中几乎不发生
这与假设条件下 相矛盾
( 不是小概率事件,
不能拒绝假设,也不能支持假设)
问题6:根据以上分析,你能总结出独立性检验的一般步骤吗?
假设:吸烟与患肺癌无关
在犯错为1%的前提下,吸烟和患肺癌有关
有99%把握认为吸烟和患肺癌有关
假设:两变量无关
查临界值表
下结论
案例:
案例:
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
有99.9%把握
认为A与B有关
有99%把握
认为A与B有关
有95%的把握
认为A与B有关
在犯错误5%的前提下 认为A与B有关
没有充分的依据显示A与B有关,但也不能显示A与B无关
假设:A 和B无关
小概率
在犯错误1%的前提下 认为A与B有关
在犯错误0.1%的前提下认为A与B有关
问题7:独立性检验与反证法的联系与区别?
(假设检验)
独立性检验
反证法
假设
假设
推出矛盾
推出矛盾
两分类变量无关
结论反面成立
小概率事件
与公理、定理、已知等矛盾
拒绝假设
拒绝假设
这种推断有可能犯错误
这种推断
不会犯错误
通过随机询问某校100名高中学生在购买食物时是否看营养说明,得到如下的列联表,问:“性别”与“是否看营养说明”有关吗?
看营养说明
不看营养说明
总计
男
10
20
30
女
40
30
70
总计
50
50
100
例题
解:假设“性别”与“是否看营养说明”无关
由临界值表得:
所以,在犯错为5%的前提下,认为“性别”与“是否看营养说明”有关;
有99%把握认为“性别”与“是否看营养说明”有关
P( )
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
课后作业
为了解新高考改革学生选修物理情况,试对我校高一学生选修物理课程情况进行调查,用卡方独立性检验分析,研究选修物理是否与性别有关?
有一个颠扑不破的真理,那就是当我们不能确定什么是真的时,我们就应该去探求什么是最可能的。
笛卡尔
寄语
*
同课章节目录
