8.5一元线性回归分析案例课件-湘教版数学选修2-3(33张PPT)
文档属性
| 名称 | 8.5一元线性回归分析案例课件-湘教版数学选修2-3(33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:56:41 | ||
图片预览







文档简介
8.5一元线性回归案例
第一课时
数学3——统计内容
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
复习 变量之间的两种关系
2.相关关系—是指变量之间存在着不严格的数量依存关系,即当一个或几个相互联系的变量取一定数值时,与之相对应的另一个变量的取值是随机的,但它一般按某种规律在一定范围内变化,是一种非确定性关系。
变量之间的关系
1.函数关系—是指变量之间存在着严格的数量依
存关系,即当一个或几个变量取一定的值时,另
一个变量有唯一确定值与之相对应,是一种确定
关系。
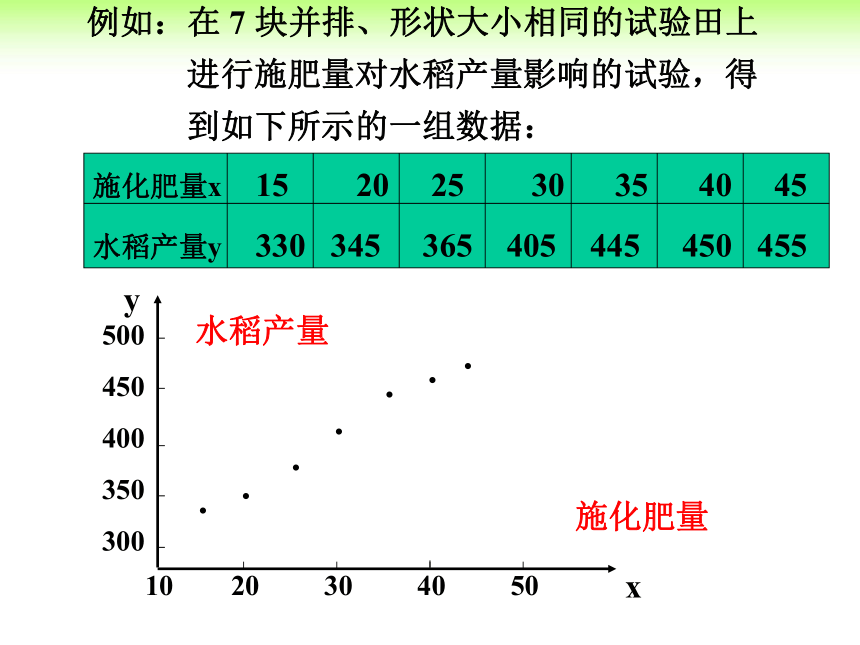
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量
水稻产量
例如:在 7 块并排、形状大小相同的试验田上
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
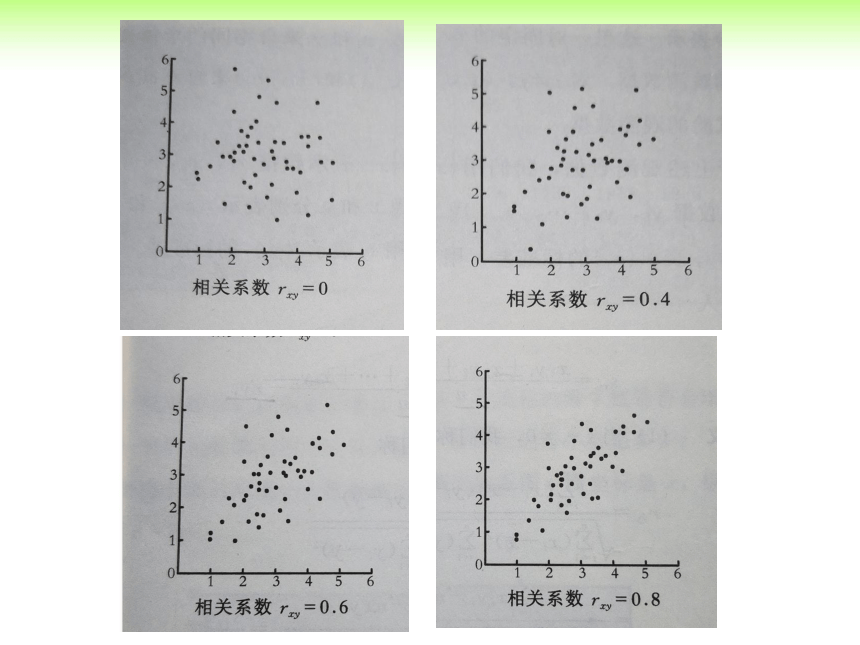
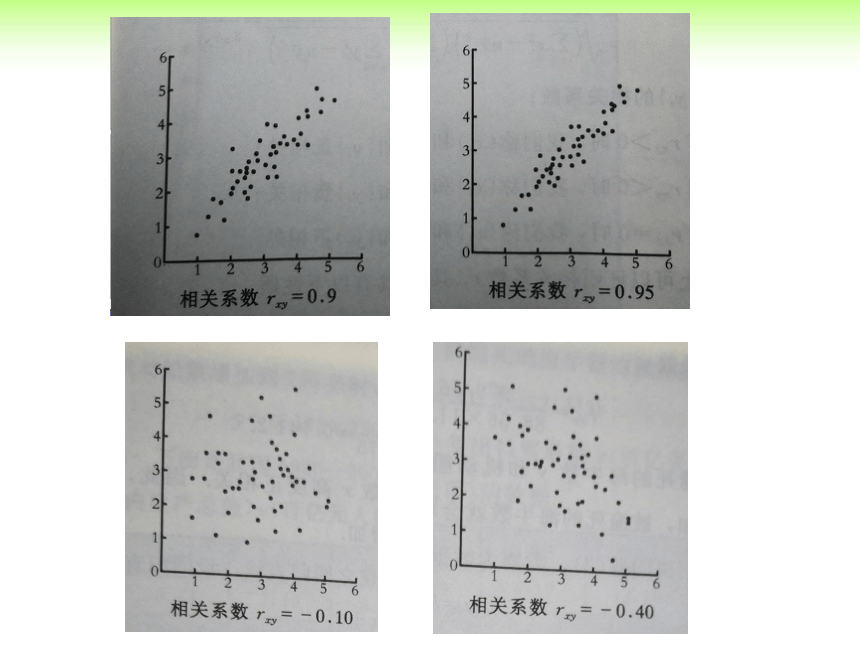
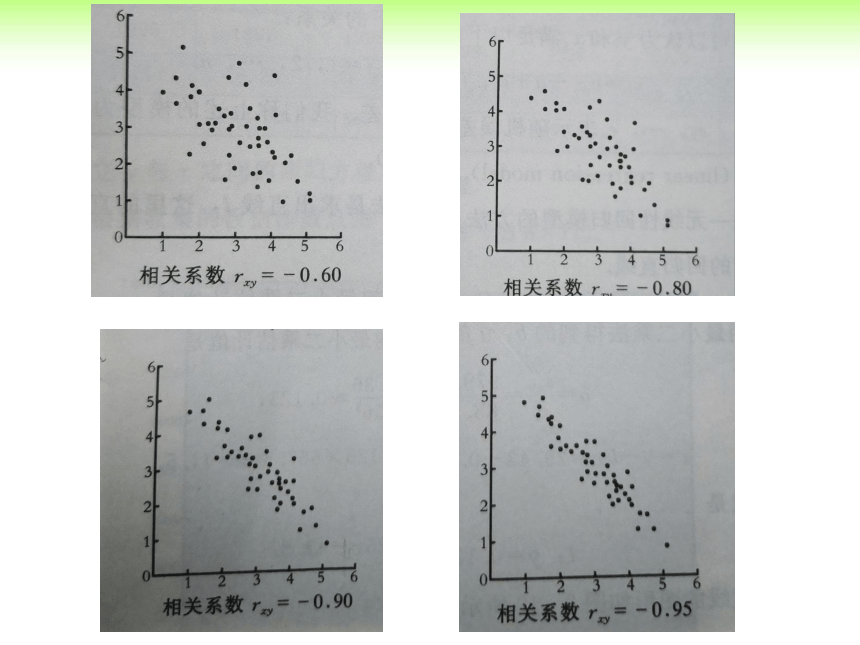
那么两个具有相关关系的变量,我们可以用什么来刻画他们之间的强弱关系?
2.如何描述两个变量之间线性相关关系的强弱?
在《必修3》中,我们简单学过用相关系数r来衡量两个
变量之间线性相关关系的方法。
相关系数r
相关系数r的性质
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
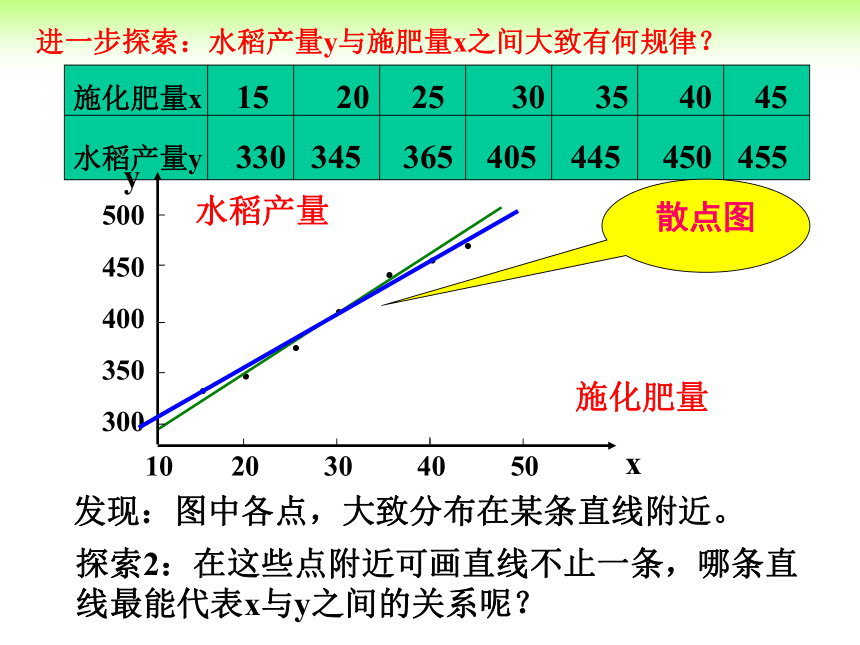
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
散点图
施化肥量
水稻产量
进一步探索:水稻产量y与施肥量x之间大致有何规律?
称为样本点的中心。
在必修3我们曾经学习过用最小二乘法求这条直线方程的斜率与截距,他们的公式分别为:
(1)、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
(2)、对两个变量进行的线性分析叫做线性回归分析。
3、回归直线方程
4、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
(5)应用:利用回归直线方程对总体进行线性相关性的检验
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
例1、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:
x(0.01%)
104
180
190
177
147
134
150
191
204
121
y(min)
100
200
210
185
155
135
170
205
235
125
(1)y与x是否具有线性相关关系;
(2)如果具有线性相关关系,求回归直线方程;
(3)预测当钢水含碳量为160个0.01%时,应冶炼多少分钟?
解:(1)列出下表,并计算
i
1
2
3
4
5
6
7
8
9
10
xi
104
180
190
177
147
134
150
191
204
121
yi
100
200
210
185
155
135
170
205
235
125
xiyi
10400
36000
39900
32745
22785
18090
25500
39155
47940
15125
所以回归直线的方程为 =1.267x-30.51
(3)当x=160时, 1.267.160-30.51=172
(2)设所求的回归方程为
答:当钢水含碳量为160个0.01%时,大概需要冶炼172分钟
1. 下表提供了某厂节能降耗技术改造后生产甲
产品过程中记录的产量x(吨)与相应的生产能耗
y(吨标准煤)的几组对照数据:
x
3
4
5
6
y
2.5
3
4
4.5
(1)请根据上表提供的数据,用最小二乘法求出
y关于x的线性回归方程y=bx+a;
(2)已知该厂技改前100吨甲产品的生产能耗为
90吨标准煤.试根据(2)求出的线性同归方程,
预测生产100吨甲产品的生产能耗比技改前降
低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。对具有相关关系的两个变量进行统计分析的方法叫回归分析。但这种统计过程中会出现一些误差。
5、回归分析
例2. 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号
1
2
3
4
5
6
7
8
身高
165
165
157
170
175
165
155
170
体重
48
57
50
54
64
61
43
59
求根据女大学生的身高预报体重的回归方程,并预报一名身高为172cm的女大学生的体重。
新问题:结合例2得出线性回归模型及随机误差,并且区分函数模型和回归模型。
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重在60.316kg左右.从散点图看到,样本点散布在某一条直线的附近,而不是在一条直线上,所以不能用一次函数y=bx+a描述它们关系.
我们可以线性回归模型来表示:y=bx+a+e,其中a和b为模型的
未知参数,e称为随机误差.
案例分析
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差.
以上三项误差越小,说明我们的回归方程的拟合效果越好,用
回归方程来预测就越准确。
我们有专门用一个量来刻画回归的拟合效果,这个量叫相关指数R2
相关指数其计算公式是
显然,当R2的值越大,说明残差所占的比例越小,回归效果约好;反之,回归效果越差.一般的,当R2越接近于1,说明解释变量和预报变量之间的相关性越强,如果同一个问题,采用不同的回归方法分析,我们可以通过选择R2大的来作为回归模型.
例3 在一段时间内,某中商品的价格x元和需求量y件之间的一组数据为:
求出y对x的回归直线方程,并说明拟合效果的好坏。
价格x
14
16
18
20
22
需求量y
12
10
7
5
3
解:
价格x
14
16
18
20
22
需求量y
12
10
7
5
3
列出相关指数的分子分母:
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
一般方法:
1.利用散点图观察两个变量是否线性相关
3.利用相关指数来判断模型拟合的效果好不好。(残差分析)
一般考到拟合效果很少用这个公式,有时候直接用绝对值来比较.
2019漳州三月市质检卷
2.利用相关系数r来说明两个变量线性相关的强弱
1) 确定解释变量和预报变量;
2) 画出散点图;
3) 确定回归方程类型;
4) 求出回归方程;
5) 利用相关指数进行残差分析,检验拟合效果.
建立回归模型的基本步骤
其中在确定回归方程类型的时候不一定用直线,如果回归方程是直线就用必修3学过的最小二乘法求出回归直线方程的斜率和截距。如果不是直线方程要学会转化。
2019厦门三月市质检卷
2019福建四月省质检卷
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
(5)应用:利用回归直线方程对总体进行线性相关性的检验
小结:求回归直线方程的步骤:
作业:
科作业纸:书P96-习题11-1
练习册:P66-67-1.2.3.4.5
P69-2.4.5.6.7
谢谢各位老师的光临指导!
第一课时
数学3——统计内容
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
复习 变量之间的两种关系
2.相关关系—是指变量之间存在着不严格的数量依存关系,即当一个或几个相互联系的变量取一定数值时,与之相对应的另一个变量的取值是随机的,但它一般按某种规律在一定范围内变化,是一种非确定性关系。
变量之间的关系
1.函数关系—是指变量之间存在着严格的数量依
存关系,即当一个或几个变量取一定的值时,另
一个变量有唯一确定值与之相对应,是一种确定
关系。
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量
水稻产量
例如:在 7 块并排、形状大小相同的试验田上
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
那么两个具有相关关系的变量,我们可以用什么来刻画他们之间的强弱关系?
2.如何描述两个变量之间线性相关关系的强弱?
在《必修3》中,我们简单学过用相关系数r来衡量两个
变量之间线性相关关系的方法。
相关系数r
相关系数r的性质
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
散点图
施化肥量
水稻产量
进一步探索:水稻产量y与施肥量x之间大致有何规律?
称为样本点的中心。
在必修3我们曾经学习过用最小二乘法求这条直线方程的斜率与截距,他们的公式分别为:
(1)、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
(2)、对两个变量进行的线性分析叫做线性回归分析。
3、回归直线方程
4、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
(5)应用:利用回归直线方程对总体进行线性相关性的检验
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
例1、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:
x(0.01%)
104
180
190
177
147
134
150
191
204
121
y(min)
100
200
210
185
155
135
170
205
235
125
(1)y与x是否具有线性相关关系;
(2)如果具有线性相关关系,求回归直线方程;
(3)预测当钢水含碳量为160个0.01%时,应冶炼多少分钟?
解:(1)列出下表,并计算
i
1
2
3
4
5
6
7
8
9
10
xi
104
180
190
177
147
134
150
191
204
121
yi
100
200
210
185
155
135
170
205
235
125
xiyi
10400
36000
39900
32745
22785
18090
25500
39155
47940
15125
所以回归直线的方程为 =1.267x-30.51
(3)当x=160时, 1.267.160-30.51=172
(2)设所求的回归方程为
答:当钢水含碳量为160个0.01%时,大概需要冶炼172分钟
1. 下表提供了某厂节能降耗技术改造后生产甲
产品过程中记录的产量x(吨)与相应的生产能耗
y(吨标准煤)的几组对照数据:
x
3
4
5
6
y
2.5
3
4
4.5
(1)请根据上表提供的数据,用最小二乘法求出
y关于x的线性回归方程y=bx+a;
(2)已知该厂技改前100吨甲产品的生产能耗为
90吨标准煤.试根据(2)求出的线性同归方程,
预测生产100吨甲产品的生产能耗比技改前降
低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。对具有相关关系的两个变量进行统计分析的方法叫回归分析。但这种统计过程中会出现一些误差。
5、回归分析
例2. 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号
1
2
3
4
5
6
7
8
身高
165
165
157
170
175
165
155
170
体重
48
57
50
54
64
61
43
59
求根据女大学生的身高预报体重的回归方程,并预报一名身高为172cm的女大学生的体重。
新问题:结合例2得出线性回归模型及随机误差,并且区分函数模型和回归模型。
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重在60.316kg左右.从散点图看到,样本点散布在某一条直线的附近,而不是在一条直线上,所以不能用一次函数y=bx+a描述它们关系.
我们可以线性回归模型来表示:y=bx+a+e,其中a和b为模型的
未知参数,e称为随机误差.
案例分析
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差.
以上三项误差越小,说明我们的回归方程的拟合效果越好,用
回归方程来预测就越准确。
我们有专门用一个量来刻画回归的拟合效果,这个量叫相关指数R2
相关指数其计算公式是
显然,当R2的值越大,说明残差所占的比例越小,回归效果约好;反之,回归效果越差.一般的,当R2越接近于1,说明解释变量和预报变量之间的相关性越强,如果同一个问题,采用不同的回归方法分析,我们可以通过选择R2大的来作为回归模型.
例3 在一段时间内,某中商品的价格x元和需求量y件之间的一组数据为:
求出y对x的回归直线方程,并说明拟合效果的好坏。
价格x
14
16
18
20
22
需求量y
12
10
7
5
3
解:
价格x
14
16
18
20
22
需求量y
12
10
7
5
3
列出相关指数的分子分母:
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
一般方法:
1.利用散点图观察两个变量是否线性相关
3.利用相关指数来判断模型拟合的效果好不好。(残差分析)
一般考到拟合效果很少用这个公式,有时候直接用绝对值来比较.
2019漳州三月市质检卷
2.利用相关系数r来说明两个变量线性相关的强弱
1) 确定解释变量和预报变量;
2) 画出散点图;
3) 确定回归方程类型;
4) 求出回归方程;
5) 利用相关指数进行残差分析,检验拟合效果.
建立回归模型的基本步骤
其中在确定回归方程类型的时候不一定用直线,如果回归方程是直线就用必修3学过的最小二乘法求出回归直线方程的斜率和截距。如果不是直线方程要学会转化。
2019厦门三月市质检卷
2019福建四月省质检卷
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
(5)应用:利用回归直线方程对总体进行线性相关性的检验
小结:求回归直线方程的步骤:
作业:
科作业纸:书P96-习题11-1
练习册:P66-67-1.2.3.4.5
P69-2.4.5.6.7
谢谢各位老师的光临指导!
同课章节目录
