苏科版八年级数学上册1.3探索全等三角形的条件一课一练习题2(Word版,解答题,含答案)
文档属性
| 名称 | 苏科版八年级数学上册1.3探索全等三角形的条件一课一练习题2(Word版,解答题,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 831.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 21:32:22 | ||
图片预览



文档简介
1.3《探索全等三角形的条件》习题2
一、解答题
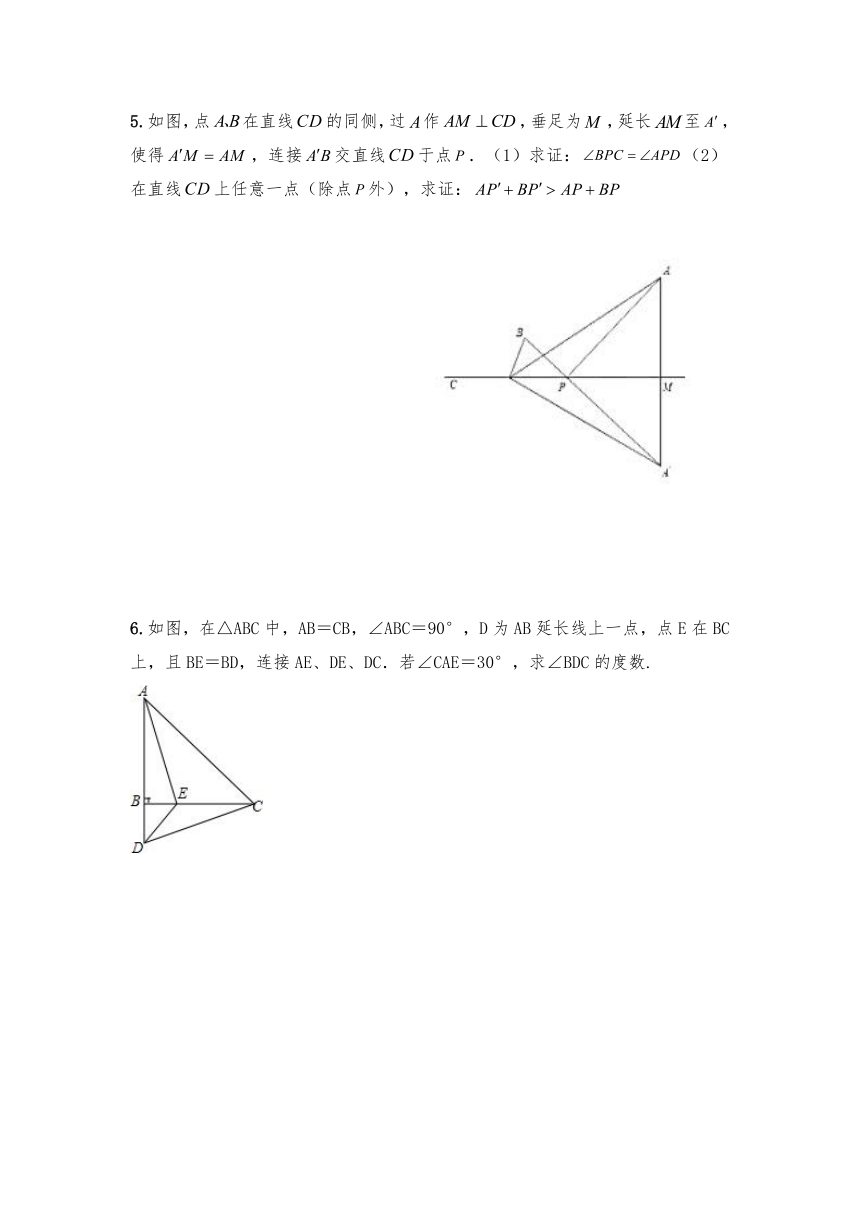
1.如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.
(1)说明△ACD与△BEC全等的理由;(2)说明AB=AD+BE的理由.
2.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,
∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.
3.综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
……
(将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.
4.已知:BE⊥CD于E,BE=DE,BC=DA,(1)求证:△BEC≌△DEA;(2)求证:BC⊥FD.
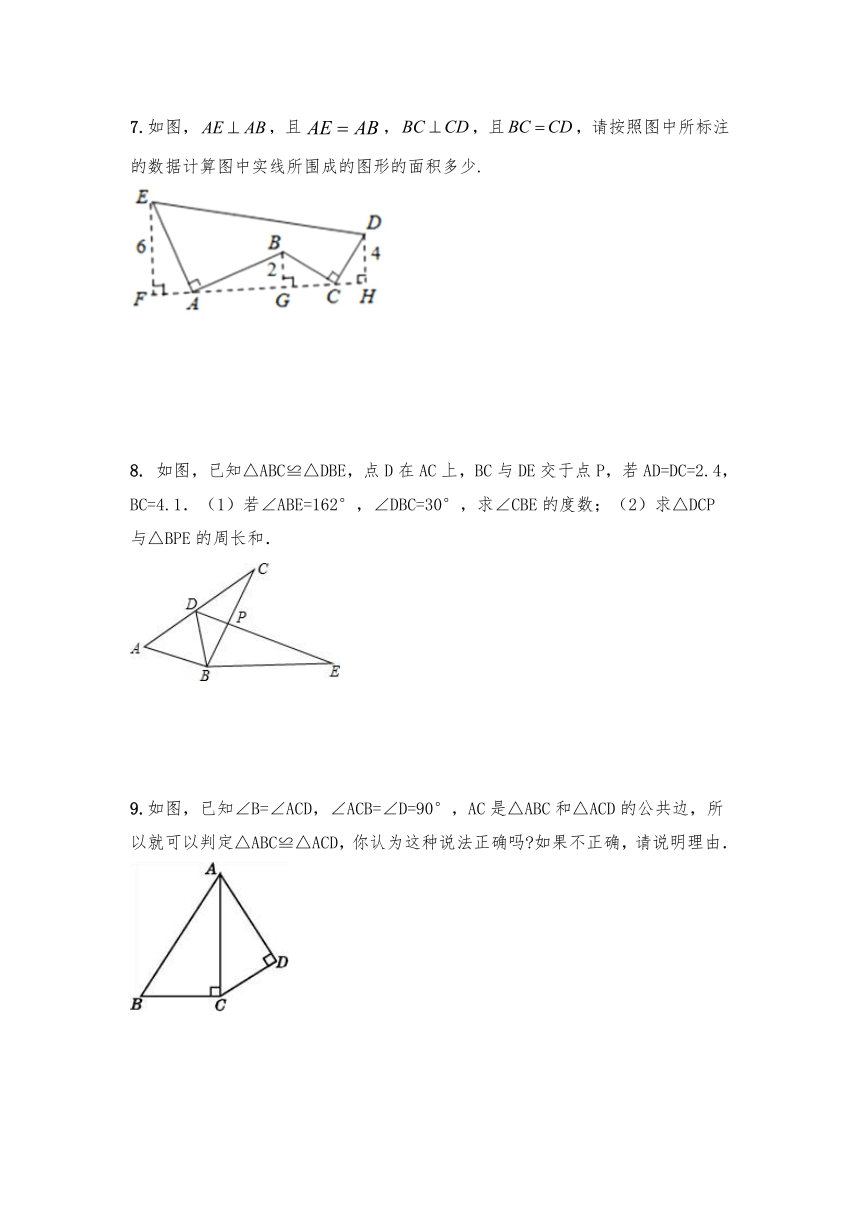
5.如图,点在直线的同侧,过作,垂足为,延长至,使得,连接交直线于点.(1)求证:(2)在直线上任意一点(除点外),求证:
6.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,求∠BDC的度数.
7.如图,,且,,且,请按照图中所标注的数据计算图中实线所围成的图形的面积多少.
8.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;(2)求△DCP与△BPE的周长和.
9.如图,已知∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD,你认为这种说法正确吗?如果不正确,请说明理由.
10.如图,在中,,,点是内部一点,且,证明:.
11.如图,ABC中,∠ACB=90°,AC=6cm,BC=8cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2cm/s和3cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t秒,则当t=_____秒时,PEC与QFC全等.
12.如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为_____.
13.如图
1,点
P、Q
分别是等边△ABC
边
AB、BC
上的动点(端点除外),点
P
从顶点
A、点
Q
从顶点
B
同时出发,且它们的运动速度相同,连接AQ、CP
交于点
M.
(1)求证:△ABQ≌△CAP;(2)当点
P、Q
分别在
AB、BC
边上运动时,∠QMC
变化吗?若变化,请说明理由;若不变,求出它的度数.(3)如图
2,若点
P、Q在运动到终点后继续在射线AB、BC上运动,直线
AQ、CP交点为M,则∠QMC
变化吗?若变化,请说明理由;若不变,则求出它的度数.
14.如图(1),在ABC中,,BC=9cm,
AC=12cm,
AB=15cm.现有一动点P,从点A出发,沿着三角形的边ACCBBA运动,回到点A停止,速度为3cm/s,设运动时间为t
s.(1)如图(1),当t=______时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,,DE=4cm,
DF=5cm,
.
在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着ABBCCA运动,回到点A停止.在两点运动过程中的某一时刻,恰好,求点Q的运动速度.
15.如图所示,△ABC中,∠ACB=90°,AC=6cm,BC
=8cm.点P从A点出发,沿路径向终点B运动,点Q从B点出发,沿路径向终点A运动.点P
和Q分别和的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
16.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,以D为顶点作,交边AC,BC于点M,N.(1)如图(1),若,,当绕点D旋转时,AM,MN,BN三条线段之间有何种数量关系?证明你的结论;(2)如图(2),当时,AM,MN,BN三条线段之间有何数量关系?证明你的结论;(3)如图(3),在(2)的条件下,若将M,N分别改在CA,BC的延长线上,完成图(3),其余条件不变,则AM,MN,BN之间有何数量关系(直接写出结论,不必证明).
17.(1)如图1,在ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,把AB,AC,2AD集中在ACE中,利用三角形三边关系可得AD的取值范围是
;(2)如图2,在ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF>EF;(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F分别在BC,AB上,且∠EDF=∠ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.
18.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在中,,若点D为AB的中点,则.
请结合上述结论解决如下问题:已知,点P是射线BA上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB的中点(1)如图2,当点P与点Q重合时,AE与BF的位置关系____________;QE与QF的数量关系是__________(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
答案
一、解答题
1.(1)∵∠DCE=∠A,∴∠D+∠ACD=∠ACD+∠BCE,∴∠D=∠BCE,
在△ACD和△BEC中,,∴△ACD≌△BEC(AAS);
(2)∵△ACD≌△BEC,∴AD=BC,AC=BE,∴AC+BC=AD+BE,即AB=AD+BE.
2.证明:
在△ABC和△DEC中,,
(2)∵∠ACD=90°,AC=CD,∴∠1=∠D=45°,
∵AE=AC,∴∠3=∠5=67.5°,∴∠DEC=180°-∠5=112.5°.
3.(1)∵△ABC与△DEF是互补三角形,∴∠ACB+∠E=180°,AC=DE,BC=EF.
又∵∠ACB+∠ACG=180°,∴∠ACG=∠E,
在△AGC与△DHE中,∴△AGC≌△DHE(AAS)
∴AG=DH.∴,即△ABC与△DEF的面积相等.
(2)不正确.反例如解图,在△ABC和△DEF中,∴△ABC≌△DEF(SAS),
∴△ABC与△DEF是互补三角形.∴互补三角形一定不全等的说法错误.
4.证明:(1)∵BE⊥CD,∴∠BEC=∠DEA=90°,
在Rt△BEC与Rt△DEA中,∵,∴△BEC≌△DEA(HL);
(2)∵由(1)知,△BEC≌△DEA,∴∠B=∠D.
∵∠D+∠DAE=90°,∠DAE=∠BAF,∴∠BAF+∠B=90°,即DF⊥BC.
5.(1),
在和中
(2)在上取一点,连接,,
在中,
6.解:延长AE交DC边于点F,如图:
∵∠ABC=90°,∴∠CBD=90°,在Rt△ABE与Rt△CBD中,
∴Rt△ABE≌Rt△CBD(HL),∴∠AEB=∠BDC,AB=BC,∴∠BAC=∠ACB=45°,
∵∠AEB为△AEC的外角,∠CAE=30°,∴∠AEB=∠ACB+∠CAE=45°+30°=75°,
∴∠BDC=75°.故答案为:75°.
7.∵AE⊥AB,EF⊥AF,BG⊥AG,∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,∴∠FEA=∠BAG,
在△FEA和△GAB中,,∴△FEA≌△GAB(AAS),∴AG=EF=6,AF=BG=2,
同理可证:△CBG≌△DCH(AAS),∴CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,∴梯形EFHD的面积=×(EF+DH)×FH=×(6+4)×14=70,
∴阴影部分的面积=S梯形EFHD?S△EFA?S△ABC?S△DHC=70?×6×2?×(6+4)×2?×4×2=50.故答案为50.
8.解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,∴∠ABC=∠DBE,∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4.
9.解:不正确,因为AC不是△ABC和△ACD的对应边,故不能判定△ABC≌△ACD.
10.证明:如图,在线段上取点,使得,连接,
,,,,
在中,,,,
,,,
在和中,,
,,是等腰直角三角形,,
,.
11.解:由题意得,AP=2t,BQ=3t,∵AC=6cm,BC=8cm,∴CP=6﹣2t,CQ=8﹣3t,
①如图1,当△PEC≌△CFQ时,则PC=CQ,即6﹣2t=8﹣3t,解得:t=2,
②如图2,当点Q与P重合时,△PEC≌△QFC全等,
则PC=CQ,∴6﹣2t=3t﹣8.解得:t=,
③如图3,当点Q与A重合时,△PEC≌△CFQ,
则PC=CQ,即2t-6=6,解得:t=6,
综上所述:当t=2秒或秒或6秒时,△PEC与△QFC全等,
故答案为:2或或6.
12.当△ACP≌△BPQ,∴AP=BQ,∵运动时间相同,∴P,Q的运动速度也相同,∴x=2.
当△ACP≌△BQP时,AC=BQ=4,PA=PB,∴t=1.5,∴x==
故答案为2或.
13.(1)证明:∵△ABC是等边三角形∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,∵,∴△ABQ≌△CAP(SAS);
(2)解:点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)解:点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°?∠PAC=180°?60°=120°.
14.(1)
∵△APC的面积等于△ABC面积的一半
当P点运动到BC边上时,此时
即
此时
当P点运动到AB边上时,作PQ⊥AC于Q
此时即
∴此时P点在AB边的中点,此时
综上所述,当t=或时,△APC的面积等于△ABC面积的一半
(2)∵,DE=4cm,
DF=5cm,
此时P点运动的时间为
∵P,Q同时出发,所以Q运动的时间也是∴Q运动的速度为
15.设运动时间为秒时,和全等,
∵和全等,∴,
有三种情况:如图1所示,在上,在上,,,∴,∴.
(2)如图2所示,,都在上,此时,重合,,,∴,∴.
(3)如图3所示,当到达点(和点重合),在上时,此时点停止运动,
∵,,,∴,∴.∵,∴符合题意.
答:点运动1秒或3.5秒或12秒时,和全等.
16.(1).证明如下:如图,延长CB到E,使,连接DE.
,.,.
在和中,,,,.
,,,.
在和中,,,.
,;
(2).证明如下:如图,延长CB到E,使,连接DE.
,.,,.
在和中,,,,.
,,,,
,,.
在和中,,,.
,;
(3)补充完成题图,如图所示.
.证明如下:如上图,在CB上截取BE=AM,连接DE.
,,,.
,.
在和中,,,
,.
,,.
在和中,,,.
,.
17.(1)∵CD=BD,AD=DE,∠CDE=∠ADB,∴△CDE≌△BDA(SAS),∴EC=AB=4,
∵6﹣4<AE<6+4,∴2<2AD<10,∴1<AD<5,故答案为:1<AD<5;
(2)如图2中,延长ED到H,使得DH=DE,连接DH,FH.
∵BD=DC,∠BDE=∠CDH,DE=DH,∴△BDE≌△CDH(SAS),∴BE=CH,
∵FD⊥EH,又DE=DH,∴EF=FH,在△CFH中,CH+CF>FH,
∵CH=BE,FH=EF,∴BE+CF>EF;
(3)结论:AF+EC=EF.理由:延长BC到H,使得CH=AF.
∵∠B+∠ADC=180°,∴∠A+∠BCD=180°,∵∠DCH+∠BCD=180°,∴A=∠DCH,
∵AF=CH,AD=CD,∴△AFD≌△CHD(SAS),∴DF=DH,∠ADF=∠CDH,∴∠ADC=∠FDH,
∵∠EDF=∠ADC,∴∠EDF=∠FDH,∴∠EDF=∠EDH,
∵DE=DE,∴△EDF≌△EDH(SAS),∴EF=EH,
∵EH=EC+CH=EC+AF,∴EF=AF+EC.
18.(1)AE//BF;QE=QF
(2)QE=QF
证明:延长EQ交BF于D,
,
(3)当点P在线段BA延长线上时,此时(2)中结论成立
证明:延长EQ交FB的延长于D
因为AE//BF所以
EQ=QF
一、解答题
1.如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.
(1)说明△ACD与△BEC全等的理由;(2)说明AB=AD+BE的理由.
2.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,
∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.
3.综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
……
(将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.
4.已知:BE⊥CD于E,BE=DE,BC=DA,(1)求证:△BEC≌△DEA;(2)求证:BC⊥FD.
5.如图,点在直线的同侧,过作,垂足为,延长至,使得,连接交直线于点.(1)求证:(2)在直线上任意一点(除点外),求证:
6.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,求∠BDC的度数.
7.如图,,且,,且,请按照图中所标注的数据计算图中实线所围成的图形的面积多少.
8.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;(2)求△DCP与△BPE的周长和.
9.如图,已知∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD,你认为这种说法正确吗?如果不正确,请说明理由.
10.如图,在中,,,点是内部一点,且,证明:.
11.如图,ABC中,∠ACB=90°,AC=6cm,BC=8cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2cm/s和3cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t秒,则当t=_____秒时,PEC与QFC全等.
12.如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为_____.
13.如图
1,点
P、Q
分别是等边△ABC
边
AB、BC
上的动点(端点除外),点
P
从顶点
A、点
Q
从顶点
B
同时出发,且它们的运动速度相同,连接AQ、CP
交于点
M.
(1)求证:△ABQ≌△CAP;(2)当点
P、Q
分别在
AB、BC
边上运动时,∠QMC
变化吗?若变化,请说明理由;若不变,求出它的度数.(3)如图
2,若点
P、Q在运动到终点后继续在射线AB、BC上运动,直线
AQ、CP交点为M,则∠QMC
变化吗?若变化,请说明理由;若不变,则求出它的度数.
14.如图(1),在ABC中,,BC=9cm,
AC=12cm,
AB=15cm.现有一动点P,从点A出发,沿着三角形的边ACCBBA运动,回到点A停止,速度为3cm/s,设运动时间为t
s.(1)如图(1),当t=______时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,,DE=4cm,
DF=5cm,
.
在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着ABBCCA运动,回到点A停止.在两点运动过程中的某一时刻,恰好,求点Q的运动速度.
15.如图所示,△ABC中,∠ACB=90°,AC=6cm,BC
=8cm.点P从A点出发,沿路径向终点B运动,点Q从B点出发,沿路径向终点A运动.点P
和Q分别和的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
16.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,以D为顶点作,交边AC,BC于点M,N.(1)如图(1),若,,当绕点D旋转时,AM,MN,BN三条线段之间有何种数量关系?证明你的结论;(2)如图(2),当时,AM,MN,BN三条线段之间有何数量关系?证明你的结论;(3)如图(3),在(2)的条件下,若将M,N分别改在CA,BC的延长线上,完成图(3),其余条件不变,则AM,MN,BN之间有何数量关系(直接写出结论,不必证明).
17.(1)如图1,在ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,把AB,AC,2AD集中在ACE中,利用三角形三边关系可得AD的取值范围是
;(2)如图2,在ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF>EF;(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F分别在BC,AB上,且∠EDF=∠ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.
18.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在中,,若点D为AB的中点,则.
请结合上述结论解决如下问题:已知,点P是射线BA上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB的中点(1)如图2,当点P与点Q重合时,AE与BF的位置关系____________;QE与QF的数量关系是__________(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
答案
一、解答题
1.(1)∵∠DCE=∠A,∴∠D+∠ACD=∠ACD+∠BCE,∴∠D=∠BCE,
在△ACD和△BEC中,,∴△ACD≌△BEC(AAS);
(2)∵△ACD≌△BEC,∴AD=BC,AC=BE,∴AC+BC=AD+BE,即AB=AD+BE.
2.证明:
在△ABC和△DEC中,,
(2)∵∠ACD=90°,AC=CD,∴∠1=∠D=45°,
∵AE=AC,∴∠3=∠5=67.5°,∴∠DEC=180°-∠5=112.5°.
3.(1)∵△ABC与△DEF是互补三角形,∴∠ACB+∠E=180°,AC=DE,BC=EF.
又∵∠ACB+∠ACG=180°,∴∠ACG=∠E,
在△AGC与△DHE中,∴△AGC≌△DHE(AAS)
∴AG=DH.∴,即△ABC与△DEF的面积相等.
(2)不正确.反例如解图,在△ABC和△DEF中,∴△ABC≌△DEF(SAS),
∴△ABC与△DEF是互补三角形.∴互补三角形一定不全等的说法错误.
4.证明:(1)∵BE⊥CD,∴∠BEC=∠DEA=90°,
在Rt△BEC与Rt△DEA中,∵,∴△BEC≌△DEA(HL);
(2)∵由(1)知,△BEC≌△DEA,∴∠B=∠D.
∵∠D+∠DAE=90°,∠DAE=∠BAF,∴∠BAF+∠B=90°,即DF⊥BC.
5.(1),
在和中
(2)在上取一点,连接,,
在中,
6.解:延长AE交DC边于点F,如图:
∵∠ABC=90°,∴∠CBD=90°,在Rt△ABE与Rt△CBD中,
∴Rt△ABE≌Rt△CBD(HL),∴∠AEB=∠BDC,AB=BC,∴∠BAC=∠ACB=45°,
∵∠AEB为△AEC的外角,∠CAE=30°,∴∠AEB=∠ACB+∠CAE=45°+30°=75°,
∴∠BDC=75°.故答案为:75°.
7.∵AE⊥AB,EF⊥AF,BG⊥AG,∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,∴∠FEA=∠BAG,
在△FEA和△GAB中,,∴△FEA≌△GAB(AAS),∴AG=EF=6,AF=BG=2,
同理可证:△CBG≌△DCH(AAS),∴CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,∴梯形EFHD的面积=×(EF+DH)×FH=×(6+4)×14=70,
∴阴影部分的面积=S梯形EFHD?S△EFA?S△ABC?S△DHC=70?×6×2?×(6+4)×2?×4×2=50.故答案为50.
8.解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,∴∠ABC=∠DBE,∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4.
9.解:不正确,因为AC不是△ABC和△ACD的对应边,故不能判定△ABC≌△ACD.
10.证明:如图,在线段上取点,使得,连接,
,,,,
在中,,,,
,,,
在和中,,
,,是等腰直角三角形,,
,.
11.解:由题意得,AP=2t,BQ=3t,∵AC=6cm,BC=8cm,∴CP=6﹣2t,CQ=8﹣3t,
①如图1,当△PEC≌△CFQ时,则PC=CQ,即6﹣2t=8﹣3t,解得:t=2,
②如图2,当点Q与P重合时,△PEC≌△QFC全等,
则PC=CQ,∴6﹣2t=3t﹣8.解得:t=,
③如图3,当点Q与A重合时,△PEC≌△CFQ,
则PC=CQ,即2t-6=6,解得:t=6,
综上所述:当t=2秒或秒或6秒时,△PEC与△QFC全等,
故答案为:2或或6.
12.当△ACP≌△BPQ,∴AP=BQ,∵运动时间相同,∴P,Q的运动速度也相同,∴x=2.
当△ACP≌△BQP时,AC=BQ=4,PA=PB,∴t=1.5,∴x==
故答案为2或.
13.(1)证明:∵△ABC是等边三角形∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,∵,∴△ABQ≌△CAP(SAS);
(2)解:点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)解:点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°?∠PAC=180°?60°=120°.
14.(1)
∵△APC的面积等于△ABC面积的一半
当P点运动到BC边上时,此时
即
此时
当P点运动到AB边上时,作PQ⊥AC于Q
此时即
∴此时P点在AB边的中点,此时
综上所述,当t=或时,△APC的面积等于△ABC面积的一半
(2)∵,DE=4cm,
DF=5cm,
此时P点运动的时间为
∵P,Q同时出发,所以Q运动的时间也是∴Q运动的速度为
15.设运动时间为秒时,和全等,
∵和全等,∴,
有三种情况:如图1所示,在上,在上,,,∴,∴.
(2)如图2所示,,都在上,此时,重合,,,∴,∴.
(3)如图3所示,当到达点(和点重合),在上时,此时点停止运动,
∵,,,∴,∴.∵,∴符合题意.
答:点运动1秒或3.5秒或12秒时,和全等.
16.(1).证明如下:如图,延长CB到E,使,连接DE.
,.,.
在和中,,,,.
,,,.
在和中,,,.
,;
(2).证明如下:如图,延长CB到E,使,连接DE.
,.,,.
在和中,,,,.
,,,,
,,.
在和中,,,.
,;
(3)补充完成题图,如图所示.
.证明如下:如上图,在CB上截取BE=AM,连接DE.
,,,.
,.
在和中,,,
,.
,,.
在和中,,,.
,.
17.(1)∵CD=BD,AD=DE,∠CDE=∠ADB,∴△CDE≌△BDA(SAS),∴EC=AB=4,
∵6﹣4<AE<6+4,∴2<2AD<10,∴1<AD<5,故答案为:1<AD<5;
(2)如图2中,延长ED到H,使得DH=DE,连接DH,FH.
∵BD=DC,∠BDE=∠CDH,DE=DH,∴△BDE≌△CDH(SAS),∴BE=CH,
∵FD⊥EH,又DE=DH,∴EF=FH,在△CFH中,CH+CF>FH,
∵CH=BE,FH=EF,∴BE+CF>EF;
(3)结论:AF+EC=EF.理由:延长BC到H,使得CH=AF.
∵∠B+∠ADC=180°,∴∠A+∠BCD=180°,∵∠DCH+∠BCD=180°,∴A=∠DCH,
∵AF=CH,AD=CD,∴△AFD≌△CHD(SAS),∴DF=DH,∠ADF=∠CDH,∴∠ADC=∠FDH,
∵∠EDF=∠ADC,∴∠EDF=∠FDH,∴∠EDF=∠EDH,
∵DE=DE,∴△EDF≌△EDH(SAS),∴EF=EH,
∵EH=EC+CH=EC+AF,∴EF=AF+EC.
18.(1)AE//BF;QE=QF
(2)QE=QF
证明:延长EQ交BF于D,
,
(3)当点P在线段BA延长线上时,此时(2)中结论成立
证明:延长EQ交FB的延长于D
因为AE//BF所以
EQ=QF
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
