北师大版七年级数学下册1.4整式的乘法一课一练习题1(Word版,含答案)
文档属性
| 名称 | 北师大版七年级数学下册1.4整式的乘法一课一练习题1(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 357.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览




文档简介
1.4《整式的乘法》习题1
一、选择题
1.如果,那么p、q的值是(
)
A.p=5,
q=6
B.p=-1,
q=-6
C.p=1,
q=-6
D.p=-5,
q=-6
2.(﹣3x+1)(﹣2x)2等于( )
A.﹣6x3﹣2x2
B.6x3﹣2x2
C.6x3+2x2
D.﹣12x3+4x2
3.若单项式和的积为,则的值为(
)
A.2
B.30
C.-15
D.15
4.一个三角形的底边为2m,高为m+4n,它的面积为(
)
A.m2+4mn
B.2m2+8mn
C.m2+8mn
D.
5.在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:﹣3x(﹣2x2+3x﹣1)=6x3﹣9x2+□,“□”的地方被墨水弄污了,你认为“□”内应填写(
)
A.1
B.﹣1
C.3x
D.﹣3x
6.图为“”型钢材的截面,要计算其截面面积,下列给出的算式中,错误的是( )
A.
B.
C.
D.
7.若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为(
)
A.6,3,1
B.3,6,1
C.2,1,3
D.2,3,1
8.若,,则代数式的值等于(
)
A.
B.
C.
D.
9.展开后不含和的项,则、的值为(
)
A.
B.
C.
D.
10.定义运算:?b=(1-b).下面给出了关于这种运算的几种结论:①2?(-2)=6;②?b=b?;③若+b=0,则(?)+(b?b)=2b;④若?b=0,则=0或b=1;其中结论正确的序号是(
)
A.①④
B.①③
C.②③④
D.①③④
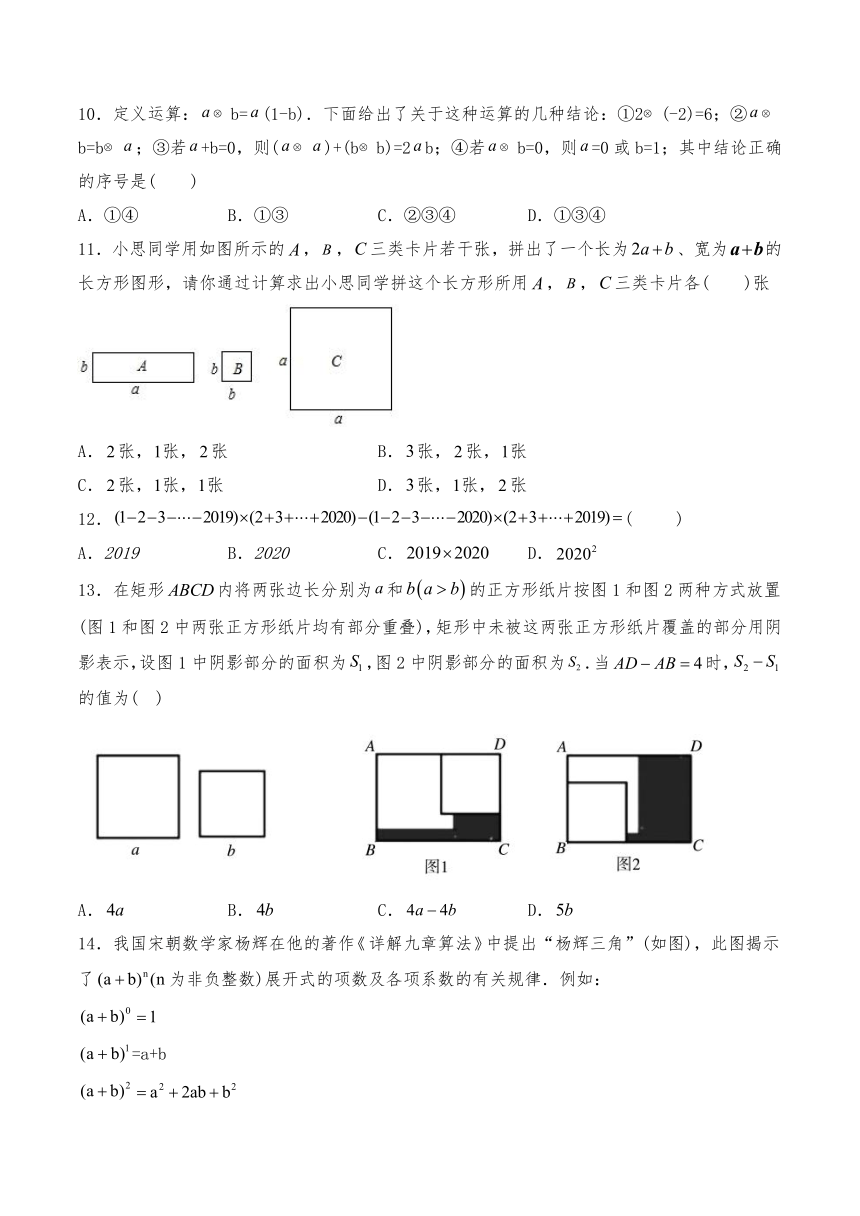
11.小思同学用如图所示的,,三类卡片若干张,拼出了一个长为、宽为的长方形图形,请你通过计算求出小思同学拼这个长方形所用,,三类卡片各(
)张
A.张,张,张
B.张,张,张
C.张,张,张
D.张,张,张
12.(
)
A.2019
B.2020
C.
D.
13.在矩形内将两张边长分别为和的正方形纸片按图1和图2两种方式放置(图1和图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为.当时,的值为(
)
A.
B.
C.
D.
14.我国宋朝数学家杨辉在他的著作详解九章算法中提出“杨辉三角”(如图),此图揭示了为非负整数)展开式的项数及各项系数的有关规律.例如:
=a+b
……
请你猜想的展开式中所有系数的和是(
)
A.
B.
C.
D.
二、填空题
15.下图中的四边形均为长方形,根据图形面积,写出一个正确的等式:______.
16.若,则的值为______.
17.数学家发明了一个魔术盒,当任意有理数对进入其中时,会得到一个新的有理数,现将数对放入其中的得到数再将数对放入其中,最后得到的数是_____________.(结果要化简)
18.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第6个图形需要黑色棋子的个数是______,第个图形需要的黑色棋子的个数是______.(为正整数)
三、解答题
19.先化简,再求值:,其中.
20.已知x、y为有理数,现规定一种新运算,满足.
(1)求的值;
(2)求的值;
(3)探索与的关系,并用等式把它们表达出来.
21.在日历上,我们可以发现其中某些数满足一定的规律,如下图是2021年1月份的日历,我们任意用一个的方框框出4个数,将其中4个位置上的数两两交叉相乘,再用较大的数减去较小的数,你发现了什么规律?
(1)图中方框框出的四个数,按照题目所说的计算规律,结果为______.
(2)换一个位置试一下,是否有同样的规律?如果有,请你利用整式的运算对你发现的规律加以证明;如果没有,请说明理由.
22.长方形的长为厘米,宽为厘米,其中,如果将原长方形的长和宽各增加3厘米,得到的新长方形面积记为,如果将原长方形的长和宽分别减少2厘米,得到的新长方形面积记为.
(1)若、为正整数,请说明:与的差一定是5的倍数;
(2)如果,求将原长方形的长和宽分别减少7厘米后得到的新长方形面积.
23.小刚同学计算一道整式乘法:,由于他抄错了多项式中前面的符号,把“+”写成“一”,得到的结果为.
(1)求、的值.
(2)计算这道整式乘法的正确结果.
24.仔细观察,探索规律:
(1)(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4.
(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)=①
(其中n为正整数,且n≥2).
②(2﹣1)(2+1)=
;③(2﹣1)(22+2+1)=
;
④(2﹣1)(23+22+2+1)=
;⑤(2n﹣1+2n﹣2+…+2+1)=
;
(2)根据上述规律,求22019+22018+22017+…+2+1的个位数字是多少?
(3)根据上述规律,求29﹣28+27﹣…+23﹣22+2的值?
25.准备若干张如图一所示边长为?的正方形和边长分别为?的长方形卡片,用这些卡片拼出新的图形,用不同的方法计算它的面积,可以得到一些等式.请解答下列问题:
(1)由图二,可得等式______.
(2)圆圆同学用x张边长为a的正方形?y张边长为b的正方形和z张边长分别为a?b的长方形纸片,拼出一个面积为长方形,求的值.
(3)已知这两个边长为a?b的正方形面积和为60,边长为a?b的长方形面积为20.点点同学将这两个正方形拼成图三形状,B?C?G三点在同一直线上,连接和.求阴影部分的面积.
26.好学的晓璐同学,在学习多项式乘以多项式时发现:(x+4)(2x+5)(3x﹣6)的结果是一个多项式,并且最高次项为:x?2x?3x=3x3,常数项为:4×5×(﹣6)=﹣120,那么一次项是多少呢?
根据尝试和总结她发现:一次项就是:x×5×(﹣6)+2x×4×(﹣6)+3x×4×5=﹣3x.
请你认真领会晓璐同学解决问题的思路、方法,仔细分析上面等式的结构特征,结合自己对多项式乘法法则的理解,解决以下问题:
(1)计算(x+2)(3x+1)(5x﹣3)所得多项式的最高次项为
,一次项为
;
(2)若计算(x+1)(﹣3x+m)(2x﹣1)(m为常数)所得的多项式不含一次项,求m的值;
(3)若(x+1)2021=a0x2021+a1x2020+a2x2019+…+a2020x+a2021,则a2020=
.
答案
一、选择题
1.C.2.D.3.D.4.A.5.C.6.A.7.B.8.A.9.A.
10.D.11.D.12.B.13.B.14.C.
二、填空题
15.
16.15
17.
18.48
三、解答题
19.原式
,
当时,
原式.
20.解:(1)∵,
∴;
(2),
∴;
(3))∵,
∴
∴=+1.
21.(1)11×5-4×12=55-48=7,
故答案为:7;
(2)换为3,4,10,11,则10×4-3×11=40-33=7;
设方框框出的四个数分别为a,a+1,a+7,a+8,
则(a+1)(a+7)-a(a+8)
=a2+7a+a+7-a2-8a
=7.
22.
(1)证明:由题意得:S1=(a+3)(b+3)=ab+3(a+b)+9
S2=(a-2)(b-2)=ab-2(a+b)+4
S1-S2=[ab+3(a+b)+9]-[ab-2(a+b)+4]
=ab+3(a+b)+9-ab+2(a+b)-4
=5(a+b)+5
=5(a+b+1)
∴S1与S2的差一定是5的倍数.
(2)∵S1=2S2
∴ab+3(a+b)+9=2[ab-2(a+b)+4]
∴ab-7a-7b-1=0
∴ab-7a-7b=1
∴将原长方形的长和宽分别减少7厘米后得到的新长方形面积为:(a-7)(b-7)=ab-7a-7b+49=1+49=50.
∴将原长方形的长和宽分别减少7厘米后得到的新长方形面积为50平方厘米.
23.解:(1)由题意,得
,.
(2).
24.解:(1)①由上式的规律可得,an﹣bn,
故答案为:an﹣bn;
由题干中提供的等式的规律可得,
②(2+1)(2﹣1)=22﹣1;
③(2﹣1)(22+2+1)=23﹣1;
④(2﹣1)(23+22+2+1)=24﹣1;
⑤(2n﹣1+2n﹣2+…+2+1)=(2﹣1)(2n﹣1+2n﹣2+…+2+1)=2n﹣1;
(2)22019+22018+22017+…+2+1
=(2﹣1)(22019+22018+22017+…+2+1)
=22020﹣1,
又∵21=2,22=4,23=8,24=16,25=32,……
∴22020的个位数字为6,
∴22020﹣1的个位数字为6﹣1=5,
答:22019+22018+22017+…+2+1的个位数字是5.
(3)29﹣28+27﹣…+23﹣22+2
=28(2﹣1)+26(2﹣1)+24(2﹣1)+22(2﹣1)+2
=28+26+24+22+2
=256+64+16+4+2
=342.
25.(1)由图可知,大长方形的面积等于三个正方形的面积与三个长方形的面积之和,
则,
故答案为:;
(2)由题意得:,
,
∴,
则;
(3)由题意得:,
则,
,
,
,
,
,
即阴影部分的面积为20.
26.(1)由题意得:
(x+2)(3x+1)(5x﹣3)所得多项式的最高次项为x×3x×5x=15x3,
一次项为:1×1×(﹣3)x+2×3×(﹣3)x+2×1×5x=﹣11x,
故答案为:15x3,﹣11x;
(2)依题意有:1×m×(﹣1)+1×(﹣3)×(﹣1)+1×m×2=0,
解得m=﹣3;
(3)根据题意可知即为所得多项式的一次项系数,
∵展开之后x的一次项共有2021个,且每一项的系数都为,
∴
故答案为:2021.
一、选择题
1.如果,那么p、q的值是(
)
A.p=5,
q=6
B.p=-1,
q=-6
C.p=1,
q=-6
D.p=-5,
q=-6
2.(﹣3x+1)(﹣2x)2等于( )
A.﹣6x3﹣2x2
B.6x3﹣2x2
C.6x3+2x2
D.﹣12x3+4x2
3.若单项式和的积为,则的值为(
)
A.2
B.30
C.-15
D.15
4.一个三角形的底边为2m,高为m+4n,它的面积为(
)
A.m2+4mn
B.2m2+8mn
C.m2+8mn
D.
5.在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:﹣3x(﹣2x2+3x﹣1)=6x3﹣9x2+□,“□”的地方被墨水弄污了,你认为“□”内应填写(
)
A.1
B.﹣1
C.3x
D.﹣3x
6.图为“”型钢材的截面,要计算其截面面积,下列给出的算式中,错误的是( )
A.
B.
C.
D.
7.若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为(
)
A.6,3,1
B.3,6,1
C.2,1,3
D.2,3,1
8.若,,则代数式的值等于(
)
A.
B.
C.
D.
9.展开后不含和的项,则、的值为(
)
A.
B.
C.
D.
10.定义运算:?b=(1-b).下面给出了关于这种运算的几种结论:①2?(-2)=6;②?b=b?;③若+b=0,则(?)+(b?b)=2b;④若?b=0,则=0或b=1;其中结论正确的序号是(
)
A.①④
B.①③
C.②③④
D.①③④
11.小思同学用如图所示的,,三类卡片若干张,拼出了一个长为、宽为的长方形图形,请你通过计算求出小思同学拼这个长方形所用,,三类卡片各(
)张
A.张,张,张
B.张,张,张
C.张,张,张
D.张,张,张
12.(
)
A.2019
B.2020
C.
D.
13.在矩形内将两张边长分别为和的正方形纸片按图1和图2两种方式放置(图1和图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为.当时,的值为(
)
A.
B.
C.
D.
14.我国宋朝数学家杨辉在他的著作详解九章算法中提出“杨辉三角”(如图),此图揭示了为非负整数)展开式的项数及各项系数的有关规律.例如:
=a+b
……
请你猜想的展开式中所有系数的和是(
)
A.
B.
C.
D.
二、填空题
15.下图中的四边形均为长方形,根据图形面积,写出一个正确的等式:______.
16.若,则的值为______.
17.数学家发明了一个魔术盒,当任意有理数对进入其中时,会得到一个新的有理数,现将数对放入其中的得到数再将数对放入其中,最后得到的数是_____________.(结果要化简)
18.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第6个图形需要黑色棋子的个数是______,第个图形需要的黑色棋子的个数是______.(为正整数)
三、解答题
19.先化简,再求值:,其中.
20.已知x、y为有理数,现规定一种新运算,满足.
(1)求的值;
(2)求的值;
(3)探索与的关系,并用等式把它们表达出来.
21.在日历上,我们可以发现其中某些数满足一定的规律,如下图是2021年1月份的日历,我们任意用一个的方框框出4个数,将其中4个位置上的数两两交叉相乘,再用较大的数减去较小的数,你发现了什么规律?
(1)图中方框框出的四个数,按照题目所说的计算规律,结果为______.
(2)换一个位置试一下,是否有同样的规律?如果有,请你利用整式的运算对你发现的规律加以证明;如果没有,请说明理由.
22.长方形的长为厘米,宽为厘米,其中,如果将原长方形的长和宽各增加3厘米,得到的新长方形面积记为,如果将原长方形的长和宽分别减少2厘米,得到的新长方形面积记为.
(1)若、为正整数,请说明:与的差一定是5的倍数;
(2)如果,求将原长方形的长和宽分别减少7厘米后得到的新长方形面积.
23.小刚同学计算一道整式乘法:,由于他抄错了多项式中前面的符号,把“+”写成“一”,得到的结果为.
(1)求、的值.
(2)计算这道整式乘法的正确结果.
24.仔细观察,探索规律:
(1)(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4.
(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)=①
(其中n为正整数,且n≥2).
②(2﹣1)(2+1)=
;③(2﹣1)(22+2+1)=
;
④(2﹣1)(23+22+2+1)=
;⑤(2n﹣1+2n﹣2+…+2+1)=
;
(2)根据上述规律,求22019+22018+22017+…+2+1的个位数字是多少?
(3)根据上述规律,求29﹣28+27﹣…+23﹣22+2的值?
25.准备若干张如图一所示边长为?的正方形和边长分别为?的长方形卡片,用这些卡片拼出新的图形,用不同的方法计算它的面积,可以得到一些等式.请解答下列问题:
(1)由图二,可得等式______.
(2)圆圆同学用x张边长为a的正方形?y张边长为b的正方形和z张边长分别为a?b的长方形纸片,拼出一个面积为长方形,求的值.
(3)已知这两个边长为a?b的正方形面积和为60,边长为a?b的长方形面积为20.点点同学将这两个正方形拼成图三形状,B?C?G三点在同一直线上,连接和.求阴影部分的面积.
26.好学的晓璐同学,在学习多项式乘以多项式时发现:(x+4)(2x+5)(3x﹣6)的结果是一个多项式,并且最高次项为:x?2x?3x=3x3,常数项为:4×5×(﹣6)=﹣120,那么一次项是多少呢?
根据尝试和总结她发现:一次项就是:x×5×(﹣6)+2x×4×(﹣6)+3x×4×5=﹣3x.
请你认真领会晓璐同学解决问题的思路、方法,仔细分析上面等式的结构特征,结合自己对多项式乘法法则的理解,解决以下问题:
(1)计算(x+2)(3x+1)(5x﹣3)所得多项式的最高次项为
,一次项为
;
(2)若计算(x+1)(﹣3x+m)(2x﹣1)(m为常数)所得的多项式不含一次项,求m的值;
(3)若(x+1)2021=a0x2021+a1x2020+a2x2019+…+a2020x+a2021,则a2020=
.
答案
一、选择题
1.C.2.D.3.D.4.A.5.C.6.A.7.B.8.A.9.A.
10.D.11.D.12.B.13.B.14.C.
二、填空题
15.
16.15
17.
18.48
三、解答题
19.原式
,
当时,
原式.
20.解:(1)∵,
∴;
(2),
∴;
(3))∵,
∴
∴=+1.
21.(1)11×5-4×12=55-48=7,
故答案为:7;
(2)换为3,4,10,11,则10×4-3×11=40-33=7;
设方框框出的四个数分别为a,a+1,a+7,a+8,
则(a+1)(a+7)-a(a+8)
=a2+7a+a+7-a2-8a
=7.
22.
(1)证明:由题意得:S1=(a+3)(b+3)=ab+3(a+b)+9
S2=(a-2)(b-2)=ab-2(a+b)+4
S1-S2=[ab+3(a+b)+9]-[ab-2(a+b)+4]
=ab+3(a+b)+9-ab+2(a+b)-4
=5(a+b)+5
=5(a+b+1)
∴S1与S2的差一定是5的倍数.
(2)∵S1=2S2
∴ab+3(a+b)+9=2[ab-2(a+b)+4]
∴ab-7a-7b-1=0
∴ab-7a-7b=1
∴将原长方形的长和宽分别减少7厘米后得到的新长方形面积为:(a-7)(b-7)=ab-7a-7b+49=1+49=50.
∴将原长方形的长和宽分别减少7厘米后得到的新长方形面积为50平方厘米.
23.解:(1)由题意,得
,.
(2).
24.解:(1)①由上式的规律可得,an﹣bn,
故答案为:an﹣bn;
由题干中提供的等式的规律可得,
②(2+1)(2﹣1)=22﹣1;
③(2﹣1)(22+2+1)=23﹣1;
④(2﹣1)(23+22+2+1)=24﹣1;
⑤(2n﹣1+2n﹣2+…+2+1)=(2﹣1)(2n﹣1+2n﹣2+…+2+1)=2n﹣1;
(2)22019+22018+22017+…+2+1
=(2﹣1)(22019+22018+22017+…+2+1)
=22020﹣1,
又∵21=2,22=4,23=8,24=16,25=32,……
∴22020的个位数字为6,
∴22020﹣1的个位数字为6﹣1=5,
答:22019+22018+22017+…+2+1的个位数字是5.
(3)29﹣28+27﹣…+23﹣22+2
=28(2﹣1)+26(2﹣1)+24(2﹣1)+22(2﹣1)+2
=28+26+24+22+2
=256+64+16+4+2
=342.
25.(1)由图可知,大长方形的面积等于三个正方形的面积与三个长方形的面积之和,
则,
故答案为:;
(2)由题意得:,
,
∴,
则;
(3)由题意得:,
则,
,
,
,
,
,
即阴影部分的面积为20.
26.(1)由题意得:
(x+2)(3x+1)(5x﹣3)所得多项式的最高次项为x×3x×5x=15x3,
一次项为:1×1×(﹣3)x+2×3×(﹣3)x+2×1×5x=﹣11x,
故答案为:15x3,﹣11x;
(2)依题意有:1×m×(﹣1)+1×(﹣3)×(﹣1)+1×m×2=0,
解得m=﹣3;
(3)根据题意可知即为所得多项式的一次项系数,
∵展开之后x的一次项共有2021个,且每一项的系数都为,
∴
故答案为:2021.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
