北师大版七年级数学下册4.3探索三角形全等的条件一课一练习题2(Word版,含答案)
文档属性
| 名称 | 北师大版七年级数学下册4.3探索三角形全等的条件一课一练习题2(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览

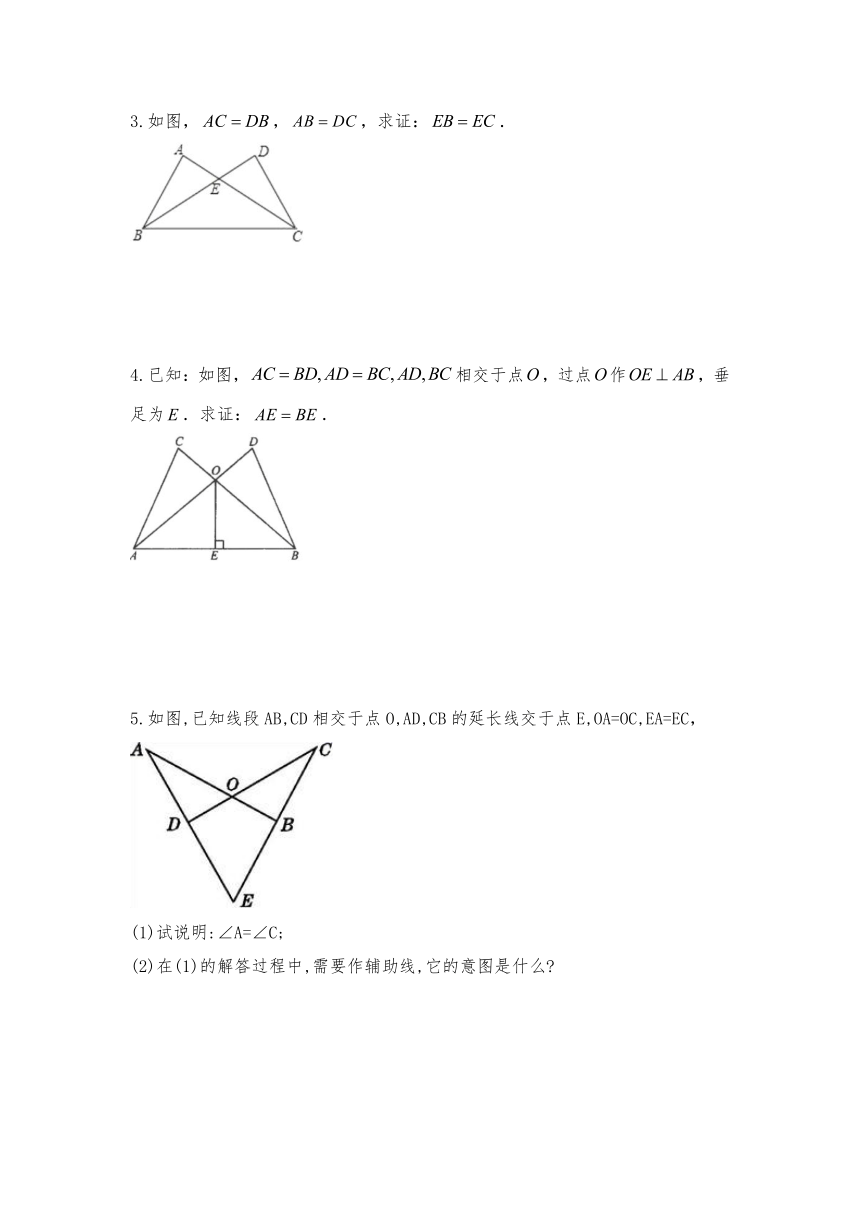
文档简介
4.3《探索三角形全等的条件》习题2
一、选择题
1.如图,,,,则(
)
A.70°
B.45°
C.40°
D.50°
2.下列说法:①全等图形的形状相同、大小相等;②三边对应相等的两个三角形全等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为(
)
A.①②④
B.①③④
C.②③④
D.①②③④
3.如图,已知两个三角形全等,那么∠1的度数是(
)
A.72°;
B.60°;
C.58°;
D.50°.
4.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0)
B.(4,0)
C.(4.﹣2)
D.(4,﹣3)
5.如图,Rt△ABC,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中不正确的是( )
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
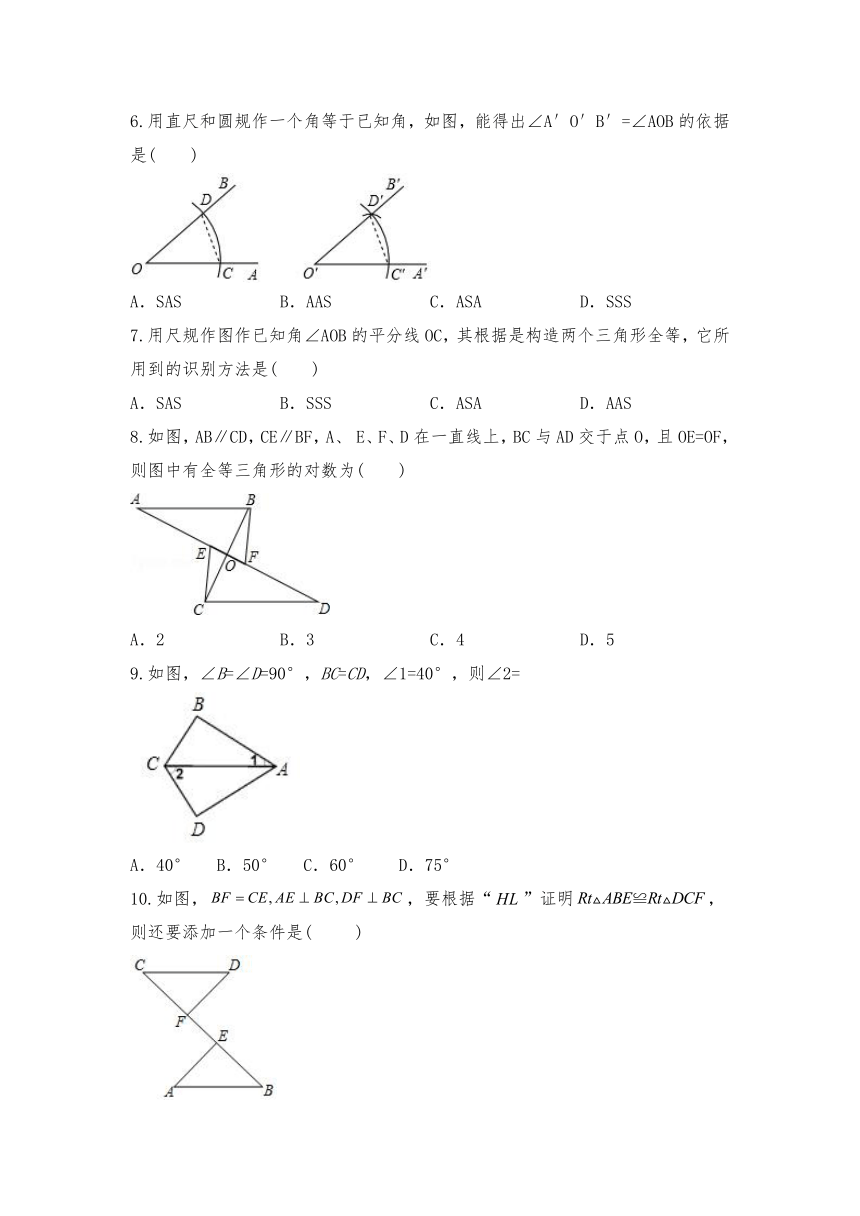
6.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.AAS
C.ASA
D.SSS
7.用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,它所用到的识别方法是(
)
A.SAS
B.SSS
C.ASA
D.AAS
8.如图,AB∥CD,CE∥BF,A、
E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
A.2
B.3
C.4
D.5
9.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
A.40°
B.50°
C.60°
D.75°
10.如图,,要根据“”证明,则还要添加一个条件是(
)
A.
B.
C.
D.
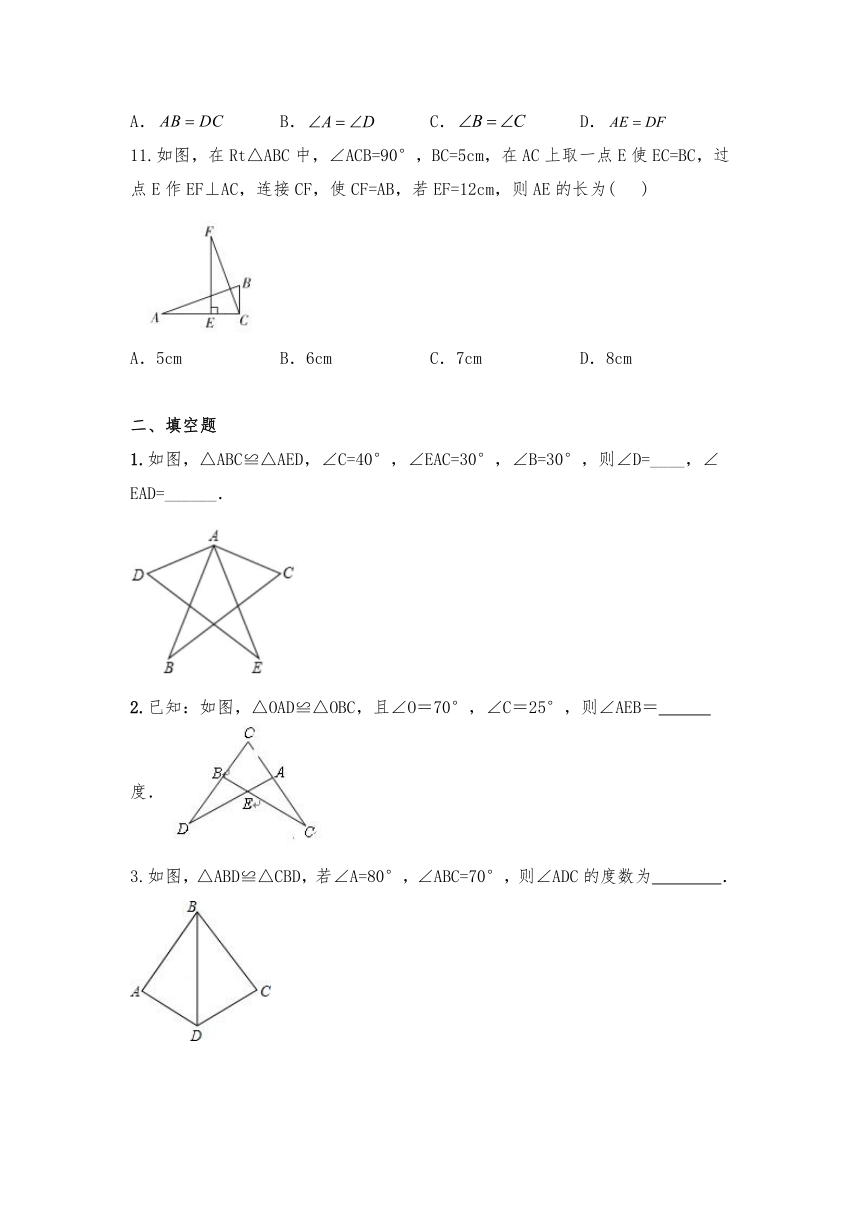
11.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则AE的长为(
)
A.5cm
B.6cm
C.7cm
D.8cm
二、填空题
1.如图,△ABC≌△AED,∠C=40°,∠EAC=30°,∠B=30°,则∠D=____,∠EAD=______.
2.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=
度.
3.如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为
.
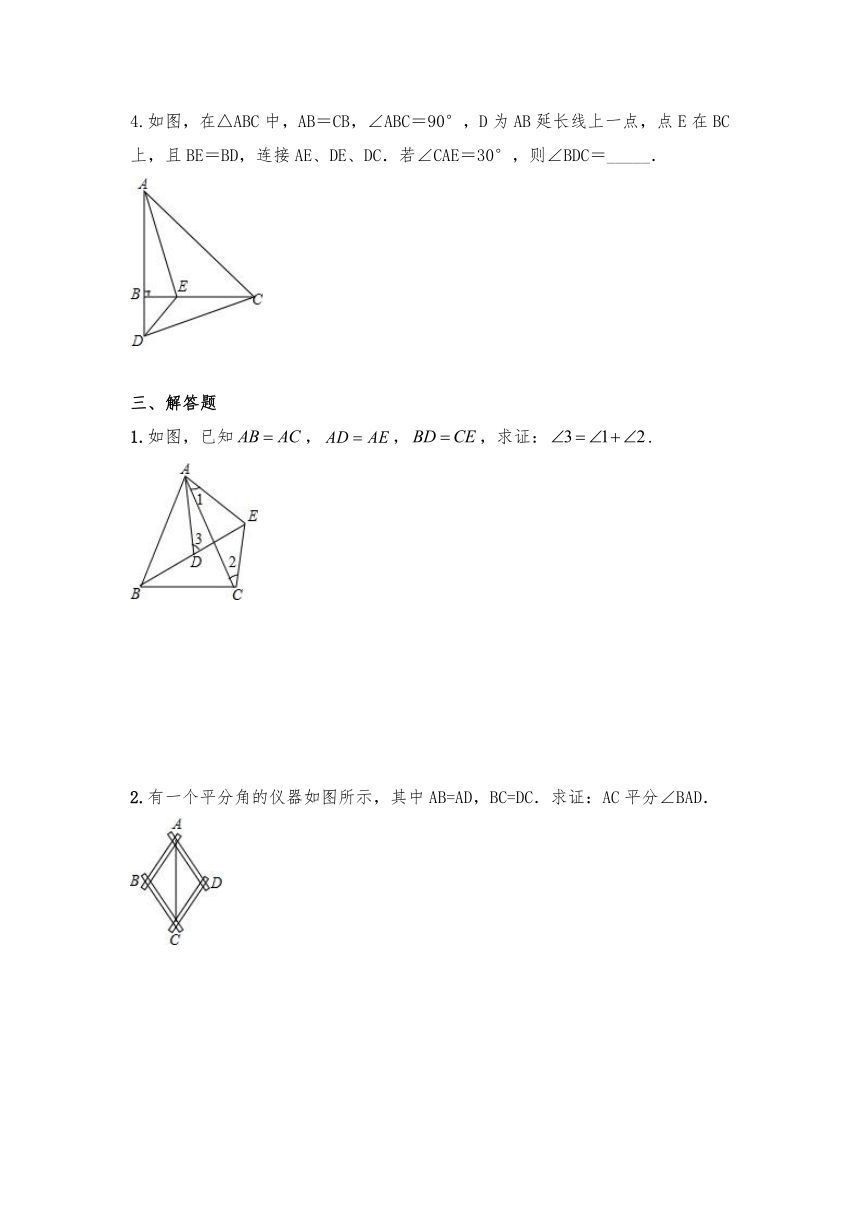
4.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=_____.
三、解答题
1.如图,已知,,,求证:.
2.有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
3.如图,,,求证:.
4.已知:如图,相交于点,过点作,垂足为.求证:.
5.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
6.已知:如图,点A、B、C、D在一条直线上,.
(1)求证:;
(2)若,求的度数.
7.如图,点E、F在BC上,AB=CD,BE=CF,∠B=∠C,AF与DE交于点O.求证:∠A=∠D.
8.如图,,,.,与交于点.
(1)求证:;
(2)求的度数.
9.如图,已知,,.
求证:(1);
(2).
10.如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
11.如图(1),AB=4,AC⊥AB,BD⊥AB,AC=BD=3.点
P
在线段
AB
上以
1的速度由点
A
向点
B
运动,同时,点
Q
在线段
BD
上由点
B
向点
D
运动.它们运动的时间为
(s).
(1)若点
Q
的运动速度与点
P
的运动速度相等,当=1
时,△ACP
与△BPQ
是否全等,请说明理由,
并判断此时线段
PC
和线段
PQ
的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点
Q
的运动速度为,是否存在实数,使得△ACP
与△BPQ
全等?若存在,求出相应的、的值;若不存在,请说明理由.
12.CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠β.
(1)若直线CD经过∠BCA内部,且E、F在射线CD上,
①若∠BCA=90°,∠β=90°,例如左边图,则BE
CF,EF
|BE
-
AF|
(填“>”,“<”,“=”);
②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如中间图,①中的两个结论还成立吗?并说明理由;
(2)如右边图,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).
13.如图,点,,,在同一条直线上,,,.求证:.
14.如图,于点于点,
求证:.
15.如图△ABC中,点E在AB上,连接CE,满足AC=CE,线段CD交AB于F,连接AD.
(1)若∠DAF=∠BCF,∠ACD=∠BCE,求证:AD=BE;
(2)若∠ACD=24°,EF=CF,求∠BAC的度数.
16.如图所示,有两个长度相等的滑梯,左边滑梯BC的高AC与右边滑梯EF水平方向的长度DF相等,两滑梯倾斜角∠ABC和∠DFE有什么关系?并说明理由。
17.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:AB=CD.
18.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
19.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF
;(2)AB∥DE.
答案
一、选择题
1.C.2.D.3.D.4.D.5.B.6.D.7.B.8.B.9.B.10.A.11.C.
二、填空题
1.40°
110°
2.120
3.130°
4.75°
三、解答题
1.在△ABD和△ACE中,
,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
2.证明:在ABC和ADC中,
∴ABC≌ADC(SSS)
∴∠BAC=∠DAC,
∴AC平分∠BAD.
3.证明:在与中,
,
∴;
∴,
∴,
∴.
4.证明:在△ABC与△BAD中,
∴△ABC≌△BAD(SSS),
∴∠ABC=∠BAC,
∴AO=BO,
又∵OE⊥AB,
∴AE=BE.
5.(1)如图,连接OE.
在△EAO和△ECO中,
所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)
在(1)的解答过程中,需要作辅助线,它的意图是构造全等三角形.
6.解:(1)∵AE∥BF,
∴∠A=∠DBF,
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
又∵AE=BF,
∴△ACE≌△BDF(SAS),
∴∠E=∠F;
(2)∵△ACE≌△BDF,
∴∠D=∠ACE=80°,
∵∠A=40°,
∴∠E=180°-∠A-∠ACE=60°.
7.证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS),
∴∠A=∠D.
8.(1)∵,,
∴∠ACB=∠ECD=90°
∴∠ACB+∠BCE=∠ECD+∠BCE
即∠ACE=∠BCD
又.
∴△ACE≌△BCD
∴
(2)∵△ACE≌△BCD
∴∠A=∠B
设AE与BC交于O点,
∴∠AOC=∠BOF
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°
∴∠BFO=∠ACO=90°
故=180°-∠BFO=90°.
9.证明:(1)∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BE-EF=CF-EF,
即BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
10.证明:(1)∵AB∥CD,∴
∠BAG=∠G,
∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G
.
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G,
∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
11.(1)当t=1时,AP=
BQ=1,
BP=
AC=3,
又∠A=∠B=
90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ
,
∴∠APC+∠BPQ=∠APC+∠ACP
=
90
.
∴∠CPQ=
90°,
即线段PC与线段PQ垂直;
(2)①若△ACP≌△BPQ,
则AC=
BP,AP=
BQ,
解得;
②若△ACP≌△BQP,
则AC=
BQ,AP=
BP,
解得:
综上所述,存在或使得△ACP与△BPQ全等.
12.(1)①∵∠BCA=90°,∠β=90°
∴∠FCA+∠BCF=90°,∠FCA+∠CAF=90°
∴∠BCF=∠CAF
又∵∠BEC=∠CFA,CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
∴
②在△FCA中,∠CFA+∠FCA+∠CAF=180°
又∵∠BEC=∠CFA=∠β,∠β+∠BCA=180°
∴∠FCA+∠CAF=∠BCA
∵∠BCA=∠BCE+∠FCA
∴∠CAF=∠BCE
∵CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
∴
(2)在△BEC中,∠B+∠BEC+∠BCE=180°
又∵∠BEC=∠CFA=∠β,∠BCE+∠BCA+∠ACF=180°,∠β=∠BCA
∴∠B=∠ACF
∵CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
EF=EC+CF=AF+BE
13.证明:,
.
又,,
,
.
14.证明:,
,
,
,
在和中,
,
,
,
.
15.解:(1),,
,
又,,
,
;
(2),
,
,
,
又,
中,.
16.解:∠ABC+∠DFE=90°
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF
∴∠ABC=∠DEF
又∵∠DEF+∠DFE=90°
∴∠ABC+∠DFE=90°
17.证明:在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC.
18.证明:(1)∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD平分∠BAC;
(2)AB+AC=2AE.
理由:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
19.解:(1)∵AC⊥BC,DF⊥EF
∴∠ACB=∠DFE=90°
又∵BC=EF
AC=DF
∴△ABC≌△DEF
(2)∵△ABC≌△DEF
∴∠B=∠DEF
∴AB∥DE(同位角相等,两直线平行)
一、选择题
1.如图,,,,则(
)
A.70°
B.45°
C.40°
D.50°
2.下列说法:①全等图形的形状相同、大小相等;②三边对应相等的两个三角形全等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为(
)
A.①②④
B.①③④
C.②③④
D.①②③④
3.如图,已知两个三角形全等,那么∠1的度数是(
)
A.72°;
B.60°;
C.58°;
D.50°.
4.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0)
B.(4,0)
C.(4.﹣2)
D.(4,﹣3)
5.如图,Rt△ABC,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中不正确的是( )
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
6.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.AAS
C.ASA
D.SSS
7.用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,它所用到的识别方法是(
)
A.SAS
B.SSS
C.ASA
D.AAS
8.如图,AB∥CD,CE∥BF,A、
E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
A.2
B.3
C.4
D.5
9.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
A.40°
B.50°
C.60°
D.75°
10.如图,,要根据“”证明,则还要添加一个条件是(
)
A.
B.
C.
D.
11.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则AE的长为(
)
A.5cm
B.6cm
C.7cm
D.8cm
二、填空题
1.如图,△ABC≌△AED,∠C=40°,∠EAC=30°,∠B=30°,则∠D=____,∠EAD=______.
2.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=
度.
3.如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为
.
4.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=_____.
三、解答题
1.如图,已知,,,求证:.
2.有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
3.如图,,,求证:.
4.已知:如图,相交于点,过点作,垂足为.求证:.
5.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
6.已知:如图,点A、B、C、D在一条直线上,.
(1)求证:;
(2)若,求的度数.
7.如图,点E、F在BC上,AB=CD,BE=CF,∠B=∠C,AF与DE交于点O.求证:∠A=∠D.
8.如图,,,.,与交于点.
(1)求证:;
(2)求的度数.
9.如图,已知,,.
求证:(1);
(2).
10.如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
11.如图(1),AB=4,AC⊥AB,BD⊥AB,AC=BD=3.点
P
在线段
AB
上以
1的速度由点
A
向点
B
运动,同时,点
Q
在线段
BD
上由点
B
向点
D
运动.它们运动的时间为
(s).
(1)若点
Q
的运动速度与点
P
的运动速度相等,当=1
时,△ACP
与△BPQ
是否全等,请说明理由,
并判断此时线段
PC
和线段
PQ
的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点
Q
的运动速度为,是否存在实数,使得△ACP
与△BPQ
全等?若存在,求出相应的、的值;若不存在,请说明理由.
12.CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠β.
(1)若直线CD经过∠BCA内部,且E、F在射线CD上,
①若∠BCA=90°,∠β=90°,例如左边图,则BE
CF,EF
|BE
-
AF|
(填“>”,“<”,“=”);
②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如中间图,①中的两个结论还成立吗?并说明理由;
(2)如右边图,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).
13.如图,点,,,在同一条直线上,,,.求证:.
14.如图,于点于点,
求证:.
15.如图△ABC中,点E在AB上,连接CE,满足AC=CE,线段CD交AB于F,连接AD.
(1)若∠DAF=∠BCF,∠ACD=∠BCE,求证:AD=BE;
(2)若∠ACD=24°,EF=CF,求∠BAC的度数.
16.如图所示,有两个长度相等的滑梯,左边滑梯BC的高AC与右边滑梯EF水平方向的长度DF相等,两滑梯倾斜角∠ABC和∠DFE有什么关系?并说明理由。
17.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:AB=CD.
18.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
19.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF
;(2)AB∥DE.
答案
一、选择题
1.C.2.D.3.D.4.D.5.B.6.D.7.B.8.B.9.B.10.A.11.C.
二、填空题
1.40°
110°
2.120
3.130°
4.75°
三、解答题
1.在△ABD和△ACE中,
,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
2.证明:在ABC和ADC中,
∴ABC≌ADC(SSS)
∴∠BAC=∠DAC,
∴AC平分∠BAD.
3.证明:在与中,
,
∴;
∴,
∴,
∴.
4.证明:在△ABC与△BAD中,
∴△ABC≌△BAD(SSS),
∴∠ABC=∠BAC,
∴AO=BO,
又∵OE⊥AB,
∴AE=BE.
5.(1)如图,连接OE.
在△EAO和△ECO中,
所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)
在(1)的解答过程中,需要作辅助线,它的意图是构造全等三角形.
6.解:(1)∵AE∥BF,
∴∠A=∠DBF,
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
又∵AE=BF,
∴△ACE≌△BDF(SAS),
∴∠E=∠F;
(2)∵△ACE≌△BDF,
∴∠D=∠ACE=80°,
∵∠A=40°,
∴∠E=180°-∠A-∠ACE=60°.
7.证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS),
∴∠A=∠D.
8.(1)∵,,
∴∠ACB=∠ECD=90°
∴∠ACB+∠BCE=∠ECD+∠BCE
即∠ACE=∠BCD
又.
∴△ACE≌△BCD
∴
(2)∵△ACE≌△BCD
∴∠A=∠B
设AE与BC交于O点,
∴∠AOC=∠BOF
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°
∴∠BFO=∠ACO=90°
故=180°-∠BFO=90°.
9.证明:(1)∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BE-EF=CF-EF,
即BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
10.证明:(1)∵AB∥CD,∴
∠BAG=∠G,
∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G
.
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G,
∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
11.(1)当t=1时,AP=
BQ=1,
BP=
AC=3,
又∠A=∠B=
90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ
,
∴∠APC+∠BPQ=∠APC+∠ACP
=
90
.
∴∠CPQ=
90°,
即线段PC与线段PQ垂直;
(2)①若△ACP≌△BPQ,
则AC=
BP,AP=
BQ,
解得;
②若△ACP≌△BQP,
则AC=
BQ,AP=
BP,
解得:
综上所述,存在或使得△ACP与△BPQ全等.
12.(1)①∵∠BCA=90°,∠β=90°
∴∠FCA+∠BCF=90°,∠FCA+∠CAF=90°
∴∠BCF=∠CAF
又∵∠BEC=∠CFA,CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
∴
②在△FCA中,∠CFA+∠FCA+∠CAF=180°
又∵∠BEC=∠CFA=∠β,∠β+∠BCA=180°
∴∠FCA+∠CAF=∠BCA
∵∠BCA=∠BCE+∠FCA
∴∠CAF=∠BCE
∵CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
∴
(2)在△BEC中,∠B+∠BEC+∠BCE=180°
又∵∠BEC=∠CFA=∠β,∠BCE+∠BCA+∠ACF=180°,∠β=∠BCA
∴∠B=∠ACF
∵CA=CB
∴△BEC△CFA(AAS)
∴BE=CF,CE=AF
EF=EC+CF=AF+BE
13.证明:,
.
又,,
,
.
14.证明:,
,
,
,
在和中,
,
,
,
.
15.解:(1),,
,
又,,
,
;
(2),
,
,
,
又,
中,.
16.解:∠ABC+∠DFE=90°
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF
∴∠ABC=∠DEF
又∵∠DEF+∠DFE=90°
∴∠ABC+∠DFE=90°
17.证明:在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC.
18.证明:(1)∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD平分∠BAC;
(2)AB+AC=2AE.
理由:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
19.解:(1)∵AC⊥BC,DF⊥EF
∴∠ACB=∠DFE=90°
又∵BC=EF
AC=DF
∴△ABC≌△DEF
(2)∵△ABC≌△DEF
∴∠B=∠DEF
∴AB∥DE(同位角相等,两直线平行)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
