北师大版七年级数学下册4.1认识三角形一课一练习题1(Word版,含答案)
文档属性
| 名称 | 北师大版七年级数学下册4.1认识三角形一课一练习题1(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 502.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:10:58 | ||
图片预览


文档简介
4.1《认识三角形》习题1
一、选择题
1.学习完三角形的概念后,小强同学用火柴拼成的图形如下,其中符合三角形概念的是(
)
A.
B.
C.
D.
2.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法:
①三角形有且只有一条中线;②三角形的高一定在三角形内部;③三角形的两边之差大于第三边;④三角形按边分类可分为等腰三角形和不等边三角形.其中错误的说法是(
)
A.①②
B.①③
C.①②③
D.①②③④
3.若一个三角形的三个内角的度数之比为,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.下列说法错误的是(
)
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
5.如图,王师傅用六根木条钉成一个六边形木框,要使它不变形,至少还要再钉上________根木条(
)
A.2
B.3
C.4
D.5
6.如图,分别是的中线与角平分线,若,则的度数是(
)
A.
B.
C.
D.
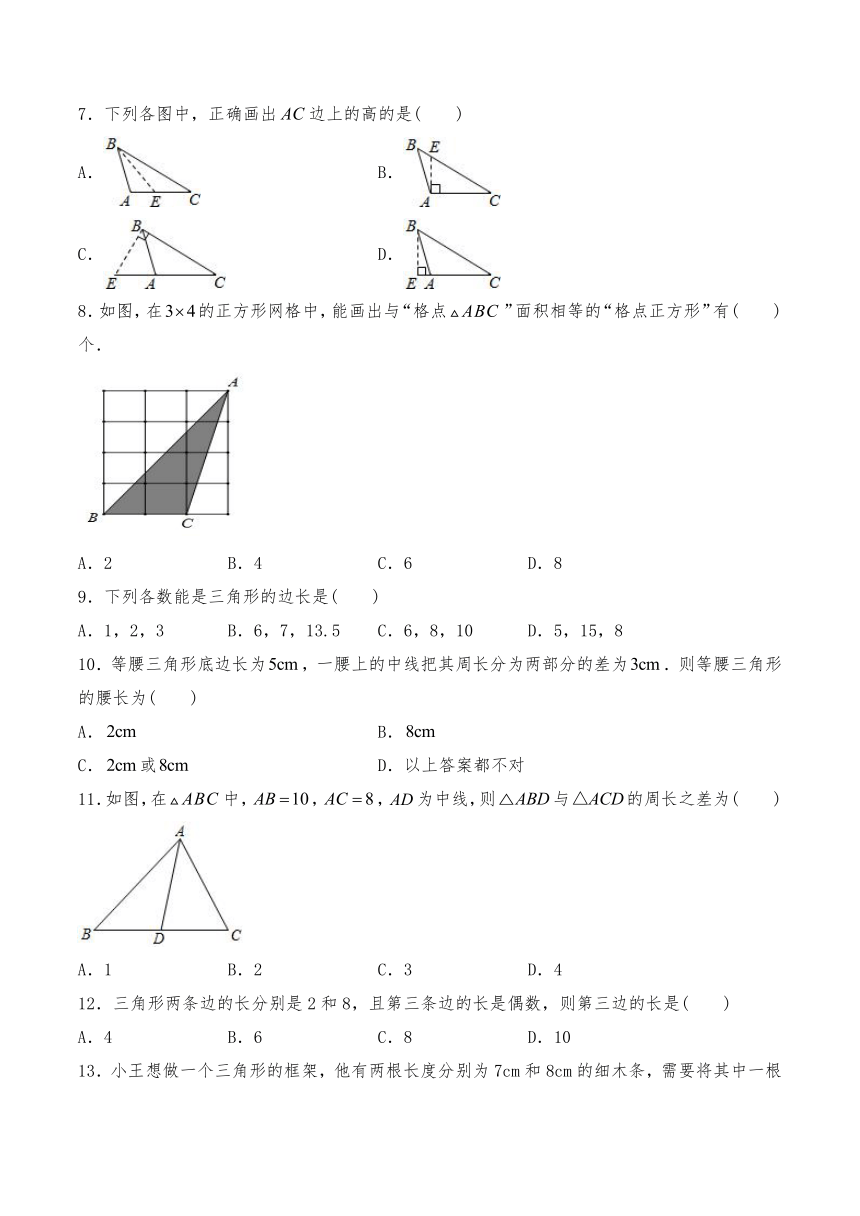
7.下列各图中,正确画出边上的高的是(
)
A.
B.
C.
D.
8.如图,在的正方形网格中,能画出与“格点”面积相等的“格点正方形”有(
)个.
A.2
B.4
C.6
D.8
9.下列各数能是三角形的边长是(
)
A.1,2,3
B.6,7,13.5
C.6,8,10
D.5,15,8
10.等腰三角形底边长为,一腰上的中线把其周长分为两部分的差为.则等腰三角形的腰长为(
)
A.
B.
C.或
D.以上答案都不对
11.如图,在中,,,为中线,则与的周长之差为(
)
A.1
B.2
C.3
D.4
12.三角形两条边的长分别是2和8,且第三条边的长是偶数,则第三边的长是( )
A.4
B.6
C.8
D.10
13.小王想做一个三角形的框架,他有两根长度分别为7cm和8cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么可以分为两截的木条是(
)
A.7cm的木条
B.8cm的木条
C.两根都可以
D.两根都不行
14.如图所示,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=16cm2,则阴影部分(△BEF)的面积等于( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
二、填空题
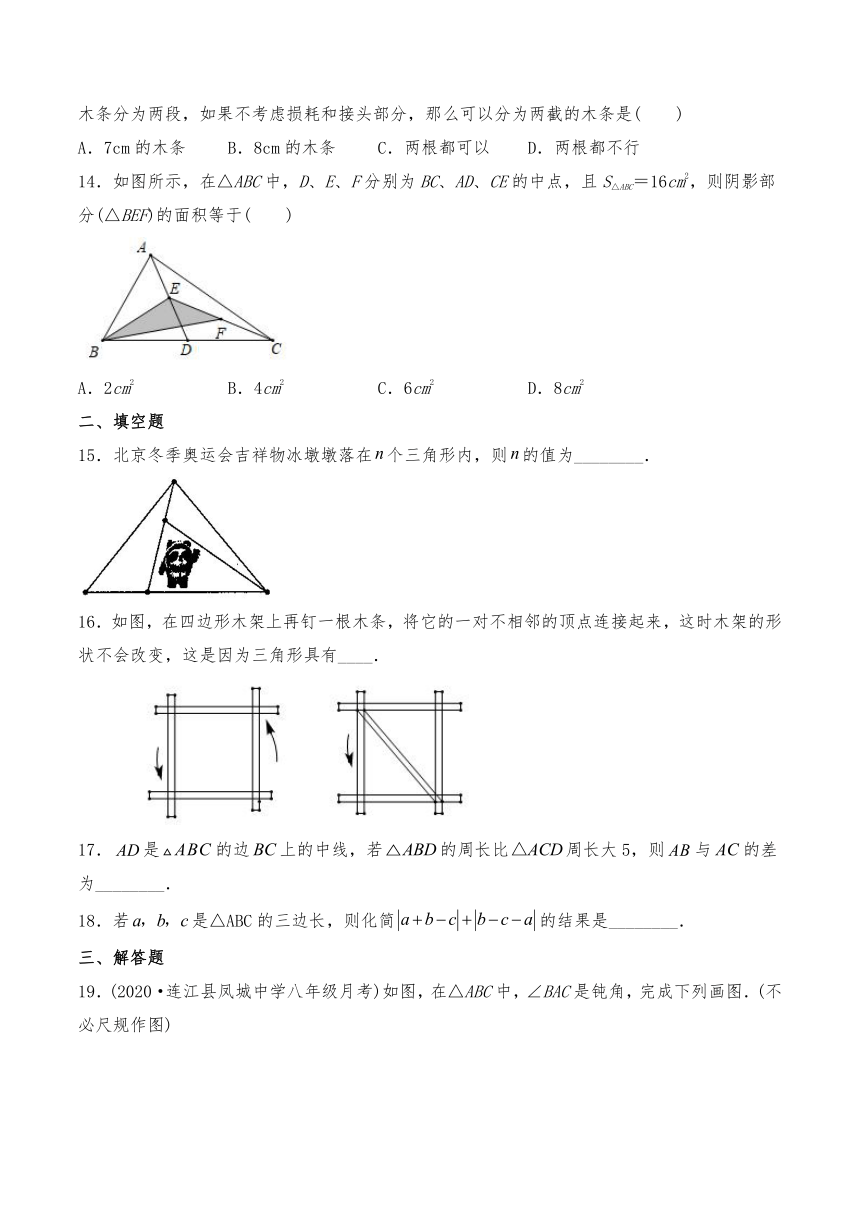
15.北京冬季奥运会吉祥物冰墩墩落在个三角形内,则的值为________.
16.如图,在四边形木架上再钉一根木条,将它的一对不相邻的顶点连接起来,这时木架的形状不会改变,这是因为三角形具有____.
17.是的边上的中线,若的周长比周长大5,则与的差为________.
18.若是△ABC的三边长,则化简的结果是________.
三、解答题
19.(2020·连江县凤城中学八年级月考)如图,在△ABC中,∠BAC是钝角,完成下列画图.(不必尺规作图)
(1)∠BAC的平分线AD;
(2)AC边上的中线BE;
(3)AC边上的高BF.
20.已知,的三边长为,,.
(1)求的周长的取值范围;
(2)当的周长为偶数时,求.
21.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
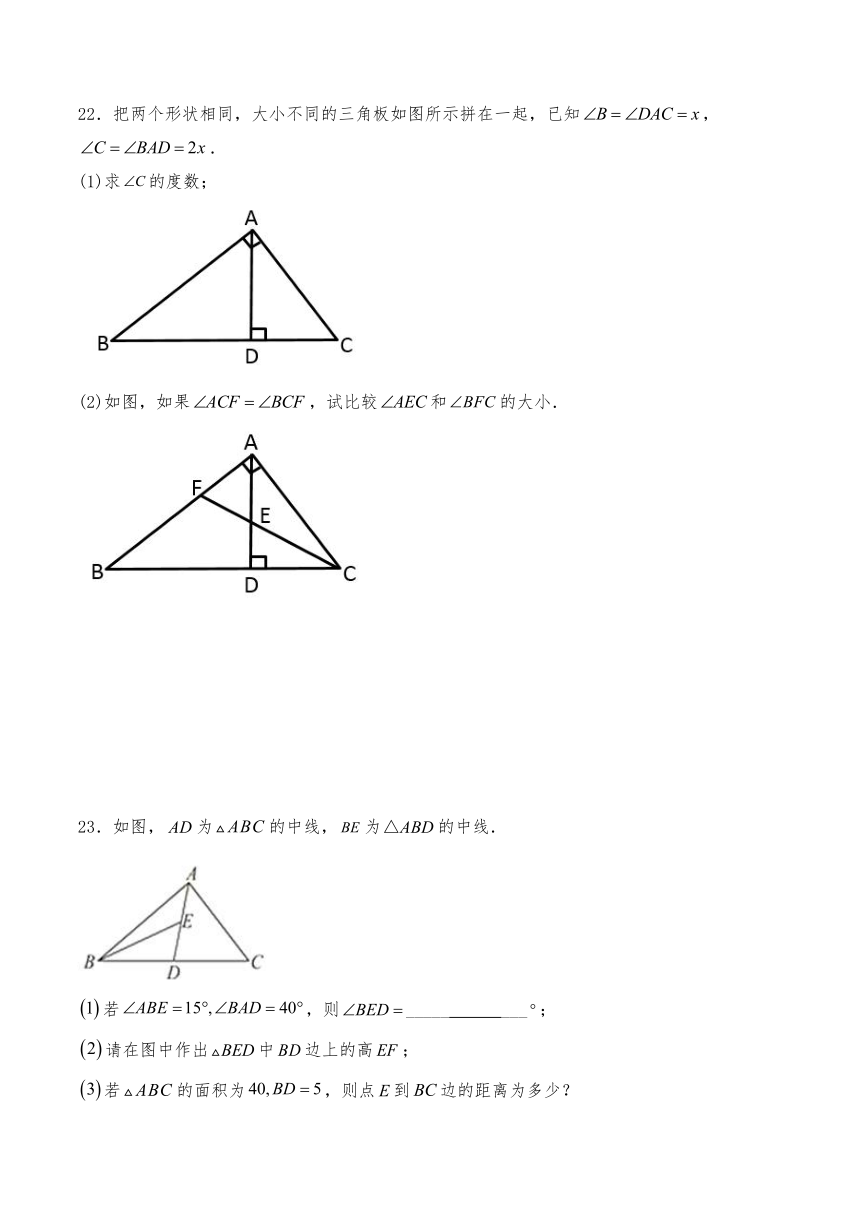
22.把两个形状相同,大小不同的三角板如图所示拼在一起,已知,.
(1)求的度数;
(2)如图,如果,试比较和的大小.
23.如图,为的中线,为的中线.
若,则_____
___;
请在图中作出中边上的高;
若的面积为,则点到边的距离为多少?
24.阅读材料:若,求,的值.
解:∵,∴,
∴,∴,,∴,.
根据你的观察,探究下面的问题:
(1)已知,则________,________;
(2)已知的三边长、、都是正整数,且满足,求的周长.
25.题情景:在三角形纸片内部给定-些点,满足这些点连同三角形三个顶点没有三个点在一条直线上,以这些点为顶点,将纸片剪成-些小三角形纸片,一共能得到几个小三角形?
问题解决:甲同学绘制了如下三个图,分别在三角形内部取1个点、2个点,如下图所示:
继续探究:在三角形内部取三个点,画出分割的图形,并经过观察计数完成表格:
内部点的个数
1
2
3
n
得到三角形个数
3
5
拓展联系:当纸片是四边形时,探究此时内部所取点的个数与得到三角心个数的关系,完成表格:
内部点的个数
1
2
3
n
得到三角形个数
概括提升:设纸片的边数为m,内部点的个数为n,得到三角形的个数是x,请直接写出x与m、n的关系:______________.
26.如图,在中,,是的角平分线,,垂足为,延长与外角的平分线交于点.
(1)若,求和的度数;
(2)若,请直接写出和的度数(用含的代数式表示);
(3)若高和的角平分线交于点,在(2)的条件下求的度数(用含的代数式表示).
答案
一、选择题
1.C.2.C.3.B.4.A.5.B6.B.7.D.8.C.9.C.10.B.
11.B.12.C.13.B.14.B
二、填空题
15..
16.稳定性.
17.5.
18.2a.
三、解答题
19.
解:(1)如图所示:AD即为所求;
(2)如图所示:BE即为所求;
(3)如图所示:BF即为所求.
20.
解:(1)的三边长分别为,,,
,即,
的周长,
即:的周长;
(2)的周长是偶数,由(1)结果得的周长可以是,或,
的值为,或.
21.解:(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16∴不能构成三角形,故不能求出DC的长.
22.解:(1)由图可知:
∠BAC=90°,即∠BAD+∠DAC=90°,
∵∠B=∠DAC=x,∠C=∠BAD=2x,
∴2x+x=90°,
∴x=30°,
∴∠C=60°;
(2)由图可知:∠BAC=∠ADC=90°,
∵∠AEC=∠ADC+∠BCF=∠90°+∠BCF,∠BFC=∠BAC+∠ACF=90°+∠ACF,
且∠ACF=∠BCF,
∴∠AEC=∠BFC.
23.
在△ABE中,
∵∠ABE=15°,∠BAD=40°,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
故答案为;
如图所示:
∵AD为△ABC的中线,BE为△ABD的中线
∴
∴
∵△ABC的面积为40,BD=5,
∴
∴
24.解:(1)由得
,
,
∴,,
∴,
故答案为:-4,-4;
(2)由得:
,
,
∴a-1=0,b-4=0,
∴a=1,b=4,
∴3<c<5,
∵△ABC的三边长a、b、c都是正整数,
∴c=4,
∴的周长为9.
25.
解:继续探究:如图,
在三角形纸片内部给定1个点,得到3个三角形;
在三角形纸片内部给定2个点,得到5个三角形;
在三角形纸片内部给定3个点,得到7个三角形;
在三角形纸片内部给定n个点,得到(2n+1)个三角形;
故填表得:
内部点的个数
1
2
3
n
得到三角形个数
3
5
7
2n+1
拓展联系:如图:
在四边形纸片内部给定1个点,得到4个三角形;
在四边形纸片内部给定2个点,得到6个三角形;
在四边形纸片内部给定3个点,得到8个三角形;
在四边形纸片内部给定n个点,得到(2n+2)个三角形;
填表如下:
内部点的个数
1
2
3
n
得到三角形个数
4
6
8
(2n+2)
概括提升:
(3)设纸片的边数为m,内部给定1个点,得到m个三角
形,
内部给定2个点,得到(m+2)个三角形,
内部给定3个点,得到(m+2×2)个三角形,
内部给定n个点,得到(2n+m-2)个三角形,
∴x=2n+n-2.
26.解:(1)∵CD⊥AB,∠A=60°,
∴∠ADC=90°,∠ACD=30°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE-∠ACD=45°-30°=15°,
∵∠ABG=∠A+∠ACB=150°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=75°,
∵∠FBG=∠F+∠FCB,
∴∠F=75°-45°=30°.
(2)∵CD⊥AB,∠A=n°,
∴∠ADC=90°,∠ACD=90°-n°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE-∠ACD=45°-90°+n°=n°-45°,
∵∠ABG=∠A+∠ACB=90°+n°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=45°+n°
∵∠FBG=∠F+∠FCB,
∴∠F=n°.
(3)如图,过作于,作的角平分线交于
∵FH⊥CG,
∴∠FHC=90°,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB=n°,
∵CQ平分∠DCB,
∴∠QCH=n°,
∴∠CQH=90°-n°.
一、选择题
1.学习完三角形的概念后,小强同学用火柴拼成的图形如下,其中符合三角形概念的是(
)
A.
B.
C.
D.
2.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法:
①三角形有且只有一条中线;②三角形的高一定在三角形内部;③三角形的两边之差大于第三边;④三角形按边分类可分为等腰三角形和不等边三角形.其中错误的说法是(
)
A.①②
B.①③
C.①②③
D.①②③④
3.若一个三角形的三个内角的度数之比为,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.下列说法错误的是(
)
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
5.如图,王师傅用六根木条钉成一个六边形木框,要使它不变形,至少还要再钉上________根木条(
)
A.2
B.3
C.4
D.5
6.如图,分别是的中线与角平分线,若,则的度数是(
)
A.
B.
C.
D.
7.下列各图中,正确画出边上的高的是(
)
A.
B.
C.
D.
8.如图,在的正方形网格中,能画出与“格点”面积相等的“格点正方形”有(
)个.
A.2
B.4
C.6
D.8
9.下列各数能是三角形的边长是(
)
A.1,2,3
B.6,7,13.5
C.6,8,10
D.5,15,8
10.等腰三角形底边长为,一腰上的中线把其周长分为两部分的差为.则等腰三角形的腰长为(
)
A.
B.
C.或
D.以上答案都不对
11.如图,在中,,,为中线,则与的周长之差为(
)
A.1
B.2
C.3
D.4
12.三角形两条边的长分别是2和8,且第三条边的长是偶数,则第三边的长是( )
A.4
B.6
C.8
D.10
13.小王想做一个三角形的框架,他有两根长度分别为7cm和8cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么可以分为两截的木条是(
)
A.7cm的木条
B.8cm的木条
C.两根都可以
D.两根都不行
14.如图所示,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=16cm2,则阴影部分(△BEF)的面积等于( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
二、填空题
15.北京冬季奥运会吉祥物冰墩墩落在个三角形内,则的值为________.
16.如图,在四边形木架上再钉一根木条,将它的一对不相邻的顶点连接起来,这时木架的形状不会改变,这是因为三角形具有____.
17.是的边上的中线,若的周长比周长大5,则与的差为________.
18.若是△ABC的三边长,则化简的结果是________.
三、解答题
19.(2020·连江县凤城中学八年级月考)如图,在△ABC中,∠BAC是钝角,完成下列画图.(不必尺规作图)
(1)∠BAC的平分线AD;
(2)AC边上的中线BE;
(3)AC边上的高BF.
20.已知,的三边长为,,.
(1)求的周长的取值范围;
(2)当的周长为偶数时,求.
21.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
22.把两个形状相同,大小不同的三角板如图所示拼在一起,已知,.
(1)求的度数;
(2)如图,如果,试比较和的大小.
23.如图,为的中线,为的中线.
若,则_____
___;
请在图中作出中边上的高;
若的面积为,则点到边的距离为多少?
24.阅读材料:若,求,的值.
解:∵,∴,
∴,∴,,∴,.
根据你的观察,探究下面的问题:
(1)已知,则________,________;
(2)已知的三边长、、都是正整数,且满足,求的周长.
25.题情景:在三角形纸片内部给定-些点,满足这些点连同三角形三个顶点没有三个点在一条直线上,以这些点为顶点,将纸片剪成-些小三角形纸片,一共能得到几个小三角形?
问题解决:甲同学绘制了如下三个图,分别在三角形内部取1个点、2个点,如下图所示:
继续探究:在三角形内部取三个点,画出分割的图形,并经过观察计数完成表格:
内部点的个数
1
2
3
n
得到三角形个数
3
5
拓展联系:当纸片是四边形时,探究此时内部所取点的个数与得到三角心个数的关系,完成表格:
内部点的个数
1
2
3
n
得到三角形个数
概括提升:设纸片的边数为m,内部点的个数为n,得到三角形的个数是x,请直接写出x与m、n的关系:______________.
26.如图,在中,,是的角平分线,,垂足为,延长与外角的平分线交于点.
(1)若,求和的度数;
(2)若,请直接写出和的度数(用含的代数式表示);
(3)若高和的角平分线交于点,在(2)的条件下求的度数(用含的代数式表示).
答案
一、选择题
1.C.2.C.3.B.4.A.5.B6.B.7.D.8.C.9.C.10.B.
11.B.12.C.13.B.14.B
二、填空题
15..
16.稳定性.
17.5.
18.2a.
三、解答题
19.
解:(1)如图所示:AD即为所求;
(2)如图所示:BE即为所求;
(3)如图所示:BF即为所求.
20.
解:(1)的三边长分别为,,,
,即,
的周长,
即:的周长;
(2)的周长是偶数,由(1)结果得的周长可以是,或,
的值为,或.
21.解:(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16
22.解:(1)由图可知:
∠BAC=90°,即∠BAD+∠DAC=90°,
∵∠B=∠DAC=x,∠C=∠BAD=2x,
∴2x+x=90°,
∴x=30°,
∴∠C=60°;
(2)由图可知:∠BAC=∠ADC=90°,
∵∠AEC=∠ADC+∠BCF=∠90°+∠BCF,∠BFC=∠BAC+∠ACF=90°+∠ACF,
且∠ACF=∠BCF,
∴∠AEC=∠BFC.
23.
在△ABE中,
∵∠ABE=15°,∠BAD=40°,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
故答案为;
如图所示:
∵AD为△ABC的中线,BE为△ABD的中线
∴
∴
∵△ABC的面积为40,BD=5,
∴
∴
24.解:(1)由得
,
,
∴,,
∴,
故答案为:-4,-4;
(2)由得:
,
,
∴a-1=0,b-4=0,
∴a=1,b=4,
∴3<c<5,
∵△ABC的三边长a、b、c都是正整数,
∴c=4,
∴的周长为9.
25.
解:继续探究:如图,
在三角形纸片内部给定1个点,得到3个三角形;
在三角形纸片内部给定2个点,得到5个三角形;
在三角形纸片内部给定3个点,得到7个三角形;
在三角形纸片内部给定n个点,得到(2n+1)个三角形;
故填表得:
内部点的个数
1
2
3
n
得到三角形个数
3
5
7
2n+1
拓展联系:如图:
在四边形纸片内部给定1个点,得到4个三角形;
在四边形纸片内部给定2个点,得到6个三角形;
在四边形纸片内部给定3个点,得到8个三角形;
在四边形纸片内部给定n个点,得到(2n+2)个三角形;
填表如下:
内部点的个数
1
2
3
n
得到三角形个数
4
6
8
(2n+2)
概括提升:
(3)设纸片的边数为m,内部给定1个点,得到m个三角
形,
内部给定2个点,得到(m+2)个三角形,
内部给定3个点,得到(m+2×2)个三角形,
内部给定n个点,得到(2n+m-2)个三角形,
∴x=2n+n-2.
26.解:(1)∵CD⊥AB,∠A=60°,
∴∠ADC=90°,∠ACD=30°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE-∠ACD=45°-30°=15°,
∵∠ABG=∠A+∠ACB=150°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=75°,
∵∠FBG=∠F+∠FCB,
∴∠F=75°-45°=30°.
(2)∵CD⊥AB,∠A=n°,
∴∠ADC=90°,∠ACD=90°-n°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE-∠ACD=45°-90°+n°=n°-45°,
∵∠ABG=∠A+∠ACB=90°+n°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=45°+n°
∵∠FBG=∠F+∠FCB,
∴∠F=n°.
(3)如图,过作于,作的角平分线交于
∵FH⊥CG,
∴∠FHC=90°,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB=n°,
∵CQ平分∠DCB,
∴∠QCH=n°,
∴∠CQH=90°-n°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
